什么是卷积？在数字信号处理里面怎么用的呢？

给出差分方程画个图吧。比如差分方程为y(n)=x(n)+5x(n-1)-4x(n-2)，画出该系统的横截型结构图。什么是横截型结构啊？这个时候还不知道，那就麻烦了，赶快到书中找这个知识点。这是最基础的。再想想如何表达延时？有了这些概念，结构图就能画出来了。画出结构图，那么系统的功能就浮出了水面。

很多人到了大学就丢失了高中时期学习的习惯。在课上，你会发现没有带书带本子的学生，就在那干坐着。我看了都觉得是在浪费时间。他是被逼着来的。但他的班主任能一直逼他学习吗？那么多学生呢？不说了，该讲什么知识就说什么知识吧。课后复习的情况几乎没有。这是我接触到的现象，头大啊！

接着上堂课回顾一下FFT的知识。比如能够画出长度N=4，采用基-2时间抽选法的FFT流图吗？回想一下上一堂课讲的那张图，请对照着画一遍。

卷积！！！

在泛函分析中，卷积、旋积或摺积(英语：Convolution)是通过两个函数f 和g 生成第三个函数的一种数学算子，表征函数f 与g经过翻转和平移的重叠部分的面积。如果将参加卷积的一个函数看作区间的指示函数，卷积还可以被看作是“滑动平均”的推广。那么在数字信号处理里面怎么用的呢？考试必考！！！估计同学们早已经忘了。

卷积的概念？

这个过程一定要牢记！！！给出知识总结的内容，希望同学们认真学习，从而真正的掌握！大学学习不仅要学理论，还要锻炼思维！

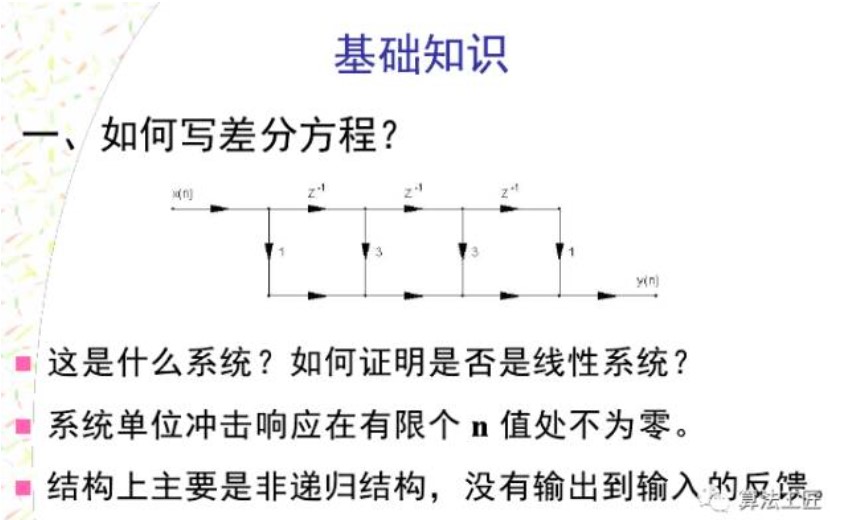
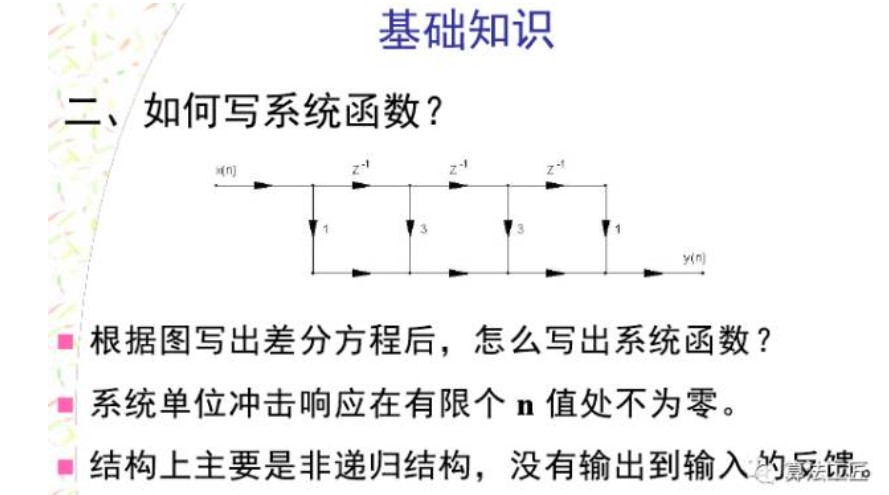
用单位脉冲响应h(n)可以表示线性时不变离散系统，这时 y（n）=x（n）*h（n）两边取z变换：Y(z)=X(z)H(z)则定义为系统函数。

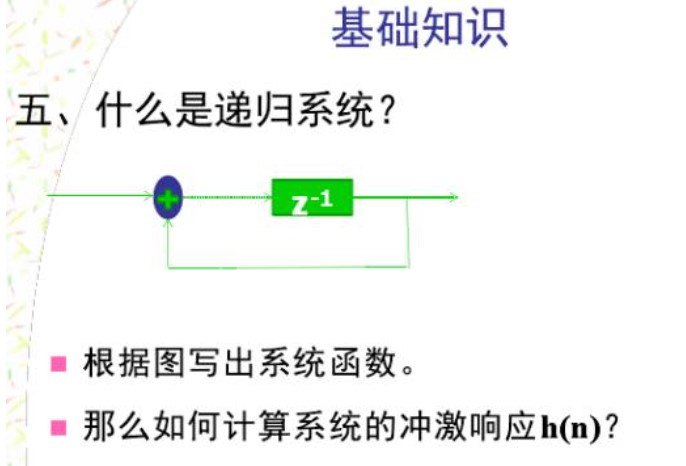
再次强调：用单位脉冲响应h(n)可以表示线性时不变离散系统，这时 y（n）=x（n）*h（n）两边取z变换：Y(z)=X(z)H(z)则定义为系统函数。它是单位脉冲响应的z变换。单位圆上的系统函数z=e就是系统的频率响应。所以可以用单位脉冲响应的z变换来描述线性时不变离散系统。百度百科写的很棒！

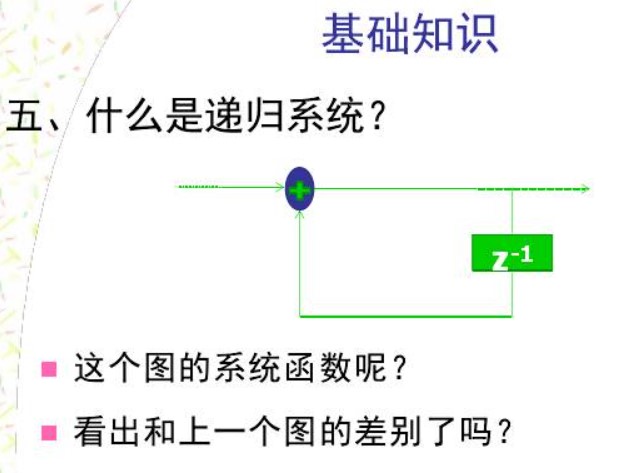
只有扎扎实实的做完这些题目，才能掌握数字信号处理的核心内容。未完，待续！

审核编辑：刘清