在计算光学领域,平生不把“相位”玩,便称英雄也枉然!相位,是计算光学成像里绕不开的东西,号称“凌波微步”的相位大法,是计算光学成像的十八般武艺之一。
今天,我们就来揭开相位的神秘面纱。
平静的水面扔进一颗石子,会荡起一圈圈的涟漪;燃烧的火堆后面,能看到影影绰绰变形了的脸;一束激光照射到全息干板上,能看到栩栩如生的三维立体图像;滴答走着的钟表,地上被老大爷抽打着转了一圈又一圈的陀螺……所有这些,都与 “相位”有关。
可是,说起相位(Phase),大家似乎都感觉到熟悉又陌生。这个词不仅在计算光学成像中随处可见,而且在光学、数学和信号处理领域也司空见惯,但好像每次见到都感觉有些不同。我见过很多光学专业的学生会有一个思维定势,认为相位应该是光波函数的相位,而当他们阅读一些文献的时候,见到相位往往就莫衷一是的样子,手足无措。
那么计算成像里的相位都有哪些?相位能带来什么?我们还能对相位做点什么?如何在计算成像中引入相位和解译相位?
1
相位到底是什么?
我们生活在一个充满各种各样波的世界里,要理解相位,首先得了解什么是波。有些人可能觉得这个问题有些奇怪,这还用问吗?划船时的水波,广播里的声波,跳绳时的绳波。当然,生活中的还存在着很多波动现象。我们要透过现象看本质,就是我们如何用一套统一的数学语言来描述波。
光是一种电磁波,它满足波动方程:
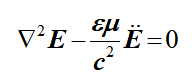
求解这个方程不是我们在此处需要深入探讨的问题,感兴趣的读者可以移步光学大师波恩老先生的著作《光学原理》。
我们先来看看相位的定义,以简谐波为例,若一个正弦函数y=A·sin(ωt+α)描述了角频率为ω、振幅为A的一个振动,其中ωt+α就是相位。
如果写成y(x,t)=A·sin(ωt+α-kx)的形式,就描述了一个振幅为A、波长为λ=2π/k的波。换句话说,相位是描述“振荡”的,存在于周期性现象的描述中,类似于振动、交流电、波动等等。 是不是很枯燥?那就来看个更枯燥的。在物理和应用科学中,经常用复函数Y(x,t)=C·ei(ωt-kx),其中复振幅C=Aeiα·Y(x,t)的虚部对应上面的那个y(x,t)。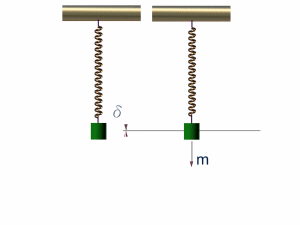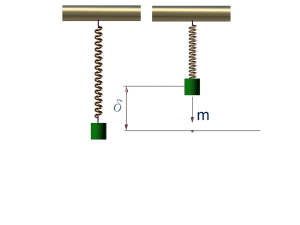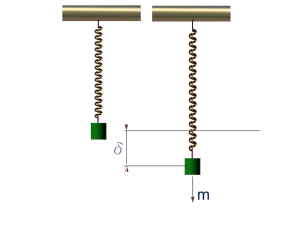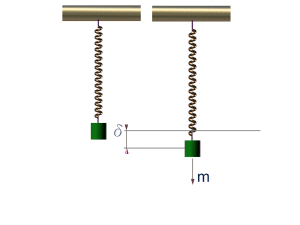
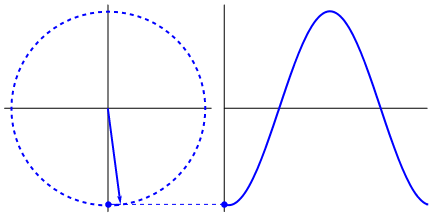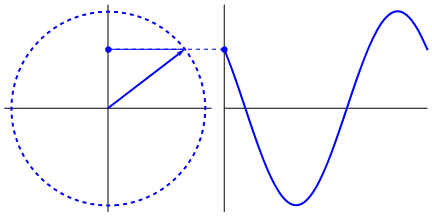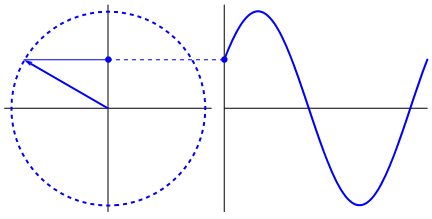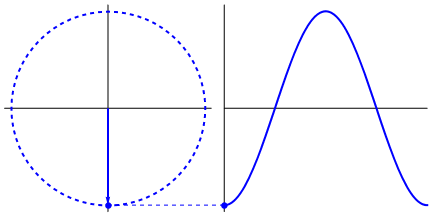
简谐运动的相位与波的相位
之所以讲这些枯燥的内容,只是想把来龙去脉搞清楚。 这里需要总结一下:所有写成复数形式的式子都有相位,而相位是与幅角相关的一个相对值。
你看,这不就简单了吗?再强调一下:凡是复数形式的,必有相位;相位是一个相对值,一定要与初始位置一起用。
其实,还可以归纳一条:凡是能够表示成周期性函数的,都有相位。 打个比方,排列整齐的队伍在一声“解散”口令后,立马就成杂乱无序状;一声“归位”令下,很快就又恢复了排列整齐的队伍。
在这里,每个人都有自己的位置,这个位置就相当于相位。
队列归位 因此,你会看到五花八门的各种复数表达式,很显然,这些复数表达式里都有相位,只是,你可能不知道这个相位到底表达什么意思。
那我们就来列举一下计算光学成像中会遇到哪些相位。 第一是大家熟悉的光波函数,有幅值有相位。由于光的探测是强度信息,相位探测都是间接方法测量出来,比如干涉法。自然光的时间相干性和空间相干性都很差,可以认为相位杂乱无章,变化无常,难以记录。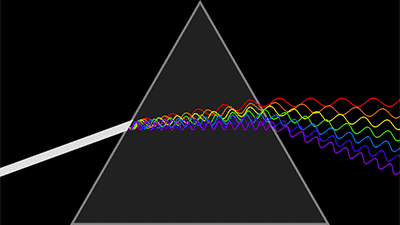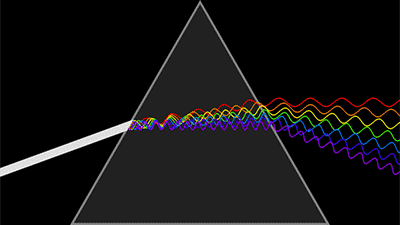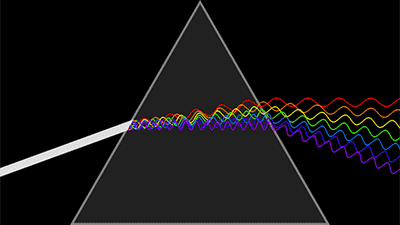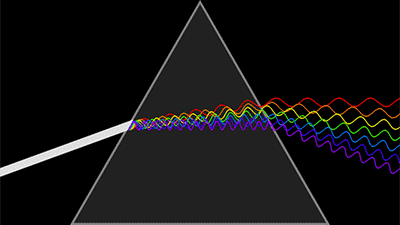
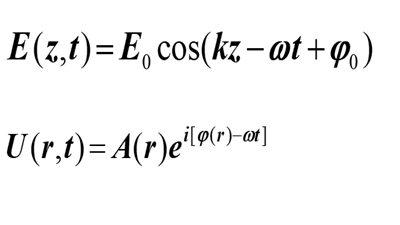
光波与波函数 第二是全息,我们知道全息表示形式本身就是复数的,自然有相位;最重要的是,全息记录的就是相位信息,只需用满足布拉格条件的再现光照射全息图就能重建出原始相位。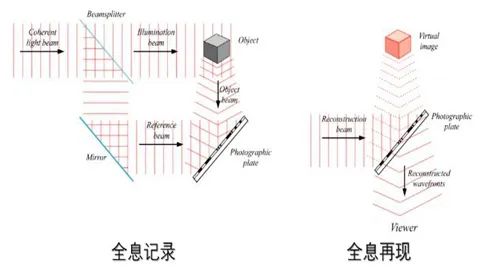
第三是偏振。偏振乍一看似乎找不到那个相位,但是深入分析一下就知道,偏振有偏振度和偏振角两个量,其中偏振角就可以等效看作相位。
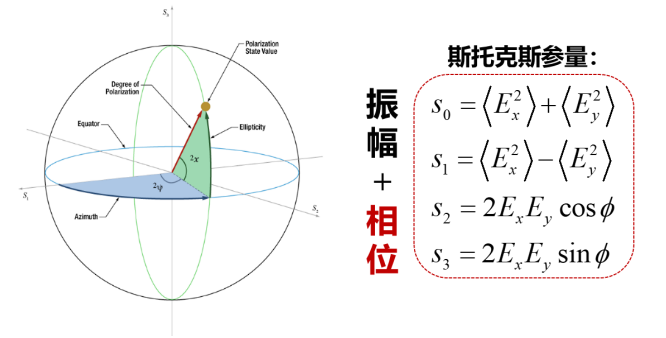
第四是结构光成像。我们知道,当平面波投射到物体表面时,遵循菲涅尔定律产生折射和反射,物体表面的起伏会产生相位的变化,将不再是平面波,记录下此时的波前,便能够恢复出物体的三维形貌。这是教科书的表述方式,实验却没那么容易。
我们希望在自然环境中也能够记录相位,实现三维成像。其实很简单,采用结构光照明,典型的就是黑白相间的平行条纹,投射到物体表面,就能看到条纹的形变,这种形变恰恰是我们通过照明的方式引入的相位;记录下条纹形变,就可以解析出相位,从而重建三维形貌。
第五是大气和水等混沌介质,这种我们可以称为“计算介质”的东东,在成像中往往起着很坏的作用,大气扰动会使天文望远镜看不清目标,于是就产生了自适应光学;还会产生散射,我在上一篇里已有论述。 第六是傅里叶变换。傅里叶变换也是复数形式,有频谱图和相位图;图像傅里叶变换相位图代表的是图像的位置和结构信息。
在计算光学成像中,我们经常遇到的是在频域里处理信息,就会与傅里叶相位打交道,散斑自相关成像就是典型的案例,其相位恢复就是恢复傅里叶变换相位。傅里叶望远镜当然关系更大了。
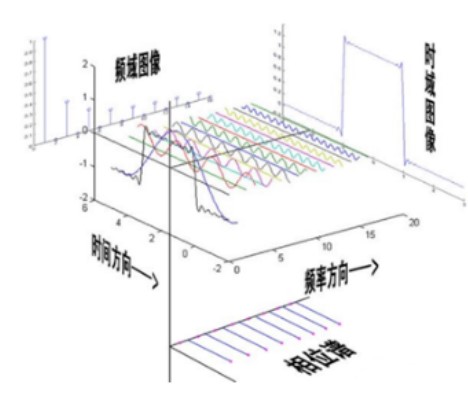
数学的傅里叶变换
还有一种是相关运算引入的相位。其实可以把相关运算看作与傅里叶变换是一样的东西,只是一种拓展而已。
再进一步看,其实还有很多与相位相关的,比如有像差的光学系统、多目相机、微透镜阵列、多角度照明等,都有相位的引入。只是,这些相位有的是“坏”的,我们不想要的,比如像差,而有的是我们想要引入的“好”的相位,比如多角度照明。
上面说了这么多,那相位到底能干什么?
2
相位能干什么?
首先,相位属于高维度的物理量,高维度的信息经过好的处理,投影到低维度,一定会有好的结果,这当然要看我们在低维度空间到底想要什么。专栏的第一篇里已讲到,光电成像朝着“更高、更远、更广、更小、更强”的目标发展,从应用的维度上看,我们需要把偏振、光谱、相位等高维度的物理信息转换为分辨率、作用距离、视场、重量体积和环境适应能力等,当然还有深度信息。

维度信息效能雷达图
下面就讨论一下“相位”在计算光学成像中的法力。 从相位本身的物理意义上来看,它是表征“相对位置”的一个物理量,那就天然地就决定了它具备与位置相关的能力,比如全息就是一个典型的例子。那么,相位在三维成像、提高成像分辨率、简化光学系统设计和提高环境适应能力等方面能发挥什么作用。
三维成像方面的相位
全息成像真正拉开了三维成像的序幕,从全息干板到现在的数字全息,都离不开相位,只是干板记录的是干涉条纹,通过光源照射还原相位信息,能看到真实的三维图像,而且,即使干板打碎,每一个小块都记录了物体的全息图,只是分辨率下降了;而数字全息则通过光电探测器记录全息图,借由标量衍射理论从干涉强度图里恢复出相位,从而达到全息的目的。
光电成像和显示,一定要走向三维!而光电成像实现的二维图像,没有深度信息,就谈不上三维。那如果能记录下或者恢复出相位,可否像全息成像,重建出三维的图像呢?答案是肯定的。 利用非相干光进行三维的成像的例子有:双目立体视觉、结构光照明三维成像、偏振三维成像和散射成像等。
双目立体视觉是利用视差和三角几何关系实现的,只是深度计算模型按照理想相机建立的,实际应用时,需要对双目相机进行标定,得到内外参数和相应矩阵。这个应用与相位无关。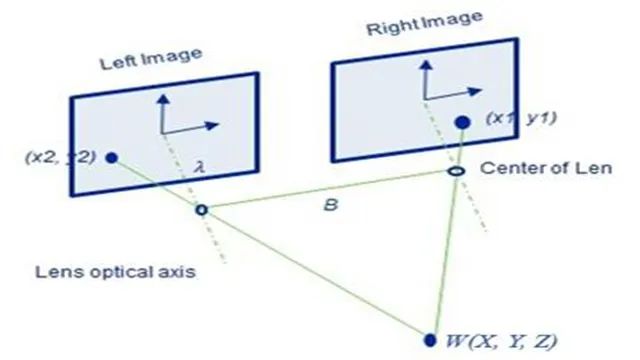

双目立体视觉
结构光照明三维成像是采用正弦条纹、格雷码和随机纹理等编码图案的主动照明方式,引入相位信息,当然,我们也可以采用时间编码方式。
以正弦条纹为例,将正弦条纹通过投影设备投影至被测物后会发生弯曲形变,根据弯曲程度可以解调得到相位,再将相位转化为全场的高度。这就是结构光三维成像的基本原理,其他的编码形式与此类似。
很显然,这种方法与全息不同,只能对结构光照到的形貌进行三维重建,这意味着只能从一个方向观测,它是三维的,但不具有“全息”特性。
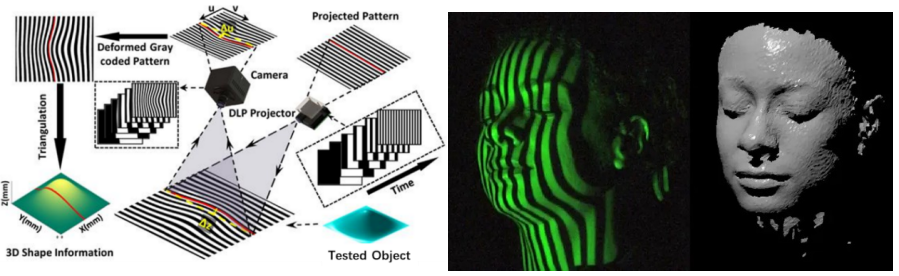
基于格雷码图案投影的结构光三维成像技术
偏振三维成像本质上利用偏振角信息重建三维形貌,这个偏振角其实也是相位,在第四篇文章已有论述。 我们知道,散射光场具有“全息”特性,一方面,我们可以从散射场中解译出相位信息,从而获得景深数据,实现三维重建;另一方面,选取一小块散斑也能解译出物体信息,只是分辨率下降了,这与全息很像。其实,我们从另外一个角度看,散射可以认为是一种特殊的结构光编码形式,既有幅值的调制,也有相位调制。这既是散射成像的魅力,也是挑战,需要我们更好地去发掘。
提高成像分辨率的相位
1953年,荷兰科学家泽尼克因发明了相衬(Phase Contrast)显微镜获得诺贝尔物理学奖,这是第一个把相位变成强度的成像案例,其原理是利用光的干涉原理,将相位差转换成振幅差(即明暗差)的显微镜装置。相衬显微镜实际上是把人眼看不到的相位信息转换为强度,可以解决透明物体的成像问题。
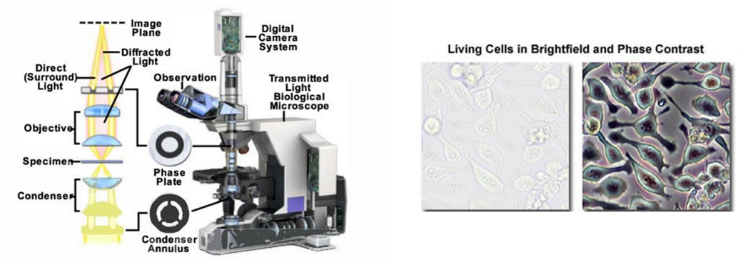
相衬显微镜与成像结果
那么能不能利用相位提升分辨率呢?这几年一直在流行“相位成像”,就是从强度中恢复相位信息,主要两种手段:一种是相干光照明,根据光的衍射理论,光的相位能影响到强度信息,可以通过在光路中引入某些光学元件使得相位能够反应在图像上,记录下相衬;另外一种是通过已知的强度信息,利用傅里叶光学原理解译出相位,称之为定量相位成像(quantitative phase imaging)。
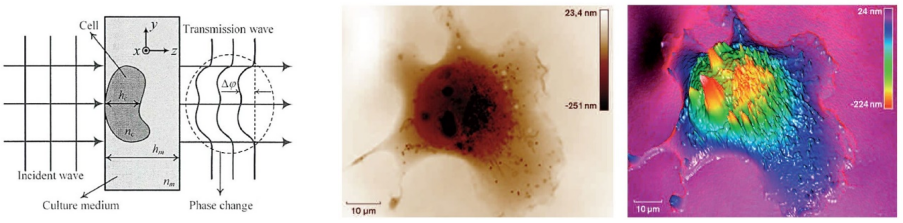
相位定量测量原理与细胞的定量相位成像
说起分辨率,就必须要说说阿贝衍射极限,光学成像分辨率可以表示为δ=kλ/NA,其中k为系数,如0.61,λ为波长,NA为数值孔径。从公式上来看,提升分辨率的手段基本上就是减小波长,提高数值孔径。很显然,对大多数成像而言,数值孔径更重要。提高数值孔径除了常规的增大光学口径和油浸介质等手段外,采取的方法都与相干有关,而相干必然离不开相位。
常见的结构光照明成像、叠层成像、散射成像和合成孔径成像,都离不开相位。关于这些内容,我想在之后的文章里专门讨论。 现在我们要思考的是能不能把相位这个高维度的量投影到分辨率这个维度,能否提升分辨率?可以。看一个现实的例子:人的双目视力是超过单只眼睛的,原因就是这里有视差,从而引入了相位,在大脑视觉合成时提升了分辨率。
这个是不是很有意思?在这里,我问一个问题,这个相位是什么?如何引入的?还有哪些方法,能够把相位与分辨率紧密结合起来?
简化光学系统设计的相位
光学系统设计的本质是对相位的优化控制,传统的光学系统为了减小像差采用多片镜片的组合优化设计,带来了好的像质也牺牲了体积、重量和加工成本。
在计算光学系统设计中,简化光学系统的核心必然是相位的混叠和解译。说起来很简单,在光学系统中减少了镜片,增加了编码过程,这都会引入相位的变化;如果把成像看成线性模型,那么解译就是求共轭矩阵的过程,使之能够恢复到传统光学成像的效果;如果是非线性模型,那就应该考虑减少镜片和编码过程引入的相位变化,可否做景深的延拓和分辨率的提升。
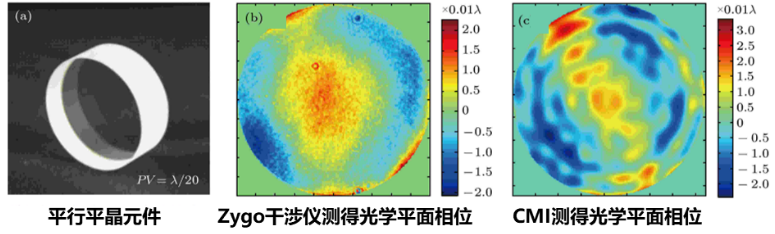
光学器件的相位 这就好玩了。你想啊,你用了廉价的方法,既减小了体积重量,还能三维成像,并且分辨率还能提升,是不是做梦啊?从理论上来讲,这还真能做到,但是还有很多的问题需要克服,比如能量减弱带来的对比度下降、数字信号处理引入的噪声和伪重建、光谱的混叠和相位的混叠等等复杂问题,当然还有相位信息不足的问题。从本质上来讲,还是多维度物理光场的问题。
提升环境适应性的相位
大气扰动、雾霾、烟尘、水等介质都会引起相位的变化,从而造成图像畸变、看不清、看不远等问题。自适应光学实际上就是在解决相位的问题。但是,自适应光学也存在着自身的局限性,除了需要信标光之外,一是用不起,二是也不一定都能解决问题。这实际上又回归到了光场的问题,目前来看,散射成像应该是解决环境适应性最好的办法了,说到底还是一个相位恢复的问题。
当然,还可以异想天开一点,想办法再引入一点其他的因素,也能够更好地解决问题。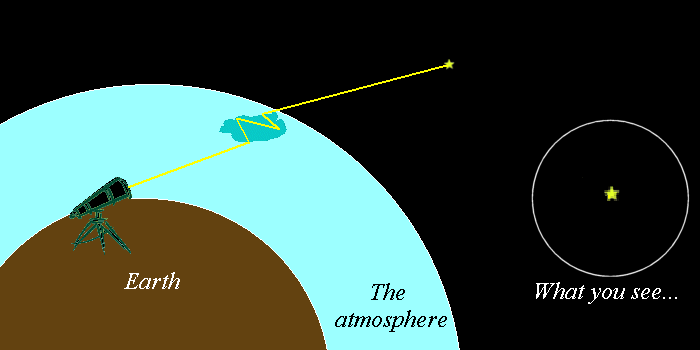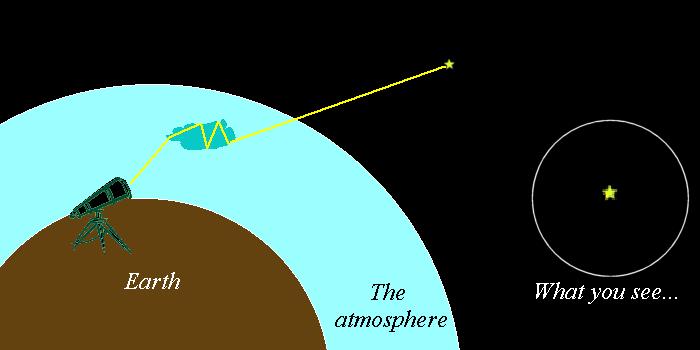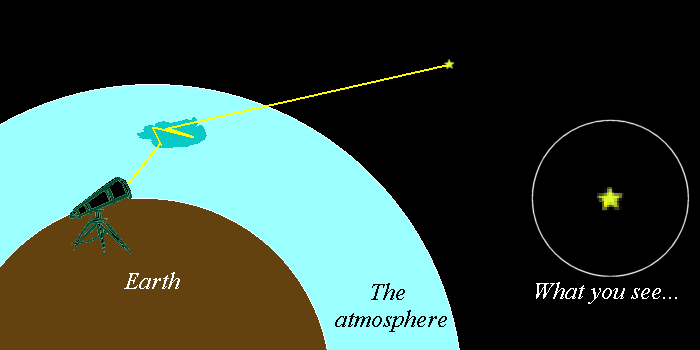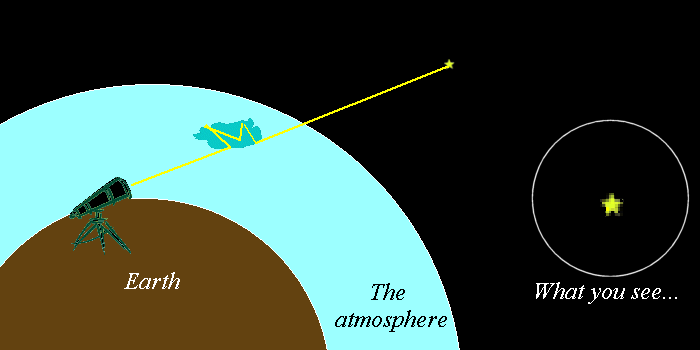
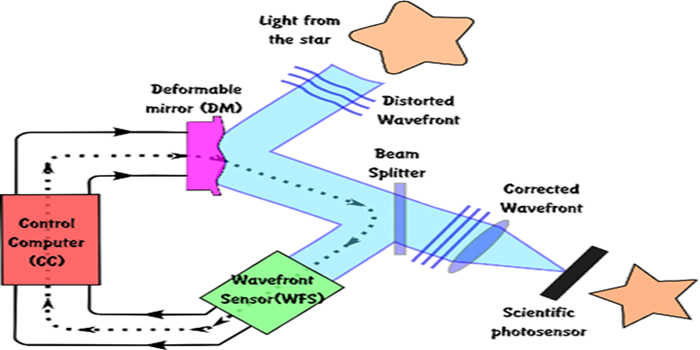
应对大气扰动的自适应光学
我们还可以挖掘相位其他方面的潜力,比如能否在拓展视场方面发挥作用,解决“更广”的问题?我一本正经地告诉你:我不知道!但直觉告诉我,应该有路可走。你再问我为什么,我只能一本正经地告诉你:我可能看的书比你多。 其实说了这么多,核心的问题还是最终回归到了多维度物理光场的问题。如果说现在很多方法好像疗效不太好,我再告诉你:那是因为我们现在都是采用的线性模型,那个非线性的成像模型还在路上,但我看到,它越来越近了!
3
怎么用好相位?
前面我们讲了计算成像中相位的类型和相位都能干哪些事儿,那我们是不是就能用好相位呢?该怎么使用相位呢? 要回答这个问题首先要搞明白你要处理的那个相位到底是“谁”的相位,谁的钥匙开谁家的门;然后看相位要解决什么问题,对症下药。但是,目前面临的问题可能有两类:一类是有相位不知道怎么用,一类是没有相位。
在这里,我们先把相位当作阿堵物(钱)吧。地主家的傻儿子给他再多钱他都不知道怎么用,相反,钱越多他越危险。解决问题的办法是娶个好媳妇。可是,哪个好姑娘会喜欢一个傻子啊?!那就找一个好管家,给他梳理梳理。对于相位也是,很显然这个高维度的信息一定带着神秘的力量来到你身边,你却不知道珍惜!我们也需要问道上天,问相位这位神仙姐姐究竟能干啥,该怎么干。
如果一个不名一文的穷小子,不努力挣钱必然死路一条。解决问题的方法就是要找到一条致富的道路,不能光是吃饱喝足就不求上进了!哎,想想我自己也经常偷懒,真是罪过啊!阿弥陀佛!对于没有相位而言,那就是想办法引入相位,比如结构光照明。同样,对于相位余额不足的,目前多采用焦面前后微移动拍摄多组数据,以更好地恢复光场。
你是不是觉得还是做一个挣钱够花就行的人就好,想用多少挣多少。可惜,现实生活中的这种月光族,往往不敢对生活有奢求。相位的引入也是如此,还是宽裕一点吧,你可能根本不知道相位的深浅。你不想努力?来来来,小子,多走一步:人和废旧物资回收站。
有人问:毛玻璃贴上胶带就变成透明的是怎么回事?这其实就是相位补偿的问题,毛玻璃的随机起伏带来了相位的变化,你看不清楚;贴上胶带,由于胶合得比较好,正好做了相位的抵消,所以毛玻璃就变透明了。不信的话,你拿胶带去贴毛玻璃平的那一面,我敢跟你赌一毛钱,毛玻璃不可能变透明。其实,这个胶带在数学上就是毛玻璃矩阵的共轭矩阵。
审核编辑:刘清
-
电磁波
+关注
关注
21文章
1476浏览量
54049 -
傅里叶变换
+关注
关注
6文章
442浏览量
42784 -
光电成像
+关注
关注
0文章
11浏览量
6913
原文标题:相位,到底是个啥?
文章出处:【微信号:bdtdsj,微信公众号:中科院半导体所】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
相位测量仪工作原理,相位测量仪怎么使用

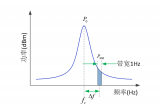
相位噪声分析仪的技术原理和应用
求助,关于LMK5B12204同步相位调整问题求解
TLV3501做的50HZ工频信号的过零比较,会带来相位的偏移有什么办法可以解决吗?
可以用OPA847做一个电压跟随器相位补偿电路吗?
电容和电感在电路中影响相位的原因
移相电路引起相位差的原因是什么
如何描述相位噪声的大小 相位噪声测试和意义




 计算成像里的相位都有哪些?相位能带来什么?
计算成像里的相位都有哪些?相位能带来什么?










评论