--基于格密码全同态加密的数学基础
此情此景,我想先吟诗二首:

从文学的角度看,以上两首诗比李白写的稍微逊色一点,不过,从数学角度来看,简直可以获得诺贝尔数学领域的文学奖(可惜了,目前还没有这个奖项)。
以上是定场诗,本文旨在尽量少用数学公式的情况下,解释清楚FHE(Fully Homomorphic Encryption,全同态加密)相关的数学基础。话不多说,我们继续。
一点定乾坤
当时的故事是这样的:
一个阳光明媚的下午,初三(一)班刚刚上完第二节数学课,老师讲的是函数相关的内容。阳光洒在我课桌上,温暖的光线散射到眼睛里,而我却盯着老师讲的抛物线函数图像,一动也不动。
当时我本子上的图像是下面这样的:
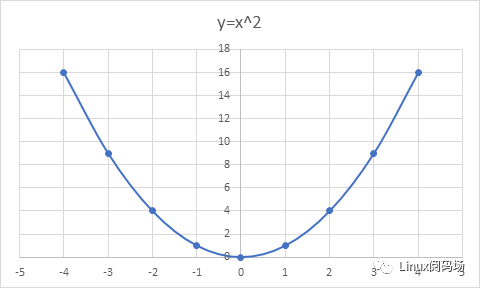
发呆的时候,我们班里的泰勒同学去完厕所从教室前门走了进来,我的座位正冲门口,可能是他发现了我在发呆,就径直走了过来,跟我说:
“干嘛呢?大白天的,发什么呆啊?”
“发呆跟白天晚上有关系吗?”我应道,“别打扰我,我在思考一个深奥的问题!”
“什么问题啊?别思考了,我跟你说个事儿,我会魔法你知道吗?”泰勒不仅没走开,反而挨着我坐了下来。
“别扯了,我们又不是幼儿园的小朋友,都初三了,谁还相信魔法?!”我有点不耐烦,打算继续思考我的深奥的问题。
“你别不信啊,我眼睛有透视的能力”泰勒有点不依不饶,继续说道:
“不信的话,你把你的草稿本合起来,别让我看到,我可以在不看你本子的前提下,知道你画的是什么函数”
“滚一边儿去,我没那闲工夫跟你玩儿”因为泰勒打断我的思路,想赶紧轰他走。
“实在不信的话,我们试试不就知道了吗?!”泰勒不仅没走,还挪了一下凳子,离我更近了。
“好吧,好吧,如果不灵的话,有多远滚多远,行不行?”我说。
“没问题,这样,你把你的函数图像用两本书遮起来,两书之间只留一个点,我可以根据这一个点的信息得到整幅函数图像!”泰勒显得有点兴奋。我自已也有点跃跃欲试。
“行啊,没问题,就给你留一个点,看你怎么猜!”我心想,别说一个点,就是给你十个点,你能猜出来的话,我也算你赢。
我边说边把草稿本打开,用语文书和英语书遮住,中间只留了一个小缝儿,我自己刚刚能看到横轴上‘1’对应的那一点点图像。
“行了,我准备好了,猜吧!”我说。
“好,现在正式开始,不过我要先问你几个问题”泰勒说。
“问吧,问吧!”我说。
“请问,在这个点,这个函数的一阶导数是多少?”泰勒正式开始了他莫名其妙的发问。
“一阶导数?是2”我略作思考,回答道。
“二阶导数呢?”泰勒继续问。
“还是2”我脑筋微转,答道。
“三阶导数呢?”泰勒继续问。
“三阶导数啊?是0”我快速说道。
“四阶导数呢?”泰勒还要问,没有停下来的意思。
“哎呀,你烦不烦,三阶导数后面所有的导数都是0”我说。
这时,只见泰勒嘴角上扬,微微一笑,说:“你画的函数是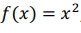 ,对不对啊?!”
,对不对啊?!”
“这怎么可能?!”我很是惊讶,仅仅通过一个点的信息,泰勒怎么会知道整幅函数图像的呢?
只见泰勒那时的表情,得意洋洋,心满意足,开始手舞足蹈。。。
我还是不信,怀疑刚才泰勒偷看到了我的草稿本儿。所以我又紧接着测试了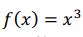 ,甚至还测试了
,甚至还测试了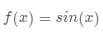 ,还有很多其它很复杂的函数,令人震惊的是,这些函数,无一例外,泰勒都只通过一个点就猜出来了。
,还有很多其它很复杂的函数,令人震惊的是,这些函数,无一例外,泰勒都只通过一个点就猜出来了。
“怎么样?这回相信我会魔法了吧?!”泰勒见我不解,轻飘飘撂下这句话就走开了,只留下凌乱的我,张着嘴巴,一脸懵。。。
“还真是啊,‘一点定乾坤’,难道说的就是这个?”我不禁自言自语。
读到这里,聪明的同学可能早就可以拆穿泰勒所谓的魔法了,不过我实在是愚钝,我们继续往下看。。。
一时含永远
泰勒同学前脚刚走,我的另外一个叫傅里叶的同学就跑了过来,他好像是看到了我和泰勒玩的游戏,跟我说:
“泰勒那哪叫魔法啊,我会的才是真正的魔法,我可以让时间停止,让瞬间变永恒”
“你跟泰勒一个德性,净扯玄乎儿的,把我当幼儿园小朋友耍”我还在琢磨刚刚泰勒是怎么做到的。
“你不相信的话,我们也做个游戏试试”傅里叶不想放弃展示他的魔法。
“没问题,直接开始吧,你说怎么玩?”我说。
“好,我的第一个问题是,当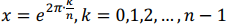 的时候,函数的值是多少?”见我同意玩,傅里叶也是开门见山,一下子问出了第一个问题,其实,也是唯一的一个问题。
的时候,函数的值是多少?”见我同意玩,傅里叶也是开门见山,一下子问出了第一个问题,其实,也是唯一的一个问题。
我奋笔疾书,毕竟x是个e指数,还包含三角函数的角度,但是,我真正计算才发现,根本用不到笔算,口算就可以。我都一一回答了。当然,在这过程中,我把本子捂得很紧,没敢让他偷看一眼。
“我知道了,你的函数是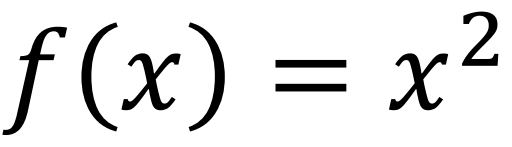 ,对不对啊!”傅里叶得意的问。
,对不对啊!”傅里叶得意的问。
“我K,你是怎么知道的?!,难道传说中的‘一时含永远’,说的就是你?!”我被彻底震惊了。
。。。
。。。
。。。
好吧,我承认,泰勒和傅里叶不是我的同学,上面的故事都是编的。我也是实在编不下去了,很多聪明的同学也早就发现了泰勒和傅里叶的秘密。
泰勒的秘密就是:
对于任何一个光滑函数,都可以表示为多项式的形式,而多项式的系数可以通过某一点的导数获得。
是的,你没看错,一个点竟然蕴含了一个函数的所有信息。
傅里叶的秘密是:
对于任何一个光滑函数,都可以表示为三角函数累加(积分)的形式,而每一项的系数可以通过多个点的自变量和因变量对儿(x, f(x))获得。
是的,你没看错,我们手机里的歌曲,不管你播不播放,他总是呆在那里,不曾改变。一个随时间变化的信号,经过傅里叶变换之后,时间将消失,音乐会上一段美妙的音乐,不过是乐谱的再一次重复,而无论重复多少次,乐谱从未发生丝毫改变。
以上被称为“感觉第一定理”。
对于喜欢看公式的同学(对于不喜欢看数学公式的同学,直接跳过公式部分,丝毫不用担心会影响你对本文的理解),就是:
泰勒公式一句话描述:就是用多项式函数去逼近光滑函数。
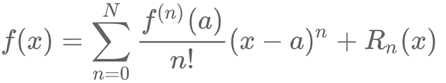
傅里叶变换一句话描述:将用一般多项式表示的时域的信号,变成频域的信号(这句不懂没关系,看完后面就懂了)。
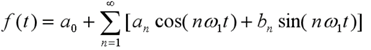
你在其它地方看到的傅里叶变换可能是下面的样子:
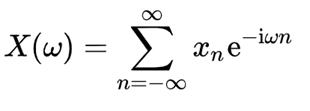
那是因为欧拉这位同学的存在,可以把e指数变成三角函数的形式。
欧拉公式:
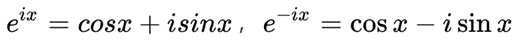
所以,我总结下来,就是,对于任何一个函数,都可以用一些简单的东西的线性组合得到。这里面提到的简单的东西,就可以认为是搭积木的一个个小积木块,用数学的语言,小积木块就是函数的基。用线性代数的语言,小积木块就是单位向量。而具体的函数,就是用小积木块搭出来的各种形状的积木,以及用单位向量组成的一般向量。
以上被称为“感觉定理-2”
弯路走的快
稍作休息,我又可以继续编故事了,还是续集。
傅里叶同学说完答案,同样留下一头雾水的我,潇洒的走开了。当时,我脑袋里真是一团浆糊,泰勒同学的秘密还没搞懂,又来一个傅里叶的秘密。秘密加秘密,我就更摸不着头脑了。
正当我一筹莫展之际,我的第三位同学-凯莱出现在了我的面前。还没等我张口请教,凯莱就发话了:
“泰勒和傅里叶的三脚猫功夫,有啥了不起的,在我看来,不就是多项式的两种表示形式而已。”
“多项式,我知道,不过,我只知道一种形式,另外一种是啥?”我问。
凯莱,不像泰勒和傅里叶,他举止优雅,阵脚不乱,简称“矩阵”(sorry,这是个谐音梗)。
“不用着急,听我给你慢慢说”凯莱搬了自己的凳子来,轻坐在我旁边。
你看啊,我们一般见到的多项式是下面这样的,叫多项式的系数表示法。
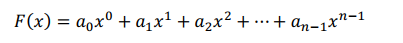
这其中的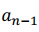 就是多项式的系数,所以叫“系数(coefficient)表示法”,没错,数学就是这么直白。
就是多项式的系数,所以叫“系数(coefficient)表示法”,没错,数学就是这么直白。
除了系数表示法之外,还有一种,叫“点值表示法(point-value representation)”,顾名思义,就是用这个多项式上的点,以及这点对应的值来表示。
比如,上面的多项式,用点值表示法,就是:
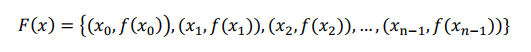
看到这里,我就有点不太理解了,为啥点值表示法也能代表这个多项式呢?凯莱,不紧不慢,耐心解释道:
你看啊,点值表示法里面的每一对点值,是不是表示下面一个等式,比如,第一对儿点值,表示的就是下面的一个等式。
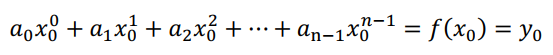
第二对儿点值对应的是下面的等式:
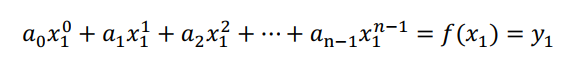
从点值表示法来看,本来在一个平面上有无数条曲线,每次确定一个点,就要求我们想要的曲线必须经过这个点,当我们确定的点的数量和这条曲线的次数(就是上面式子中的n)相同时,我们就找到了经过我们指定所有点的唯一一条曲线。这是“感觉定理-3”
这时,凯莱好像看出了我的心思,说:
“瞎想什么啊,太难理解了,我们初中生,刚学过矩阵,用矩阵表示比你那个‘真感情’容易多了!”
“什么意思啊?”我还是不太理解。
“你看啊。。。”凯莱又开始娓娓道来:
上面用点值表示法表示的多项式,每个点值对儿都对应一个方程,如果我们把他们组合到一起,写成矩阵的形式,不就是下面这个样子吗:
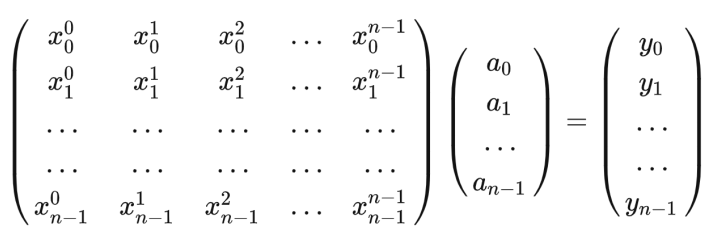
点值表示法,就是上面三个矩阵,第1个和第3个,分别表示“点”和“值”,第2个矩阵是多项式的系数。当其中第1个和第3个矩阵都确定的情况下,第2个系数矩阵其实也就确定了。所以,从这个角度看,点值表示法和系数表示法,只是同一个函数的两种表示方式,就好像同一个函数既可以按泰勒同学的方式展开,也可以按傅里叶同学的方式展开,两种方式描述的其实是一个东西。
就好像光的波粒二象性似的,泰勒同学强调的是粒子性,而傅里叶同学强调的是波动性。或者说,系数表示法强调的是函数的波动性,点值表示法更多体现函数的粒子性。此为“感觉定理-4”.
凯莱同学啰啰嗦嗦的说了半天,我也不知道说了些什么东西,就问:
“凯莱,你说的点值法,我是听懂了,可我没看出点值法有啥用处啊”
“这个用处可就太大了,可以加速多项式乘法!”凯莱说。
你看啊,比如,我们有两个用系数表示法表示的多项式:
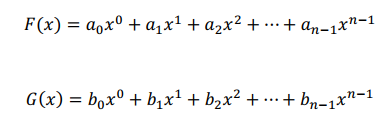
那么这两个多项式的乘法结果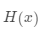 的计算过程如下所示:
的计算过程如下所示:
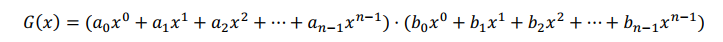
这个多项式乘法的复杂度是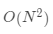 ,另外还要注意的是,“多项式乘法”中的“乘法”两个字非常容易产生误导作用,给人一种真的是普通乘法的错觉,其实,多项式的乘法操作,实际上就是卷积运算,这一点一定要谨记。
,另外还要注意的是,“多项式乘法”中的“乘法”两个字非常容易产生误导作用,给人一种真的是普通乘法的错觉,其实,多项式的乘法操作,实际上就是卷积运算,这一点一定要谨记。
“卷积?有什么特殊的呢?这和点值表示法有啥关系啊?”我还是似懂非懂的问。
“别着急啊,还记得刚刚走的傅里叶同学吗?他刚刚使用的秘密武器就是傅里叶变换,还记得吗?”凯莱问我。
“当然记得,傅里叶变换可以让时间消失的,太厉害了,可以将时域的信号,变成频域的信号!”我说。
“完全正确!”凯莱对我的回答非常满意,他接着说:
“多项式的乘法(也就是卷积运算),可以先将两个多项式分别做傅里叶变换,变完之后的两个式子,直接对应项相乘,对应项相乘完之后的结果再做傅里叶逆变换,得到的结果就是两个原始多项式的乘法结果!!!”凯莱兴奋的嚷道。
“这个我知道,这不就是卷积定理嘛!卷积定理说的是,在一个域的相乘等于另一个域的卷积,用式子表示,就是下面这样子的”我补充道。
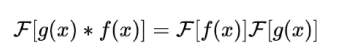
“可是,这个和你前面提到的矩阵有什么关系啊?!又和多项式的点值表示法有什么关系啊?!”我还是没完全理解凯莱的意思。
“不用着急,这两个问题很快你就明白了,只需最后一步!”凯莱还是慢条斯理的样子。
“最后一步?什么最后一步啊?”我问。
你看啊,其实啊,点值表示法有个非常大的好处,我之前没提到,就是:
对于用点值表示法表示的两个多项式的乘法(实际是卷积),可以直接对应项相乘即可,即,
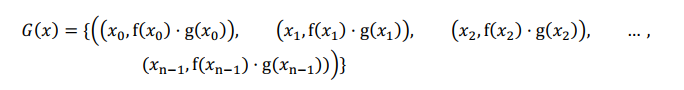
“我知道了,凯莱,原来复杂度为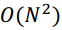 的多项式乘法运算,复杂度降低成
的多项式乘法运算,复杂度降低成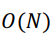 了”我好像发现了什么新大陆,也吼了起来。
了”我好像发现了什么新大陆,也吼了起来。
“不对啊,好像哪里不对啊,这个复杂度的降低要想实现,需要先把系数表示法变成点值表示法才行啊!,这个从系数转点值的复杂度也是啊,你这搞半天不是瞎搞了吗!本来可以有直行的路可以到达,你这越走越远啊!”我刚刚发现的新大陆瞬间又不香了,满脸狐疑的看着凯莱。
“不对啊,好像哪里不对啊,这个复杂度的降低要想实现,需要先把系数表示法变成点值表示法才行啊!,这个从系数转点值的复杂度也是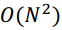 啊,你这搞半天不是瞎搞了吗!本来可以有直行的路可以到达,你这越走越远啊!”我刚刚发现的新大陆瞬间又不香了,满脸狐疑的看着凯莱。
啊,你这搞半天不是瞎搞了吗!本来可以有直行的路可以到达,你这越走越远啊!”我刚刚发现的新大陆瞬间又不香了,满脸狐疑的看着凯莱。
“你别着急啊,你再仔细看看,你说的没错,如果是一般的系数变点值,复杂度确实降不下来,可是,如果我取得点是一些特殊的点的话,情况就完全不一样啦”凯莱继续给我解释,不紧不慢。
“取什么样的点,才能降低复杂度呢?哦!我知道了,复数域的单位根,复数域的单位根,复数域的单位根!”我连续说了三遍,生怕凯莱听不清楚。
在复数域内,方程有个根,就叫单位根,这些根分别是:
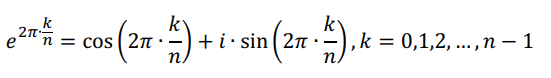
就是前面傅里叶同学表演“一时含永远”魔法的时候用的那几个点!!这几个点太好了,口算就能知道对应的函数值,这样的话,系数到点值的转换就简单多了。
“是的,你终于发现了傅里叶变换的另外一个秘密,就是傅里叶变换,其实就是多项式的系数转点值,当然,我们考虑的是离散的傅里叶变换(DFT)”凯莱继续说道。
“嗯,后面我就知道了,DFT有个快速算法,叫FFT,FFT的计算复杂度是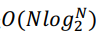 看到了希望,我又开心了起来。
看到了希望,我又开心了起来。
为了防止忘记,我在心里又重新梳理了一下多项式乘法的过程:
多项式乘法本质是卷积运算
卷积运算可以分三步:
a. 先把两个多项式从系数表示变成点值表示,这一步就是DFT,可以用FFT加速,FFT采用分治法,可以将一根很长的木棍儿每次都折半,这样递归下去,就可以降低计算复杂度。FFT选用的是单位根,NTT选用的是原根,目的一样,为了加速DFT, 相比于FFT,NTT还便于取模运算。
b. 然后,将用点值形式的两个多项式,对应项相乘,就得到了最终结果的点值表示形式。
c. 最后,还需要把最终结果的点值表示变回系数表示
“前几步上面都提到了,我也理解了,可这最后一步是怎么做到了?”虽然大部分的内容我理解了,可再三回忆,最后一步确实没听凯莱说过。
“哎呀,这还不简单吗?提示你一下,看看多项式的矩阵表示形式,对了,不用往上翻了,我们再写一遍,就是下面的样子”凯莱嘿嘿一笑:
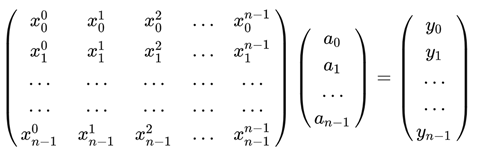
还是原来的配方,还是熟悉的味道。点值表示变回系数表示的过程,不就是已知上面的第1个矩阵和第3个矩阵,求中间的系数矩阵嘛?!
“原理我貌似有点懂了,可是,具体怎么求啊,我线性代数也学的不好”我继续追问凯莱,凯莱毕竟是矩阵理论的大师级人物,这点小问题应该难不倒他。果然,还不到1秒钟的时间,凯莱就发话了:
“这个问题嘛,等式两边都乘上第1个矩阵的逆矩阵就可以了,注意啊,是“矩阵的逆:”,不是”矩阵的转置:”,这个千万别混淆了”凯莱细心的提醒我。
“知道啦,不过,矩阵的逆,复杂度可很大啊,是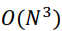 ,你这又是南辕北辙啊?!”我又有被凯莱耍了的感觉。
,你这又是南辕北辙啊?!”我又有被凯莱耍了的感觉。
“你说的没错,上面的第一个矩阵,是一个特殊的矩阵,叫范德蒙矩阵,一般的范德蒙矩阵的逆,运算复杂度也是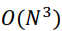 ,不过,但是,如果我们按照傅里叶同学的思路,搞出来的这个范德蒙矩阵是特殊中的特殊,它的逆矩阵,就是矩阵中的每个元素的共轭,再除以n,就是这么简单,哎哟,就是这么巧合,你说神奇不神奇”凯莱难得的大笑起来。用式子表示,就是下面这个样子的:
,不过,但是,如果我们按照傅里叶同学的思路,搞出来的这个范德蒙矩阵是特殊中的特殊,它的逆矩阵,就是矩阵中的每个元素的共轭,再除以n,就是这么简单,哎哟,就是这么巧合,你说神奇不神奇”凯莱难得的大笑起来。用式子表示,就是下面这个样子的:

这个矩阵的逆,就是:
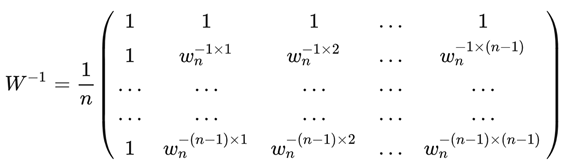
“原来如此,原来如此啊,如果我记得没错的话,点值到系数的变换过程就是传说中的傅里叶逆变换,也叫IDFT,这个也有加速版本的IFFT。”我终于恍然大悟,“弯路走的快”,诚不欺我,有图为证。
故事讲到这里,我不禁又想起了最开始的两首诗,史上最富含数学知识的文学作品,名副其实。不过,看标题,内容是同态加密啊,故事都讲到这儿了,嘚啵嘚啵唠半天嗑,咋同态加密的影儿都没看着啊?!
别着急,这是同态加密的上篇,我们稍作休息,请等待后面的精彩故事。
此情此景,我想再吟诗二首:

话说上篇我们了解到了很多非常重要的内容:
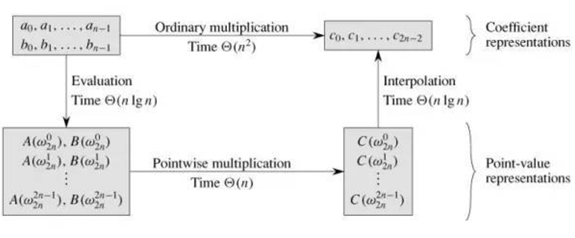
多项式从系数表示变成点值表示的过程,就是离散傅里叶变换(DFT/FFT)。
多项式从点值表示变成系数表示的过程,就是离散傅里叶逆变换(IDFT/IFFT)。
多项式的乘法,本质是卷积运算,一次卷积运算可以分为三步:Convolution=FFT->multiply->IFFT,即卷积定理表达的内容。
以上三种场景,都有相应的矩阵操作与之对应。原因是:一个多项式的点值表示和一个线性方程组对应,线性方程组又和一个矩阵乘法运算对应,这样多项式的乘法就可以转换成FFT相关的计算。这一点非常重要,是理解FHE的关键所在。
仔细思考上篇中讨论的内容,加上上面几点提示,这样我们就把FHE相关的几个非常重要的概念,以及这些概念之间的关系就搞清楚了,此时,我们的脑海里应该出现以下几个概念,并且这些概念不再是独立的孤岛,而是脑海里一片广阔的大陆:泰勒公式,多项式,系数表示法,点值表示法,DFT,FFT,卷积,卷积定理,线性方程组,矩阵,矩阵的逆。
好,收拾行囊,我们继续赶路,在正式向FHE山顶发起冲锋前,我们有必要加深一下对傅里叶变换的理解,如下图所示:
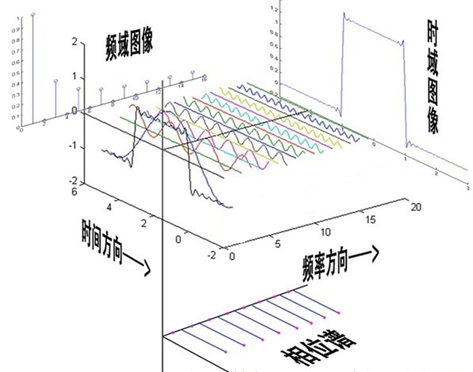
仔细查看上图。。。在观察这段时间里的某个时刻,一道金光从脑海划过:为什么时间消失了?!我们感知到的随着时间流淌的宇宙,进行傅里叶变换后会怎样?我们又该怎么选择傅里叶变换的旋转因子(twiddle factor)?如果你的脑海没有金光划过,可以先阅读一下。
如果脑海里实在是没有金光划过,也没关系,不会影响我们最终站上FHE的山顶。我们继续。。。
在FHE领域,我们可能会反复看到一句话:“FHE是基于格密码学的”。这句话很简短,既然反复看到,说明应该很重要,可是,我从这句话里面又看不出什么东西,每个字我都认识,但就是不知道整句话什么意思。什么道理都懂,仍然过不好一生。不用着急,我们慢慢拆解:
首先,这里面最难懂的可能是“格”这个字,于是,我们就百度里一下,“格”是这么定义的:
“ “格”是一种特殊的偏序集。”
也很简短,不过不出意外,还是每个字都认识,但仍然不明白整句话说的是啥意思。按道理,既然名字叫“格”,应该跟“格子”有关系啊?!
于是,我们继续查找FHE相关的资料,除了“格”这个东西,经常出现的还有“环”这个概念,于是百度之,“环”定义的第一个条件是:
“ 集合R在+运算下构成阿贝尔群” 此外还有“理想(Ideal)”两个字也出现在了附近。
也很简短,不过不出意外,还是每个字都认识,但仍然不明白整句话说的是啥意思。按道理,既然名字叫“环”,应该跟“铁环、手环”之类的东西有关啊?!
按图索骥,从“环”的定义里,我们发现了“阿贝尔群”这几个字,“阿贝尔”应该是个人名,那“群”又是啥意思?!,于是,继续百度之,
“在数学中,群表示一个拥有满足封闭性、满足结合律、有单位元、有逆元的二元运算的代数结构,包括阿贝尔群、同态和共轭类。”
这句话相比之前“格”“环”的定义稍稍多了几个字。欣喜的是,这句话中提到的几个概念好像都知道什么意思,比如“结合律”,“单位元”,“共轭”等,此外,还见到了我们苦苦追寻的“同态”两个字,相比最开始的漆黑一片,终于见到了几个火星儿,希望有了,胜利可能就在眼前。。。
于是,我们冲向FHE这个山顶的第一条路径就出现在了我们眼前,那便是:群->环->域->格。虽然只有四个字,可每个字看起来都不是那么好搞定的,毕竟,我们好像依稀听说过,“群论”,“环论”,“抽象代数”这几个可怕的怪物,这么陡峭的山体,一不小心就可能摔得粉身碎骨,永远达不到矗立在山顶的FHE。
我驻足沉思,难道到山顶只有一条路可走?难道必须从山脚下的“群”开始?现在都是新时代,出门爬个山,累了都有缆车啊, FHE这座山真有没有缆车可坐?如果FHE这座山没有缆车,那么FHE这座山附近有没有其它的山,如果有其它的山的话,有没有可能在两山的山顶建有“山顶缆车”?
一堆问题在我附近的空间里萦绕盘旋,我得不到回答,于是,在没看到“山顶缆车”之前,我开始从山脚下的“群”开始一步一步地爬。。。群是有点抽象,刚开始确实不太容易理解,不过我走得很快,不一会就建立了“群,环,域”的简单概念。
继续爬。。。
爬呀爬。。。
。。。
。。。
。。。
几天以后。。。
又有一道金光划过我脑海的上空,原本漆黑的海面上变得亮了起来。这道金光就是:
“很多格子摆在一起,看起来很像矩阵啊!”
是的啊,确实很多格子排列在一起,从远处看,就是一个矩阵啊,所以,“格”和“矩阵”之间一定存在某种关系!这个关系,不就是两座山顶之间的“山顶缆车”吗?!
“矩阵”,我们是比较了解的,如果矩阵和格之间建有山顶缆车的话,岂不美哉。
稍作验证,果不其然,我的想法是对的,“山顶缆车”早已建成,因为我看到了“整数格”的定义:
“离散的基向量生成空间集合,称之为整数格(Integer Lattice)”
这里面可能稍有难度的是“生成空间”,我们先来搞定它。
在线性代数中,如果我们要描述一个线性空间的话,我们需要先找到这个空间的一组基(Basis)。(PS:看到“基”这个字,你是不是又想起了傅里叶,想起了泰勒,想起了点值法,想起了消失的时间。。。)
比如常见的二维平面空间(笛卡尔坐标系),我们可以选用x轴和y轴的单位向量,作为我们的基向量(或者叫单位向量),分别是:
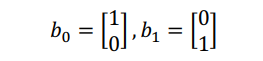
这样的话,任何XY坐标系的向量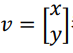 都可以用上面的一组基来表示。即,
都可以用上面的一组基来表示。即,
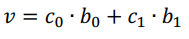
其中c_0和c_1可以是任意实数,如果是任意实数,那么v的所有可能的组合,就可以铺满整个二维平面空间,我们管所有的v组成的这个线性空间,就叫做,b_1两个基向量的线性生成空间(Span)。
我们不难想象,如果c_0和c_1是实数,那么b_0,b_1的生成空间是“连成一片”的,可以叫“片”,但是,如果c_0和c_1是只能是整数的话,那么b_0,b_1的生成空间就由“片”变成了无数个离散的“点”,这些点整齐的排列在一起,非常像无数个小格子,我们把这样的一个离散的生成空间,叫做“整数格(Integer Lattice)”。
果不其然,从“矩阵”到“格”,只有简单的一步,这个“山顶缆车”建得实在是太好了。
乘坐这条意外发现的缆车,我们快速抵达了“格”,这时,我们离FHE的核心腹地--LWE只有一步之遥了,加油,胜利就在眼前。

稍微瞄一眼上图,我们就会发现,这确实是很多格子啊,“格”这个字用的还是挺好的。
有了Lattice(格),就有很多跟Lattice 有关的有意思的问题就出现了。比如,想要表达一个向量v:
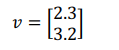
我们会发现,这个向量没办法在整数格中表达它,因为整数格中的系数必须是整数才行啊。
好了,问题来了,既然不能用整数格完美表达v,那么,是否可以找到一个最接近v的v_0,而v_0可以用整数格完美表达。对于上面的例子:
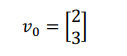
这个就是著名的CVP(Closest Vector Problem)难题!!
你可能会说,这算哪门子难题啊?我一秒钟就破解了。
没错,如果只是二维正交基向量的格,那么CVP问题不是特别难,但是,如果基向量不正交呢?如果v的维度变大到, 的成员的值变大到需要1000bit呢?
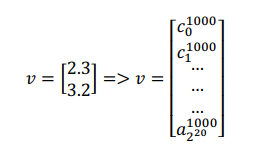
这个难度是被严格证明的,CVP问题是非常难解决的(Nondeterministic Polynomial hard, NP-hard)。
是的,这个乍看起来很简单,实际上很难的问题,就是格密码学的开端。
“什么?!搞了这么久,我以为已经达到了顶峰,竟然被你说成是‘开端‘?!!”
“是的,的确是格密码学的开端,现实就是这么的残酷,你以为的天花板,很可能只是别人的起点。比如,你家的天花板,可能只是楼上的地板,…^_^”
不过不要气馁,前面就是我们要找的LWE了。
在正式引入LWE之前,我们先回顾一下,送我们快速到达“格”的山顶缆车—矩阵。
是的,通过上篇的学习,我们早就知道了,一个矩阵乘的式子,对应一个线性方程组: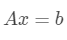
其中A是一个矩阵,x是一个向量,b也是一个向量。
已知A和b,求x的过程,就是求解线性方程组的过程。具体就是在上篇提到的方法:等式两边都乘以的逆矩阵,乘完之后,等式左边就只剩下我们要求出的未知向量了。
现在稍稍把上面的矩阵乘法等式变化一下: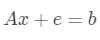
其中e是一个在固定数值范围内随机采集的一个随机噪音向量。这时,之前“等式两边都乘以A的逆矩阵”的方法就不行了,那我们怎么求呢?答案很简单:
“只能暴力破解”
也就是一个一个的猜x这个向量里的值,然后逐渐逼近。
这就是我们苦苦寻找的LWE(Learning With Error)问题!即:
已知一个矩阵,和它与一个向量相乘得到的乘积再加上一定的误差,也就是,如何有效的还原(learn)未知的向量。
“什么?LWE的定义这么草率吗?”
“是的,有时候胜利来得就是这么突然。”
“LWE,我们是知道了,可前面为啥提到CVP问题啊?”
如果我们细心的看LWE的问题描述的话,可以发现,LWE问题与我们之前提到的CVP问题有着惊人的相似。
不能说相似,简直一模一样。都是需要找到一组“系数”--,使得一组基向量--的线性组合,无限逼近我们想要的目标向量--。这里我们使用误差噪音--的大小来定义到底我们需要距离目标向量多近。
所以,如果CVP是一个NP-hard问题的话,那么LWE问题也是一个NP-hard问题了。
现在,我么是时候展示一下LWE问题的数学定义了:
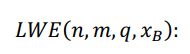
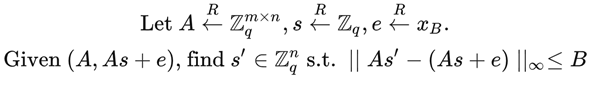
是不是猛一看,一堆乱七八糟的数学符号,想直接跳过去?莫慌,其实很简单。此外,这几个数学符号会反复出现在FHE有关的论文中,我们是绕不过去的。
从上面的学习中,我们知道,一个LWE问题中,包含以下几步:
第一,我们需要定义矩阵A的维度--m×n,其中m代表了整个线性方程组包含几个方程,而n代表每个方程中有几个未知数,也称为“安全系数”。n越大,LWE越难,m越大,LWE越简单。
第二,我们需要决定有限整数域中的,一般会选择一个很大的素数。越大,LWE越难。
第三,我们要决定叠加的噪音的取值上限。越大,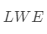 越难。
越难。
第四,上面三条已经足够,不过,为了简单,我们一般只设置一个参数n,然后通过一个函数计算出一组合适的m,q,B,可以保证LWE问题实例很大概率会拥有唯一的解,一般m,q都是n的多项式倍数(m=poly(n))。
我们定义了这些参数之后,LWE问题就好理解了:已知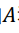 和
和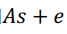 ,求未知向量s。其实,还是我们前面反复看到的这个矩阵乘法等式:
,求未知向量s。其实,还是我们前面反复看到的这个矩阵乘法等式:
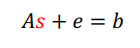
此情此景,我就不再吟诗了。。。
到此为止,其实我们已经掌握了FHE的绝大部分内容了,万事俱备,东风也不欠了,现在我们正式构建一个我们自己的同态加密系统。
首先,一个典型的HE系统包含以下几步:
第一,密钥生成(KeyGen)
第二,加密(Enc)
第三,解密(Dec)
第四,同态运算(Eval)
我们下面通过一个具体的例子来说明如何构建一个HE系统。
首先,KeyGen(),我们先随机生成一个私密向量s,然后在这个向量的最下面加一个“-1”,变成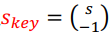 ,对,没错,就是这么草率,就是密钥。
,对,没错,就是这么草率,就是密钥。
然后,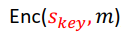 ,其中 m是我们要加密的明文-一个数。我们通过以下方式计算密文:
,其中 m是我们要加密的明文-一个数。我们通过以下方式计算密文:
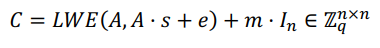
其中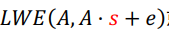 就是我们上面提到的LWE问题,A是随机生成的矩阵,s是我们第一步KenGen()生成的,e是一个随机噪音,所以LWE(A,A·s+e)的结果是一个看起来乱七八糟的
就是我们上面提到的LWE问题,A是随机生成的矩阵,s是我们第一步KenGen()生成的,e是一个随机噪音,所以LWE(A,A·s+e)的结果是一个看起来乱七八糟的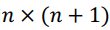 的矩阵。
的矩阵。
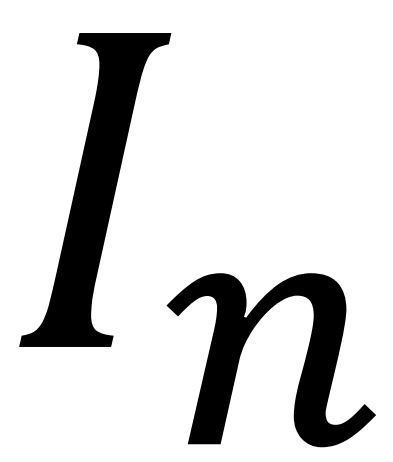 是一个
是一个 单位矩阵。
单位矩阵。
一个 矩阵C就是我们对加密之后的密文。
矩阵C就是我们对加密之后的密文。
第三步,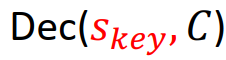 ,在解密时,对于一个密文矩阵,我们只需要计算
,在解密时,对于一个密文矩阵,我们只需要计算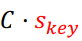 ,就会得到
,就会得到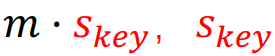 我们是我们的密钥,是已知的,所以,明文m就水落石出了。不知道各位在这时有没有想到矩阵的特征值和特征向量这两个概念。这里,密钥是特征向量,明文是特征值,所以不加噪声的话,明文实际上是在裸奔,毕竟求一个已知矩阵的特征值和特征向量还是很容易的!
我们是我们的密钥,是已知的,所以,明文m就水落石出了。不知道各位在这时有没有想到矩阵的特征值和特征向量这两个概念。这里,密钥是特征向量,明文是特征值,所以不加噪声的话,明文实际上是在裸奔,毕竟求一个已知矩阵的特征值和特征向量还是很容易的!
第四步,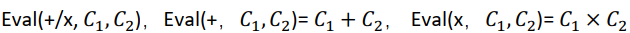 ,即,密文直接加、乘就可以了。这里需要注意的是,密文下的乘法运算可能会将噪音放大,导致解密失败,为了提高成功解密的概率,我们可以将和,进行二进制分解(就是用只包含0、1的二进制表示)。
,即,密文直接加、乘就可以了。这里需要注意的是,密文下的乘法运算可能会将噪音放大,导致解密失败,为了提高成功解密的概率,我们可以将和,进行二进制分解(就是用只包含0、1的二进制表示)。
如果你看到了这里,那么恭喜你,已基本掌握了FHE的精髓,最后,我们用下图来结束本文:
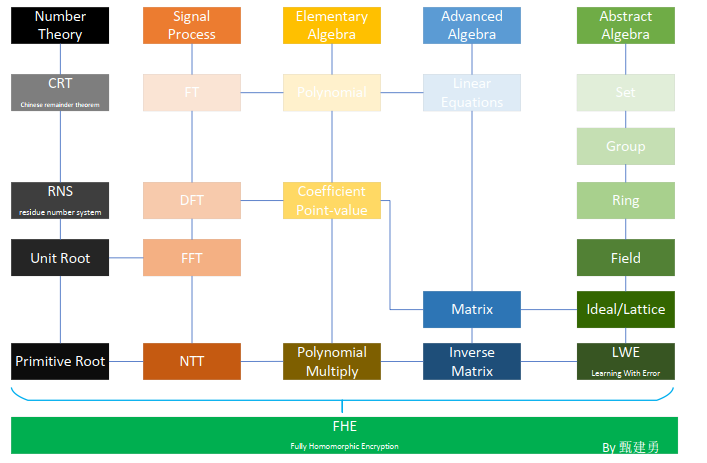
我定睛观察上面的图,持续十分钟,然后闭上眼睛,这时图中的格子忽然动了起来:
Polynomial、Point-Value、Convolution、DFT、FFT、NTT、UnitRoot、PrimitiveRoot、Matrix、Lattice、LWE。。。
这些原来一个个相互独立的单词,忽然间变成了一个个精灵,他们开心的跳着欢快的舞步,旋转、跳跃、相互握手,点头致意。。。
。。。
。。。
。。。
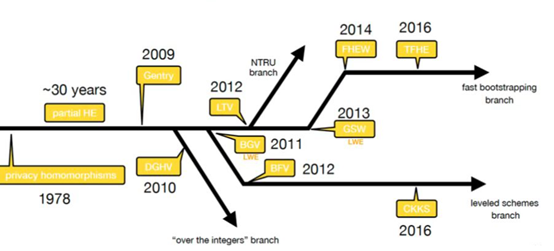
最后的最后,送上一幅藏宝图,祝一路顺风:
审核编辑:刘清
-
傅里叶变换
+关注
关注
6文章
442浏览量
42732 -
三角函数
+关注
关注
0文章
14浏览量
6779 -
同态加密
+关注
关注
1文章
5浏览量
1931
原文标题:看完这篇文章,还搞不懂全同态加密,你过来打我--基于格密码全同态加密的数学基础
文章出处:【微信号:LinuxDev,微信公众号:Linux阅码场】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
加密算法的选择对于加密安全有多重要?
常见的加密算法有哪些?它们各自的优势是什么?
对称加密技术在实际应用中如何保障数据安全?
NAS重置密码攻略来袭,让你告别‘密码焦虑’!
PostgreSQL将不再支持MD5密码
Linux系统设置用户密码规则(复杂密码策略)方法
艾体宝洞察 一文读懂最新密码存储方法,揭秘密码存储常见误区!
拥有SHA-256核心和32Kbits的EEPROM应用的加密芯片-GEN-FA

SSID和密码是否以加密形式存储在ESP8266中?
请问ESP32使用AT固件如何让配对密码大于6位?
MySQL忘记root密码解决方案
AES加密协议是什么?AES加密协议的应用
什么是TLS加密?TLS加密的功能特点
指纹加密移动硬盘详细方案解析




 基于格密码全同态加密的数学基础
基于格密码全同态加密的数学基础










评论