LC振荡器基础知识

LC振荡器将直流输入（电源电压）转换为交流输出（波形）。该输出波形可以具有各种不同的形状和频率，并且可以是复杂的形状，也可以是简单的正弦波。

振荡器的用途十分广泛，产生正弦波、方形、锯齿波或三角波，或者一系列可变或恒定宽度的重复脉冲。LC振荡器因其良好的相位噪声特性和易于实现而常用于射频电路中。

振荡器基本上是具有“正反馈”或同相的放大器，电子电路设计中的许多问题之一是在试图让振荡器振荡时阻止放大器振荡。

振荡器之所以工作，是因为它们通过将所需频率的直流能量施加到该谐振器电路中，克服了同一电路中电容、电感或两者形式的反馈谐振器电路的损耗。换句话说，振荡器是一种放大器，它使用正反馈产生输出频率，而无需使用外部施加的输入信号。

因此，振荡器是自维持电路，以单个正弦频率产生周期性输出波形。因此，任何电子电路要用作振荡器，它必须包含以下三个特性。

放大

正反馈

A 频率决定反馈网络

振荡器有一个小信号反馈放大器，其开环增益等于或略大于1，用于振荡开始，但要继续振荡，平均环路增益必须恢复为单位。除了这些电抗元件外，还需要运算放大器或双极晶体管等放大器件。

与放大器不同，不需要外部交流输入信号即可使振荡器工作，因为直流电源能量由振荡器转换为所需频率的交流能量。

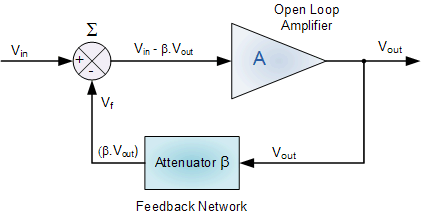
基本振荡器反馈电路

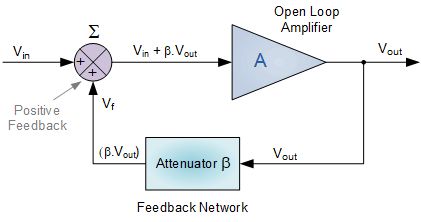
其中：β是反馈系数。

无反馈振荡器增益

带反馈的振荡器增益

然后振荡器是以所需的单个频率产生连续电压输出波形的电路。电感器、电容器或电阻器用于形成频率选择性谐振电路，该电路基本上是一个允许所需频率通过的无源带通滤波器和一个反馈网络。

反馈网络将一小部分输出信号“馈送”回输入端，以保持电路振荡。使用的正反馈量必须足够大，以克服任何电路损耗，以便无限期地持续振荡。

反馈网络基本上是一个衰减电路，其电压增益小于1（β <1）。振荡在Aβ>1时开始，一旦振荡持续，就会恢复统一（Aβ = 1）。

LC振荡器频率使用调谐或谐振电感/电容（LC）电路进行控制，产生的输出频率称为振荡频率。通过使振荡器反馈成为无功网络，反馈的相位角将随频率变化，这称为相移。

基本上有振荡器的类型

正弦振荡器– 这些被称为谐波振荡器，通常是“LC 调谐反馈”或“RC 调谐反馈”型振荡器，可产生幅度和频率恒定的纯正弦波形。

非正弦振荡器– 这些振荡器被称为松弛振荡器，可生成复杂的非正弦波形，从一种稳定条件到另一种稳定条件变化非常快，例如“方波”、“三角波”或“锯齿波”型波形。

振荡器谐振

当对由电感器、电容器和电阻器组成的电路施加恒定电压但频率变化时，电容器/电阻器和电感器/电阻电路的电抗由于所用元件的电抗，与输入信号相比，输出信号的幅度和相位都会发生变化。

在高频下，电容器的电抗非常低，作为短路，而电感的电抗作为开路时很高。在低频时，情况正好相反，电容器的电抗充当开路，电感的电抗充当短路。

在这两个极端之间，电感器和电容器的组合产生具有谐振频率（ƒr）的“调谐”或“谐振”电路，其中电容和感抗相等并相互抵消，只留下电路的电阻来反对电流流动。这意味着没有相移，因为电流与电压同相。考虑下面的电路。

基本型LC振荡器谐振电路

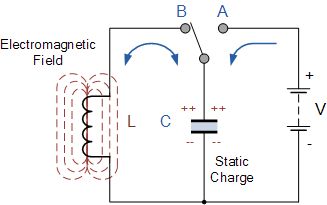
该电路由电感线圈L和电容器C组成。电容器以静电场的形式存储能量，并在其板上产生电位（静态电压），而电感线圈以电磁场的形式存储其能量。通过将开关置于位置A，电容器充电至直流电源电压V。当电容器充满电时，开关变为位置B。

带电电容器现在并联连接在电感线圈上，因此电容器开始通过线圈自行放电。随着通过线圈的电流开始上升，C两端的电压开始下降。

这种上升的电流在线圈周围建立一个电磁场，抵抗这种电流。当电容器完全放电时，C将原来存储在电容器中的能量完全放电，C作为静电场现在存储在电感线圈中，L作为线圈绕组周围的电磁场。

由于现在电路中没有外部电压来维持线圈内的电流，因此随着电磁场开始崩溃，电流开始下降。线圈中感应反电动势（e = -Ldi/dt），保持电流沿原始方向流动。

该电流以与其原始充电相反的极性对电容器C充电。C继续充电，直到电流降至零，线圈的电磁场完全崩溃。

最初通过开关引入电路的能量已返回到电容器，电容器在其两端再次具有静电电压电位，尽管它现在的极性相反。电容器现在开始通过线圈再次放电，整个过程重复。随着能量在电容器和电感器之间来回传递，电压的极性会发生变化，从而产生交流型正弦电压和电流波形。

然后，该过程构成了LC振荡器谐振电路的基础，理论上，这种来回循环将无限期地持续下去。然而，事情并不完美，每次能量从电容器C转移到电感器，L和从L转移到C时，都会发生一些能量损失，随着时间的推移将振荡衰减到零。

如果不是因为电路内的能量损失，这种在电容器C和电感之间来回传递能量的振荡作用将无限期地持续下去。电能在电感线圈的直流或实际电阻、电容器的电介质和电路的辐射中损失，因此振荡稳步下降，直到它们完全消失并且过程停止。

然后在实际的LC电路中，振荡电压的幅度在每个半振荡周期减小，最终将消失为零。然后称振荡为“阻尼”，阻尼量由电路的质量或Q因数决定。

阻尼振荡

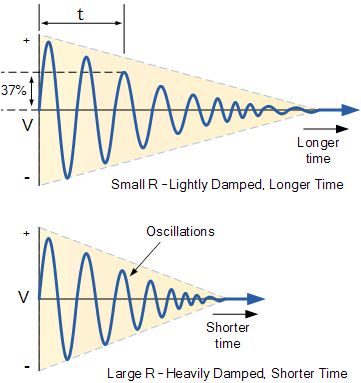
振荡电压的频率取决于LC谐振电路中的电感和电容值。我们现在知道，要在谐振电路中发生共振，必须有一个频率点的值XC，容抗值与XL，感抗（XL=XC），因此将相互抵消，只留下电路中的直流电阻来对抗电流流动。

如果我们现在将电感电感的感抗曲线放在电容器容抗曲线的顶部，使两条曲线位于相同的频率轴上，则交点将给我们谐振频率点（ƒr或ωr），如下所示。

共振频率

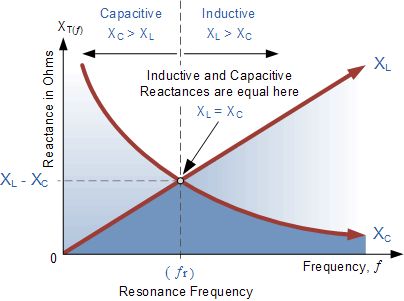
哪里：ƒr在赫兹，L在亨利，C在法拉。

然后，发生这种情况的频率如下：

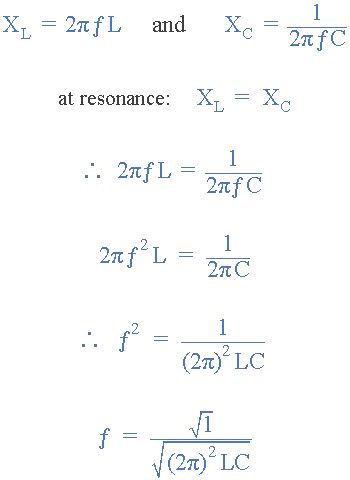
然后通过简化上述方程，我们得到谐振频率的最终方程，ƒr在调谐LC电路中：

LC振荡器的谐振频率

哪里：

L是亨利中的电感

C是以法拉为单位的电容

ƒr是以赫兹为单位的输出频率

该方程表明，如果L或C降低，频率会增加。该输出频率通常缩写为（ƒr）将其标识为“谐振频率”。

为了保持LC谐振电路中的振荡，我们必须替换每次振荡中损失的所有能量，并将这些振荡的幅度保持在恒定水平。因此，更换的能量必须等于每个周期中损失的能量。

如果更换的能量太大，振幅会增加，直到电源轨发生削波。或者，如果替换的能量太小，振幅最终会随着时间的推移降低到零，振荡会停止。

补充这种损失能量的最简单方法是从LC谐振电路中获取部分输出，将其放大，然后再次将其反馈到LC电路中。此过程可以使用使用运算放大器、FET 或双极晶体管作为其有源器件的电压放大器来实现。但是，如果反馈放大器的环路增益太小，则所需的振荡衰减为零，如果太形就会失真。

为了产生恒定的振荡，必须精确控制反馈到LC网络的能量水平。然后，当幅度试图从参考电压向上或向下变化时，必须有某种形式的自动幅度或增益控制。

为了保持稳定的振荡，电路的总增益必须等于1或单位。如果振荡越小，振荡就不会开始或消失到零，振荡就会发生，但幅度会被电源轨削波，从而导致失真。考虑下面的电路。

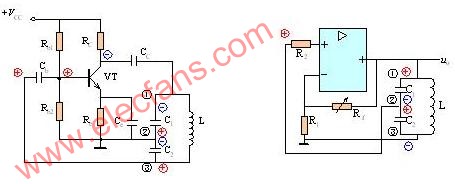
基本晶体管LC振荡器电路

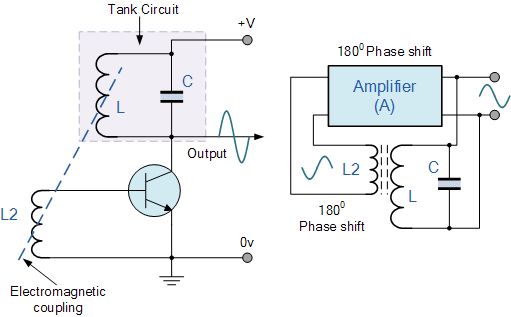
双极晶体管用作LC振荡器放大器，调谐LC谐振电路用作集电极负载。另一个线圈L2连接在晶体管的基极和发射极之间，其电磁场与线圈L的电磁场“相互”耦合。

两个电路之间存在“互感”，一个线圈电路中流动的变化电流通过电磁感应在另一个线圈电路中感应出电位电压（变压器效应），因此当调谐电路中发生振荡时，电磁能量从线圈L传递到线圈L2，并在晶体管的基极和发射极之间施加与调谐电路中相同频率的电压。通过这种方式，必要的自动反馈电压被施加到放大晶体管上。

通过改变两个线圈L和L2之间的耦合，可以增加或减少反馈量。当电路振荡时，其阻抗为阻性，集电极和基极电压为180o异相。为了保持振荡（称为频率稳定性），施加到调谐电路的电压必须与调谐电路中发生的振荡“同相”。

因此，我们必须引入额外的180o相移到集电极和基极之间的反馈路径。这是通过将L2的线圈绕绕在相对于线圈L的正确方向上，为振荡器电路提供正确的幅度和相位关系，或者通过在放大器的输出和输入之间连接相移网络来实现的。

因此，LC振荡器是“正弦振荡器”或更常见的“谐波振荡器”。LC振荡器可以产生高频正弦波，用于射频（RF）型应用，晶体管放大器为双极晶体管或FET。

谐波振荡器有许多不同的形式，因为有许多不同的方法来构建LC滤波器网络和放大器，最常见的是HartleyLC振荡器，Colpitts LC振荡器，阿姆斯特朗振荡器和Clapp振荡器等等。

LC 振荡器示例 No1

将200mH的电感和10pF的电容器并联在一起，形成LC振荡器谐振电路。计算振荡频率。

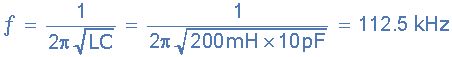
那么从上面的例子中我们可以看出，通过减小电容C或电感的值，L将具有增加LC谐振电路振荡频率的效果。

LC 振荡器摘要

LC振荡器谐振电路所需的基本条件如下。

要使振荡存在振荡，振荡器电路必须包含无功（频率相关）组件，即“电感器”、“L”或“电容器”、“（C）”以及直流电源。

在简单的电感电容LC电路中，由于元件和电路损耗，振荡会随着时间的推移而衰减。

需要电压放大来克服这些电路损耗并提供正增益。

放大器的总增益必须大于1，单位。

通过将部分输出电压反馈到幅度和同相正确的调谐电路（0o).

振荡只有在反馈为“正”（自我再生）时才会发生。

电路的总相移必须为零或360o这样来自反馈网络的输出信号将与输入信号“同相”。

在下一个关于振荡器的教程中，我们将研究最常见的LC振荡器电路之一的操作，该电路使用两个电感线圈在其谐振电路中形成中心抽头电感。这种类型的LC振荡器电路通常被称为哈特利振荡器。

审核编辑：汤梓红