受限水声阵列阵型定位算法比较研究

摘要：空气信道中的阵列信号处理技术可以进行多个目标同时定位，经过适配后应用在水下信道中，可以实现水声定位。空间信号到达方向是阵列信号处理的重要环节，利用特征结构的子空间方法确定相同范围内一个或多个信号源的空间地理位置，常用的方法是 MUSIC 算法和 ESPRIT算法。在工程实践中，多个阵元仅有有限路信号采集通道形成受限水声阵列，在受限水声阵列条件下，如何选取阵型，匹配相应算法，对水声定位结果至关重要。选择二维面阵，包括 L 阵型、双 L 阵型、均匀面阵型、“口”字阵型，用数据进行仿真验证，分析比较定位效果，结果表明不同阵型匹配相应算法，在定位精度或计算速度方面各有优缺点。针对不同工程需求，可以选取相应的阵型，对实践提供了有效的参考依据。

0 引 言

常规的水声定位系统一般利用时间差或者相位差的方法，一次只能完成一个目标的水下定位，无法实现在同一场景中同时定位多个目标。受到空气信道中的阵列信号处理技术可以进行多个目标同时定位的启发，经过适配后应用在水下信道中，就可以解决此问题。空气信道无线电阵列信号处理技术历经多年的发展，技术已经非常成熟，并且应用广泛，比如在雷达、导航、通信等领域[1]，阵列信号处理技术就是其中应用比较频繁和成 熟 的 一 种 。空 间 信 号 到 达 的 方 向（Direction ofArrival，DOA）是呈现在阵列信号处理过程中的一个重要环节，目标是确定在相同范围内一个或者多个信号源的空间地理位置。DOA 估计算法采用了特征结构的子空间方法，对数个空间信号到达的方向进行研究，满足用户需求，其分辨率的大小由瑞利限决定，也就是阵列长度及其间隔[2]。出现在超分辨率 DOA 估计算法中最早的两种著名算法分别是 MUSIC 算法（及改进算法）和ESPRIT 算法，将空间谱估计技术向高分辨侧技术推进，并且有了长足发展。

选择匹配的阵列信号模型是阵列信号处理之前最关键的步骤。本文选择了多个二维面阵模型，用 DOA估计算法分别加以验证，从不同方面进行比较，给用户提供客观评价，方便在水声定位工程实践中选择合适的信号处理方法。

1 受限水声阵列

水声定位系统硬件由多阵元水听器阵列组成，后续没有完成多路水声信道建设，仅有有限路采集通道，形成了一种受限的水声阵列阵型。为完成多目标定位，在硬件基础上增加了通道选择模块，用来快速实现阵型变换。模块采用 FPGA 芯片，采用 Verilog HDL 语言编写代码，设置阵型选择模式，每个模式可以代表下文中所选的对应阵型。用运算放大器对采集到的模拟信号完成放大后，采用带通滤波选择相同的通带频率和工作频率，保障各个信号通道基础信息设置一致[3⁃4]。

2 二维面阵模型

为了简化分析，更快速准确地得到仿真结论，假设采用的信号源形式为：点辐射源、窄带信号，假定噪声为高斯白噪声，并且与信号源不相关，信号源的数量是已知的，也可以从计算中获取，接收阵列与信号源之间是远场环境。本文中应用的二维面阵有 L 阵型、双 L 阵型、均匀面阵型、“口”字阵型，信源至阵列的俯仰角 θ 定义为原点到信源的方向矢量与 z 轴方向矢量间的夹角，方位角 ϕ 则是原点到信源的方向矢量在 x⁃y平面上的投影与 x 轴方向矢量之间的夹角[5]。信源与接收阵之间满足远场条件，故用一点表示整个阵列。L 阵型有 M + N - 1 个阵元，由 x 轴上 N 个阵元和 y轴上 M 个阵元均匀构成，阵元间距为 d。假设有 K 个信源，其 DOA 为 ( θk ,ϕk（)k=1，2，…，K），其中 θk，ϕk 分别为第 k个信源的俯仰角和方位角。

双 L阵型类似于 L阵型，结构图如图 1所示。

对于均匀面阵型，结构图如图 2 所示，阵元数为M × N，均匀分布在平面上。信源数为 K，θk，ϕk 分别代表第 k个信源的俯仰角和方位角。

“口”字阵型即由 4 条线阵围成一个矩形，方向矩阵雷同于双 L阵型。

3 不同算法匹配阵型仿真比较

二维 DOA 估计本文采用 L 阵型、双 L 阵型、均匀面阵型和“口”字阵型实现二维参数估计，多数二维 DOA算法是在一维 DOA 算法基础上针对二维空间提出的改进或推广方法[6]。二维 MUSIC 算法是二维 DOA 估计的典型算法。本文针对不同阵型选用不同适配算法：二维MUSIC、求根 MUSIC、ESPRIT 和降维 MUSIC 算法定义均方根误差为[7]：

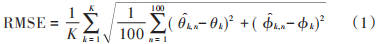
式中 θk, n 和 ϕk, n 分别表示第n次蒙特卡洛仿真中的θk 和ϕk的估计值。

3.1 L阵型⁃MUSIC 和求根 MUSIC 算法

不同于一般两边等阵元数的 L 阵型，由于硬件限制，y 轴方向只有4 个阵元，x 轴就会有 9 个阵元，阵元数的不同使得两个角度的测量误差水平不同。2D⁃MUSIC算法利用空间谱函数进行二维的谱峰搜索，是一个经典的算法，具有普遍适用性，缺陷就是要进行空间二维角度搜索，运行时间长。求根 MUSIC 算法用多项式求根的方法代替谱搜索，能大大降低运算量[8]。

仿真条件：L 阵型，x 轴上有 9 个阵元，y 轴上有 4 个阵元，公用参考点阵元，假设 3个信号互不相干，角度[7]分别为（10°，20°），（30°，40°），（50°，70°），信噪比选用0 dB，5 dB，10 dB，15 dB，20 dB 和 25 dB。使用 MUSIC 和求根 MUSIC 算法，MUSIC 算法取 1°作为搜索步长。蒙特卡洛次数为 100，图 3、图 4 分别为 MUSIC 单次运算图和求根 MUSIC 算法估计性能图，信噪比均为 10 dB，快拍数为 200。

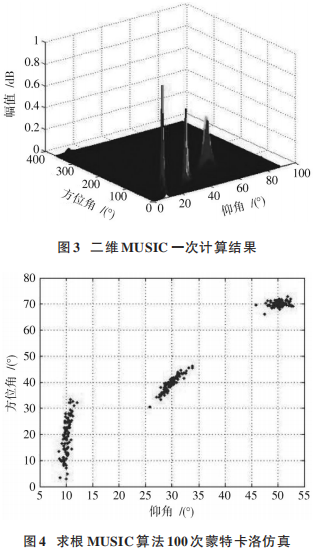
从图 3、图 4 可以看出，MUSIC 算法尖峰还是很明显，求根 MUSIC 在低仰角时方位角误差很大，甚至大于10°。在快拍数为 200，不同信噪比下，各算法均方根误差对比如表 1所示。

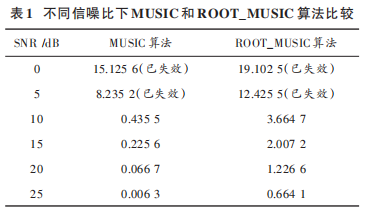
MUSIC 算法平均运算时间为 1.181 1 s，求根 MUSIC算法平均运算时间为 0.093 7 s。由表 1 可以分析出求根 MUSIC 算法由于不需要全空间搜索，所以计算时间短许多，但由于 y 轴上阵元数限制，均方根误差偏大。MUSIC 算法运算时间过长，不适合实时运算，但精度高，适合事后回放。两种算法均只能在信噪比大于 10 dB下才能发挥作用。

3.2 双 L阵型⁃MUSIC 算法

双 L 阵型呈 U 型，x 轴上有 6 个阵元，y 轴上有 2 组，每组 4 个阵元，公用参考点阵元，假设 3 个信号互不相干，角度分别为（10°，20°），（30°，40°），（50°，70°），信噪比 选 用 0 dB，5 dB，10 dB，15 dB，20 dB 和 25 dB。MUSIC 算法取 1°作为搜索步长，蒙特卡洛次数为 100。

在快拍数为 200，不同信噪比下，MUSIC 算法均方根误差对比如表 2所示。

MUSIC 算法平均用时 2.743 9 s。原先考虑使用求根 MUSIC 算法作为比较，但仿真后发现 y 轴上 4 个阵元大大限制了该算法，使得求根 MUSIC算法经常得出错误的结果，因此不将求根MUSIC算法作为L阵型的比较。

3.3 均匀面阵型⁃MUSIC、降维 MUSIC 和 ESPRIT算法

由于测量通道有限，不能利用全部阵元，所以选取3×4 均匀面阵型作为比较对象，由于求根 MUSIC 算法对x 轴和 y 轴上阵元数量敏感，所以此次面阵算法采用MUSIC、降维 MUSIC 和 Unitary_ESPRIT 算法作为比较。降维算法优点有：可以实现配对的二维角度估计；只需一次一维局部搜索；运算量大大降低；完全利用信号子空间和噪声子空间；角度估计性能非常接近 2D⁃MUSIC算法[9]。Unitary_ESPRIT 算法通过 Q 矩阵，将方向矩阵转变为只有实部，从而降低运算复杂度。角度估计可以根据实部和虚部信息配对好，无需另行计算配对[9]。

仿真条件：均匀面阵型，x轴上有 4个阵元，y轴上有3 个阵元，呈 4×3 排布，假设 3 个信号互不相干，角度分别为（10°，20°），（30°，40°），（50°，70°），信噪比选用0 dB，5 dB，10 dB，15 dB，20 dB 和 25 dB。使用 MUSIC、降 维 MUSIC 和 ESPRIT 算 法 ，MUSIC 算 法 取 1° 作 为搜 索 步 长 ，降 维 MUSIC 选 取 0.001 精 度 作 为 搜 索 步长 。蒙 特卡洛次数为 100。图 5~图 7 分别为 MUSIC、Unitary_ESPRIT 和降维 MUSIC 算法估计性能图，信噪比均为 10 dB，快拍数为 200。

快拍数为 200，不同信噪比下各算法均方根误差比较如表 3所示。

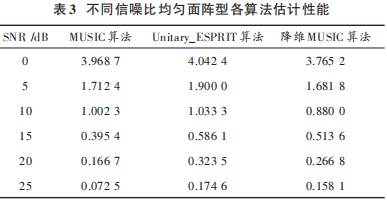
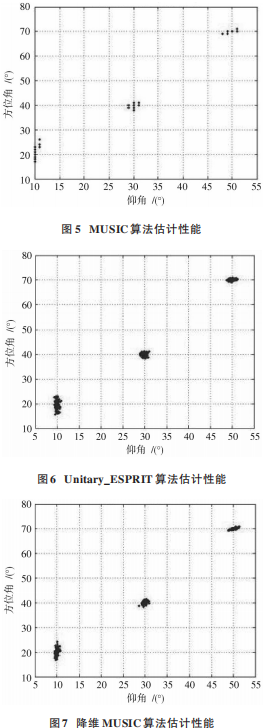
MUSIC 算 法 平 均 运 算 时 间 为 3.442 1 s，Unitary_ESPRIT 算法平均运算时间为 0.001 4 s，降维MUSIC 算法平均运算时间为 0.196 0 s。由表 3 可以分析出，MUSIC 算法精度高，但由于需要进行二维角度搜索，运算量很大，运算时间过长，不适合作为实时定位算法，而 Unitary_ESPRIT 通过 Q 矩阵，将方向矩阵转变为只有实部，从而降低运算复杂度，并且根据实部虚部信息获得配对好的角度估计[10]。降维 MUSIC 算法计算精度和搜索步长有关，类似于MUSIC算法，但只有一维搜索，所以计算总量相较MUSIC减少很多，高于Unitary_ESPRIT算法。

3.4 “口”字阵型⁃MUSIC 算法

“口”字阵型每边为 4 个阵元，呈正方形排布，假设3 个信号互不相干，角度分别为（10°，20°），（30°，40°），（50°，70°），信噪比选用 0dB、5 dB、10 dB、15 dB、20 dB和 25 dB。MUSIC 算法取 1°作为搜索步长。蒙特卡洛次数为 100，快拍数为 200，不同信噪比下 MUSIC 算法均方根误差比较如表 4所示。

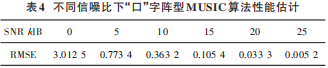
MUSIC 算法平均运算时间为 2.945 5 s。这种非常规阵型适配算法只能使用 MUSIC 算法。

3.5 二维面阵阵型适应算法比较

以上分小节介绍了各阵型组成及各阵型下不同算法性能，在快拍数为 200，不同信噪比下综合各阵型各算法均方根误差结果如图 8 所示，各阵型算法用时如图 9所示。

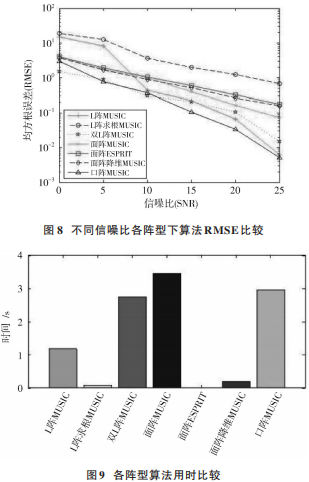
从图 8可以得出以下结论：

1）“口”字阵型 MUSIC 算法和双 L 阵 MUSIC 算法在所比较的各阵型算法中均方根误差最优，这与该两种阵型所围成的面积最大有关；

2）均匀面阵型三种算法没有表现很大的差距；

3）求根 MUSIC 在各阵型中表现不佳，甚至在其他阵型下无法计算出正确的结果，这与 y 轴最多只有 4 个阵元有很大的关系。

由图 9 可以看出，面阵 MUSIC 算法用时最长，因为每 次 循 环 均 会 计 算 Kronecker 积 ，所 以 较 其 他 阵 型MUSIC 用时较长。均匀面阵型 ESPRIT 用时最短，可达毫秒级，求根 MUSIC 和降维 MUSIC 算法用时大幅低于MUSIC 算法。综合各算法均方根误差，MUSIC 算法精度高、用时最长，不适合实时计算，可用于事后数据分析，使 用 更 高 性 能 计 算 机 提 高 计 算 速 度 。 L 型 阵 求 根MUSIC 是精度最差的，面阵 ESPRIT 和降维 MUSIC 计算精度相差不大，所以选取运行时间更短的面阵 ESPRIT算法作为系统实时定位算法，相对应的系统阵型为 4×3均匀面阵型。

综合以上仿真可得出结论：当信号源深度不定时，可采用均匀面阵型的形式，使用 ESPRIT 算法实时解算仰角和方位角。当需要更高精度和不需要实时计算时，可采用“口”字阵型列采集数据，使用更快计算速度的计算机，采用 MUSIC 算法进行更高精度解算。

4 结 论

本文分别采用二维 MUSIC、求根 MUSIC、ESPRIT 和降维 MUSIC 算法，选取合适的二维面阵阵型，进行二维DOA 估计，用仿真数据加以验证，对比不同算法匹配相应阵型各自的优缺点，在实用性、计算优势和定位精度上各有不同，用户在使用时可以根据实际情况选择最佳方案。

审核编辑 ：李倩