PID控制算法基本原理

大家好，我是ST。

今天和大家聊一聊PID算法的控制原理。

在讲解PID算法之前，在此抛出一个问题，如何通过算法控制加热器使水温稳定在50摄氏度?

一、传统的位式控制算法(非PID算法)

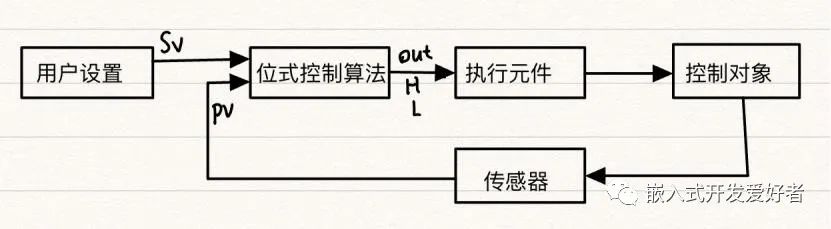
(1)算法逻辑:用户设置目标温度Sv为50，传感器检测控制对象即水的温度Pv

①当Pv ②当Pv==SV时，表示实际温度等于目标温度，不输出

③当Pv>Sv时，表示实际温度高于目标温度，输出低电平OUT=L，让执行元件即加热器不工作，即0功率输出

(2)代码实现:

#define Sv 50
void func(unsigned int Pv)
{
          if(Pv

(1)缺点

①控制算法过于简单，单纯对设定值和输出值进行比较，一旦发现低于设定值，就输出高，否则就输出低

②要么处于全功率下，要么处于0功率下工作

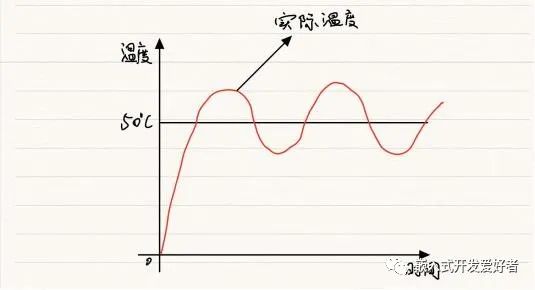
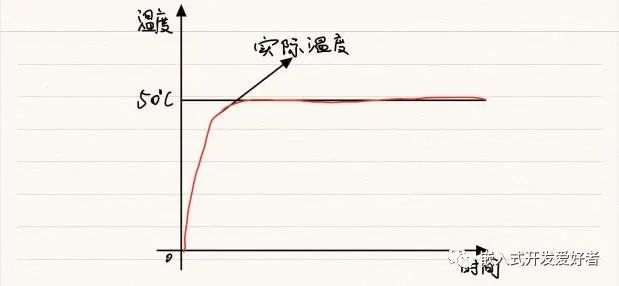
③会导致温度总是在设定值上下波动如下图所示，因为控制对象具有一定的惯性，即加热时水的温度不会立即上升，不加热时水的温度不会立即下降

二、PID闭环控制

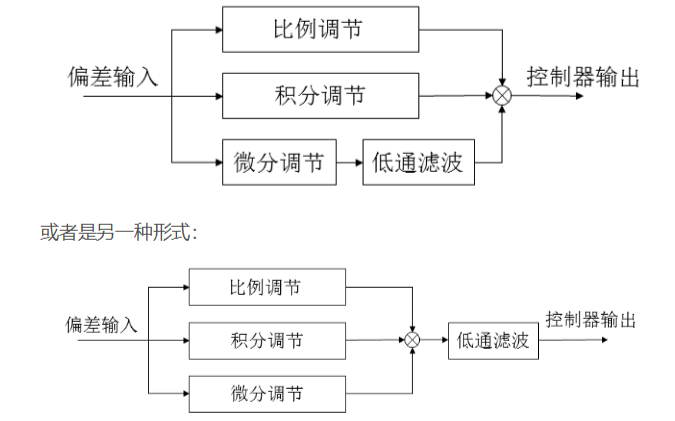
PID闭环即比例-积分-微分控制，即通过对偏差进行比例-积分-微分控制，使得当前值趋于目标值的过程。一般来说，比例P控制是必须的，所以衍生出很多组合的PID控制，如PD、PI、PID。离散PID公示为：

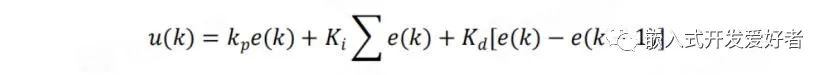
其中，e(k):为k时刻的偏差，u(k):为输出的控制量(对于加热器来说是PWM)

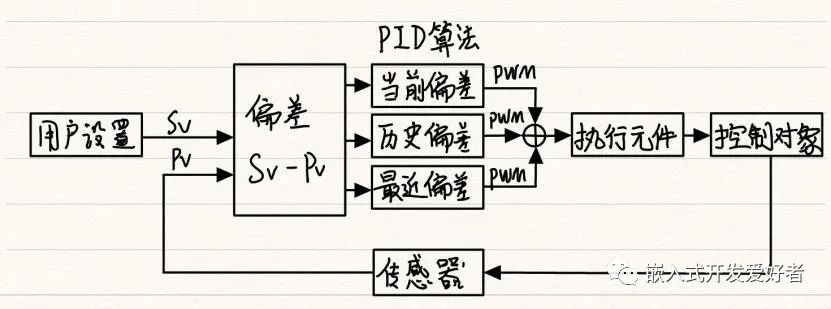
(1)比例控制(P)

Sv为用户设置目标值，Pv为控制对象即水的当前温度值

Ek为目标温度与当前温度的偏差：Ek=Sv-Pv

①当Ek<0时，表示当前温度未达标

②当Ek==0时，表示当前温度正好达标

③当Ek>0时，表示当前温度已超标

比例控制算法公式：PWM=Kp*Ek

Kp参数的解释：Kp可以理解为一个衰减器或者放大器，主要是用来调整偏差值，调整其增益或者说是放大倍数

比例控制的作用：

调节到达目标值的时间，增大Kp会增加相应速度，但可能会造成超调，有静态误差

(2)积分控制(I)

Ek为历史上某一时刻的偏差，Sk为历史偏差之和:Sk=E1+E2+E3+...+EN ①当Sk<0时，表示历史上大部分时间温度未达标(现在是否达标不知道) ②当Sk==0时，表示历史上温度总体上是好的(现在温度是否达标不管) ③当Sk>0时，表示历史上大部分时间温度超标(现在温度是否超标不知道)

积分控制公式：

PWM=Ki*Sk Ki参数的解释：Ki可以理解为一个衰减器或者放大器，主要是用来调整Sk，调整其增益或者说是放大倍数

比例控制的作用：

如果我们把加热器放到一个非常冷的地方对水进行加热，加热目标值是50摄氏度在比例控制下，水温度慢慢升高，直到升高到45摄氏度，发现天气太冷，水散热的速度正好等于比例控制下的加热速度。所以水温永远停留在45摄氏度，永远到不了50摄氏度。如果加上积分控制，只要没有达到50摄氏度，就会存在偏差，这时候对偏差不断积分(累加)，输出的PWM就会增大，即增大的加热器的功率，使水温能达到50摄氏度。所以比例控制的作用是，减少静态情况下的误差，但容易造成震荡

(3)微分控制(D)

E(k)为当前偏差值，E(k-1)为上一次偏差值 Dk为最近两次偏差相减，表示最近两个时间点偏差的变化：Dk=E(k)-E(k-1) ①当Dk<0时，表示偏差有增大的趋势 ②当Dk==0时，表示偏差稳定，输出为0 ③当Dk>0时，表示偏差有减小的趋势

微分控制公式：

PWM=Kd*Dk Kd参数的解释：Kd可以理解为一个衰减器或者放大器，主要是用来调整Dk，调整其增益或者说是放大倍数

微分控制的作用：

只要物理量存在变化，微分控制就会起作用，让物理量的变化速度趋于0，增大Kd参数能够抑制震荡，尽快稳定，但有可能造成调节周期过长

(4)PID算法控制代码实现

int PID(int Sv,int Pv)
{
      /* Sv：用户设定的目标值
      ** Pv:传感器检测到的当前值
      ** Ek:目标值与当前值的偏差值
      ** last_Ek:上一次的Ek值
      ** Sk:偏差值Ek的积分值
      ** PWM:输出的PWM值
      */
      static int Ek,last_Ek,Sk;
      static float PWM;
      Ek=Sv-Pv;
      Sk+=Ek;
      /*积分限幅，Sk_max和Sk_min根据情况自己给定*/
      if(Sk>Sk_max)   Sk=Sk_max;
      if(SkPWM_max)   PWM=PWM_max;
      if(PWM

当Ek、Ki和Kp参数参数调节的比较好时，温度能及时达到目标温度并且很平稳如图所示：

三、PID控制参数整定的方法

PID控制的调节经验可以总结为：先只使用 P 控制，增大 P 系数直到系统振荡，然后加入微分控制增大阻尼，消除振荡之后再根据系统对响应和静差等具体要求，调节 P 和 I 参数。

例子：我们需要调节目标值为 10390，当前值为 10000

①先设置Kd和Ki的参数值为0，然后把Kp参数从0逐渐增大，直到出现震荡

当Kp=62，Ki=0，Kd=0时，响应曲线如下：

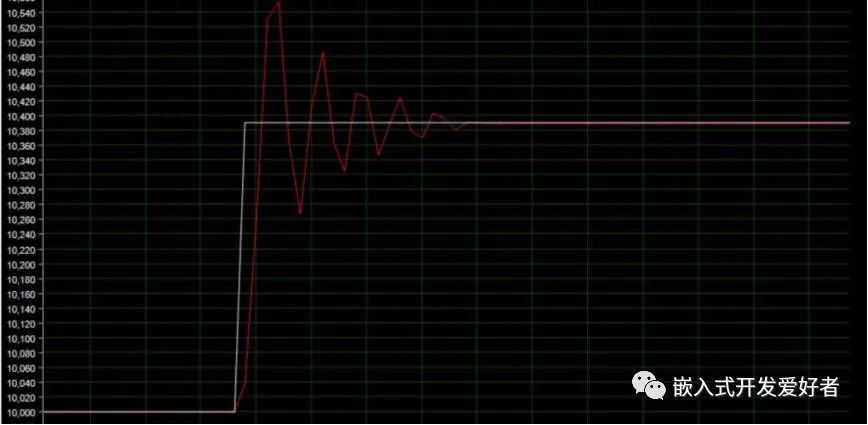
②保持Kp=62，Ki=0不变，Kd从0逐渐增大，当Kd=188时，响应曲线如下：

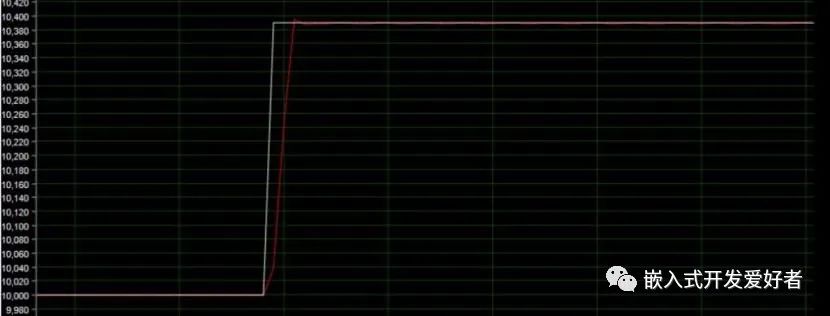
当加入微分控制的时候，可以看到，系统的振荡得到了抑制，但是系统的响应变慢了。因为微分控制相当于一个阻尼力，引入微分控制相当于增大系统的阻尼。这个时候需要结合 KP 和 KI 进行进一步的优化。在实际生产中，需要对不同项目进行评估，比如一个系统对快速性要求不高，但对稳定性和准确性的要求很高，那么就需要严格控制超调量和静差。

总结：PID控制算法是经典控制方法中，现实生活中使用非常广泛，掌握其中的原理非常重要。

审核编辑：汤梓红