傅里叶变换的提出让人们看问题的角度从时域变成了频域,多了一个维度。快速傅里叶变换算法的提出普及了傅里叶变换在工程领域的应用,在科学计算和数字信号处理等领域,离散傅里叶变换(DFT)至今依然是非常有效的工具之一。
比如下图是一个幅度为1、频率为2Hz的正弦波和它的离散傅里叶变换后的结果。
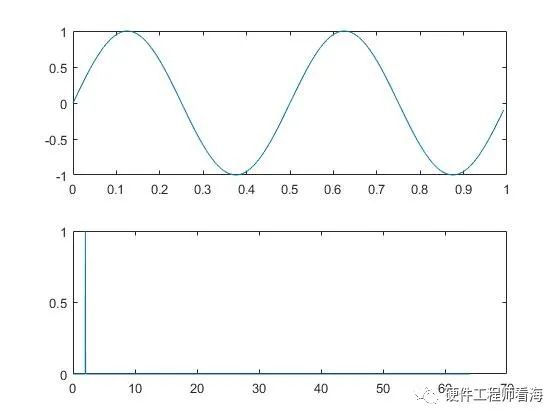
信噪比(SNR)是信号与噪声的比率,它是衡量通信或模拟系统性能的重要指标之一,与傅里叶变换更是有千丝万缕的联系。在很多情况下,我们是通过傅里叶变换来评估信噪比,如果评估方法不对,很难的到我们期望的结果,经常会事与愿违。
求解SNR的过程,我们是用‘评估SNR’来描述,这就是说我们无法精确计算出SNR,只能进行评估,事实也是如此。
评估SNR的方法分为时域和频域两种。我们以一组离散样本点为分析目标,看下如何评估SNR,及其误区。
时域估计SNR
Xs(n)为信号序列,Xn(n)为噪声序列,则信号X(n)=Xs(n)+Xn(n),是一组带噪离散序列,在时域上评估X(n)的信噪比公式如下:
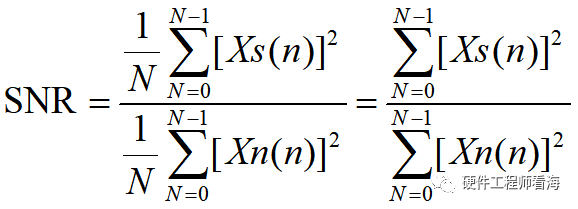
其意义为分别求取离散信号、噪声功率和,计算二者之比。这里有个前提是,我们需要分离出信号与噪声,然后才能求解,
然而问题也在于此,对于一段给定的离散时间序列,我们很难完全分离出信号和噪声,所以时域评估SNR是有局限性的,而且不够直观,所以通常我们在频域下求解。
频域估计SNR
在频域上的SNR计算原理和时域很接近,还是求信号功率与噪声功率只比。最简单的方法是在频谱X(m)上设置阈值,阈值之上为信号,阈值之下为噪声。这样就会有阈值设置带来的估计准确性问题,同时信号频带范围内或多或少也会有噪声叠加进来,在频域计算SNR也是一个近似。

SNR以dB作为单位,SNR(dB)=10*log10(SNR)。
我们往往使用Matlab评估SNR,Matlab是非常强大的数学工具,其集成了SNR计算函数,如果应用不正确,误差会非常大,无法得到预期结果,举例如下。
下图是一个幅度为1、频率为2Hz的正弦波和它的离散傅里叶变换后的结果。

用Matlab SNR函数计算计算信噪比的结果如下,蓝色为感兴趣的信号成分,橙色为噪声。这个频域图就可以表征SNR,橙色的噪声数值越小、越低,说明信噪比越高、越好。即使红色圆圈部分有一点噪声,在评估单频率成分信号的SNR时,这依然是一个非常有效的手段。
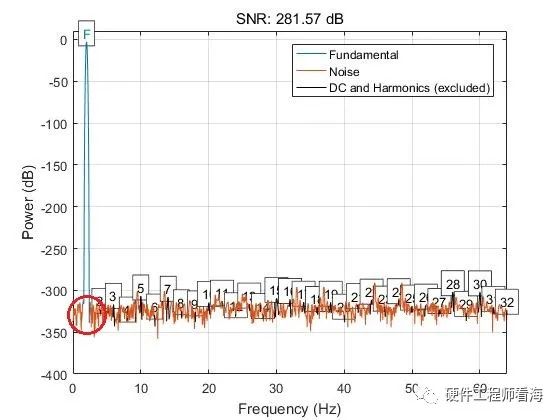
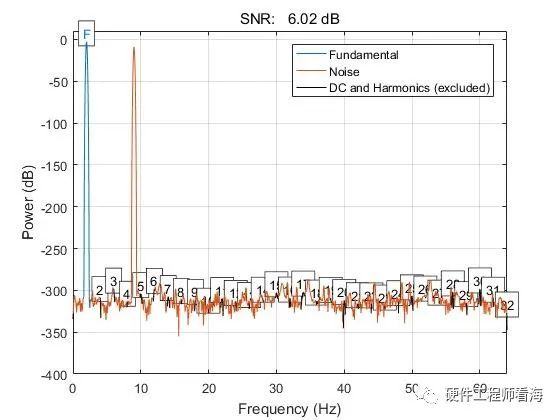
假如一信号x(n)=sin(4pit)+0.5sin(18pi*t),如下图是一个幅度为1、频率为2Hz的正弦波叠加幅度为0.5、频率为9Hz的正弦波的结果。
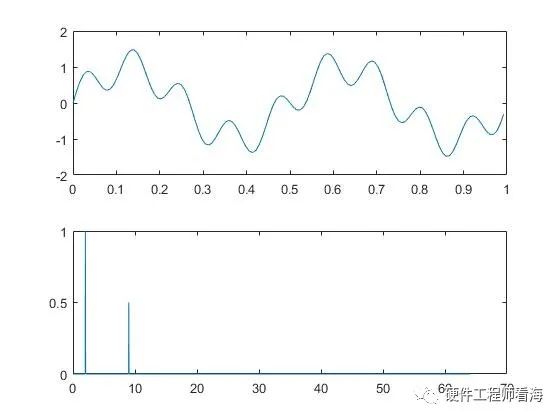
用Matlab SNR函数计算计算信噪比的结果如下,蓝色为感兴趣的信号成分,橙色为噪声,matlab舍弃了频率为9Hz、能量少的成分,只计算了2Hz信号的信噪比。
所以倘若我们的感兴趣信号比较复杂,就不能直接用SNR函数直接计算。
所以我们一定要在理解DFT与SNR关系的基础上,正确使用matlab才能得到期望的SNR结果。
在过采样中,信噪比、ADC有效位数、过采样率是有千丝万缕的联系,了解了基本的概念后,我们一步一步理解过采样的原理。
审核编辑:刘清
-
信噪比
+关注
关注
3文章
253浏览量
28594 -
DFT
+关注
关注
2文章
224浏览量
22680 -
SNR
+关注
关注
3文章
195浏览量
24372 -
傅里叶变换
+关注
关注
6文章
437浏览量
42566
发布评论请先 登录
相关推荐




 通过傅里叶变换来评估信噪比
通过傅里叶变换来评估信噪比












评论