01
研究动机
数学问题(英文叫Math Word Problem,简称MWP)的求解要求给定一段描述文本,其中包含对于若干已知变量和一个未知变量的描述,要求利用变量间的数值关系来推理计算出未知变量的准确数值。
一个具体的例子如下图1所示,可以发现一个数学问题可能对应着多个正确的表达式或二叉树,有着非确定性的输出空间,而目前主流方法输入问题文本序列来学习特定单个表达式序列或二叉树的生成,使得模型所学到的知识不完整,并需要大量数据来提升性能,限制了模型在低资源场景下的表现。
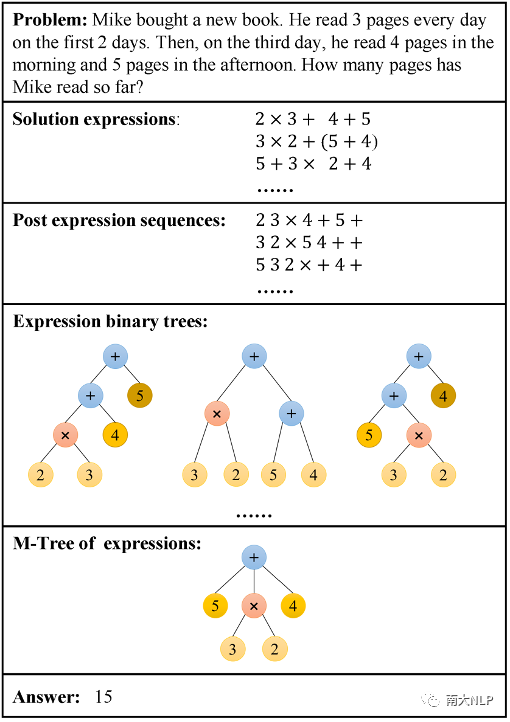
图1: MWP问题示例
对于MWP的输出多样性,分析原因如下:
1、计算顺序的不确定性:a)运算之间常拥有相同的计算优先级。如n1 + n2 + n3 − n4 中的三个运算符优先级一样,可以等价转换为不同的序列或二叉树;b)数学表达式中括号的使用给计算顺序也带来了不确定性。如n1 + n2 − n3, n1 − (n3 − n2) 和 (n1+n2)−n3都是等价的表达;
2、运算的可交换性带来的不确定性:加法和乘法操作两边的算子可以进行交换且不影响计算逻辑与最终结果,使得输出的结构具有多样性的表达,如n1 + n2 × n3可以转换为n1+n3×n2,n2×n3+n1等;
为了解决由多样性给问题求解带来的挑战,我们提出了基于结构统一M叉编码树的数学问题求解器。针对第一点原因,在二叉树的结构基础上,我们设计了拥有任意分支数量的M-tree,在竖直方向上对树的结构进行统一;针对第二点,我们在M-tree中重新定义了新的M元运算,使得所有的运算都满足可交换性,将只在子节点左右顺序不一样的两棵M-tree视为相同的结构,从而在水平方向对树的结构进行统一。
而为了学习输出M-tree,我们放弃了进行自上而下且从左到右的自回归式生成方法,因为该方法不能避免由于子节点左右顺序的变化而带来的输出(one by one)多样性。我们首先对M-tree进行编码,将其转换为M-tree codes形式的等价表达,用于保存M-tree的结构信息,其中每个code对应M-tree中的一个叶子节点,保存从根节点到叶子节点的路径以及叶子节点本身的信息。
通过一个sequence to code(seq2code)模型学习从输入问题文本序列到每个code的映射,以非自回归的方式生成输出。
02
贡献
1、我们分析了MWP中输出多样性的原因,创新地设计了一个基于M树的方案来统一输出结构;
2、我们设计了M-tree codes来等价表示M-tree,并提出了一个seq2code模型来以非自回归的方式生成codes,据我们所知这是第一个利用M-tree codes和seq2code来分析求解MWP的工作;
3、在广泛使用的Math23K和MAWPS数据集上的实验结果表明,SUMC-Solver在同等实验设置下优于以前的方法。尤其是在低资源的情况下,我们的求解器取得了更好的性能表现。
03
解决方案
方法的整体示例及模型框架如下图2所示,下面介绍M-tree,M-tree codes和seq2code模型的设计。
M-tree的设计:M-tree具有两种节点——内部节点和叶子节点,其中内部节点拥有任意M个子分支(M>=1)且对应四种M元运算:{ +,x,x-,+/ },这四种M元运算都具有可交换性,叶子节点有四种:{原始数值v,v的负数,v的倒数,v的倒数的相反数};定义M-tree的根节点为+类型节点,任何两棵仅在子节点左右顺序不一样的M-tree会被视为同一颗。
M-tree codes的设计:由于M-tree中的内部节点可以拥有任意数量的子分支,且兄弟节点在结构上的位置是等价的,所以基于自回归式的生成不能避免由于兄弟节点的顺序在输出端造成的多样性。为了解决这一难题,我们将M-tree的结构信息编码到每个叶子节点中,在M-tree和叶子节点的codes集合之间形成一个映射,这样模型就能以非自回归的方式生成codes。
具体而言,每个叶子节点的M-tree code由两部分组成:一部分保存数值信息,会使用两个二进制位来区分数值的四种形式,另一部分由根节点到当前叶子节点的路径信息构成。
seq2code模型框架:为了验证M-tree和M-tree codes的先进性,我们设计了一个简单的seq2code模型来求解MWP,它将问题文本序列作为其输入,然后输出问题中数值的相应code(以向量表示)。在结合所有的codes以恢复M-tree之后,我们可以计算出问题的最终答案。整个模型由两部分组成:问题编码器和code生成器。a)问题编码器将MWP的单词转化为向量表示,我们的实验中编码器有两种选择:循环神经网络(RNN)编码器或预训练语言模型(PLM)编码器;b)我们使用了一个简单的三层前馈神经网络(FFNN)来作为生成器。
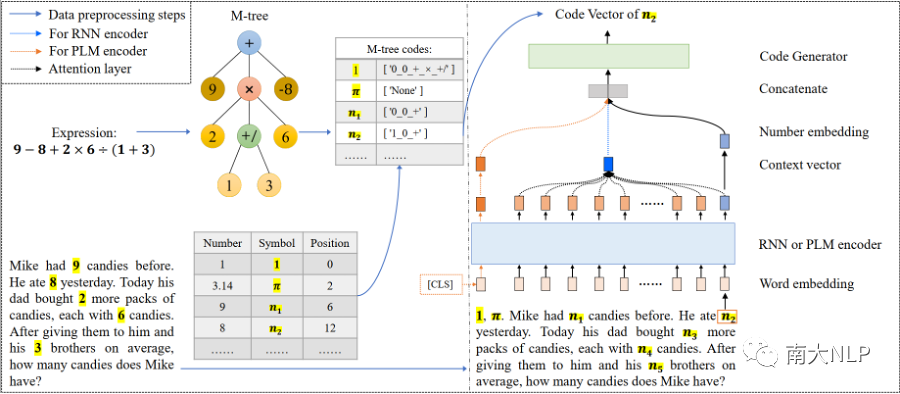 图2: SUMC-Solver问题求解示例与模型框架
图2: SUMC-Solver问题求解示例与模型框架
04
实验
实验结果展示在表1中。SUMC-Solver在两个MWP数据集上的表现优于所有的基准模型。当使用RNN编码器时,SUMC-Solver的准确率比学习表达式序列输出的StackDecoder和T-RNN 高约9-10%。相比学习二叉树输出的方法,SUMC-Solver也取得了比GTS、SAU-Solver和Graph2Tree更好的结果,尽管这些方法使用了精心设计的树解码器或丰富输入表示的图编码器。
当使用预训练语言模型(PLM)作为编码器时,SUMC-Solver达到了82.5%的准确率,比GTS-PLM和UniLM-Solver有了明显的提高(分别为3%和5%)。总之,上述两种不同编码器设置下的结果都表明,M-tree和M-tree codes的设计是合理和先进的,这使得我们只用一个简单的seq2code模型就可以达到更好的性能。
表1:各模型在基准数据集上的性能对比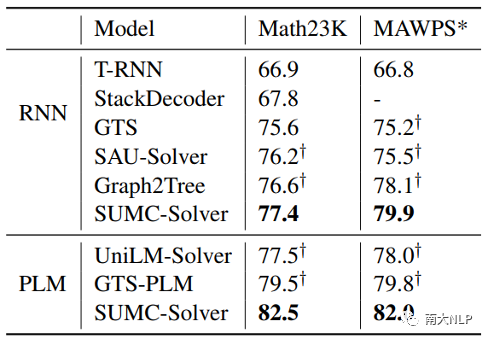
表1中在Math23K数据集上展示的是在公共测试集上的结果,在MAWPS*上展示的是5折交叉验证的结果,带 † 的结果是由我们复现得到的。
MWP的人工标注成本很高,因此提升该模型在低资源场景下的表现是有必要的。我们用不同数据规模的训练集来评估GTS、SAU-Solver和Graph2Tree的性能。测试集统一包含2,312个随机抽样的实例。详细的结果可以在图3中找到。可以看出,无论训练集的大小如何,SUMC-Solver的性能始终优于其他模型。
首先,当训练集的规模小于6000时,SAU-Slover的性能优于GTS;当数量超过6000时,这两个模型的性能相似。就整体性能而言,在资源受限的情况下,SAU-Solver和Graph2Tree的结果比GTS的好。其次,在6000个样本的训练集下,SUMC-Solver和其他模型之间出现了最明显的性能差距,我们的模型在准确率上大约提升了5%。这表明SUMC-Solver在低资源情况下具有突出的优势。
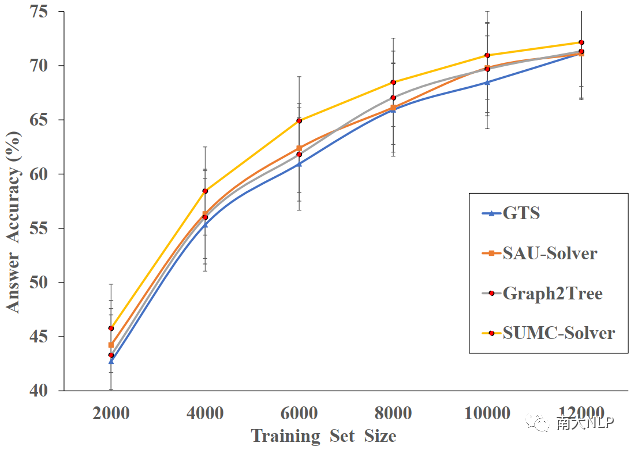
图3:低资源场景下的模型性能对比
此外,我们根据问题计算答案所需的操作数(问题中的某些数值)将测试集(2,312个随机抽样的实例)分为不同的等级,并在不同等级的数据上对比模型性能。详细情况可见图4。从结果中,我们可以看到,大多数的MWP需要2到4个操作数,而SUMC-Slover在需要更多操作数的数据上表现得比基准模型更好,这表明我们的求解器有潜力解决更复杂的问题。
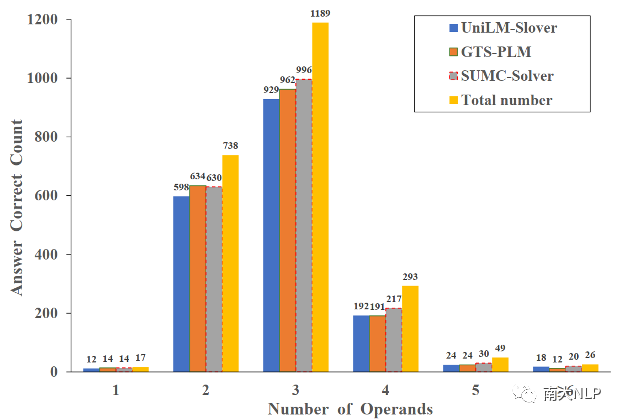
图4:不同模型在需要不同操作数的测试数据上正确回答问题数量的对比
最后,seq2code框架也可以应用于二叉树结构,例如可为每个MWP选择一个二叉树结构的输出,并以同样的方法将其转换为codes。我们对Math23K的训练集数据进行了转换,并对二叉树codes和M-tree codes进行了比较,结果如下表2所示。可以看出,应用M-tree可以大大减少codes集合的大小,并保证得到的codes能够覆盖测试集,这说明M-tree对统一输出结构的效果非常明显。
表2:二叉树与M-tree编码对比
05
总结
针对数学问题求解的输出多样性,我们提出了SUMC-Slover求解器,其应用M-tree来统一多样化的输出,以及seq2code模型来学习M-tree。在广泛使用的MAWPS和Math23K数据集上的实验结果表明,SUMC-Solver在类似的设置下优于目前一些最先进的方法,并且在低资源场景下有着更好的表现。
审核编辑:刘清
-
编码器
+关注
关注
45文章
3658浏览量
134977 -
PLM
+关注
关注
2文章
124浏览量
20887 -
求解器
+关注
关注
0文章
77浏览量
4542
原文标题:EMNLP'22 | 基于结构统一M叉编码树的数学问题求解器
文章出处:【微信号:zenRRan,微信公众号:深度学习自然语言处理】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
一种求解关键路径的新算法
基于四叉树的分形图像编码中的剖分决策函数
基于HBase的四叉树Hilbert索引设计
红黑树(Red Black Tree)是一种自平衡的二叉搜索树




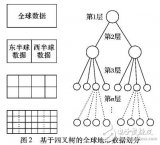
 求一种基于结构统一M叉编码树的求解器解决方案
求一种基于结构统一M叉编码树的求解器解决方案










评论