机器视觉是什么？有哪些技术应用？

提及机器人视觉，不免会想到计算机视觉和机器视觉，很多人会把这三者弄混。

计算机视觉是以图片认知为基础的科学，只通过图片识别输出结果，代表企业是谷歌。

机器视觉多用于生产线上的质量检测，普遍基于2D识别，被广泛应用于3C电子行业，代表企业是康耐视。

机器人视觉是指不仅要把视觉信息作为输入，而且还要对这些信息进行处理，进而提取出有用的信息提供给机器人。是为了让机器人真正变成“机器人”，而不是机器臂。

（一）

传统的机器臂只是自动化设备，是通过编程处理固定的动作，是不能处理具有变动性事物的能力。机器人视觉这要求机器人要拥有3D视觉，能处理三维空间里的三维物体问题，并且具有复杂算法，支撑机器人对位置、动作、轨迹等复杂信息的捕捉，这必须要依赖人工智能和深度学习来完成。

机器人视觉是为认知机器人服务，具备不断学习的功能尤为关键，无论是做检测还是定位引导，当机器人做的次数越多，伴随着数据的增长变化，机器人的准确性也会越高，这跟人的学习成长能力是类似的。

机器人视觉是一种处理问题的研究手段。经过长时间的发展，机器人视觉在定位，识别，检测等多个方面发展出来各种方法。其以常见的相机作为工具，以图像作为处理媒介，获取环境信息。

1、相机模型

相机是机器人视觉的主要武器，也是机器人视觉和环境进行通信的媒介。相机的数学模型为小孔模型，其核心在于相似三角形的求解。其中有三个值得关注的地方： 1.11/f = 1/a + 1/b

焦距等于物距加上像距。此为成像定理，满足此条件时才能成清晰的像。 1.2X = x * f/Z

如果连续改变焦距f ，并同时移动相机改变Z，则可以使得物体x在图像上所占像素数目不变（X）。此为DollyZoom原理。如果某个物体在该物体后方（更大的Z），可利用此原理任意调整两个物体在相片上的比例。 1.3

焦距越长，则视场越小，可以将远处的物体拍清晰。同时相片会有更大的景深。

2、消失点

消失点是相片中特有的。此点在相片中不直接存在，在现实中直接不存在。由于射影变换，相片中原本平行的线会有相交的趋势。如果求的平行直线在图像中的交点，则该点对应现实中无穷远处的一点。该点的图像坐标为［X1 X1 1］。此点成为消失点。相机光心与消失点的连线指向消失点在摄像机坐标系中的方向。

此外，同一平面上各个方向的消失点，会在图像中组成一条直线，称为水平线。该原理可以用于测量站在地上的人的高度。值得注意的是只有相机水平时，horizen的高度才是camera Height.

2.1 位姿估计

如果我们能获得一幅图中的2个消失点。且这2个消失点所对应的方向是相互垂直的（网格），那么我们就可以估计出相机相对于此图像的姿态（靶标位姿估计）。 在获得相机相对于靶标的旋转向量后，如果相机内部参数已知，且已知射影变换矩阵，则可计算相机相对于靶标的距离，那么可以估计机器人的位置。H = K^-1*（H射影矩阵）

2.2 点线对偶

p1×p2 = L12 L12×L23 = p2

3、射影变换

射影变化是空间中平面---》平面的一种变换。对齐次坐标，任意可逆矩阵H均表达了射影变换。简而言之，可以表达为A = HB ，其中AB是［X Y 1］形式的其次坐标。射影变换的一大作用就是将某一形状投射成其他形状。比如，制作相片中的广告牌，或者比赛转播中的广告牌，或者游泳比赛运动员到达后那个biu的一下出现的国旗。射影变换也是增强现实技术的基础。

射影变换的核心在于H的求取。普通的求解方法见机器视觉教材。

假设平面相片的四个点分别是A（0，0，1），B（0，1，1），C（1，1，1），D（1，0，1）。显然，这四个点需要投射到四个我们已知像素位坐标的图像区域中。

此外，我们还可以依据像素位置计算两个有趣的点，V1（x1， y1， z1），V2（x2，y2，z2），这两个点都是图像点。他们对应的实际坐标假设是（0，1，0），（1，0，0）。那么我们就有三个很有趣的实际点了。分别是（1，0，0），（0，1，0），（0，0，1），恰好是一个Identity Matrix。这三个实际坐标经过射影变换会得到像素坐标。像素坐标又是已知的。那么H的第一列就应该对应beta*V2，第二列应该对应alpha*V1。

第三列应该对应gama*【A的像素坐标】。alpha beta gama是常数。【射影变化后的坐标应为常数乘以其次坐标】。

如果能解得alpha beta gama，那么我们就获得了射影变换矩阵。显然把C点的像素坐标带入方程，我们则有3个方程，4个未知数（引入了一个lamda）。但是lamda并不影响，除过去后我们只要

alpha/lamda，beta/lamda，gama/lamda当作未知数即可解除射影矩阵。

所以，射影变换矩阵的第一列代表消失点V1，第二列代表消失点V2，第一列与第二列的叉乘，代表水平线方程（点线对偶）。

（二）

上回介绍了机器人视觉的一些基础信息，说到机器人视觉的核心任务是estimation，理论框架是射影几何理论。然而，整个estimation的首要条件是已知像素点坐标，尤其是多幅图中对应点的像素坐标。 单幅图像的处理方法不赘述，想讲讲不变点检测与不变特征。由于机器人在不断运动，所以可能从不同方向对同一物体进行拍摄。而拍摄的距离有远近，角度有titled. 由于射影变换本身的性质，无法保证两幅图中的物体看上去一样。所以我们需要一种特征提取方法（特征点检测），能够保证检测是旋转，缩放不变的。除此之外还要一种特征描述方法，同样对旋转和缩放不变。

1、SIFT特征提取

SIFT特征提取可以分为以下几个步骤：（1）多尺度卷积；（2）构造金字塔；（3）3D非极大值抑制。

多尺度卷积的作用是构造一个由近及远的图像。金字塔则由下采样进行构造。

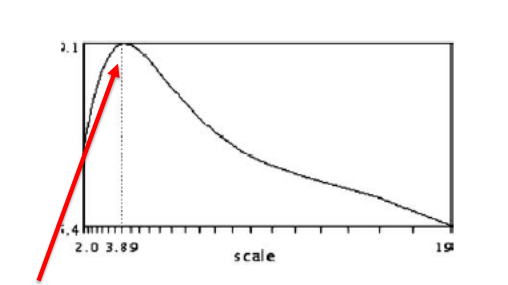
对于不同尺度的图像同一个像素，我们可以跟踪它“灰度”的变化。我们发现，如果某一点对不同 sigma 的模版响应是不同的，最大响应（卷积后的灰度）所对应的scale 成为该点本征scale。这有点像对一个机械结构给不同频率的激励，某一频率下会发生共振，我们可以记录此频率一定程度上代表了此结构（单摆频率只和ml有关，有了f就可以重现系统）。 所以，我们只要找到一个合适的模版（激励方式），再找到最大响应，就可以获取图片中各个点的 Intrinsic Scale（本征尺度）。同一物体在不同距离拍摄后，都会统一在Intrinsic Scale下进行响应。由此解决了尺度不变的问题。 3D非极大值抑制是指在某点的3*3*3邻域内，仅取最大响应，作为特征点。由于该点是空间邻域中响应最强的，所以该点也是旋转不变的。从各个方向看，该点响应最强。

2、SIFT特征描述

特征提取和特征描述实际上是两码事。在上一节中特征提取已经结束了。假如有两幅图片，那么相同的特征点肯定会被找到。特征描述的作用是为匹配做准备，其以特征点局部区域信息为标准，将两幅图中相同的特征点联系起来。特征的本质是一个高维向量。要求尺度不变，旋转不变。

这里所使用的是HOG特征。特征描述可以分为两步：（1）局部主方向确定；（2）计算梯度直方图。 以sigma作为特征描述选择范围是一个合理的想法，因为sigma描述了尺度，特征点位置+尺度 = 特征点所代局部信息。在此基础上，统计其领域内所有像素的梯度方向，以方向统计直方图作为特征向量，至此完成HOG特征构造。重要的是，在统计方向之前，需要把图像主方向和X轴方向对齐。示意图如下：

图中黄色的有点像时钟的东西是特征点+scale，指针代表该片小图像的主方向（PCA）。绿色的是直方图的bin，用于计算特征向量。 最后，我们只要匹配特征向量就可以得到 图像1 --- 图像2 的对应点对，通过单应矩阵的计算就可以将两幅图拼接在一起。如果已知标定信息则可进行3D reconstruction。 （三）上篇文章说到从场景中提取特征点，并且对不同角度中的特征点进行匹配。这次要先介绍一个工具 —— 拟合。 拟合本质上是一个优化问题，对于优化问题，最基本的是线性最小二乘法。换言之，我们需要保证拟合误差最小。

1、最小二乘法拟合

基本的最小二乘法拟合解决的是 点 --- 模型 的拟合问题。以点到直线的拟合为例，按照拟合误差的建模，该问题可以分为两类。

第一类以 因变量 误差作为优化目标，该类问题往往是自变量---因变量模式，xy的单位不同。 第二类以 距离 作为优化目标，该类问题xy的单位往往相同，直线不代表趋势，而是一种几何模型。 由于优化目标不同，故建模方式与解均不同，但是解法思路是一样的，都是讲求和化作向量的模。而向量又是矩阵的运算结果，最终化为奇异值分解问题。

2、RASAC拟合

RanSaC算法（随机采样一致）原本是用于数据处理的一种经典算法，其作用是在大量噪声情况下，提取物体中特定的成分。下图是对RanSaC算法效果的说明。图中有一些点显然是满足某条直线的，另外有一团点是纯噪声。目的是在大量噪声的情况下找到直线方程，此时噪声数据量是直线的3倍。

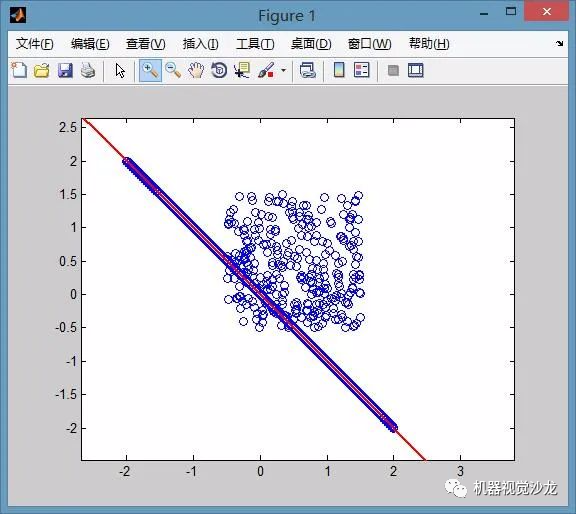
如果用最小二乘法是无法得到这样的效果的，直线大约会在图中直线偏上一点。关于随机采样一致性算法的原理，在wiki百科上讲的很清楚，甚至给出了伪代码和matlab，C代码，想换一个不那么严肃或者说不那么学术的方式来解释这个算法。 实际上这个算法就是从一堆数据里挑出自己最心仪的数据。所谓心仪当然是有个标准（目标的形式：满足直线方程？满足圆方程？以及能容忍的误差e）。平面中确定一条直线需要2点，确定一个圆则需要3点。随机采样算法，其实就和小女生找男朋友差不多。

从人群中随便找个男生，看看他条件怎么样，然后和他谈恋爱，（平面中随机找两个点，拟合一条直线，并计算在容忍误差e中有多少点满足这条直线）

第二天，再重新找个男生，看看他条件怎么样，和男朋友比比，如果更好就换新的（重新随机选两点，拟合直线，看看这条直线是不是能容忍更多的点，如果是则记此直线为结果）

第三天，重复第二天的行为（循环迭代）

终于到了某个年龄，和现在的男朋友结婚（迭代结束，记录当前结果）

显然，如果一个女生按照上面的方法找男朋友，最后一定会嫁一个好的（我们会得到心仪的分割结果）。只要这个模型在直观上存在，该算法就一定有机会把它找到。优点是噪声可以分布的任意广，噪声可以远大于模型信息。 这个算法有两个缺点，第一，必须先指定一个合适的容忍误差e。第二，必须指定迭代次数作为收敛条件。 综合以上特性，本算法非常适合从杂乱点云中检测某些具有特殊外形的物体。

3、非线性拟合

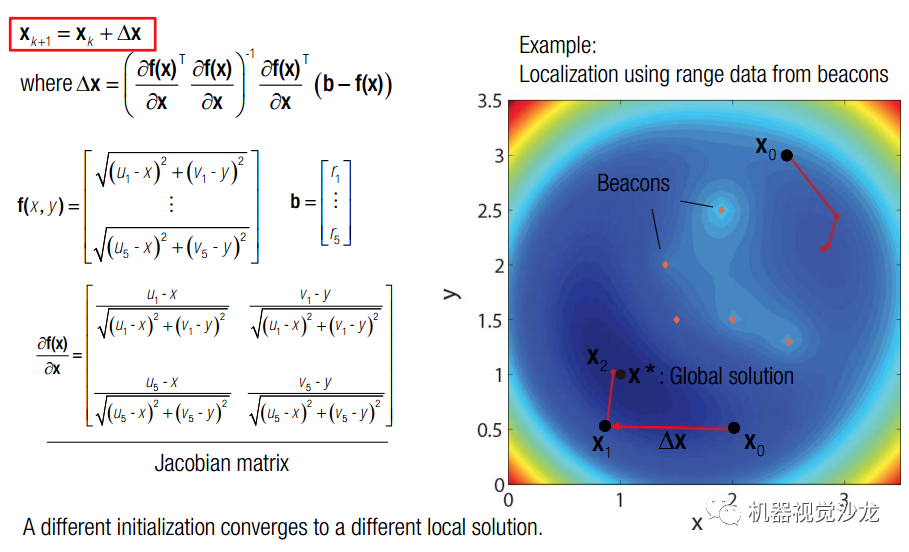
线性最小二乘法已经有了很好的解释。但是生活总是如此不易，能化成上述标准矩阵形式的问题毕竟还是少数，大部分情况下，我们面对的不是min（||Ax - b||），而是 min（||f（x）-b||） ！！！

在三维重建中，如果我们有2个以上视角，那么三条线很可能是不交于一点的。原因是我们选择的旋转矩阵有精度表达问题，位姿估计也存在误差。使用奇异值分解的方法是求得到三条线距离最小的点，还有一种合适的估计，是使得该点在三个相机上的重复投影误差最小。同时，R，T，P（X，Y，Z）进行估计，最终保证Reprojection err 最小的方法————the state of the art BUNDLE ADJUST. 先回到最原始的问题，如何求解非线性最小二乘法。

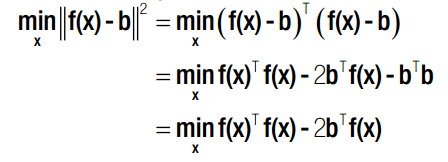
由线性最小二乘法，我们可以得到非线性最小二乘法矩阵表达形式。如果要求得其局部最小值，则对 x 求导后，导数应为 0。

然而，这个东西并不好解，我们考虑使用梯度下降迭代的方式。这里使用的是单纯的梯度。

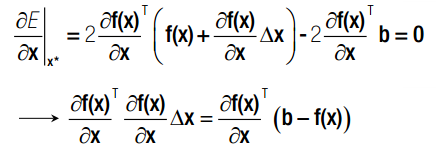
这里有个非常不好理解的地方，其假设detaX非常小，故表示成上述形式，以保证 f（x + deta_X）《f（x） ， 只要依次迭代 x 就能保证每次都向着f（x）减小的方向移动。实际上，这个解应该由hessian矩阵给出。《 span》

以信标定位为例。讲道理，两个信标为圆心画圆应该给出位置的两个解析解。但是如果有很多信标，那么信标就会画出一块区域。..。..。.这是SLAM里的经典问题了，后面会有博客专门讲BUNDLE ADJUST.

（四）极几何是机器人视觉分支——双目视觉中，最为重要的概念。与结构光视觉不同，双目视觉是“主动测量”方法。

1、极几何的研究前提

极几何的研究对象是两幅有重叠区域图像。研究目标是提取相机拍摄位姿之间的关系。一旦得到两次拍摄位姿之间的关系，我们就可以对场景点进行三维重建。

极几何定义的物理量包括4个：1、极点；2、极线；3、基本矩阵；4、本征矩阵；定义如左图。 极几何研究的物理量包括4个：C1坐标，C2坐标，R，T，定义如右图。

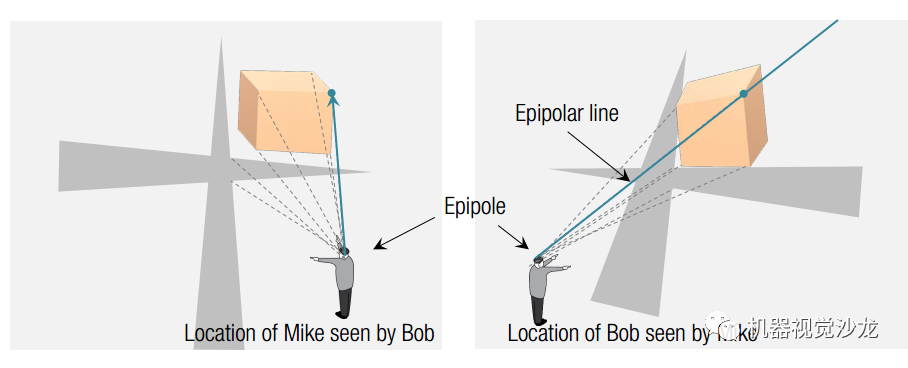
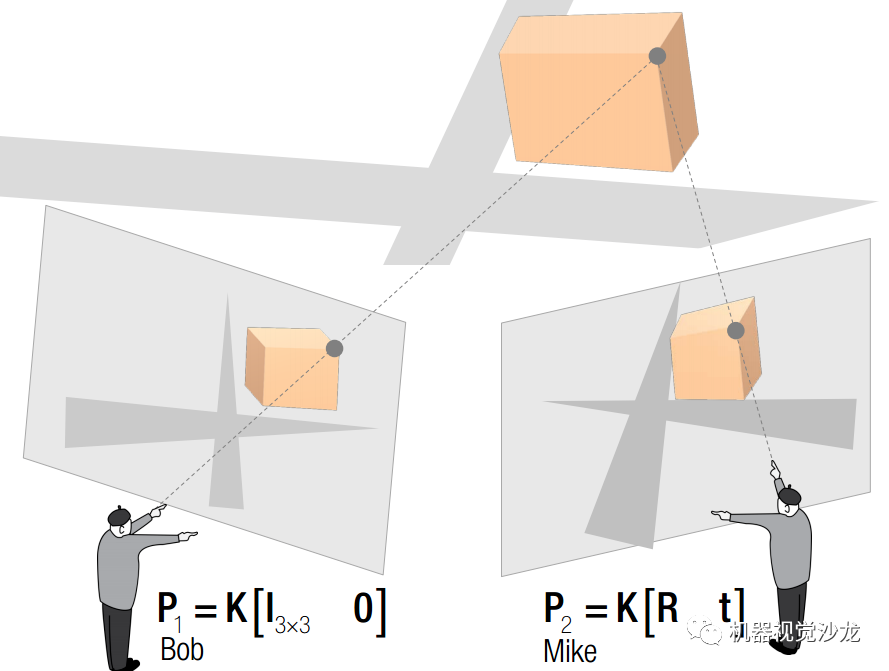
极点的本质是另一台相机光心在本图像上的映射点。极线的本质是另一台相机光线在本图像上的映射线。（极点和极线都是在图像上的）

1.1、本征矩阵

本征矩阵携带了相机相对位置信息。其推导如下： 在相机2的坐标系中，场景点坐标：X2 = RX1+ t 相机1光心坐标：t 极线在空间中的映射 ：X2 - t = RX1 此时，三个向量在同一个平面上，则有：X2 T tx RX1 = 0 其中，tx 代表 t 的叉乘矩阵。tx R 称为本征矩阵E. 两幅图片一旦拍摄完成R与T都是确定的。空间中任何一组对应点都必须满足本征矩阵！

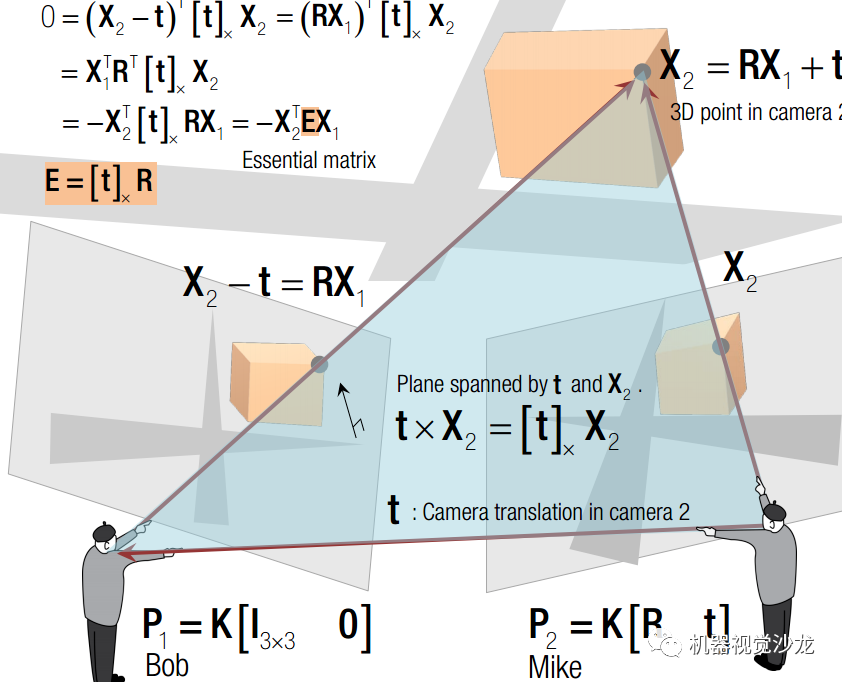
1.2、基本矩阵

空间中的点满足E矩阵，则该点坐标Zoom后，仍然必须满足E矩阵。坐标的Zoom显然和相机内部矩阵有关。 在相机坐标系下： x1 = KX1; x2 = KX2 其中，x1 ，x2 是齐次像素坐标。那么，X1 = K-1x1 ；X2 = K-1x2 带入本征矩阵可得： x2 T K-Ttx RK-1 x1 = 0======》 K-TEK-1 = 0 =========》 x2 T F x1 = 0 F = K-TEK-1 称为基本矩阵。 基本矩阵所接受的是齐次像素坐标。 基本矩阵的秩是2，因为它有0空间。同时，其自由度是8，因为它接受的是齐次坐标。每组图像点可以提供1个方程，所以由8组点就可以线性解出F矩阵。当然，解法是化成Ax = 0，然后使用奇异值分解取v的最后一列。然后2次奇异值分解去掉最小奇异值正则化。

1.3、极点与极线

从基本矩阵可知：x2 T F x1 = 0 显然这里有熟悉的身影，由点线对偶可知，x2 在直线 F x1 上。该直线是极线在图像2上的方程。x1 在直线 x2 T F 。该直线是极线在图像1上的方程。 极点是多条极线的交点（最少两条）

2、由本征矩阵恢复R，T

E = tx R = ［ tx r1 tx r2 tx r3 ］

E的秩为2，因为其有0空间。同时，由于r1 r2 r3 是正交的，所以其叉乘之后必然也是正交的。所以不妨假设其叉乘完之后依然满足旋转矩阵的某些性质。比如：每一列，模相等。 由 tT E = 0 可知，对E奇异值分解之后，t 为最小奇异值所对应的 u（：，end）。 如下：

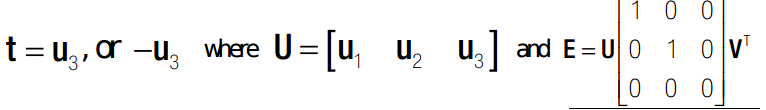
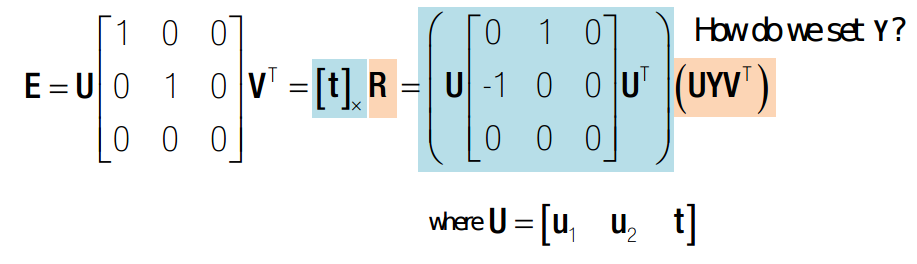
这里假设了 R = UYVT 。因为U，V和R是同族的。所以必然由矩阵Y使得上式成立。V是相互垂直的，R的作用是旋转，U则必然是相互垂直的。所以这里R一定有解，不妨设一个中间变量Y。并很容易解得：

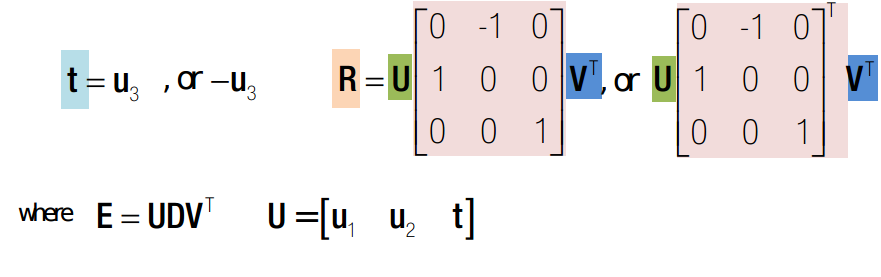
综合来看，由4组可能的解，对应以下四种情况，其中只有第一种是可能的。故det（R） = 1 则猜z中了正确的解，如果det（R） = -1 则解为：t = -t ；R = -R

3、由空间位置关系恢复三维坐标

在已知标定信息，两相机位置关系的情况下，就已知了两个相机的投影矩阵P，对于空间中一点X1，有以下关系： x1= P*X1 ［x1］x P X1 = 0; 显然，我们又有了Ax = 0的神奇形式。奇异值分解搞定之。

4、由RANSAC求 F 矩阵

有了8个对应点，我们就可以求得F矩阵，再加上K，我们就可以对两幅图片进行三维重建。然而想要自动的求取8个对应点还是有一定难度。 SIFT算法提供了一种自动匹配的可能性，然而，匹配结果还有很多误匹配的点。本节的目标是利用RANSAC作为算法基础，基础矩阵作为方法，来对匹配结果进行判断。 首先，由于检测误差等因素，像素点不可能恰好满足基本方程。所以点到极线会有一定的距离。我们采用垂直距离来建模，有以下表达式：

F1表示F的第一列。只要误差小于阈值，都认为该点符合 F 方程。 算法流程如下：1、随机取8个点；2、估计F；3、计算所有点的e，并求#inlier；4、回到1，2，3，如果#inlier变多则更新F_candidate；5、迭代很多次结束，F_candidate 为F的估计值。 RANSAC算法又一次证明了其对噪声超级好的控制能力。

（五）之前说到，机器人视觉的核心是Estimation，求取特征并配准，也是为了Estimation做准备。一旦配准完成，我们就可以从图像中估计机器人的位置，姿态。有了位置，姿态，我们可以把三维重建的东西进行拼接。 从视觉信息估计机器人位姿的问题可以分为三个大类：1、场景点在同一平面上。2、场景点在三维空间中。3、两幅点云的配准。 所有问题有一个大前提就是知道相机内部矩阵K。

1、由单应矩阵进行位姿估计

单应矩阵原指从 R2--R2 的映射关系。

但在估计问题中，如果我们能获得这种映射关系，就可以恢复从世界坐标系 x_w 到相机坐标系 x_c 的变换矩阵。此变换矩阵表达了相机相对于x_w 的位姿。 H = s*K*［r1 r2 t］ —— 假设平面上z坐标为0 s*［r1 r2 t］ = k-1*H —— 利用单应矩阵求取旋转与平移向量 r3 = r1×r2 —— 恢复r3 s 并不重要，只需要对k-1*h1 进行归一化就能求出来。 所以，最重要的就是如何求取两个场景中的单应。在前面我提过从消失点来求取单应关系，但是如果不是从长方形 --- 四边形的映射，我们并没有消失点可以找。 这里要介绍的是一种优雅到爆棚的方法。基于矩阵变换与奇异值分解。JB SHI真不愧大牛。三两句就把这个问题讲的如此简单。

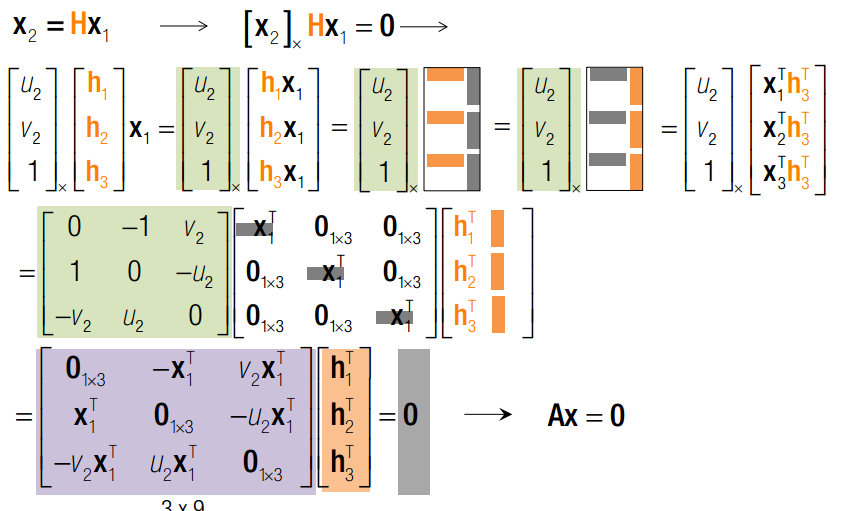
由于H矩阵一共有8个自由度，每一对单应点可以提供两个方程，所以4个单应点就可以唯一确定单应矩阵H。Ax = 0，我们在拟合一章中已经了解过了。x 是最小奇异值对于的V矩阵的列。这里是奇异值分解的第一次出现。 至此，我们恢复了H矩阵。按照正常的思路就可以解除［r1 r2 t］了。但是，我们的H矩阵是用奇异值分解优化出来的，反解的r1 r2 并不一定满足正交条件，也不一定满足等长条件。所以，我们还要拟合一次RT矩阵。 此次的拟合目标是 min（ROS3 - R‘）。 其中R’ = ［k-1H（：，1:2） x ］。 方法依旧是奇异值分解，R = UV‘。 这是奇异值分解的第二次出现。

2、由射影变换进行位姿估计

由单应矩阵进行位姿估计的前提是所有点都在一个平面上。而由射影变换进行位姿估计则舍弃了此前提，故上一节是本节的一个特例。此问题学名为PnP问题：perspective-n-point。

仿造上面的思路，我们依旧可以写成以下形式：

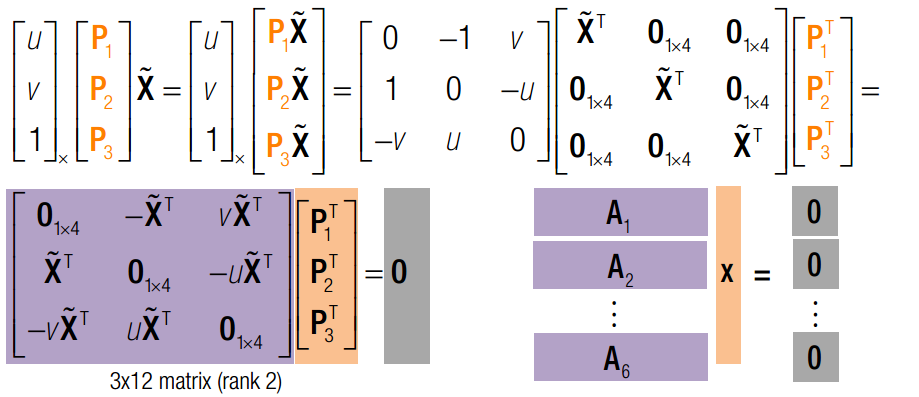
此处射影矩阵一共有12个未知数，9来自旋转矩阵，3来自平移向量。每个点可以提供2个方程。故只要6个场景点，我们就可以用奇异值分解获得P矩阵的值。同样，在获得P矩阵后求T = k-1*P，最后利用奇异值分解修正T. 不过按照常理，此问题只有6个自由度（3平移，3旋转）。我们使用6个点其实是一种dirty method。

3、由两幅点云进行位姿估计

对于现在很火的RGBD相机而言，可能这种情况会比较多。从不同角度获得了同一物体的三维图像，如何求取两个位姿之间的变换关系。这个问题有解析解的前提是点能够一一对应上。如果点不能一一对应，那就是ICP算法问题了。

此问题学名为：Procrustes Problem。来自希腊神话。用中文来比喻的话可以叫穿鞋问题。如何对脚进行旋转平移，最后塞进鞋里。其数学描述如下：通过选择合适的R，T，减小AB之间的差别。

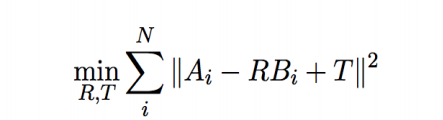
T 其实很好猜，如果两个点团能重合，那么其重心肯定是重合的。所以T代表两个点团重心之间的向量。此问题则有如下变形：

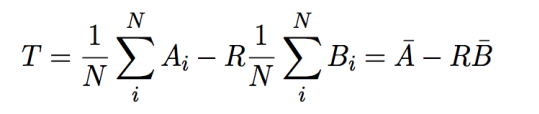
由矩阵分析可知，向量的2范数有以下变形：

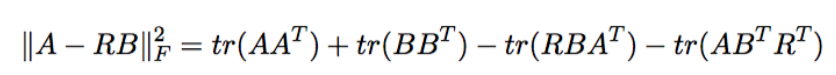
由矩阵分析可知，最后两项实际上是相等的（迹的循环不变性与转置不变性） 那么优化目标又可以转为：

迹是和奇异值相关的量（相似变换迹不变）

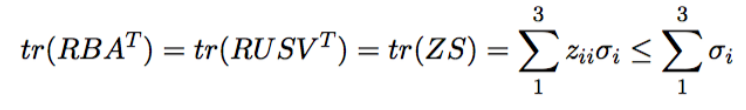
显然，如果Z的迹尽可能大，那么只有一种情况，Z是单位阵，单位阵的迹是旋转矩阵里最大的。所以R的解析解如下：

至此，我们获得了3D--3D位姿估计的解析解！ （六）最后一个话题是Bundle Adjustment. 机器人视觉学中，最顶尖的方法。

1、基于非线性优化的相机位姿估计

之前已经在拟合一篇中，已经补完了非线性最小二乘拟合问题。Bundle Adjustment，中文是光束平差法，就是利用非线性最小二乘法来求取相机位姿，三维点坐标。在仅给定相机内部矩阵的条件下，对四周物体进行高精度重建。Bundle Adjustment的优化目标依旧是最小重复投影误差。

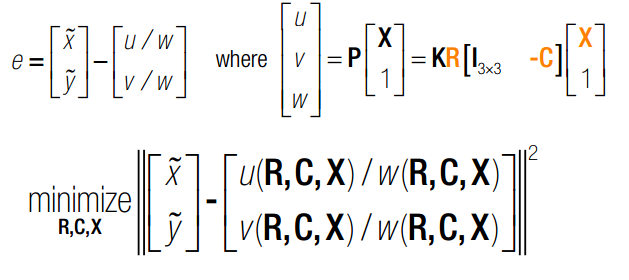
与利用non-linear mean square 解三角同，bundle adjustment 中所有的参数，RCX均为变量。N幅图则有N个位姿，X个点，我们会得到非常大的jacobbian Matrix.本质上，需要使用雅克比矩阵进行梯度下降搜索。详细见之前介绍过的“拟合”篇。

2、雅克比矩阵

雅克比矩阵的行代表信息，列代表约束。 每一行是一个点在该位姿下的误差，每一列代表f对x分量的偏导数。

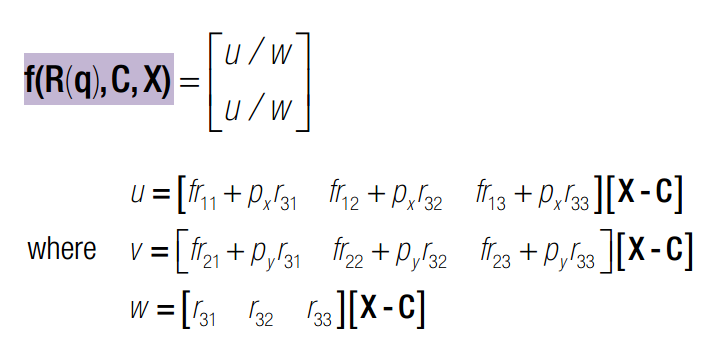
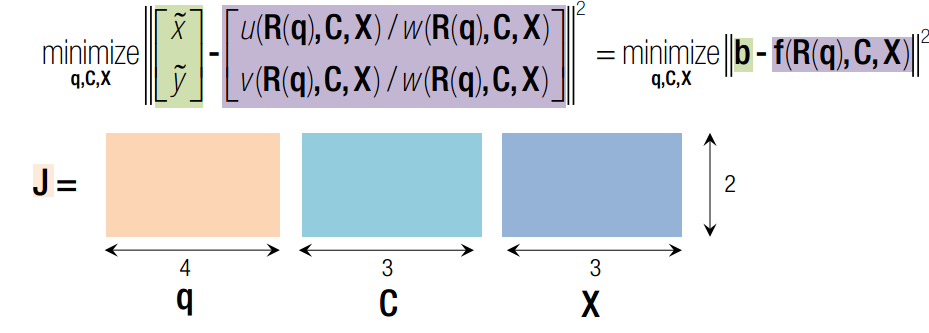
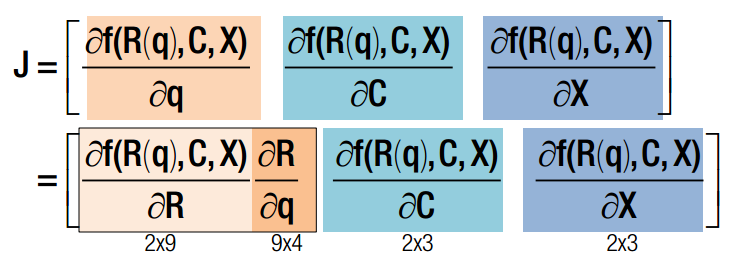
q x c 均为变量，q是旋转四元素，x 是三维点空间坐标，c 是相机光心在世界坐标系下的坐标。J 可以分为三部分，前4列代表对旋转求导，中间三列代表对c求导，最后三列代表对x求导。其中，对旋转求导又可以分解为对旋转矩阵求导X旋转矩阵对四元素q求导。一旦获得J的表达式，我们就可以使用Newton-Gaussian 迭代对x寻优了。求导后的数学表达式如下：

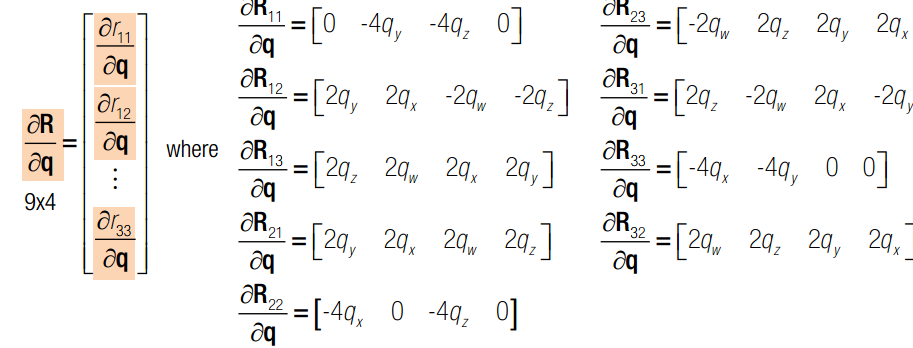
如果有两个相机，则总的雅克比矩阵如下：

通过同时迭代所有的q C X ，最终可以同时得到世界点坐标，相机位姿 ——SLAM！

审核编辑：郭婷