基于六面体单元热应力问题的Matlab有限元编程求解

导读：上一篇《弹性地基梁matlab有限元编程，以双排桩支护结构计算为例》引起了Matlab有限元编程学习者的共鸣。今天我想和大家讨论一下热应力问题（六面体单元）matlab有限元编程问题。

本案例主要介绍热应力问题的matlab有限元编程及原理。热应力也叫温度应力，后文提到的热应变也叫温度应变。这里需要与传热问题的有限元分析进行区分：可以认为传热分析是进行热应力分析的前提条件，通过传热分析来确定温度场，在获得温度场的基础上，计算所产生的热应力。所以本文为阐述热应力问题前提是假定温度场是已知的，我们并不关心温度场是如何得到的，那是热传导要解决的问题，在这个已知的温度场作用下，由于热胀冷缩会产生响应的热应变进而产生热应力，如何求解这个热应力，这就是我们这次课程要解决的问题。

如图1所示，本案例的分析对象为一个两端固定约束的四棱柱受不同方向的热应变作用下产生的应力应变，在用有限元方法求解热应力问题时，温度作用可以等效为一个节点载荷进行求解，因此热应力问题本质上还是一个固体力学问题的有限元求解，而我们刚才提到的传热问题的有限元求解其实是在求解傅里叶传热偏微分方程，其与固体力学偏微分方程是完全不同的两套理论。

因此，本文首先重点讲解的温度作用产生的节点等效温度荷载有限元列式的推导，六面体单元刚度矩阵、雅各比矩阵、应变矩阵有限元列式的推导，温度应力应变的后处理有限元列式，此外还包括上述有限元列式对应的matlab代码实现过程。

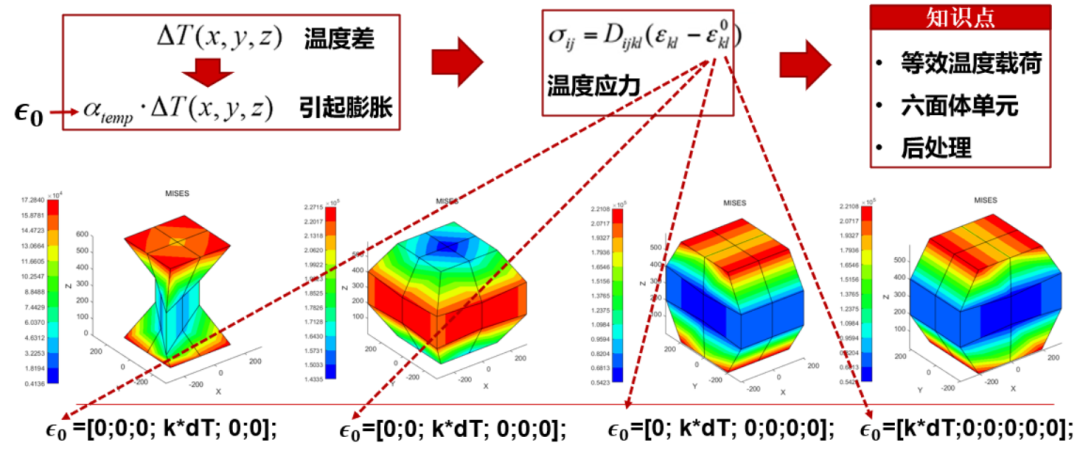
图1 两端固定约束的四棱柱受单位热应变作用下的应力

假定通过传热分析我们可以得到，相对于原来状态温度升高了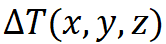，对于各向同性材料，温度升高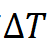会产生一个均匀的应变（通俗地讲，就是热胀冷缩原理，物体会发生膨胀），应变大小与材料的线膨胀系数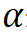有关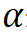，表示材料在单位温度升高所引起的长度的变化值，一般情况下，在一定范围内可以假定线膨胀系数为常数。若物体能够自由变形，则由温度变化引起的应变不会产生应力。温度应变一般被表示为初应变的形式

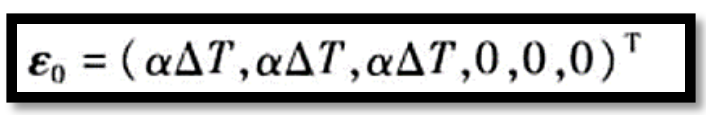    （1）

对应的应力-应变关系为

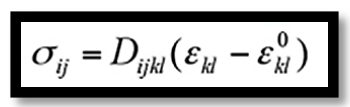        （2）

接下来将公式（2）的应力应变关系代入到有限元分析列式中，利用虚功原理进行推导。其中虚应力和虚应变场函数的有限元列式如下式

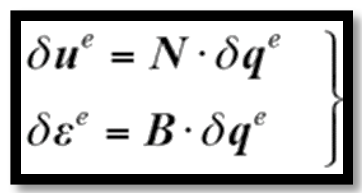           （3）

将公式（2）利用虚功原理，可得到下述虚功方程

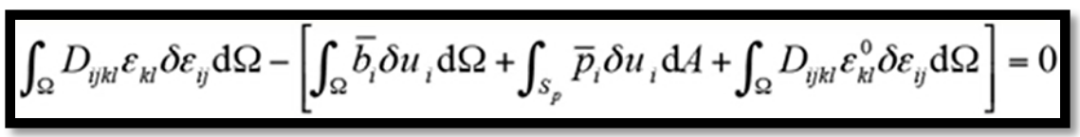      （4）

将公式（3）代入公式（4）所示的虚功方程中，并对其进行简化处理，可以得到

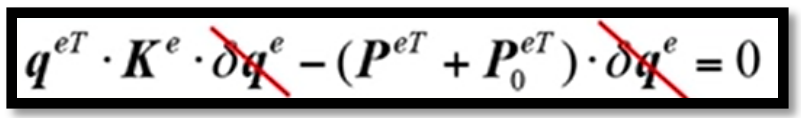    （5）

因为虚位移存在任意性，因此可以除掉公式（5）中的虚位移，进而得到

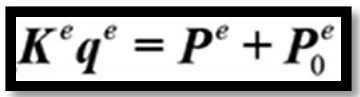     （6）

其中Ke为刚度矩阵，表达式为

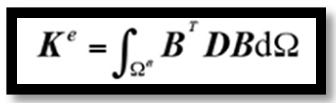       （7）

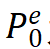为单元节点载荷，表达式为

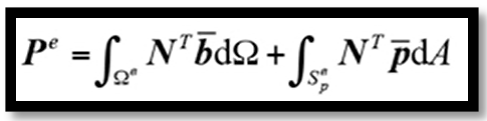      （8）

为等效温度载荷，是由热应力引起的节点处等效温度载荷，表达式为

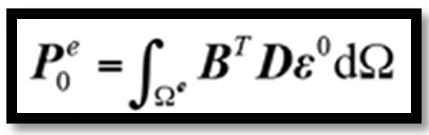        （9）

因此，对于温度应力问题，核心就是求解等效温度载荷。因为公式中包含了B矩阵，即应变矩阵，对于六面体单元应变矩阵的推导过程如下图所示。

图1 应变矩阵与刚度矩阵的推导公式

基于图1所示的应变矩阵的推导过程，公式（9）中等效温度载荷对应的matlab代码如下所示，此外本段代码同样包含了单元刚度矩阵的编程实现，因为等效温度载荷和单元刚度矩阵的求解公式中均有B矩阵和D矩阵参与。

for X=1:2
for Y=1:2
for Z=1:2
GP1=GaussCoordinate(X); GP2=GaussCoordinate(Y); GP3=GaussCoordinate(Z); %高斯点坐标
% 计算形函数对总体坐标的导数（NDerivative）及雅可比矩阵行列式（JacobiDET）
[~,NDerivative, JacobiDET] = ShapeFunction([GP1 GP2 GP3], ElementNodeCoordinate);
Coefficient=GaussWeight(X)*GaussWeight(Y)*GaussWeight(Z)*JacobiDET;
%计算B矩阵  利用形函数对总体坐标的导数（NDerivative）对B进行计算
B=zeros(6,24);
for I=1:8
COL=(I-1)*3+1:(I-1)*3+3;
B(:,COL)=[NDerivative(1,I) 0         0;
0         NDerivative(2,I) 0;
0         0         NDerivative(3,I);
NDerivative(2,I) NDerivative(1,I) 0;
0         NDerivative(3,I) NDerivative(2,I);
NDerivative(3,I) 0         NDerivative(1,I)];
end
Ke=Ke+Coefficient*B'*D*B;  %叠加刚度阵
P_dT=P_dT+Coefficient*B'*D*epsilon0; %等效温度荷载
end
end
end

上述代码中，求解雅各比矩阵行列式和形函数导数的ShapeFunction函数的matlab代码如下所示：

function [N,NDerivative,JacobiDET] = ShapeFunction(GaussPoint,ElementNodeCoordinate)
%等参元坐标  每一列代表一个点的坐标
ParentNodes=[-1 1  1 -1 -1  1  1 -1;
-1 -1  1  1 -1 -1  1  1;
-1 -1 -1 -1  1  1  1  1];
N=zeros(8,1); %初始化形函数矩阵8*1
ParentNDerivative=zeros(3,8);%初始化形函数对局部坐标的导数矩阵3*8
%计算形函数及形函数对局部坐标导数
for I=1:8
XPoint = ParentNodes(1,I);
YPoint = ParentNodes(2,I);
ZPoint = ParentNodes(3,I);
ShapePart = [1+GaussPoint(1)*XPoint 1+GaussPoint(2)*YPoint 1+GaussPoint(3)*ZPoint];  %定义中间变量
N(I) = 0.125*ShapePart(1)*ShapePart(2)*ShapePart(3);
ParentNDerivative(1,I) = 0.125*XPoint*ShapePart(2)*ShapePart(3);
ParentNDerivative(2,I) = 0.125*YPoint*ShapePart(1)*ShapePart(3);
ParentNDerivative(3,I) = 0.125*ZPoint*ShapePart(1)*ShapePart(2);
end
Jacobi = ParentNDerivative*ElementNodeCoordinate;%计算雅可比矩阵
JacobiDET = det(Jacobi);%计算雅可比行列式
JacobiINV=inv(Jacobi);%对雅可比行列式求逆
NDerivative=JacobiINV*ParentNDerivative;%利用雅可比行列式的逆计算形函数对结构坐标的导数3*8
end

单元刚度矩阵和等效温度载荷求得之后，将其装配到整体刚度矩阵和荷载向量中通过高斯消去法实现节点位移的求解，求解之后的节点位移按照下图中的后处理流程和对应的公式，即可求解得到高斯积分点处的应力应变值，需要注意的是如公式（2）所示单元应力的求解公式中包含了温度应变；下一步再通过插值函数矩阵将高斯积分点处的应力应变插值到每个节点再进行磨平处理，即可得到节点的应力应变。具体matlab实现代码如下所示：

InterpolationMatrix=zeros(8,8);%求解节点应力应变的插值矩阵
%循环高斯点
for X=1:2
for Y=1:2
for Z=1:2  
E1=GaussCoordinate(X); E2=GaussCoordinate(Y); E3=GaussCoordinate(Z);
GaussPointNumber = GaussPointNumber + 1;
% 计算局部坐标下的形函数及形函数导数
[N,NDerivative, ~] = ShapeFunction([E1 E2 E3], ElementNodeCoordinate);
ElementNodeDisplacement=U(ElementNodeDOF);
ElementNodeDisplacement=reshape(ElementNodeDisplacement,Dof,8);
% 计算高斯点应变 GausspointStrain3_3 3*3的应变矩阵
GausspointStrain3_3=ElementNodeDisplacement*NDerivative’;%3*8  8*3
%把高斯点应变矩阵改写成6*1
GausspointStrain=[GausspointStrain3_3(1,1) GausspointStrain3_3(2,2) GausspointStrain3_3(3,3)…  
GausspointStrain3_3(1,2)+GausspointStrain3_3(2,1)…
GausspointStrain3_3(2,3)+GausspointStrain3_3(3,2) …
GausspointStrain3_3(1,3)+GausspointStrain3_3(3,1)]';
% 计算高斯点应力
GausspointStress = D*GausspointStrain-D*epsilon0;%总应变-温度应变
GaussStrain(:,GaussPointNumber)=GausspointStrain;
GaussStress(:,GaussPointNumber)=GausspointStress;
InterpolationMatrix(K,:)=N;
K=K+1;
end
end
end
%求得节点应力应变
Temp1=InterpolationMatrix(GaussStrain(1:6,GaussPointNumber-7:GaussPointNumber)');
NodeStrain(1:6,INODE+1:INODE+8)=Temp1';
Temp2=InterpolationMatrix(GaussStress(1:6,GaussPointNumber-7:GaussPointNumber)');
NodeStress(1:6,INODE+1:INODE+8)=Temp2';

上述便是热应力问题的整个求解过程，以一个两端固定约束的四棱柱为例，其在不同单位热应变的作用下的求解结果如下图所示

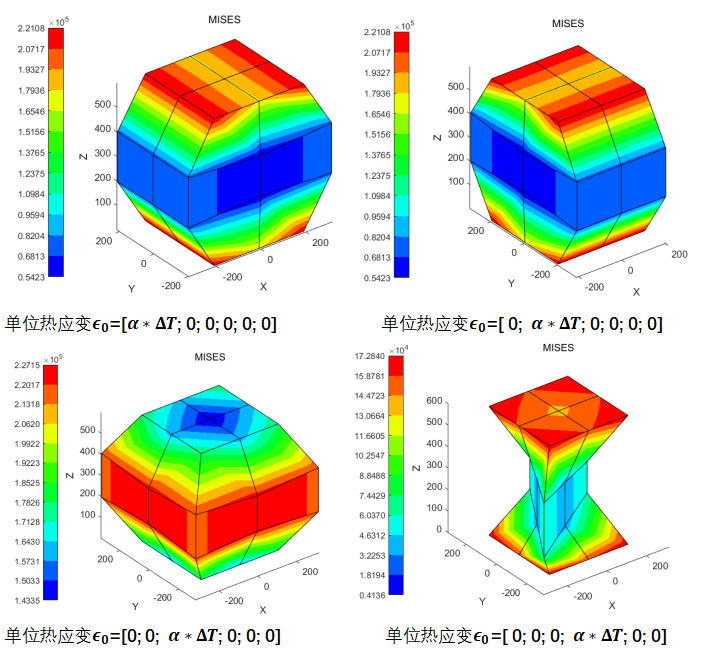
以上就是笔者本期要分享的内容。

审核编辑：汤梓红