信号经过傅立叶变换所得频谱的物理意义讨论

本文讨论了信号经过傅立叶变换所得频谱的物理意义，其中着重于负频率成分。许多信号与系统的教材中，都认为负频率成分没有物理意义。本文以多方面的实例证明了负频率成分不但具有明确的物理意义，而且有重要的工程应用价值。文章还用Matlab程序演示了如何用几何方法求傅立叶反变换，把集总频谱合成为时域信号，从中也可鲜明地看出负频率成分的意义。

1 负频率与复信号

频率的原始定义是每秒出现的次数，可用以衡量机械运动、电信号、乃至任何事件重复出现的频度，这当然不存在有“负”的概念。当用频率描述圆周运动时（即进入了二维信号平面），产生了角频率ω的概念。从机械旋转运动出发，ω=dθdt定义为角速度。对于周期运动，角速度也就是角频率。通常以逆时针为正，因此转动的正频率是逆时针旋转角速度，负频率就是顺时针旋转角速度。正号和负号是非常自然形成的，不存在有无物理意义的问题。

电的单位向量（电压或电流）围绕原点的转动，可以用0 表示，这是在电路中都清楚的。θ的正负所代表的物理意义从来没有什么争议，它的导数ω=dθ/dt的物理意义不言自明。取正取负都不影响定义，为什么取负就会失去物理意义了呢？

在信号与系统课程中为简化问题，便于初学者掌握概念，开宗明义地把研究范围限定于实信号f（t），也就是在电压旋转向量）中，只研究它在实平面或虚平面上的一个投影sin（ωt）或cos（ωt），研究复信号 ejωt的特性与只研究实信号sin（ωt）或cos（ωt）是两个不同的层次。前者（复信号）是反映信号在空间的全面特性，如图1所示。后者（实信号）只研究了信号在一个平面（x-t或y-t组成的平面）上投影的特性。这就必然要丢掉一些重要的信息，以致x=sin（ωt）与sin（−ωt）在z-t平面中的波形没有任何差别，这是人们对负频率的意义产生疑问的直接原因之一。很显然，在x-t 或y-t的平面内，是不可能看出旋转的。既看不到θ ，也看不到ω 。只有在x-y平面上才能看到这两个旋转参数。

注意上述所说的x平面对应实部 ，y平面对应虚部，也就是说此文章是站立在复数表示已经有相应的物理意义的前提下进行的讨论，那么我先给了j一个有效的理论支持，电路理论中 j，-j，-1， 都可以看成是旋转因子。复数 F 乘以j，相当于 F 在复平面中逆时针旋转90度 ；复数 F 乘以 -j，相当于顺时针旋转 90度；F 乘以或除以 -1， 相当于 F 顺时针或逆时针旋转180度

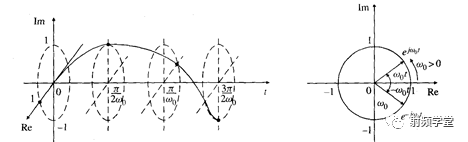
图1 复信号ejωt

2 复信号与实信号的频谱

同样，用 ejωt、sin（ωt）或cos（ωt）作为核来做傅立叶变换所得的结果也是复信号全面，实信号片面。对实信号做傅立叶变换时，如果用指数ejωt为核，将得到双边频谱。以角频率为n的余弦信号为例，它有具有位于±n两处的、幅度各为0.5、相角为零的频率特性。它的几何关系可以用图2表示。两个长度为0.5的向量：分别以士n等速转动，它们的合成向量就是沿实轴方向酌余弦向量 简沿虚轴方向的信号为零。可见必须有负频率的向量存在，才可能构成纯粹的实信号。所以欧拉公式）

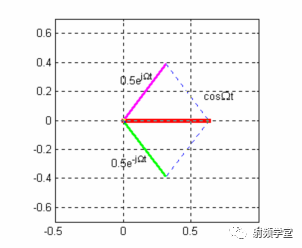
图2 实数信号由正负频率复向量合成

4）多普勒频率

多普勒频率又是一个负频率的实例，如果信号的发射源向我们运动而来，那么多普勒频率就是正频率；如果信号的发射源向我们远离而去，那么多普勒频率就是负频率，在这里正负频率都是有明确物理意义的。多普勒频率虽是一种差频，它表现为合成信号的包络频率，因此仍然符合上述的原理，在实信号域只能求出多普勒频率的大小，但检测不出它的正负。要得到负频率，必须从复信号域考虑。可见，不懂得这一点，就无法找到多普勒测速的原理框图。

归根到底，转角和频率的正负，必须在x-y平面或二维信号中才能观察到。因为观察的方法不对，看不到其意义，从而否认它的存在，这是认识论上的错误，不是科学的方法。这就和“瞎子摸象”的故事所说的那样，摸象腿的人否认象有鼻子，毛病出在他的验证方法。他老想在象腿（实信号域）上找到象鼻子（负频率），当然也永远找不到。正确的方法是必须换一个角度，摸别的部位（复信号域），才能得到全面的知识。

某些学者不承认负频率是由于把“频率是每秒钟循环的次数”的陈旧概念绝对化，其实频率的概念是不断发展充实的。每秒次数的概念只能粗糙地研究信号外部形态，无法涉及信号每周期内部的细微波形特征，而这恰好是傅立叶变换的任务。从它的核已经可以清楚地看到，正是它摒弃（或发展）了原始的频率定义，采用了角频率的概念。单位是弧度/秒，而且具有明确的方向和正负号。其实频率的概念还在继续发展，进入到数字信号处理时又进一步出现了数字频率，它的单位是弧度（去掉了分母上的“秒”），取值范围是［-π，π］。它的物理意义已变为两次采样时刻之间向量转过的角度，在文献［1］中对此有详细的说明。如果停留在“每秒次数”的旧概念上，那“数字信号处理”也就无法发展了。

5．从认识论角度纠正对负频率的错误说法

这个问题是从教学中提出的，作者在旁听“信号与系统”课程时，在老师的幻灯片上看到了“关于双边谱，负频率只有数学意义，没有物理意义”的提法。我们觉得这是个错误，而且恐怕不是个别老师的想法。回来一查，果然如此，很多相当权威的主流教材上都这么写。

其实，“×××只有数学意义，没有物理意义”这样的“命题”谁也没有证明过，也是无法证明的，它最多只能算是猜想。只要有一个反例就可被推翻，本文已经举出了多个反例，说明它是完全错误的。教师绝不该把错误的猜想说成真理，更不能写在书上和幻灯片上去误导学生。数学是更抽象、更深刻地描述物理现象的工具，而物理是实证的科学。限于条件，人们往往暂时还认识不到数学定理的物理意义。数学超前物理是科学史上多次出现的现象，比如虚数、非欧氏几何等。这时应该努力去理解它，认识它，而不是轻易地放弃它、否定它。自己没想通，没找到的事物，不能说它不存在。给学生讲课时，只能说“我们目前还没有想通×××的物理意义”。这才能表明教师在科学上的严肃和谦逊，也有助于培养学生的科学钻研和创新精神。

6．结束语

讨论这个问题，不仅是理论上的探讨，对于提高教学质量是有重大意义的。今天，信息技术如此的发展，很大程度是由于深入大量地开发频谱资源的结果。在同学刚进入这个资源库的时候，我们要引导他们对这个宝藏发生极大的兴趣，非常珍惜这个宝藏，去深钻，去挖掘它的每一点潜力。不能为了省事，为了堵住学生的好奇提问，轻率地、毫无根据地一句话就把频谱的负频率半边扔掉了。在入门的时候，当然不可能把本文说的概念统统灌输给学生，要顺序渐进。但老师首先要有更宽广的知识面和更科学的思维方法，教出的学生的才会具备更多的想象力和创造性。

审核编辑：郭婷