FFT（快速傅里叶变换）波形分析

要计算FFT（快速傅立叶变换），只需听听。人耳自动且不由自主地执行一项计算，这需要多年的数学教育才能完成。耳朵通过将声音（随时间传播和穿过大气的压力波）转换为频谱来制定转换，将声音描述为一系列不同音高的体积。然后，大脑将这些信息转化为感知的声音。

类似的转换可以在相同的声波或几乎任何其他随时间变化的波动信号上使用数学方法完成。傅里叶变换是用于进行此转换的数学工具。简单地说，傅里叶变换将时域中的波形数据转换为频域。傅里叶变换通过将原始基于时间的波形分解为一系列正弦项来实现这一点，每个项都有独特的幅度、频率和相位。实际上，这个过程将时域中难以用数学描述的波形转换为一系列更易于管理的正弦函数，当它们加在一起时，可以精确地再现原始波形。绘制每个正弦项的幅度与其频率的关系图可以创建一个功率谱，这是频域中原始波形的响应。图1说明了这种时域转换概念。

傅里叶变换已成为不同科学领域的强大分析工具。在某些情况下，傅里叶变换可以提供一种求解描述对电、热或光的动态响应的笨拙方程的方法。在其他情况下，它可以识别对波动信号的常规贡献，从而有助于理解天文学，医学和化学中的观测结果。也许是因为它的有用性，傅里叶变换已被改编用于个人计算机。已经开发出算法，将个人计算机及其评估大量数字的能力与傅里叶变换联系起来，为频域中波形数据的表示提供基于个人计算机的解决方案。但是您应该在傅里叶分析软件中寻找什么？是什么让一个软件包在功能、灵活性和准确性方面优于另一个软件包？本应用笔记将介绍并解释此类软件包的一些元素，试图消除围绕这个强大分析工具的神秘面纱。

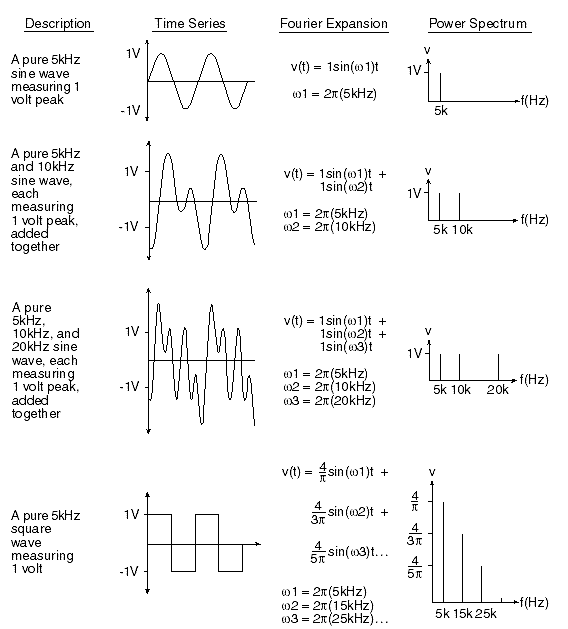
图 1 — 图示傅里叶变换

DATAQ Instruments的WinDaq波形浏览器（WWB）回放软件包含一个傅里叶变换算法，该算法是本应用笔记的模型，包括本文讨论的傅里叶变换的所有元素。本说明中介绍的所有图形和概念也派生自 WWB 傅里叶变换实用程序。

变形三重奏

在计算机出现之前，傅里叶变换的数值计算是一项非常劳动密集型的任务，因为如此大量的算术必须用纸和铅笔进行。随着计算机和程序的开发，这些计算变得更加实用，以实现傅里叶分析的新方法。其中一种方法是由James W. Cooley和John W.Tukey 1于1965年开发的，他们的工作导致了一种称为快速傅里叶变换的程序的开发。快速傅里叶变换 （FFT） 是一种生成傅里叶变换的计算效率高的方法。FFT的主要优点是速度，它通过减少分析波形所需的计算次数来实现速度。与FFT相关的缺点是可以转换的波形数据范围有限，并且需要对波形应用窗口加权函数（待定义）以补偿频谱泄漏（也有待定义）。

FFT的替代方案是离散傅里叶变换（DFT）。DFT 允许您精确定义计算转换的范围，从而消除了窗口的需要。不利的一面是，DFT的计算速度比FFT慢。

从时域到频域的转换是可逆的。一旦功率谱由前面提到的两个变换之一显示，就可以通过计算傅里叶逆变换（IFT）将原始信号重建为时间的函数。这些变换中的每一个都将在以下段落中单独讨论，以填补缺失的背景，并为市场上各种傅里叶分析软件包之间的比较提供标准。

使用 FFT 生成功率谱

FFT只是DFT的更快实现。FFT 算法将 n 点傅里叶变换减少到大约

（不适用） 日志2（n）

复杂的乘法。例如，直接计算，1，024（即210）数据点的DFT将需要

n 2= 1，024 × 1，024 = 220= 1，048，576

乘法。FFT 算法将其减少到大约

（n/2） log2（n） = 512 × 10 = 5，120

乘法，提高 200 倍。

但速度的提高是以牺牲多功能性为代价的。FFT函数自动对要评估的时间序列施加一些限制，以产生有意义、准确的频率响应。由于 FFT 函数根据定义使用以 2 为底的对数，因此它要求要评估的时间序列的范围或长度包含精确等于 2 次方到 n 次方数的数据点总数（例如，512、1024、2048 等）。因此，使用 FFT，您只能评估包含 512 个点、1024 个点或 2048 个点等的固定长度波形。例如，如果时间序列包含 1096 个数据点，则使用 FFT 一次只能评估其中的 1024 个数据点，因为 1024 是小于 1096 的最高 2 次方 n 次方。

由于这种 2 次方到 n 次方的限制，出现了另一个问题。当FFT评估波形时，波形的一部分被包围为512点，或1024点，依此类推。这些边界之一还在波形上建立一个起点或参考点，该起点或参考点在确定的间隔后重复，从而定义波形的一个完整周期或周期。任意数量的波形周期，更重要的是，在这些边界之间可以存在部分波形周期。这就是问题发展的地方。FFT函数还要求要评估的时间序列是相应的周期函数，或者换句话说，时间序列必须包含图2a所示的整数个周期，以产生准确的频率响应。显然，波形包含的点数等于 2 的 n 次方数并以整数个周期结束的可能性充其量是微乎其微的，因此必须采取措施来确保频域中的准确表示。在我们研究确保频域精度的方法之前，让我们仔细看看全部/部分周期数困境。

如果在不包含图2b所示整数周期的波形上执行FFT，会发生什么情况？

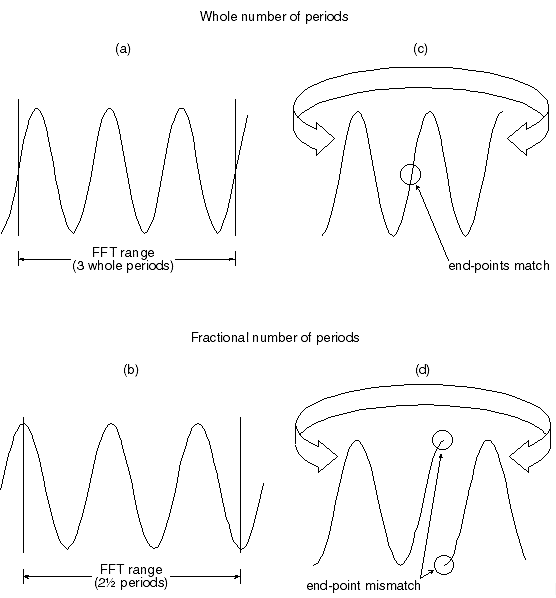
图 2— 波形连续性与不连续性的示例，避免了复杂的数学解释。（a） 显示最佳情况，百万分之一的波形，其中 FFT 的范围正好包含整数个周期，从波形平均值开始。该波形具有终点连续性，如（c）所示，这意味着得到的功率谱将是准确的，不需要应用窗口。更典型的遭遇如（b）所示，其中FFT的范围不包含整数个周期。该波形端点的不连续性（d）意味着产生的功率谱将包含输入中不存在的高频分量，需要应用一个窗口来衰减不连续性并提高精度。

将要评估的波形长度视为已展开的环。如果将未卷绕环的两端重新连接在一起以再次形成一个环，则由整数周期组成的波形将完美地连接在一起，如图2c所示。然而，如图2d所示，由分数点数组成的波形不会完美地连接在一起，两端之间没有间隙或重叠。因此，FFT将使用端点误差评估该波形，并生成包含代表端点失配的虚假频率分量的功率谱。考虑图3所示的光谱。该图显示了振幅和频率相等的两个正弦波的功率谱。然而，正确功率谱的峰值似乎有些“分散”。这种不准确性是对不包含整数周期的波形执行FFT的结果。正确功率谱的扩散或“泄漏”效应是由于波形端点的不连续性人为产生的能量。

幸运的是，有一种解决方案可以最大限度地减少这种泄漏效应误差并确保频域精度。除了DFT（待定义）之外，唯一的解决方案是在执行FFT之前将时间序列乘以窗口加权函数。大多数窗口加权函数（通常称为“窗口”）通过将窗口两端的信号逐渐变细至零来衰减不连续性，如图5d所示。但是，如果您的波形在窗口的末端出现重要信息，它将被锥形破坏。在这种情况下，必须寻求窗口以外的解决方案。通过窗口方法，FFT处理的周期性错误信号将在端点处平滑过渡，从而产生更准确的功率谱表示。存在许多窗口。每个窗口都有不同的特性，使一个窗口在分离频率上彼此靠近的频谱分量，或隔离一个比另一个小得多的频谱分量，或任何任务方面比其他窗口更好。一些流行的窗户（以其发明者的名字命名）是汉明，巴特利特，汉宁和布莱克曼。汉明窗口提供熟悉的钟形加权功能，但不会使窗口边缘的信号归零。汉明窗口产生了非常好的光谱峰值，但只能减少公平的光谱泄漏。Bartlett窗口提供三角形加权功能，使窗口边缘的信号归零。该窗口产生良好、尖锐的光谱峰值，并且还擅长减少光谱泄漏。汉宁窗口提供了一个类似的钟形窗口（如图5d所示，与汉宁窗口的形状非常近似），这也使窗口边缘的信号为零。汉宁窗口产生了良好的光谱峰值清晰度（与巴特利特窗口一样好），但汉宁提供了非常好的光谱泄漏减少（优于巴特利特）。布莱克曼窗口提供类似于汉宁的加权功能，但形状更窄。由于形状较窄，Blackman窗口在减少光谱泄漏方面效果最好，但权衡只是公平的光谱峰值清晰度。如图4所示，窗口函数的选择是一门艺术。这取决于您操纵各种窗口约束之间的权衡的技能，以及您希望从功率谱或其逆中得到什么。显然，提供多个窗口选择的傅里叶分析软件包对于消除FFT固有的频谱泄漏失真是可取的。

简而言之，FFT是一种计算快速的方法，可以根据波形的2到n次方数据点部分生成功率谱。这意味着在功率谱中绘制的点数不一定像最初预期的那么多。FFT还使用一个窗口来最小化由于端点不连续性引起的功率谱失真。然而，这个窗口可能会衰减出现在待评估时间序列边缘的重要信息，并扭曲IFT操作（待定义）的结果，如图5d所示。由于FFT固有的这些限制，您正在考虑的傅里叶分析软件包是否提供FFT以外的解决方案？

另一种解决方案放弃了窗口化，转而允许用户精确定义计算傅里叶变换的范围。这种方法取消了 2 到 n 次方的限制，称为 DFT。

使用DFT生成功率谱

如果需要以比FFT允许的精度更高的精度变换部分波形，或者当需要非窗口变换时，DFT生成就是答案。例如，如果您正在处理瞬态信号，则边缘包含重要信息，这些信息在应用窗口解决方案时会失真，这是不可接受的。在这种情况下，您别无选择，只能使用 DFT。如前所述，DFT允许您调整定义要变换的波形范围的端点，从而消除了对窗口的需要。这种方法允许评估包含任意数量点的波形，这比固定长度、2 次方到 n 次方 FFT 提供了更大的灵活性。然而，为了防止与非窗口FFT相同的泄漏效应，DFT必须在从波形平均电平交叉开始的整数周期内产生。换句话说，必须调整定义将计算DFT的波形范围的终点，以包含或定义整数个周期，最好从波形与其平均值交叉的点开始或附近开始。

DFT比FFT具有更多的多功能性和精度。但是，多功能性和精度是以算法增加的计算时间和增加端点定位所花费的时间为代价的。例如，表1比较了使用DATAQ Instruments的WWB傅里叶变换实用程序在相同波形上生成FFT和DFT所需的计算时间差异。显示的时间以秒为单位，是从没有数学协处理器的基于 386 的 25 兆赫 PC 获得的。由于 WWB 傅里叶变换算法使用整数算术，因此数学协处理器对提高性能的作用很小，因此此软件包不需要。某些软件包要么需要数学协处理器才能运行，要么强烈建议使用数学协处理器以获得最佳性能。请注意，DFT 计算时间仅比 FFT 慢大约四倍。这是因为 WWB 实用程序使用与 FFT 非常相似的计算技术来计算 DFT。结果是计算速度比DFT通常需要的标准n2乘法数快得多。

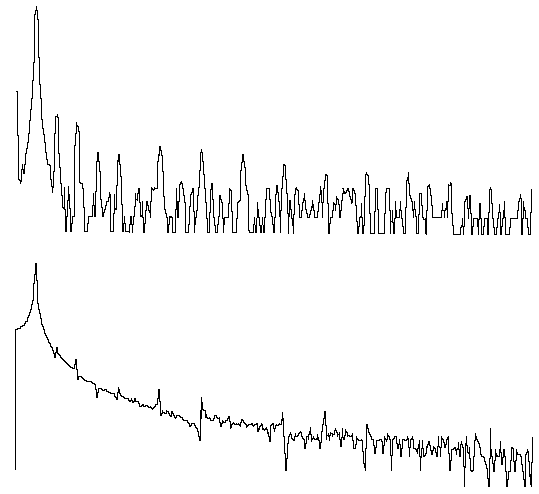
图 3— 正弦波的频谱在单个频率处达到峰值，如上图顶部所示，当对包含整数周期的波形部分执行 FFT 时。如果FFT是在小数个周期上进行的，频谱会给出一个非常不同的图像，如上图底部所示 - 一个宽峰值导致频率确定不良和幅度不准确。这些波形是由廉价的函数发生器产生的，它解释了频谱中存在的噪声。

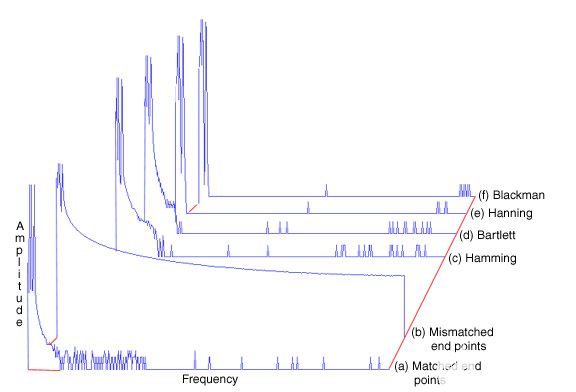
图 4— 两个频率接近但幅度差异很大的正弦波的傅里叶变换很好地说明了窗口选择的重要性。（a） 显示了最佳匹配端点变换，其中明确定义了构成原始波形的两个信号频率，一个在 90 dB 时为 2.2 Hz，另一个在 46 dB 时为 10.9 Hz。更典型的是，（b）仅显示端点不匹配的相同波形的变换。请注意，在这个光谱中甚至看不到第二个峰值。显然需要一个窗口。其余变换说明了各种窗口在抑制频谱泄漏和恢复丢失频率分量方面取得的成功程度。每个窗口都应用于原始波形，结果说明了峰值锐度和旁瓣衰减之间的权衡。（c） 显示汉明窗口。请注意，此窗口永远不会将信号归零。（d） 显示巴特利特窗口，（e） 显示汉宁窗口，（f） 显示布莱克曼窗口。对于这个光谱分离的例子，布莱克曼窗口最擅长将较弱的项作为明确定义的峰。

变换 类型点数

512102420484096819216384

FFT0.30.60.91.42.67.3

DFT1.32.03.35.612.6--

表 1 — 各种点变换的计算时间（以秒为单位）。应该提到的是，DFT是根据一系列数据点计算的，该数据点比所示数字少一个。这样做是为了确保软件将生成DFT。如果它运行在 2 到 n 次方的数据点数（例如，1024 个），则软件足够“智能”，可以识别可以从此数量的数据点生成 FFT 或 DFT。由于DFT意味着更多不必要的计算，因此软件将采用最少计算的路径，从而产生FFT。WinDaq能够使用 FFT 转换最多 16，384 个数据点，使用 DFT 转换 8，191 个数据点。

使用IFT生成时间序列

与其他双边变换（例如矩形到极坐标）一样，傅里叶变换在两个方向上都起作用。如果功率谱（作为频率的函数）要“向后运行”，则原始信号原则上将被重建为时间的函数。这被称为傅里叶逆变换（IFT）。你可能会质疑IFT的目的，如果它所做的只是让你回到你开始的地方。IFT的美妙之处在于它能够在频域中编辑功率谱后让您回到时域。此功能在功率谱滤波应用中非常有用。例如，在许多情况下，需要检查没有任何“噪声”的波形，以扭曲信号的真实性质。这可以通过在执行IFT之前对功率谱应用高通、低通、带通和陷波滤波器功能来完成。高通滤波器将去除功率谱上小于指定点的所有不需要的频率分量，低通滤波器将去除所有大于指定点的不需要的频率分量。带通滤波器是高通和低通滤波器的组合，用于隔离功率谱上的目标窄带。陷波滤波器可去除指定点处不需要的频率分量。图5显示了频域中可能的功率谱编辑类型。滤波操作可以是傅里叶分析软件包中的一项强大功能。

其他傅里叶分析软件问题

任何傅里叶分析应用的需求都可以通过基于图形的软件包得到最好的满足，该软件包允许快速功率谱编辑。除了基本的FFT、DFT和IFT操作外，傅里叶分析软件包的价值还可以通过附带的额外“花里胡哨”进一步增强。

支持波形傅里叶分析的软件包应该能够以工程单位或相对幅度（分贝）显示频率分量的强度，因为转换功率谱幅度单位可能是一项耗时的任务。

另一个问题是功率谱分辨率。除了速度之外，分辨率是 512 点变换和 16，384 点变换之间的唯一区别。功率谱的范围始终从直流电平 （0 Hz） 到被变换波形采样率的一半，因此变换中的点数定义了功率谱分辨率（512 点傅里叶变换的功率谱中有 256 个点，1024 点的傅里叶变换的功率谱中有 512 个点， 等等）。例如，如果要在复杂波形的功率谱中看到单独的 20 和 21 Hz 频率分量，则 512 点傅里叶变换可能无法清楚地显示这些单独的分量，因为它的整个功率谱仅分为 256 个等间距点，并且所需频率非常接近。但是，如果变换包含更多点，它将能够将更多点用于定义紧密间隔的频率分量。变换中的点数越多，频率分辨率越好。

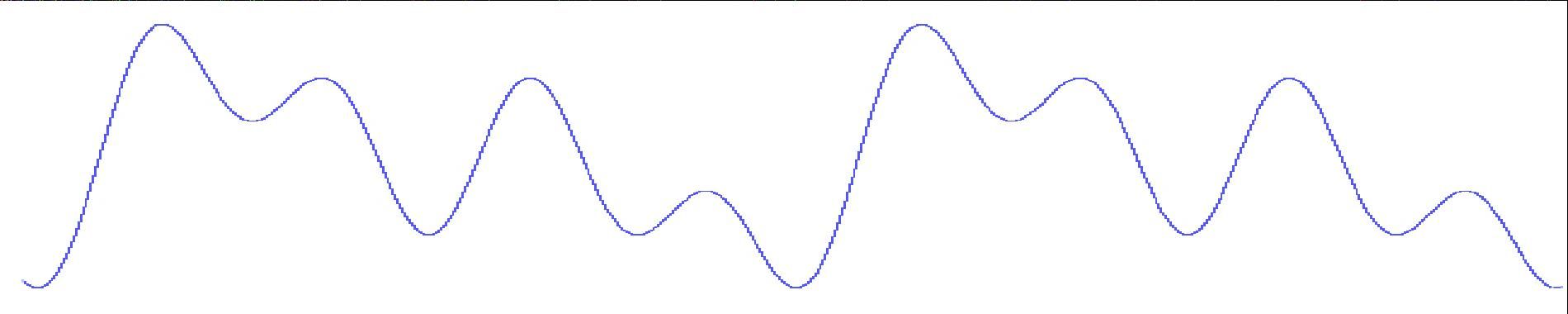
（a） 原始波形

（b） （a）的功率谱

（c） 滤波功率谱

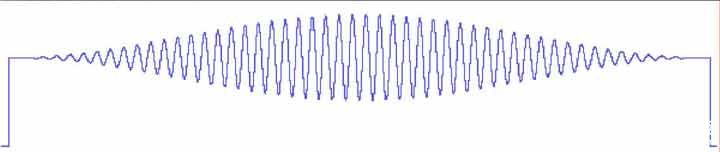
（d） 旅游学院成绩

编辑在频域中进行。（a）所示的波形是包含不良的60 Hz噪声的20 Hz信号。使用512点FFT生成（b）所示的功率谱。在频域中，所有大于40 Hz转折频率的不良频率分量（包括60 Hz噪声）都被编辑掉，或者通过应用低通滤波器（c）将其降低到零。然后从该滤波功率谱生成IFT，产生（d）所示的纯20 Hz波形。注意波形的钟形外观。这是由于汉宁窗口的应用，这是FFT固有的光谱泄漏困境的解决方案。另请注意汉宁窗口如何将窗口边缘的信号衰减到零。如果应用了DFT，这种衰减将被消除，20 Hz信号将从头到尾以全振幅显示。

一个相关的问题是功率谱放大。所考虑的软件应该能够在一个屏幕宽度上显示整个功率谱，而不管变换中的点数如何。这对于发现频谱的整体趋势很有用。通过放大倍率，该软件还应该允许您选择功率谱图的一部分，并使用多个放大倍率因子更仔细地检查它。1024 × 768 的视频标准提供 1024 个水平分辨率的图像元素（像素）。如果执行 512 点傅里叶变换，则变换生成的 256 个点非常适合 1024 像素宽的屏幕。1024 点转换也是如此，其中 1024 像素宽的屏幕足以包含转换生成的 512 点。执行大于 2048 个点的变换时会出现此问题。假设执行了 8192 点傅里叶变换。变换生成的 4096 个点比屏幕的 1024 像素宽度宽得多。为了在一个屏幕宽度上获得整个功率谱，必须应用压缩系数（在本例中为4倍）。然后必须应用放大倍率以检查8192点变换全分辨率下的光谱。此外，当应用禁止在单个屏幕宽度上显示整个功率谱的放大系数时，软件应允许您一次平移一个屏幕宽度的整个绘图。

另一个需要考虑的功能是出口设施。是否可以使用您正在考虑的软件将定义 FFT 图的坐标导出到 ASCII 文件？此功能允许您复制频谱以用于其他程序。

您正在考虑的软件是否允许您在同一波形上快速查看每个窗口的结果？在试验不同类型的窗口以及每个窗口提供的结果时，这可能是一个方便且节省时间的功能。

最后，软件包应该能够进行功率谱平滑。这最好由移动平均实用程序实现。移动平均线是通过从频谱中获取两个或多个数据点，将它们相加，将它们的总和除以添加的数据点总数，将第一个数据点替换为刚刚计算的平均值，然后用第二个、第三个数据点重复这些步骤来实现的，依此类推，直到到达数据末尾。这种简单的平均技术用于衰减功率谱图中经常遇到的随机、小幅度频率尖峰。

审核编辑：郭婷