高级CODAS算法中的多功能移动平均可过滤波形噪声,提取平均值并消除基线漂移。
移动平均线是一种简单的数学技术,主要用于消除像差并揭示数据点集合中的真实趋势。您可能通过平均新生物理实验中的噪声数据或跟踪投资价值来熟悉它。您可能不知道,移动平均线也是有限脉冲响应滤波器的原型,有限脉冲响应滤波器是基于计算机的仪器中最常用的滤波器类型。如果给定波形杂乱无章,需要从周期信号中提取平均值,或者需要从更高频率的信号中消除缓慢漂移的基线,则可以应用移动平均滤波器来实现所需的结果。高级CODAS的移动平均算法提供了这种波形滤波性能。高级CODAS是一个分析软件包,可对第一代WinDaq或第二代WinDaq数据采集包创建的现有波形数据文件进行操作。除了移动平均算法外,高级CODAS还包括报告生成器实用程序和用于波形积分,微分,峰谷捕获,整流和算术运算的软件例程。
移动平均滤波理论
DATAQ 仪器的移动平均算法在波形滤波应用中具有很大的灵活性。它可以用作低通滤波器,以衰减许多类型波形中固有的噪声,或用作高通滤波器以消除较高频率信号的漂移基线。算法用于确定过滤量的过程涉及使用平滑因子。此平滑因子由您通过软件控制,可以增加或减少,以指定移动平均线将跨越的实际波形数据点或样本的数量。任何周期波形都可以被认为是一个长字符串或数据点的集合。该算法通过从采集的波形中获取两个或多个数据点,将它们相加,将它们的总和除以添加的数据点总数,将波形的第一个数据点替换为刚刚计算的平均值,然后用第二个、第三个数据点重复这些步骤,依此类推,直到到达数据末尾,从而完成移动平均线。结果是由平均数据组成的第二个或生成的波形,并且具有与原始波形相同的点数。
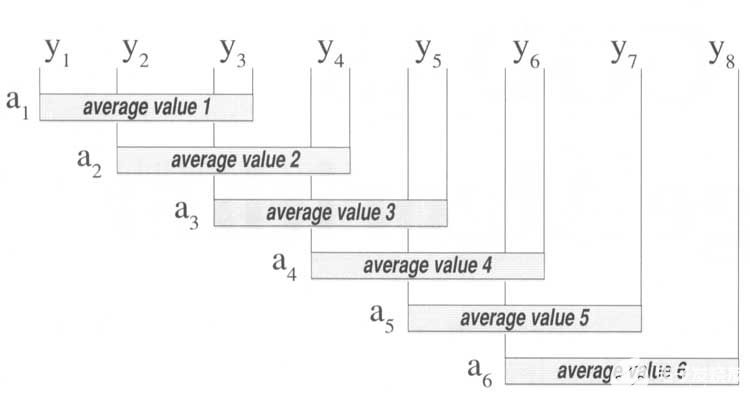
图 1— 任何周期波形都可以被视为长字符串或数据点集合。在上图中,连续的波形数据点用“y”表示,以说明如何计算移动平均线。在这种情况下,应用了3的平滑因子,这意味着将原始波形中的三个连续数据点相加,它们的总和除以3,然后将该商绘制为生成波形的第一个数据点。该过程对原始波形的第二个、第三个等数据点重复,直到到达数据的末尾。一种特殊的“羽化”技术对原始波形的开始和结束数据点进行平均,以确保生成的波形包含与原始波形相同数量的数据点。
图1说明了如何将移动平均算法应用于波形数据点(由y表示)。该图的平滑因子为 3,这意味着将在 3 个连续的波形数据值上计算平均值(用a 表示)。请注意移动平均线计算中存在的重叠。正是这种重叠技术,以及特殊的起点和终点处理,在平均波形中生成与原始波形相同数量的数据点。
该算法计算移动平均线的方式值得仔细研究,并可以通过示例进行说明。假设我们已经节食两周,我们想计算过去 7 天的平均体重。我们将第 7 天的体重与第 8、9、10、11、12 和 13 天的体重相加;然后乘以 1/7。为了使该过程正式化,这可以表示为:
a(7) = 1/7(y(7) + y(8) + y(9) + 。.. + y(13))
这个等式可以进一步推广。波形的移动平均值可以通过以下方式计算:
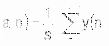
其中:
a = 平均值
n = 数据点位置
s = 平滑因子
y = 实际数据点值
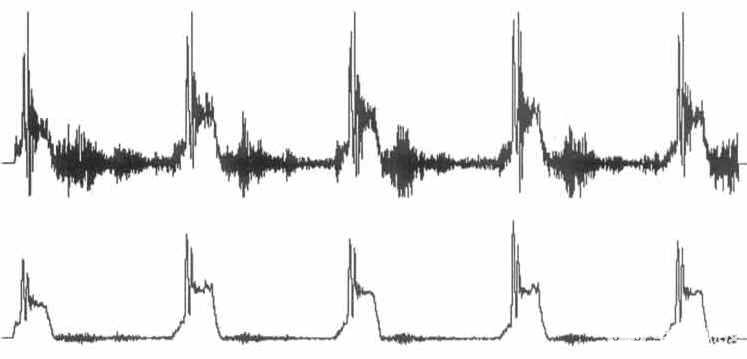
图 2* — 称重传感器输出波形在顶部通道中显示为原始且未经滤波,在底部通道中显示为 11 点移动平均波形。原始波形上出现的噪声是由于印刷机在包装操作过程中产生的强烈振动造成的。
该算法灵活性的关键在于其广泛的可选平滑因子(从 2 - 1,000)。平滑因子确定将平均实际数据点或样本的数量。指定任何正平滑因子可模拟低通滤波器,而指定负平滑因子可模拟高通滤波器。给定平滑因子的绝对值,较高的值对生成的波形应用更大的平滑约束,相反,较低的值应用较少的平滑。通过应用适当的平滑因子,该算法还可用于提取给定周期波形的平均值。较高的正平滑因子通常用于生成平均波形值。
应用移动平均线算法
移动平均算法的一个显着特点是,如果需要,它可以多次应用于同一波形以获得所需的滤波结果。波形滤波是一项非常主观的工作。对一个用户来说可能是正确滤波的波形,对另一个用户来说可能是不可接受的噪声。只有您才能判断选择的平均点数是过高、过低还是恰到好处。该算法的灵活性允许您调整平滑因子,并在初始尝试未获得令人满意的结果时再次通过算法。
移动平均算法的应用和功能可以通过以下示例得到最好的说明。
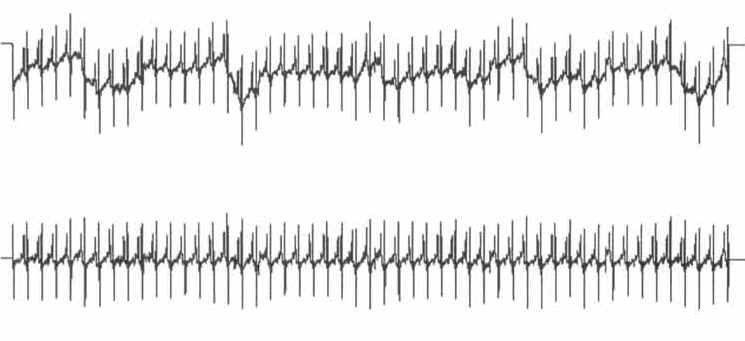
图 3* — ECG 波形在顶部通道中显示为原始且未经滤波,在底部通道中显示为 97 点移动平均波形。请注意,底部通道中没有基线漂移。出于演示目的,两种波形都以压缩状态显示。
降噪应用
在给定波形充满噪声的情况下,可以应用移动平均滤波器来抑制噪声并产生更清晰的波形图像。例如,高级CODAS客户在包装操作中使用压力机和称重传感器。他们的产品将被压缩到预定水平(由称重传感器监控),以减小容纳产品所需的包装尺寸。出于质量控制原因,他们决定使用仪器监控压力机操作。当他们开始查看实时称重传感器输出时,出现了一个意想不到的问题。由于压力机在运行时振动很大,称重传感器的输出波形很难辨别,因为它包含大量噪声,这是由于振动引起的,如图2的顶部通道所示。通过生成一个11点移动平均通道来消除这种噪声,如图2的底部通道所示。结果是称重传感器的输出更加清晰。
消除基线漂移的应用
如果需要从较高频率信号中移除缓慢漂移的基线,则可以应用移动平均滤波器来消除漂移基线。例如,ECG波形通常表现出一定程度的基线漂移,如图3的顶部通道所示。这种基线漂移可以在不改变或干扰波形特性的情况下消除,如图3底部通道所示。这是通过在移动平均线计算期间应用适当的负值平滑因子来实现的。适当的平滑因子通过将一个波形周期(以秒为单位)除以通道的采样间隔来确定。通道的采样间隔只是通道采样率的倒数,可以方便地显示在移动平均实用程序菜单上。通过将光标定位在波形上方便的点,设置时间标记,然后将光标从显示的时间标记上移动一个完整的周期,可以从显示屏轻松确定波形周期。光标和时间标记之间的时间差是一个波形周期,以秒为单位显示在屏幕底部。在我们的ECG示例中,波形具有0.004秒的通道采样间隔(从移动平均实用程序菜单获得),并且测量一个波形周期跨越0.388秒。将波形周期除以通道的采样间隔得到97的平滑因子。由于我们有兴趣消除基线漂移,因此我们对移动平均算法应用了负平滑因子 (-97)。这实际上从原始波形信号中减去了移动平均结果,从而消除了基线漂移,而不会干扰波形信息。
其他波形移动平均线问题
无论何种应用,应用移动平均滤波器的普遍原因是“平滑”高差和低差,并揭示更具代表性的中间波形值。执行此操作时,软件不应在生成移动平均波形的过程中损害原始波形的其他功能。例如,软件应自动调整与原始数据文件相关的校准信息,以便移动平均波形在生成时采用适当的工程单位。
审核编辑:郭婷
-
滤波器
+关注
关注
161文章
7945浏览量
179820 -
计算机
+关注
关注
19文章
7582浏览量
89326 -
数据采集
+关注
关注
39文章
6580浏览量
114718
发布评论请先 登录
相关推荐
深入了解U8g2与LVGL图形库
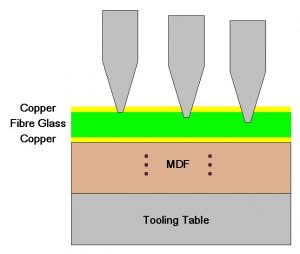
深入了解 PCB 制造技术:铣削
深入了解涡街流量计 原理及内部构造
如何为不同的电机选择合适的驱动芯片?纳芯微带你深入了解!

aes算法在移动应用中的应用场景
深入了解光伏逆变器测试系统

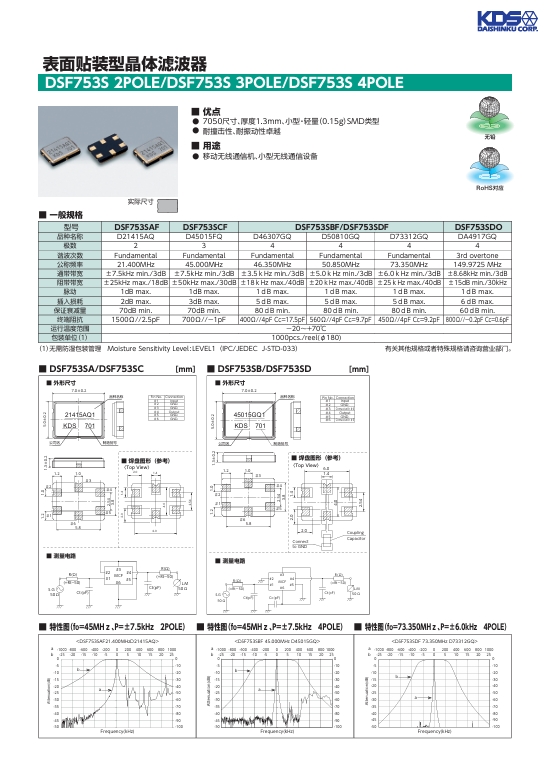
深入了解表面贴装型晶体滤波器:DSF753S 2POLE、DSF753S 3POLE 和 DSF753S 4POLE
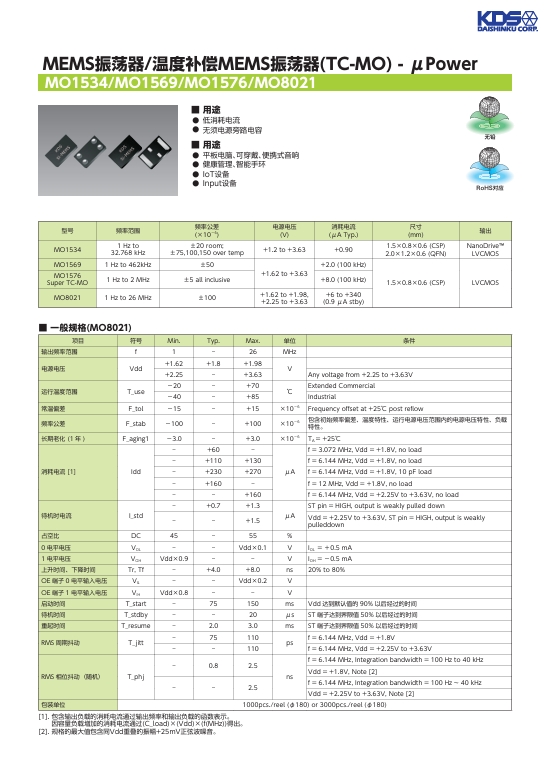
深入了解 MEMS 振荡器 温度补偿 MEMS 振荡器 TC-MO
小熊派官网正式上线 可深入了解小熊派的各款开发套件
深入了解IEEE协会:设备MAC地址申请指南

深入了解北美运营商认证:PTCRB认证指南






 深入了解高级CODAS移动平均算法
深入了解高级CODAS移动平均算法










评论