闭环控制系统是现代自动控制系统的一种典型结构,对于控制专业的工程师,需要选择合适的闭环控制器构型,找出最佳的控制参数,保证被控对象(物理系统)实现预期的行为。在所有开发阶段,MATLAB 和 Simulink 都为控制系统工程师量身定做了一系列的工具,这其中自然也包括了设计和调节反馈控制器。在这个阶段,工程师期望工具能够帮助分析闭环控制的关键性能参数,如超调量、上升时间和稳定裕度,配平和线性化非线性模型,以及未知因素对于模型性能和稳定性的影响等等。
想要实现上述这些功能,并且得到相对“可信”的结果,就必须要有一个能够反映真实物理系统行为的被控对象模型。在传统控制方法,比如PID等控制器构型下,工程师需要基于线性系统理论分析闭环控制的性能,那我们也就不可避免地需要一个线性的被控对象模型。
然而“理想”很丰满,“现实”往往确很骨感。在实际工程领域中,我们常见的被控物理系统(比如飞机、汽车、电机、液压伺服机构),大多都是动态行为十分复杂的非线性系统。诚然我们可以通过线性化的手段,得到这些系统在稳态工况附近的线性模型,从而实现闭环控制参数的调节。但当我们把控制器的作用域放大到整个系统全工况范围内的时候,却发现它的性能往往不太尽如人意,特别是当系统中存在未知干扰的时候。
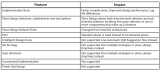
这是因为,当我们建立实际物理系统模型时,我们都是用一个或者几个“确定”的数学表达来反映它的动态行为,这代表无论执行多少次仿真,我们都会针对同样的“输入”得到一致和确定的“结果”。但在真实物理世界中,大部分系统,特别是复杂的非线性系统,都存在一定的不确定性,这样的不确定性普遍存在,其原因大体上可以总结为如下几条:
建立数学模型时的简化,比如降阶;
存在未知的系统参数;
传感器测量噪声;
外部扰动等。
因此,控制系统的设计与实现必须考虑这样的一个问题,即被控对象存在不确定性的情况下,反馈控制器是否仍然能够使闭环控制稳定并能基本满足所期望的性能指标。随着对不确定问题越来越深刻的认识和研究,就导致了专门分析和处理具有不确定系统的控制理论,其中衍生出了两类最具有代表性的理论:鲁棒控制和自适应控制。这两种控制方式都是基于经典线性控制理论的扩展,加入非线性因素以补偿系统在阶次、参数或者信号方面的非预知变化对于控制算法的影响,以达到更好的闭环控制性能。
在后续篇幅中,我们将重点讨论 Simulink Control Design 对于自适应控制理论的支持,特别是在最新发布的 2022b 中,新增加的自抗扰控制器(Active Disturbance Rejection Control,ADRC)的相关内容。
01.自适应控制与 SimulinkControlDesign概述
所谓“自适应”,一般是指系统能够按照环境的变化调整其自身,使得其行为在新的或者已经改变了的环境下达到最好,或者至少满足预先要求的特性和功能,这种对环境变化具有适应能力的控制系统称为自适应控制系统。自适应控制系统可以在没有人的干预下,随着运行环境改变而自动调节自身控制参数,以达到最优的控制。换句话说,自适应控制可以看作是一个能根据环境变化智能调节自身特性的反馈控制系统,以使系统能按照预先设定的标准,工作在最优状态。自适应控制器内部都存在着某种学习机制,从而根据系统的运行状态来自动更新控制参数,适用于被控对象在运行过程中动态特性变化大且带有不确定性的情况。

图 1-自适应控制原理示意
在 MATLAB/Simulink 中,Simulink Control Design 是为控制工程师在 Simulink 环境下进行闭环控制器设计所量身打造的工具。用户可以基于在 Simulink 下建立的被控对象模型,开展闭环控制器的设计,或者基于 Simulink Control Design 提供的丰富资源与案例库,快速搭建闭环控制算法原型,并通过自动代码生成直接部署到硬件进行调整与测试,实现快速原型迭代。在最近的几个 MATLAB 版本中,Simulink Control Design 进行了大幅的更新。在控制设计方面,基于用户对于更先进、更智能的控制算法的应用需求,在最近的几个版本中我们也着力改善了对自适应控制算法的支持,推出了封装好的、直接可用的两个自适应模块:极值搜索控制(Extremum Seeking Control)模块和模型参考自适应控制(Model Reference Adaptive Control)模块,有关于这方面的介绍,可以参阅作者之前发布在公众号上的文章。
02.ADRC模块介绍
与 MRAC 需要参考模型不同,自抗扰控制器(ADRC)是一种不需要模型的自适应控制技术,用于处理被控对象含有未知动态特性或者内外部干扰时的闭环控制问题。ADRC 仅需要被控对象模型动态的近似估计,便可以设计无超调量的干扰抑制控制器。在新版本的 Simulink Control Design 中,提供了封装好的 ADRC 模块,帮助用户在模型中快速搭建此控制算法。该模块目前可以用一阶或者二阶模型近似作为已知的被控对象动态,并通过一个扩展的状态来反映被控对象的不确定性,包括未知的动态特性和干扰。一般情况下,我们可以通过物理系统在工况范围内的开环阶跃响应特性,来确定到底是用一阶模型还是二阶模型来近似已知的被控对象动态。
对于一阶动态近似,
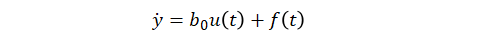
控制器具有如下结构:
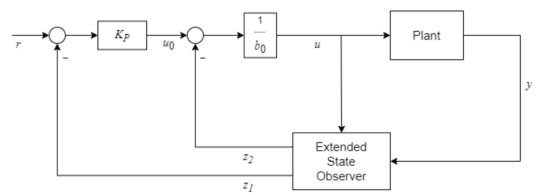
图 2-一阶动态自抗扰控制器结构
此时,控制器为基于估计状态的状态反馈控制器,当估计值与实际值相等时,系统为极点等于 -Kp的闭环一阶系统。
对于二阶动态近似,
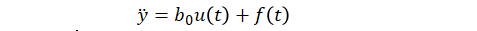
控制器具有如下结构:
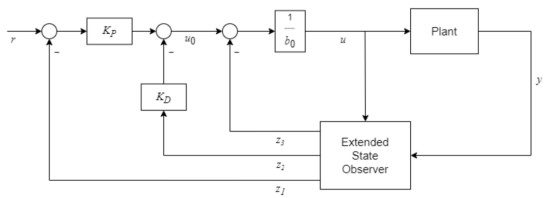
图 3-二阶动态自抗扰控制器结构
此时,控制器为基于估计状态的状态反馈控制器,当估计值与实际值相等时,系统为二阶闭环系统。
上述公式中,y(t)、u(t)、b0和 f(t) 分别代表被控对象的输出、输入、近似增益和未知动态或扰动。模块还使用了扩张状态观测器(Extended State Observer,ESO)来估计 f(t),通过减少估计到的扰动对于模型已知的动态近似的影响,来实现抗扰控制。
从图2和3中可以看到,ADRC 本质上其实还是一个 PID 构型的闭环控制器,但与传统的 PID 控制器相比,由于加入了对于系统大动态变化和未知扰动的观测和抑制,在更加广泛的工况范围内,工程师在参数调节方面所需要的工作量会大幅降低(对比“增益调度”控制方式),有助于保证在非设计工作点下的闭环控制性能。
03.ADRC应用示例
如果只看上述的理论,显得过于枯燥和晦涩的话,在新版本的 MATLAB 中,我们也提供了实际的应用示例,以展示模块的使用方法和效果。对于上述一阶和二阶模型,MATLAB 分别给出了对应的示例,下面对实际工程中常用的二阶系统示例做详细介绍。对于一阶系统示例,可以参阅如下的帮助文档链接。
对于传统的 PID 控制,我们可以通过频率响应估计的方法,得到被控对象电路的线性模型,然后利用 PID Tuner,实现 PID 控制参数的调节,具体方法可以参阅软件帮助文档中的对应示例,在此不再赘述。
针对系统的不确定性或者扰动,我们在模型中添加了如下两个扰动,以查看控制器对于干扰的抑制能力:
T=0.075s时的线路干扰,即输入电压从5V变化为10V;
T=0.09s时的负载干扰,即负载电阻从3欧姆变换为6欧姆。
ADRC 在 MATLAB/Simulink 中为封装好的“即插即用”模块,用户可以通过对话框对其参数进行修改,这包括:
模型阶次;
模型响应近似增益(Critical Gain);
控制器与观测器带宽;
控制器时域类型,这里可以选择连续时间或者离散时间,如果要最终部署在嵌入式设备上,应选择离散时间,并根据前面的控制器和观测器带宽,确定合适的采样周期。
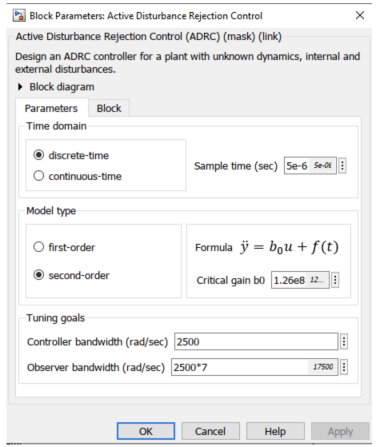
图 5-ADRC模块参数对话框
对于模型的阶次和近似增益,我们可以利用 Simscape Electrical 建立的被控对象模型,进行开环仿真来确定,在输入端,可以给定 Duty Cycle 为 0.5 的 PWM 驱动输入,并截取在输入给定后 0.0005 秒内的电压输出响应。
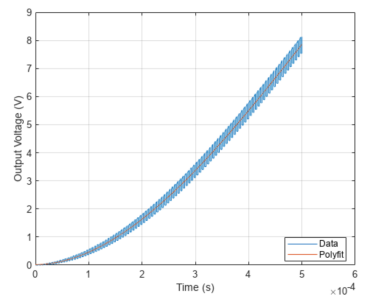
图 6-ADRC被控对象的开环阶跃响应曲线与二阶曲线拟合结果
利用曲线拟合工具,我们可以得到开环系统的被控对象动态特性近似于二阶系统,即
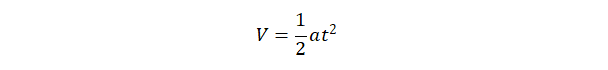
并且得到曲线中的参数,从而得到近似增益估计 b0。
对于控制器带宽,一般取决于对控制性能的要求,而观测器的带宽要高于控制带宽才能满足控制算法部分对于观测器结果的使用要求,一般情况,观测器带宽是控制带宽的 5-10 倍,在本例中选择了 7 倍。
仿真结果可以非常明显地表明在输入电压和负载出现扰动的情况下,ADRC 与传统 PID 相比,具有更好的抗干扰性能,闭环控制的调节时间和超调量指标都明显更优。
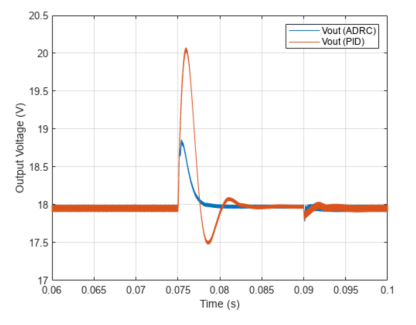
图 7-ADRC与传统 PID控制性能对比
写在最后
随着系统功能的日益复杂,以及硬件平台处理能力的快速提升,以自适应控制为代表的先进控制理论与算法肯定会越来越多地被投入到工程应用当中。而随着大家对物理系统特性本身和控制理论更加深入的研究,像鲁棒控制、模型预测控制、模糊逻辑控制,甚至是强化学习,都将会在未来成为控制工程师口袋中的武器。MathWorks 也会持续在这些方面加大投入,除了提供对应算法理论的函数与模块,并利用自动代码生成实现“即插即用”外,在软件帮助文档中,各行业的应用案例也在逐步丰富中,帮助用户能够缩短学习曲线,尽快上手。如果您有相关方面的应用需求,也欢迎随时与我们联系!
审核编辑:郭婷
-
传感器
+关注
关注
2553文章
51527浏览量
757391 -
控制器
+关注
关注
113文章
16498浏览量
179869 -
PID
+关注
关注
36文章
1473浏览量
85956
原文标题:让控制器变“聪明” —— Simulink 自适应控制探讨
文章出处:【微信号:MATLAB,微信公众号:MATLAB】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
AMD Versal自适应SoC器件Advanced Flow概览(下)
基于自适应优化的高速交叉矩阵设计
AMD Versal自适应SoC器件Advanced Flow概览(上)

英特尔与Stellantis Motorsports携手推进自适应控制技术
自适应电流焊接控制器:精准调控,高效焊接
空间光调制器自适应激光光束整形
步进电机如何自适应控制?步进电机如何细分驱动控制?
ALINX受邀参加AMD自适应计算峰会
如何在自己的固件中增加wifi自适应性相关功能,以通过wifi自适应认证测试?
基于非线性自适应学习控制器的四轴飞行器避障方案
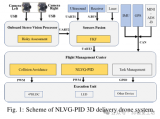




 Simulink Control Design对于自适应控制理论的支持
Simulink Control Design对于自适应控制理论的支持
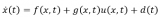











评论