FIR、IIR滤波器的FPGA实现和仿真研究分析

IIR滤波器设计

(一)冲激响应不变法

这种方法是通过将模拟滤波器频率特性H(s)反拉氏变换为h(t)，再将h(t)等间隔抽样成h(n)后，对h(n)取Z变换求得H(z)，即得到了数字滤波器的系统函数。

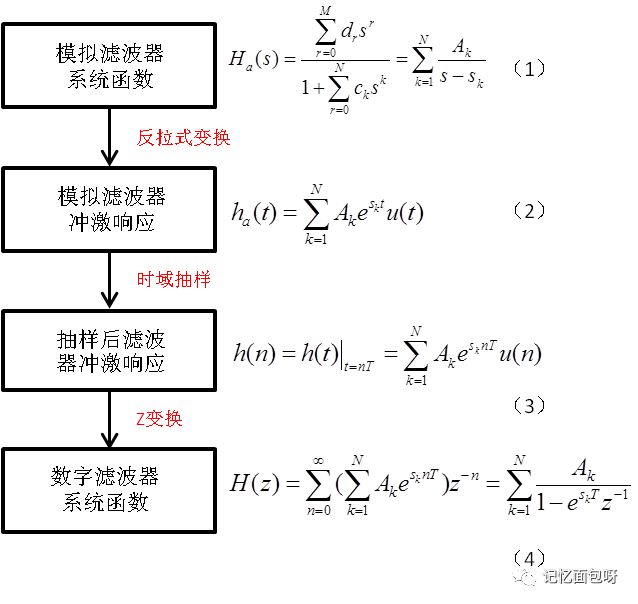
对比(1)式和(4)式可以发现S域中的极点s映射到Z域，则位于z=e^(sT)处。

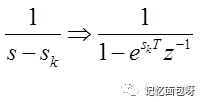
由映射关系可知z平面与s平面呈多值映射的关系。

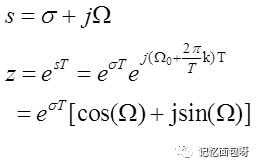
s平面的虚轴对应的σ=0，则上式中第一项e^(σT)=1，第二项表示旋转的角度，角度以2π/T为周期，所以s平面的虚轴每段2π/T都对应z平面上的单位圆。

s左平面对应σ<0，即第一项e^(σT)<1,所以s域的左半平面对应z平面上的单位圆内。

s右平面对应σ>0，即第一项e^(σT)>1,所以s域的右半平面对应z平面上的单位圆外。

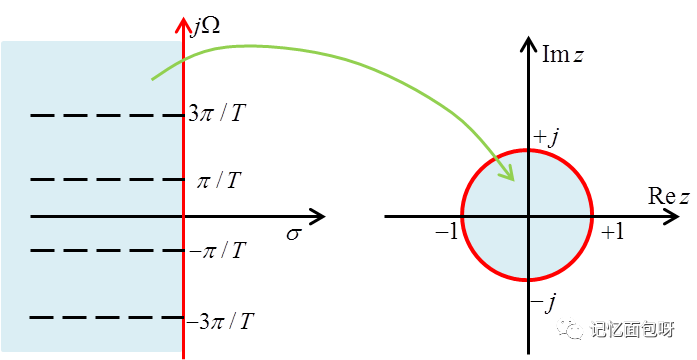
在第二步中，我们对h(t)进行了抽样，对应到S域则会产生频谱沿虚轴以2π/T为周期的搬移。

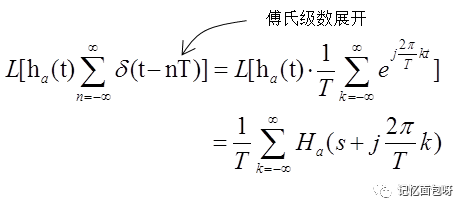
所以实际上我们得到的是h(t)抽样后的S平面与Z平面的映射，当Ω以2π/T整数倍改变时，会映射到Z平面上同一点。下图所示为s平面虚轴映射到z平面的单位圆。可以看出产生了频谱混叠现象。

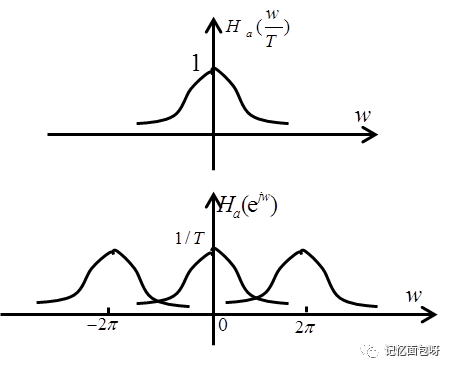
综上，冲激响应不变法可以将模拟滤波器转换成数字滤波器，但由于混叠现象使得高频部分严重失真，因而只适用于低通滤波器或限带(0<Ω<π)的高通或带通场合。

(二)双线性变换法

上面的冲激响应不变法的缺点就是会产生频谱混叠，究其原因是由于对信号进行了抽样，实际得到的是周期延拓后的S平面与Z平面的映射，所以产生了多值映射。

在双线性变换法中，我们首先将S平面通过反正切函数压缩到S1平面的(-π/T,π/T)横带内，再使用上面冲激响应不变法中使用的平面映射关系Z=e^(s1T)，将S1平面映射到Z平面。这样一来S平面与Z平面就构成了单值映射的关系。

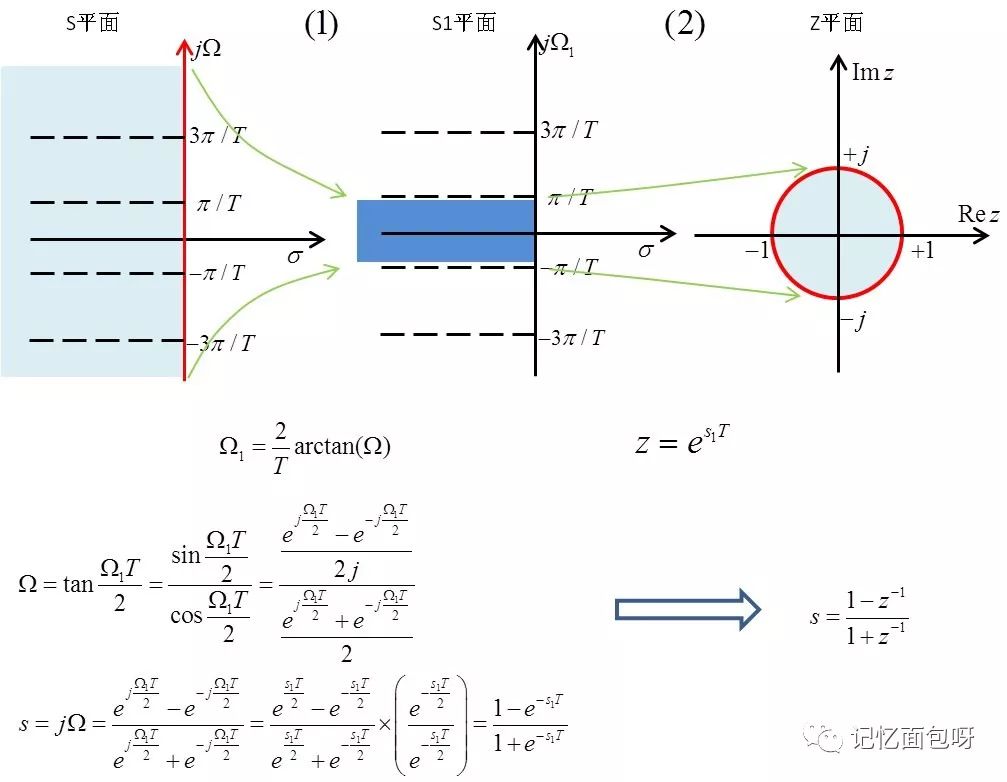
第二步由S1平面映射至Z平面时，使用了z=e^(s1T)，和冲激响应不变法中S到Z平面使用的映射一样，应该相当于用了冲激响应不变法，进行了一次频谱延拓再映射到Z平面吧。延拓后S1平面到Z平面是多值映射，但S平面到Z平面是单值映射。S平面整个虚轴对应于Z平面的单位圆一周。

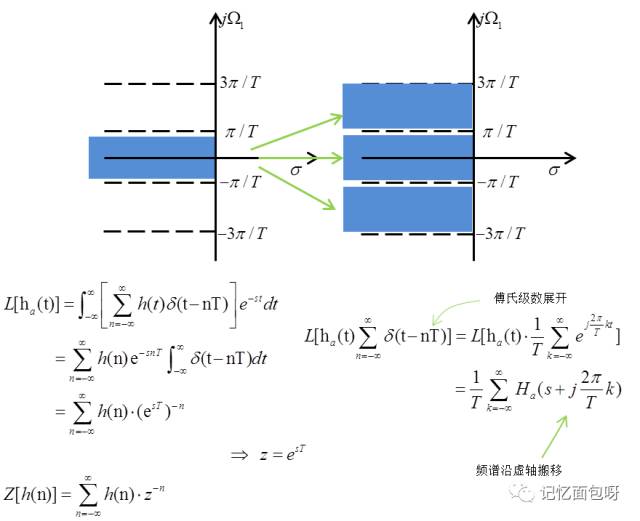
综上，双线性变换法克服了多值映射关系，可以消除频率的混叠。但是由于Ω与w成非线性关系，频率有畸变。

FIR滤波器设计

FIR滤波器的设计比较简单，就是要设计一个数字滤波器去逼近一个理想的低通滤波器。通常这个理想的低通滤波器在频域上是一个矩形窗。

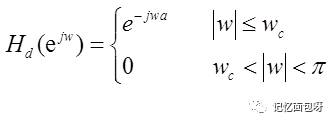
但是在时域上它是一个Sa函数。但是这个采样序列是无限的，计算机是无法对它进行计算。

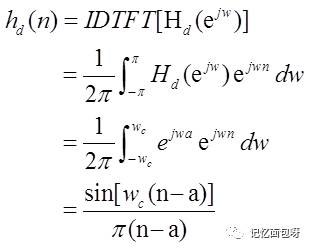
故我们需要对此采样函数进行截断处理。也就是把这个时域采样序列去乘一个窗函数，也就是加一个窗函数。

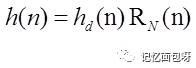
就把这个无限的时域采样序列截成了有限个序列值。

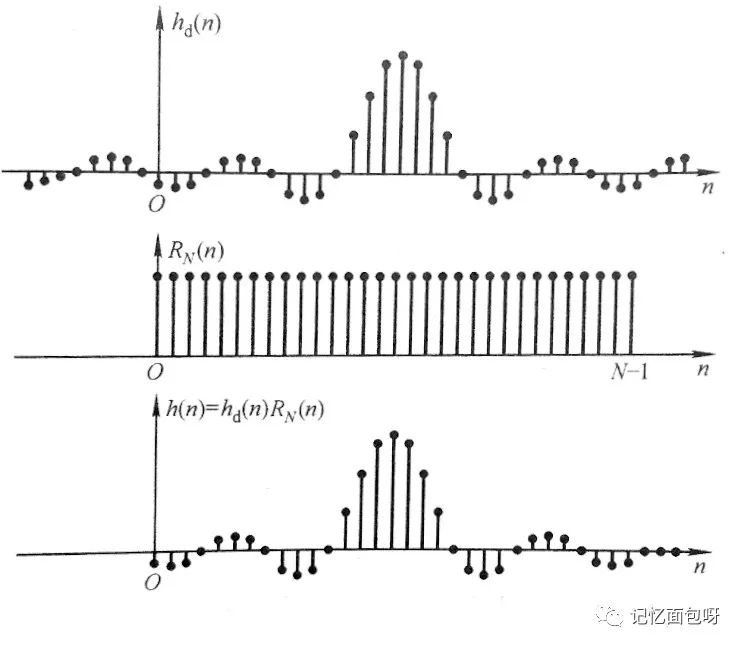
但是加窗后对此采样序列的频域也产生了影响：此时的频域便不在是一个理想的矩形窗，而是成了一个有过渡带，阻带有波动的低通滤波器。

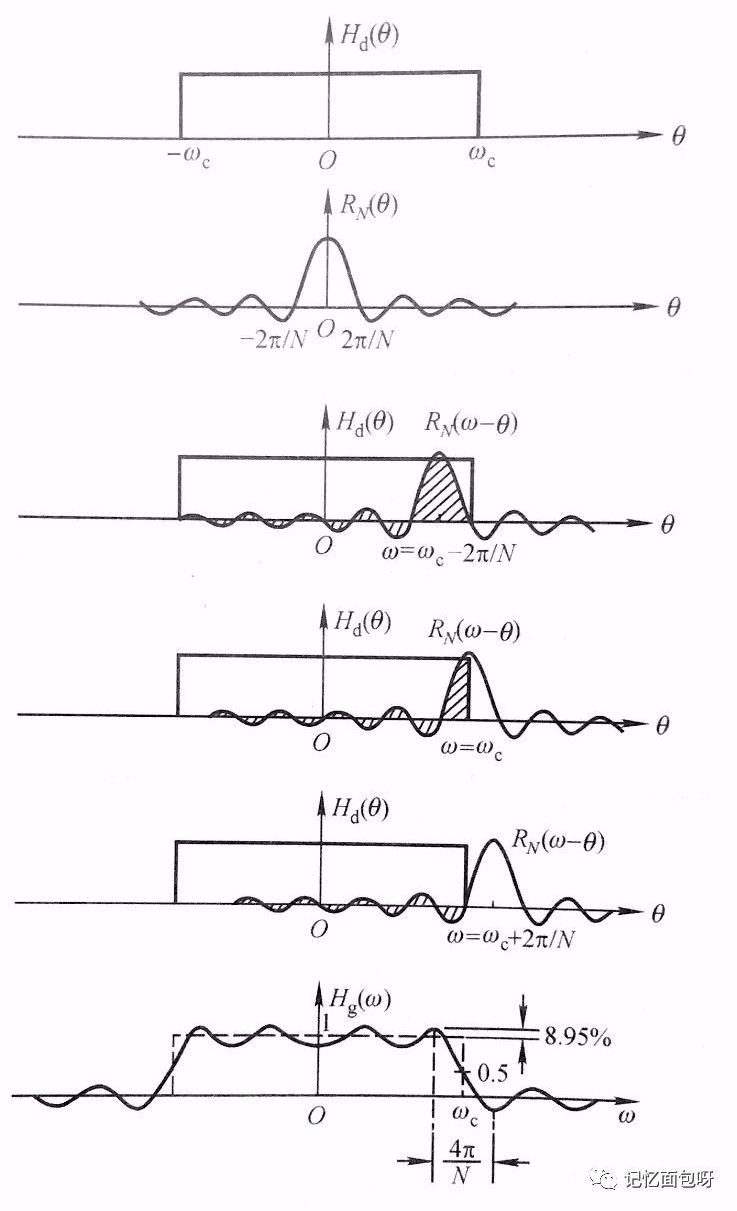
通常根据所加的窗函数的不同，在频域所得的低通滤波器的阻带衰减也不同。常用的窗函数有矩形窗、三角窗、汉宁窗（升余弦窗）、BLACKMAN窗（二阶升余弦窗）等。

所以窗函数法设计FIR滤波器的步骤如下：

FIR滤波器的FPGA实现

由于在Quartus中提供了FIR滤波器的IP核，所以只需要利用MATLAB根据要求计算出滤波器的系数，再将系数导入IP核就可以实现FIR滤波器。

要求：滤波器采样频率8MHz，过渡带[1MHz,2MHz]，通带衰减小于1dB，阻带衰减大于40dB，滤波器系数量化位数为12比特。

1.利用MATLAB设计出满足要求的FIR滤波器

这里需要用到kaiserord函数得到满足要求的最小阶数，及firpm函数设计最优滤波器。下面的代码参考自《数字调制解调技术的MATLAB与FPGA实现》杜勇。

matlab代码(可以滑动哟)

%E4_5_LpfDesign.m

%设计一个低通滤波器。采样频率fs=8MHz,过渡带fc=[1MHz 2MHz]；

%绘出滤波器第数量化前后的幅频响应图；将量化后的滤波器系数写入指定的txt文本文件中

function h_pm=E4_5_LpfDesign;

fs=8*10^6; %采样频率

qm=12; %滤波器系数量化位数

fc=[1*10^6 2*10^6]; %过渡带

mag=[1 0]; %窗函数的理想滤波器幅度

%设置通带容限a1及阻带容限a2

%通带衰减ap=-20*log10(1-a1)=0.915dB,阻带衰减为as=-20*log10(a2)=40dB

a1=0.1;a2=0.01;

dev=[a1 a2];

%采用凯塞窗函数获取满足要求的最小滤波器阶数

[n,wn,beta,ftype]=kaiserord(fc,mag,dev,fs)

%采用firpm函数设计最优滤波器

fpm=[0 fc(1)*2/fs fc(2)*2/fs 1]; %firpm函数的频段向量

magpm=[1 1 0 0]; %firpm函数的幅值向量

h_pm=firpm(n,fpm,magpm); %设计最优滤波器

%量化滤波系数

q_pm=round(h_pm/max(abs(h_pm))*(2^(qm-1)-1));

%将生成的滤波器系数数据写入FPGA所需的txt文件中

fid=fopen('E:FPGA DOCFPGA数字信号处理数字调制解调技术的MATLAB与FPGA实现——AlteraVerilog版Chapter_4E4_5_FirIpCoreE4_5_lpf.txt','w');

fprintf(fid,'%12.12f ',h_pm);

fclose(fid);

2.调用FIR滤波器IP核

设置FIR参数时，设置滤波器系数位宽为12比特；流水线级数为1；实现结构设置为Multi-Cycle(多时钟周期结构)，FPGA系统时钟频率为32MHz,而数据速率为8MHz，所以每4个时钟周期处理一个数据即可，因此设置“Clock to compute”的值为4。在设置滤波器系数的时候，将设计好的TXT文件装载进去，生成完IP核后将其例化。

顶层模块

module FirIPCore (

reset_n,clk,Xin,

Yout);

inputreset_n; //复位信号，低电平有效

inputclk; //FPGA系统时钟/数据速率：32MHz

input signed [11:0]Xin; //数据输入频率为8MHZ

output signed [24:0]Yout; //滤波后的输出数据

wire sink_valid,ast_source_ready,ast_source_valid,ast_sink_ready;

wire [1:0] ast_source_error;

wire [1:0] ast_sink_error;

assign ast_source_ready=1'b1;

assign ast_sink_error=2'd0;

//由于系统时钟为数据速率的4倍，因此需要每4个时钟周期设置一次ast_sink_valid有效信号

reg [1:0] count;

reg ast_sink_valid;

always @(posedge clk or negedge reset_n)

if (!reset_n) begin

count <= 2'd0;

ast_sink_valid <= 1'b0;

end

else begin

count <= count + 2'd1;

if (count==0)

ast_sink_valid <= 1'b1;

else

ast_sink_valid <= 1'b0;

end

assign sink_valid = ast_sink_valid;

//实例化fir滤波器核

firu0(

.clk(clk),

.reset_n(reset_n),

.ast_sink_data(Xin),

.ast_sink_valid(sink_valid),

.ast_source_ready(ast_source_ready),

.ast_sink_error(ast_sink_error),

.ast_source_data(Yout),

.ast_sink_ready(ast_sink_ready),

.ast_source_valid(ast_source_valid),

.ast_source_error(ast_source_error));

endmodule

3.MATLAB产生仿真测试数据

由于设计的时截止频率为2MHz的低通滤波器，我们可以产生频率为1MHz和2MHz的合成信号。

产生测试数据

%E4_6_TestData.M

f1=1*10^6; %信号1频率为1MHz

f2=2.1*10^6; %信号2频率为2.1MHz

Fs=8*10^6; %采样频率为8MHz

N=12; %量化位数为12比特

Len=2000; %数据长度为2000

%%产生两个单载波合成后的信号

t=0:1/Fs:(Len-1)/Fs;

c1=2*pi*f1*t;

c2=2*pi*f2*t;

s1=sin(c1);%产生正弦波

s2=sin(c2);%产生正弦波

s=s1+s2; %对两个单载波信号进行合成

%调用E4_6_LpfDesign函数设计的滤波器对信号进行滤波

hn=E4_5_LpfDesign;

Filter_s=filter(hn,1,s);

%求信号的幅频响应

m_s=20*log(abs(fft(s,1024)))/log(10); m_s=m_s-max(m_s);

%滤波后的幅频响应

Fm_s=20*log(abs(fft(Filter_s,1024)))/log(10); Fm_s=Fm_s-max(Fm_s);

%滤波器本身的幅频响应

m_hn=20*log(abs(fft(hn,1024)))/log(10); m_hn=m_hn-max(m_hn);

%设置幅频响应的横坐标单位为Hz

x_f=[0:(Fs/length(m_s)):Fs/2];

%只显示正频率部分的幅频响应

mf_s=m_s(1:length(x_f));

Fmf_s=Fm_s(1:length(x_f));

Fm_hn=m_hn(1:length(x_f));

%绘制幅频响应曲线

subplot(211)

plot(x_f,mf_s,'-.',x_f,Fmf_s,'-',x_f,Fm_hn,'--');

xlabel('频率(Hz)');ylabel('幅度(dB)');title('Matlab仿真合成单频信号滤波前后的频谱');

legend('输入信号频谱','输出信号频谱','滤波器响应');

grid;

%绘制滤波前后的时域波形

subplot(212)

%绘制时域波形

%设置显示数据范围，设置横坐标单位ms

t=0:1/Fs:80/Fs;t=t*10^6;

t_s=s(1:length(t));

t_filter_s=Filter_s(1:length(t));

plot(t,t_s,'--',t,t_filter_s,'-');

xlabel('时间(ms)');ylabel('幅度');title('FPGA仿真合成单频信号滤波前后的时域波形');

legend('输入信号波形','输出信号波形');

grid;

%对仿真产生的合成单频信号进行量化处理

s=s/max(abs(s)); %归一化处理

Q_s=round(s*(2^(N-1)-1));%12比特量化

%将生成的数据以二进制数据格式写入txt文件中

fid=fopen('E:FPGA DOCFPGA数字信号处理数字调制解调技术的MATLAB与FPGA实现——AlteraVerilog版Chapter_4E4_5_FirIpCoreE4_5_TestData.txt','w');

for i=1:length(Q_s)

B_noise=dec2bin(Q_s(i)+(Q_s(i)<0)*2^N,N);

for j=1:N

if B_noise(j)=='1'

tb=1;

else

tb=0;

end

fprintf(fid,'%d',tb);

end

fprintf(fid,' ');

end

fprintf(fid,';');

fclose(fid);

4.编写测试激励文件

测试激励文件

`timescale 1 ns/ 1 ns

module FirIPCore_vlg_tst();

reg [11:0] Xin;

reg clk,clk_data;

reg reset_n;

wire [24:0] Yout;

FirIPCore i1 (

.Xin(Xin),

.Yout(Yout),

.clk(clk),

.reset_n(reset_n)

);

parameter clk_period=20; //设置时钟信号周期（频率）:50MHz

parameter data_clk_period=clk_period*4; //设置数据时钟周期

parameter clk_half_period=clk_period/2;

parameter data_half_period=data_clk_period/2;

parameter data_num=2000; //仿真数据长度

parameter time_sim=data_num*data_clk_period; //仿真时间

initial

begin

//设置输入信号初值

Xin=12'd10;

//设置时钟信号初值

clk=1;

clk_data=1;

//设置复位信号

reset_n=0;

#110 reset_n=1;

//设置仿真时间

#time_sim $finish;

end

//产生时钟信号

always

#clk_half_period clk=~clk;

always

#data_half_period clk_data=~clk_data;

//从外部TX文件(E4_5_TestData.txt)读入数据作为测试激励

integer Pattern;

reg [11:0] stimulus[1:data_num];

initial

begin

//文件必须放置在"工程目录simulationmodelsim"路径下

$readmemb("E4_5_TestData.txt",stimulus);

Pattern=0;

repeat(data_num)

begin

Pattern=Pattern+1;

Xin=stimulus[Pattern];

#data_clk_period;

end

end

//将仿真数据Yout写入外部TXT文件中(E4_5_FpgaData.txt)

integer file_out;

initial

begin

//文件放置在"工程目录simulationmodelsim"路径下

file_out = $fopen("E4_5_FpgaData.txt");

if(!file_out)

begin

$display("could not open file!");

$finish;

end

end

wire rst_write;

wire signed [24:0] dout_s;

assign dout_s = Yout; //将Yout转换成有符号数据

assign rst_write = clk_data & (reset_n); //产生写入时钟信号，复位状态时不写入数据

always @(posedge rst_write )

$fdisplay(file_out,"%d",dout_s);

endmodule

仿真结果

IIR滤波器的FPGA实现

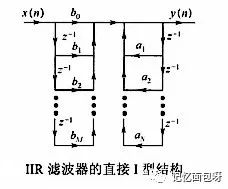
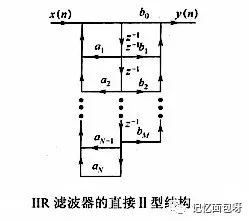
IIR滤波器结构包括直接Ⅰ型、直接Ⅱ型、级联型和并联型。其中级联型结构便于准确实现数字滤波器零极点，且受参数量化影响小，因此使用广泛。

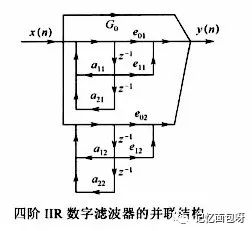
它实际上相当于将级数较多的滤波器分解成多个级数小于等于3的IIR滤波器，前一级的输出作为后一级的输入，其中每个滤波器均可看成独立的结构。

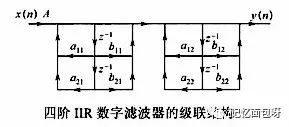
同样滤波器的参数需要使用matlab计算出，还需要将计算出的滤波器参数转换成级联的形式。

由于没有现成的IIR滤波器IP核，所以需要用verilog来实现，结构如下。可以看出用FPGA实现并不复杂，只是移位乘上系数相加的过程。

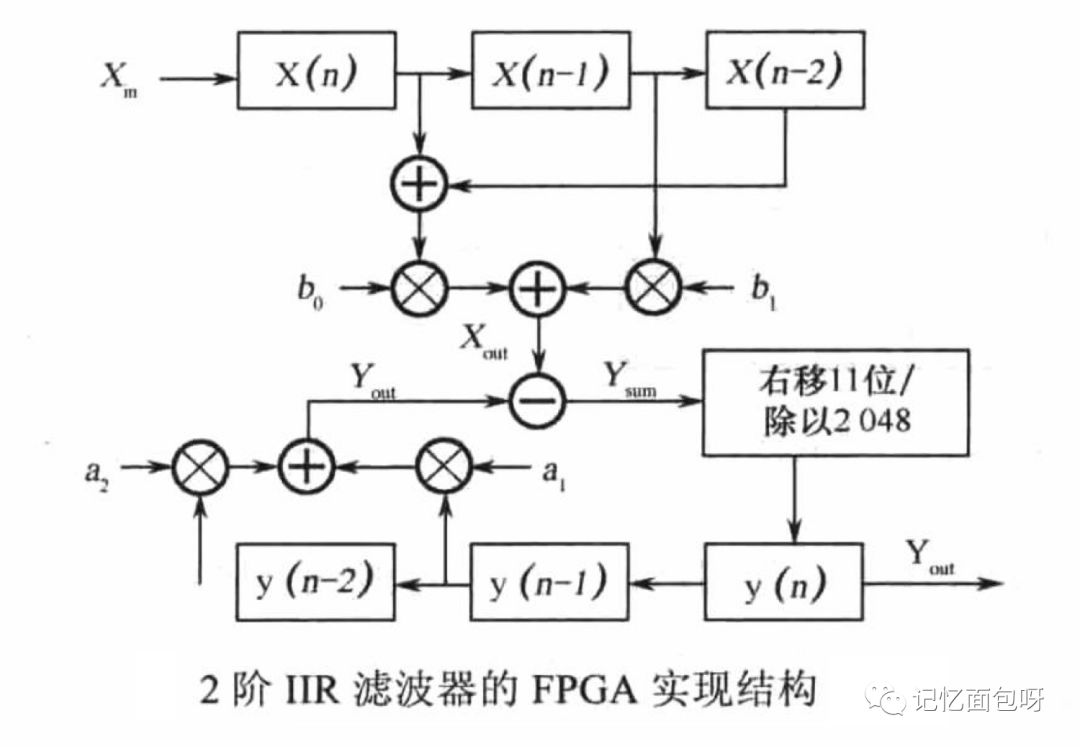
部分代码如下

IIR第一级

module FirstTap (

rst,clk,Xin,

Yout);

inputrst; //复位信号，高电平有效

inputclk; //FPGA系统时钟，频率为2kHz

input signed [11:0]Xin; //数据输入频率为2kHZ

output signed [11:0]Yout; //滤波后的输出数据

//零点系数的实现代码/////////////////////////

//将输入数据存入移位寄存器中

reg signed[11:0] Xin1,Xin2;

always @(posedge clk or posedge rst)

if (rst)

//初始化寄存器值为0

begin

Xin1 <= 12'd0;

Xin2 <= 12'd0;

end

else

begin

Xin1 <= Xin;

Xin2 <= Xin1;

end

//采用移位运算及加法运算实现乘法运算

wire signed [23:0] XMult0,XMult1,XMult2;

assign XMult0 = {{6{Xin[11]}},Xin,6'd0}+{{7{Xin[11]}},Xin,5'd0}-{{11{Xin[11]}},Xin,1'd0}; //*94

assign XMult1 = {{5{Xin1[11]}},Xin1,7'd0}+{{9{Xin1[11]}},Xin1,3'd0}+{{10{Xin1[11]}},Xin1,2'd0}; //*140

assign XMult2 = {{6{Xin2[11]}},Xin2,6'd0}+{{7{Xin2[11]}},Xin2,5'd0}-{{11{Xin2[11]}},Xin2,1'd0}; //*94

//对滤波器系数与输入数据乘法结果进行累加

wire signed [23:0] Xout;

assign Xout = XMult0 + XMult1 + XMult2;

//极点系数的实现代码///////////////////////

wire signed[11:0] Yin;

reg signed[11:0] Yin1,Yin2;

always @(posedge clk or posedge rst)

if (rst)

//初始化寄存器值为0

begin

Yin1 <= 12'd0;

Yin2 <= 12'd0;

end

else

begin

Yin1 <= Yin;

Yin2 <= Yin1;

end

//采用移位运算及加法运算实现乘法运算

wire signed [23:0] YMult1,YMult2;

wire signed [23:0] Ysum,Ydiv;

assign YMult1 = {{2{Yin1[11]}},Yin1,10'd0}+{{5{Yin1[11]}},Yin1,7'd0}+{{6{Yin1[11]}},Yin1,6'd0}-

{{11{Yin1[11]}},Yin1,1'd0}-{{12{Yin1[11]}},Yin1}; //*1213=1024+128+64-2-1

assign YMult2 = {{4{Yin2[11]}},Yin2,8'd0}+{{9{Yin2[11]}},Yin2,3'd0}+{{10{Yin2[11]}},Yin2,2'd0}; //*268=256+8+4

//第一级IIR滤波器实现代码///////////////////////////

assign Ysum = Xout+YMult1-YMult2;

assign Ydiv = {{11{Ysum[23]}},Ysum[23:11]};//2048

//根据仿真结果可知，第一级滤波器的输出范围可用9位表示

assign Yin = (rst ? 12'd0 : Ydiv[11:0]);

//增加一级寄存器，提高运行速度

reg signed [11:0] Yout_reg ;

always @(posedge clk)

Yout_reg <= Yin;

assign Yout = Yout_reg;

endmodule

仿真结果

审核编辑：郭婷