一种使用Python分析混合模式信号链中噪声的简单方法

作者：Mark ThorenandCristina Șuteu

任何涉及物理世界灵敏测量的应用都始于精确、精密和低噪声信号链。现代、高度集成的数据采集设备通常可以直接连接到传感器输出，在单个硅器件上执行模拟信号调理、数字化和数字滤波，从而大大简化了系统电子元件。然而，仍然需要全面了解信号链的噪声源和噪声限制滤波器，才能从这些现代器件中提取最大性能并进行调试。

介绍

本教程是转换器连接教程的延续。1,2它将专注于单个信号链元件的噪声，并使用Python/SciPy对其进行建模。3和LTspice。然后，它将通过使用Python通过libm2k和Linux工业输入输出（IIO）框架驱动ADALM2000多功能USB测试仪器来验证结果。所有源代码和其他讨论均可在配套的主动学习实验室练习中找到。®®

混合模式信号链无处不在。简而言之，任何将真实信号转换为电表示然后数字化的系统都可以归类为混合模式信号链。在链条上的每个点，信号都会以各种方式降级，通常可以表征为某种形式的失真或附加噪声。一旦进入数字领域，数字化数据的处理也不是完美的，但至少出于所有实际目的，它不受许多影响模拟信号的因素的影响——元件容差、温度漂移、来自相邻信号的干扰或电源电压变化。

随着行业不断突破物理极限，有一点是肯定的：仪器仪表的模拟和混合信号组件总是有改进的余地。如果市场上出现模数转换器（ADC）或数模转换器（DAC），在速度，噪声，功率，精度或价格方面处于领先地位，制造商将很乐意将其应用于现有问题，然后要求更多改进。然而，为了为您的应用实现最佳的采集系统，了解组件的局限性并相应地选择它们是至关重要的。

通用混合模式信号链

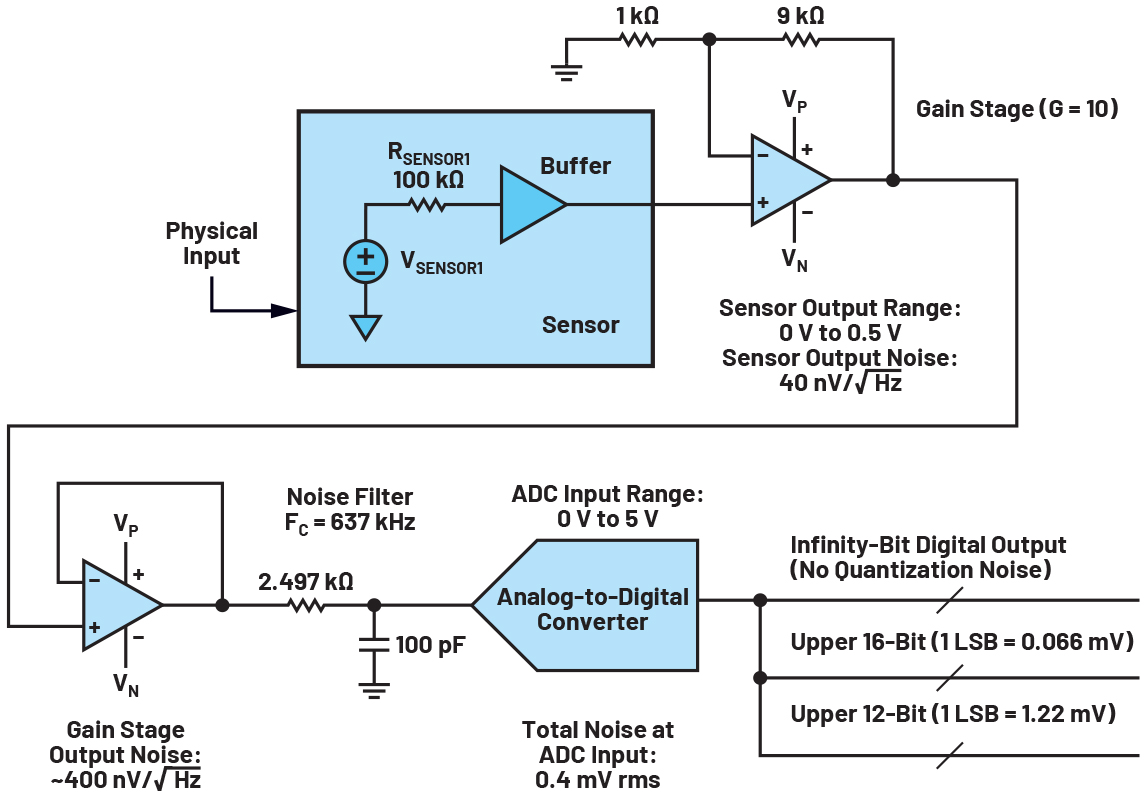
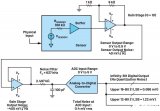
图1显示了精密仪器仪表应用的典型通用信号链，具有物理输入和数字输出。有许多关于ADC的背景参考资料可用，4大多数读者会感觉到ADC在某个时间点对输入信号进行采样（或测量信号在某个观察时间内的平均值），并生成该信号的数值表示形式 - 通常是二进制数，其值介于0到2之间（N – 1）其中 N 是输出字中的位数。

图1.在混合模式信号链中，温度、光强度、pH、力或扭矩等一些物理现象被转换为电参数（电阻、电流或直接转换为电压）。然后，该信号被放大、低通滤波，并由ADC数字化，其中可能包括内部数字滤波。

模数转换器噪声源

虽然图1中有几个噪声源，但ADC数字输出中的位数经常被忽略或过分强调。从历史上看，ADC的位数被认为是最终品质因数，其中16位转换器被认为比14位转换器好4倍。5但在现代高分辨率转换器的情况下，位数可以安全地忽略不计。注意信号链设计的一般原则：

“一级的输入噪声应略低于前一级的输出噪声。

与任何信号链一样，ADC内的一个噪声源通常占主导地位。因此，如果将无噪声信号施加到N位ADC：

产生单个输出代码或两个相邻输出代码，则量化噪声占主导地位。信噪比（SNR）不能大于（6.02 N + 1.76）dB。6

导致许多输出代码的高斯分布，然后热噪声源占主导地位。信噪比不大于：

哪里：

V在（p-p） 是满量程输入信号。
σ是以电压单位表示的输出代码的标准偏差。

超高分辨率转换器，如稍后将用作示例的AD7124-8，很少受到量化噪声的限制;热噪声在所有增益/带宽设置中占主导地位，短路输入将始终产生相当高斯的输出代码分布。图2显示了24位Σ-Δ型ADC7124-8的接地输入直方图，内部可编程增益放大器（PGA）分别设置为1和128。

图2.PGA增益为1（左）时，AD7124输出噪声表示13个代码，标准偏差约为2.5个代码。虽然量化是可见的，但热噪声更为显著。PGA增益为128（右）时，表示187个代码，量化噪声微不足道。截断一个或两个最低有效位（加倍或四倍量化噪声）不会导致信息丢失。

建模和测量ADC噪声

对热噪声受限ADC的噪声进行建模非常简单。如果噪声“表现良好”（如图2所示为高斯噪声）且在整个ADC输入范围内恒定，则可以使用NumPy的7随机正态函数，然后通过取标准差进行验证，如图3所示。

图3.使用 NumPy 对高斯噪声进行建模。

图4.ADALM2000是一款多功能USB测试仪器，具有两个通用模拟输入和两个输出，采样速率分别为100 MSPS和150 MSPS。它可以用作测量ADC噪声带宽和滤波器响应的简单信号源。运行内核的Raspberry Pi 4支持AD7124器件驱动程序，充当AD7124和主机之间的简单桥梁。

AD7124器件驱动程序属于行业标准IIO框架，该框架具有完善的软件API（包括Python绑定）。应用程序代码可以在本地（在树莓派上）或通过网络、串行或 USB 连接在远程机器上运行。此外，皮亚迪-伊奥8抽象层负责与IIO设备接口所需的大部分样板设置，从而大大简化了软件界面。图5说明了如何打开与AD7124-8的连接，对其进行配置，捕获数据块，然后关闭连接。

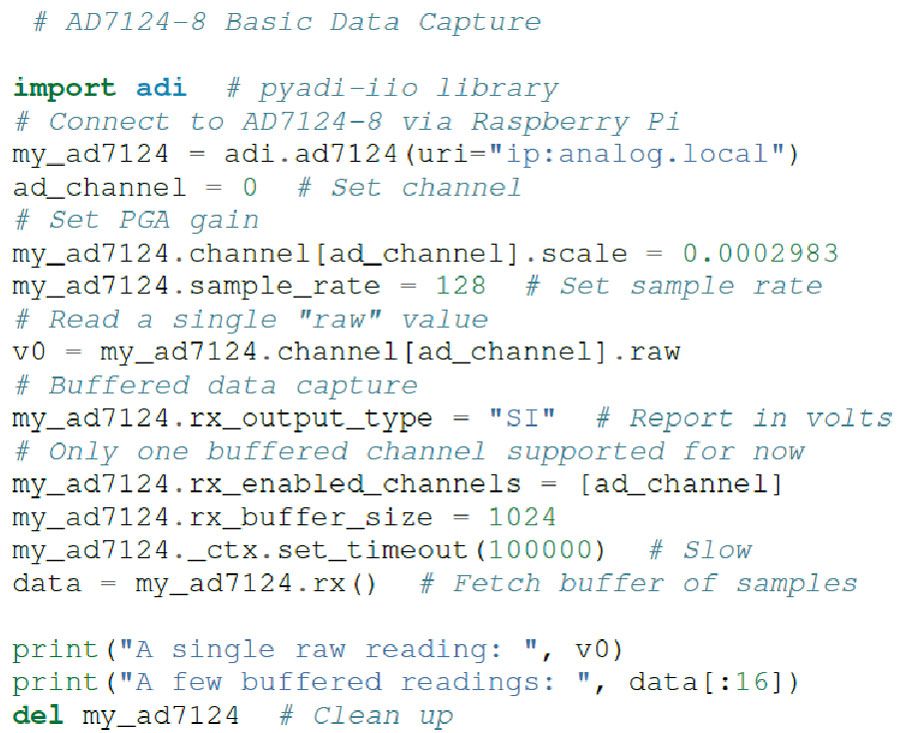
图5.AD7124-8基本数据采集。

建立与AD7124-8的通信后，可以执行一个非常简单但非常有用的测试：直接测量输入噪声。简单地将ADC的输入短路并查看ADC代码的分布是表征信号链设计的重要步骤。AD7124输入模式设置为单极性，因此只有正值有效;图6所示的测试电路确保输入始终为正。

图6.电阻分压器用于在AD7124-8的输入端产生1.25 mV偏置，克服了15 μV的最大失调电压，并确保ADC读数始终为正。

图 7 显示了两个 1024 点测量值。下部（蓝色）迹线是在最初通电后立即拍摄的。

图7.在施加1.25 mV偏置的情况下采集两个AD7124-8数据。下方的迹线显示了上电后电路预热时的初始漂移。上面的曲线显示半小时预热后读数稳定。

“漂移”可能是由于许多因素造成的——内部基准升温、外部电阻升温（因此漂移）或寄生热电偶，其中略有不同的金属在存在热梯度的情况下会产生电压。预热后的实测噪声约为565 nV rms，与数据手册中的噪声规格相当。

将ADC噪声表示为密度

模拟信号链设计的一般原理（一级的输入噪声应略低于前一级的输出噪声）如果所有元件都包含噪声密度规格，则计算起来很容易——大多数明确指定的传感器和几乎所有放大器都是如此。

与放大器和传感器不同，ADC数据手册通常不包括噪声密度规格。将ADC的噪声表示为密度，可以直接将其与模拟信号链中最后一个元件（可能是ADC驱动器级、增益级或传感器本身）输出端的噪声进行比较。

ADC的内部噪声必然出现在直流和采样速率的一半之间。理想情况下，这种噪声是平坦的，或者至少是可预测的形状。事实上，由于ADC的总噪声分布在已知带宽内，因此可以将其转换为噪声密度，可以直接与信号链中的其他元件进行比较。精密转换器通常直接给出总噪声，单位为伏特均方根：

其中 e有效值是总均方根噪声，根据接地输入代码直方图的标准偏差计算得出。

经过正弦信号测试和表征的高速转换器通常具有SNR规格。如果提供，总均方根噪声可以计算为：

其中ADCp-p是ADC的峰峰值输入范围。

然后可以计算等效噪声密度：

其中 fS是以样本/秒为单位的 ADC 采样速率。

预热后图7的总噪声为565 nV，数据速率为128 SPS。噪声密度约为：

ADC现在可以直接包含在信号链噪声分析中，从而为优化信号链增益提供了指南：

将增益增加到ADC之前最后一级的噪声密度略高于ADC的噪声密度，然后停止。不要再费心增加信号链增益了——你只是在放大噪声并减小允许的输入范围。

这与“填充”ADC输入范围的传统做法背道而驰。如果ADC的传递函数存在阶跃或不连续性，则使用ADC的更多输入范围可能会有所好处，但对于“表现良好”的ADC（大多数Σ-Δ型ADC和现代高分辨率逐次逼近寄存器（SAR）ADC），噪声优化是首选方法。

测量ADC滤波器响应

AD7124-8是一款Σ-Δ型ADC，其中调制器产生高采样速率但噪声（低分辨率）的模拟输入表示。然后，这些噪声数据由内部数字滤波器滤波，产生较低速率、较低噪声的输出。滤波器的类型因ADC而异，具体取决于预期的最终应用。AD7124-8为通用型器件，面向精密应用。因此，数字滤波器响应和输出数据速率是高度可配置的。虽然滤波器响应在数据手册中有明确定义，但有时可能需要测量滤波器对给定信号的影响。AD7124-8滤波器响应代码模块（见图9）通过向ADC输入施加正弦波并分析输出来测量滤波器响应。这种方法可以很容易地适应于测量其他波形——小波和模拟的物理事件。ADALM2000连接到AD7124-8电路，如图8所示。

图8.ADALM2000波形发生器用于产生一系列正弦波频率，允许直接测量AD7124-8的滤波器响应。脚本将正弦波幅度和失调设置为安全电平，而1 kΩ电阻可在发生故障时保护AD7124-8。（ADALM2000输出电压范围为–5 V至+5 V，而AD7124-8的绝对最大限值为–0.3 V和+3.6 V。

AD7124-8滤波器响应代码模块（见图9）将ADALM2000的波形发生器设置为产生10 Hz的正弦波，捕获1024个数据点，计算均方根值，然后将结果附加到列表中。send_sinewave和capture_data是实用程序函数，分别向ADALM2000发送正弦波并从AD7124接收数据块。2然后，它将逐步通过高达120 Hz的频率，然后绘制结果，如图10所示。

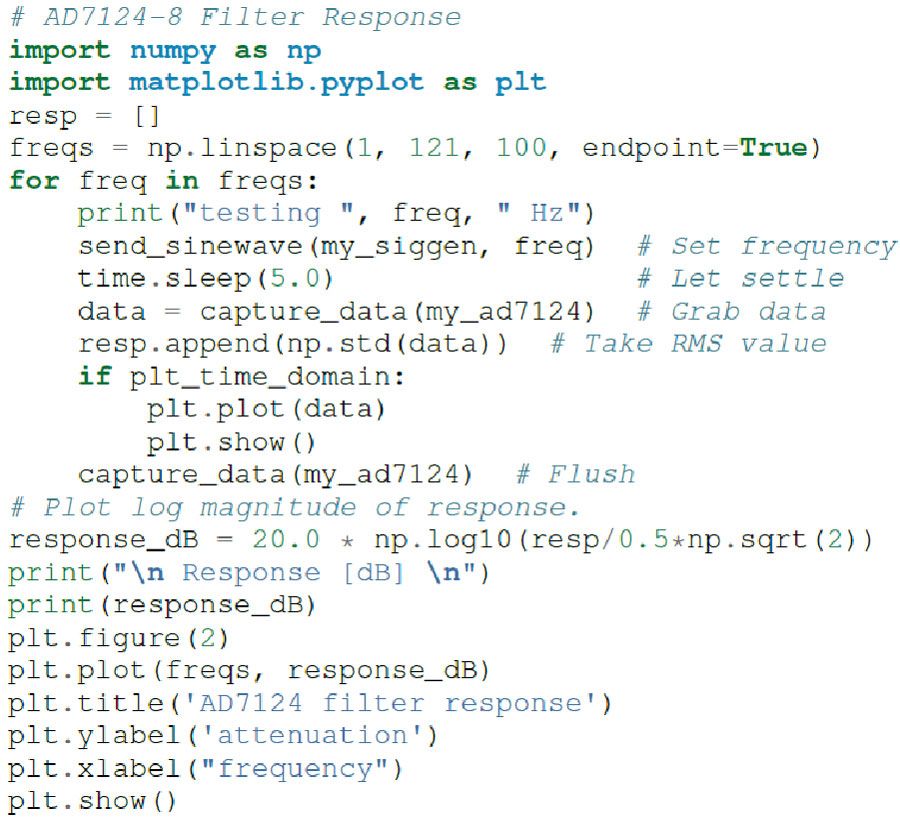
图9.ADALM2000的滤波器响应模块程序。

图 10.AD7124滤波器在64 SPS、sinc4模式下的响应测量结果显示了滤波器的通带、第一个波瓣和前两个零点。

虽然测量高衰减值需要更安静、更低失真的信号发生器，但这种设置可以明显地显示前几个主要波瓣的响应。

ADC滤波器建模

测量ADC滤波器响应的能力是台架验证的实用工具。但是，为了完全仿真信号链，需要滤波器的模型。许多转换器（包括AD7124-8）没有明确提供这一点，但可以根据数据手册中提供的信息对可行的模型进行逆向工程。

请注意，以下仅为AD7124-8滤波器的型号;它不是位精确的表示形式。有关所有保证参数，请参考AD7124-8数据手册。

AD7124的滤波器均具有各种sinc功能组合的频率响应（频率响应与（sin{f}/f）成比例）N).这些过滤器相当容易构造，并且在已知空值时进行逆向工程。

图11显示了AD7124-8的10 Hz陷波滤波器。还提供高阶 sinc3 和 sinc4 过滤器的各种组合。

图 11.AD7124-8 10 Hz陷波滤波器具有sinc1幅度响应;滤波器的脉冲响应只是100 ms时间间隔内样本的未加权（矩形）平均值。

图12所示的同步50 Hz/60 Hz抑制滤波器就是一个简单的例子。该滤波器旨在强烈抑制来自交流电源线的噪声，即50 Hz（如欧洲）或60 Hz（如美国）。

图 12.AD7124-8 50 Hz/60 Hz抑制滤波器响应是50 Hz、sinc3滤波器和60 Hz、sinc1滤波器的组合。

高阶sinc滤波器可以通过卷积sinc1滤波器生成。例如，卷积两个sinc1滤波器（在时间上具有矩形脉冲响应）将产生三角脉冲响应和相应的sinc2频率响应。AD7124滤波器代码块（见图13）生成一个在50 Hz时为零的sinc3滤波器，然后在60 Hz时添加第四个为零的滤波器。

图 13.AD7124-8 50 Hz/60 Hz sinc滤波器的代码示例

滤波器产生的脉冲（时域）形状如图14所示。滤波器系数（抽头）值归一化，在零频率下获得单位（0 dB）增益。

图 14.反复卷积矩形脉冲响应会产生三角形，然后是类似高斯的脉冲响应。

最后，可以使用NumPy的freqz函数计算频率响应，如图16所示。响应如图 15 所示。

图 15.将 sinc3、50 Hz 陷波滤波器与 sinc1、60 Hz 滤波器卷积会产生强烈抑制 50 Hz 和 60 Hz 的复合响应。

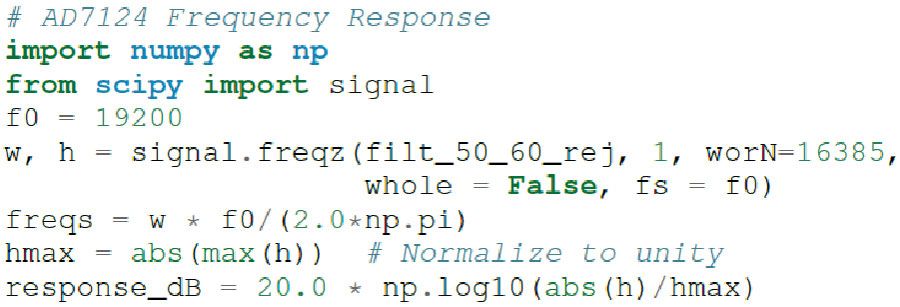
图 16.AD7124-8代码示例，用于sinc3 50 Hz陷波滤波器，带sinc 60 Hz滤波器。

电阻是徒劳的：传感器的基本限制

所有传感器，无论多么完美，都有一些最大输入值（以及相应的最大输出，可能是电压、电流、电阻，甚至拨号位置）和有限的本底噪声——即使输入完全静止，也存在输出“摆动”。在某些时候，具有电输出的传感器将包括一个具有有限电阻（或更一般地说，阻抗）的元件，由R表示传感器在图 17 中。这代表了一个无法改进的基本噪声限值——该电阻至少会产生 en（RMS） 伏特噪声：

哪里：

eN（RMS） 是总噪声。

K 是玻尔兹曼常数 （1.38E-23J/K）。

T 是电阻器的绝对温度（开尔文）。

F2 和 F1 是感兴趣频段的上限和下限。

将带宽归一化为 1 Hz 表示噪声密度（以 V/√Hz为单位）。

图 17.传感器通常包括一个内部缓冲器，以简化与下游电路的连接。虽然输出阻抗较低（通常接近0 Ω），但来自高阻抗检测元件的噪声与信号一起缓冲。

将带宽归一化为 1 Hz 表示噪声密度（以 V/√Hz为单位）。

传感器的数据手册可能规定低输出阻抗（通常接近0 Ω），但这可能是一个缓冲级，它简化了与下游电路的接口，但不能消除信号链早期阻抗引起的噪声。

还有许多其他传感器限制 - 机械，化学，光学 - 每个都有自己的理论限制，其影响可以在以后建模和补偿。但噪音是不能做到的缺陷

实验室噪声源

经过校准的噪声发生器充当“世界上最差的传感器”，它模拟传感器的噪声而不实际感应到任何东西。这种发生器允许直接测量信号链对噪声的响应。图18所示电路使用1 MΩ电阻作为127 nV/√Hz（室温下）噪声源，精度和带宽为“正常”。虽然精度还可以，但这种方法有优点：

它基于第一原理，因此在某种意义上可以作为未校准的标准。

它确实是随机的，没有重复的模式。

OP482是一款超低偏置电流放大器，具有相应的低电流噪声和足够低的电压噪声，使得1 MΩ输入阻抗引起的噪声占主导地位。增益配置为2121，输出噪声为269 μV/√Hz。

图 18.1 MΩ电阻用作可预测的噪声源，然后通过低噪声运算放大器将其放大至可用电平。

使用ADALM2000 USB仪器，使用Scopy GUI的频谱分析仪验证噪声源，如图19所示。9

图 19.基于电阻的实验室噪声发生器的输出具有大约10 kHz的可用带宽。

在所示分析仪设置下，ADALM2000的本底噪声为40 μV/√Hz，远低于噪声源的269 μV/√Hz。

虽然 Scopy 对于单次目视测量很有用，但使用 SciPy 周期图功能可以轻松复制该功能。原始数据是使用 libm2k 从 ADALM2000 收集的10和 Python 绑定，经过最低限度的处理以删除 DC 内容（否则会泄漏到低频箱中）并缩放到 nV/√Hz。这种方法如图20所示，可以应用于任何数据采集模块，只要采样速率是固定的和已知的，并且数据可以格式化为电压矢量。

图 20.ADALM2000的Python噪声源测量代码。

我们现在配备了已知的噪声源和测量该噪声源的方法，这两种方法都可用于验证信号链。

LTspice中的信号链建模

LTspice®是一款免费提供的通用模拟电路仿真器，可应用于信号链设计。它可以执行瞬态分析、频域分析（AC 扫描）和噪声分析，其结果可以导出并使用 Python 合并到混合信号模型中。

图21显示了模拟噪声发生器的噪声仿真，与实验结果非常吻合。仿真使用了与OP482具有相似特性的运算放大器。

图 21.实验室噪声源的LTspice仿真显示，其可用带宽与测量电路大致相同。

图22的电路噪声对于模型来说相当微不足道，因为它在某些带宽（目标信号所在的带宽中）是恒定的，高于该带宽，它以大约一阶低通响应滚降。这种技术派上用场的地方是模拟非平坦本底噪声，无论是由于高阶模拟滤波，还是有源元件本身。典型的例子是自稳零放大器（如LTC2057）中经常存在的噪声山，如图23所示。

图 22.LTC2057的噪声密度在低频时是平坦的，峰值为50 kHz（内部振荡器100 kHz频率的一半）。

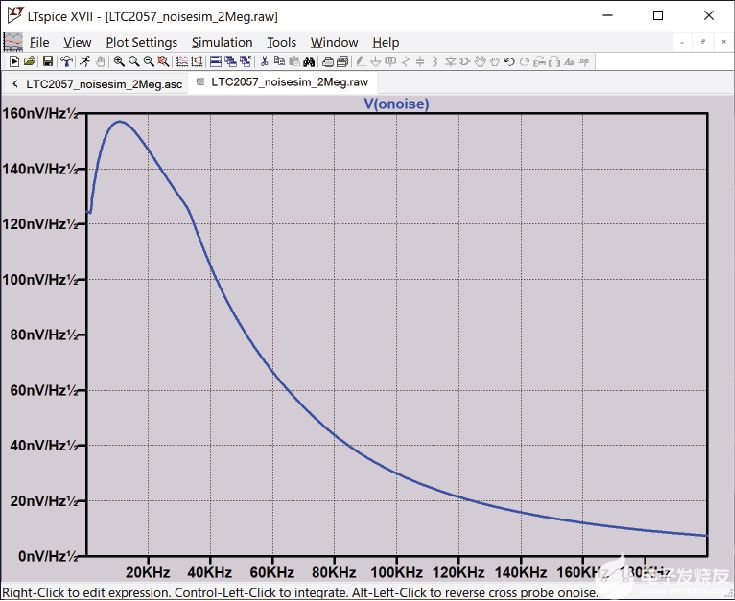
图 23.LTspice 用于在 +10 的同相增益配置中模拟 LTC2057 的输出噪声。LTspice提供了简单的噪声积分工具，但任何仿真的结果都可以导出并导入到Python中以进行进一步分析。

在Python中导入LTspice噪声数据以进行频域分析是设置仿真命令的问题，以便仿真分析矢量中的精确频率。在这种情况下，噪声仿真的最大频率为2.048 MHz，分辨率为62.5 Hz，对应于采样率为4.096 MSPS的第一奈奎斯特区。图 23 显示了 LTC2057 在同相增益 10 下的仿真、仿真输出和导出的数据格式。

为了确定给定噪声频带对信号的影响（信噪比），噪声在目标带宽上进行和方根积分。在LTspice中，可以通过设置绘图限值，然后按住控制单击参数标签来积分绘制的参数。整个2.048 MHz仿真的总噪声为32 μV rms。在 Python 中实现此操作的函数如图 24 所示。

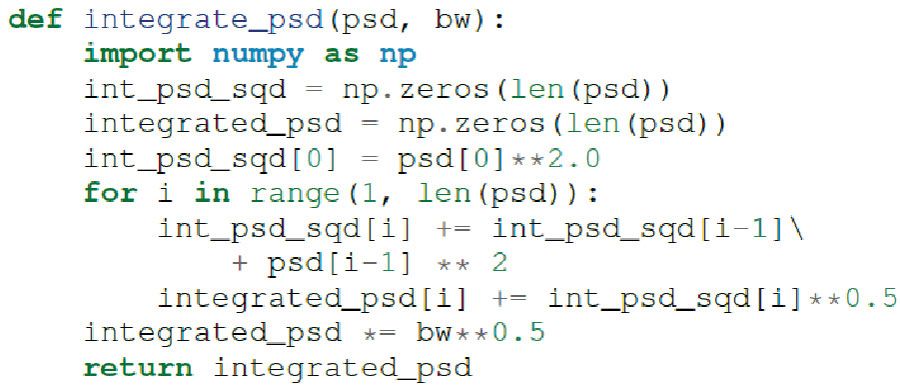
图 24.用于平方根实现的 Python 代码。

读取导出的噪声数据并传递给integrate_psd函数会导致总噪声为3.21951e-05，非常接近LTspice的计算。

产生测试噪声

扩展了纯模拟噪声发生器的功能，它不仅能够产生平坦的噪声分布，而且能够产生任意的噪声曲线，即平坦的噪声带、粉红噪声或模拟某些放大器中的峰值的噪声山脉，这是非常有用的。从图25中的半频谱代码块生成的时间序列从所需的噪声频谱密度（可以手动生成，也可以从LTspice仿真中获取）和时间序列的采样速率开始，然后产生一个电压值的时间序列，可以发送到DAC。

图 25.用于生成任意噪声配置文件的 Python 代码。

此功能可以通过libm2k脚本控制一个ADALM2000，然后使用第二个ADALM2000和Scopy GUI中的频谱分析仪验证噪声曲线。ADALM2000代码片段的推送噪声时间序列（见图26）在ADALM2000 W2输出端产生四个1 mV/√Hz噪声频段（W1上带有正弦波，用于双重检查功能）。

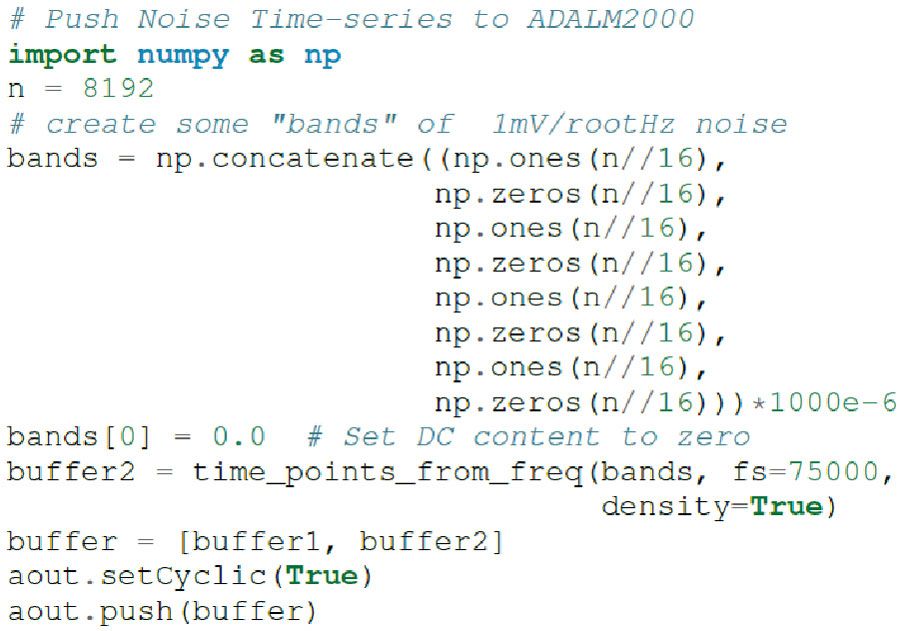
图 26.使用ADALM2000验证任意噪声。

图27显示一个ADALM2000产生的四个1 mV/√Hz噪声频段。输入矢量长度为 8192 点，采样率为 75 kSPS，带宽为每点 9.1 Hz。每个频段为 512 点，或 4687 Hz 宽。~20 kHz以上的滚降是DAC的sinc滚降。如果DAC能够实现更高的采样率，则可以通过插值滤波器对时间序列数据进行上采样和滤波。11

图 27.Scopy频谱分析仪用于验证任意噪声发生器。噪声带之间的深陷波暴露了分析仪的本底噪声，表明可以准确生成任意噪声曲线。

该噪声发生器可与纯模拟发生器结合使用，以验证信号链的抑制特性。

建模和验证ADC噪声带宽

外部噪声源和高于f的杂散音调S/2将折回（别名）到 DC 到 fS/2区域和转换器可能对远高于f 的噪声敏感S/2.以LTC2378-20为例，其采样速率为1 MSPS，–3 dB输入带宽为34 MHz。虽然在如此高的频率下性能可能不是最好的，但该转换器将数字化超过 68 个奈奎斯特噪声区，并将它们折叠回信号顶部。这说明了抗混叠滤波器对宽带ADC的重要性。用于精密应用的转换器通常采用Σ-Δ（如AD7124-8）或过采样SAR架构，其中输入带宽受设计限制

考虑滤波器（包括ADC的内置滤波器）的等效噪声带宽（ENBW）通常很有用。ENBW是平坦通带“砖墙”滤波器的带宽，其允许通过的噪声量与非平坦滤波器相同。一个常见的例子是一阶RC滤波器的ENBW，它是：

其中 fC是滤波器的截止频率。如果将宽带噪声（从“直流到日光”）施加到1 kHz一阶低通滤波器和1.57 kHz砖墙低通滤波器的输入端，则输出端的总噪声功率将相同。

图28中的ENBW示例代码块接受滤波器幅度响应并返回有效噪声带宽。计算单极点滤波器的幅度响应，并用于验证ENBW = fC× π/2 关系。

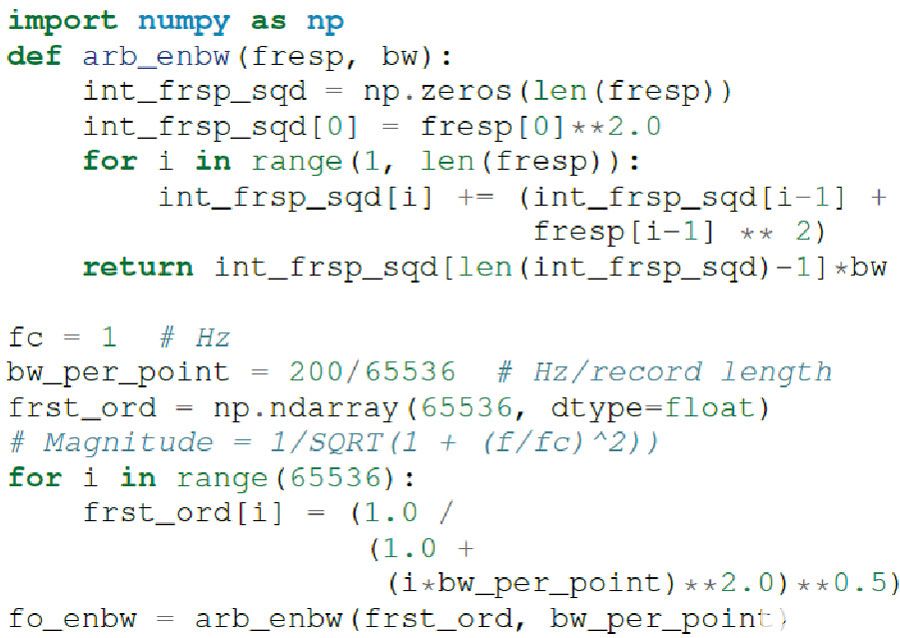
图 28.计算有效噪声带宽的Python代码示例。

该函数可用于计算任意滤波器响应的ENBW，包括AD7124的内部滤波器。AD7124 sinc4滤波器的频率响应，128 SPS采样速率可以通过类似于前面的50 Hz/60 Hz抑制滤波器示例的方法计算。arb_anbw函数返回大约 31 Hz 的 ENBW。

ADALM2000噪声发生器可用于验证此结果。将测试噪声发生器设置为产生1000 μV/√Hz频段，总噪声约为5.69 mV rms，测量结果约为5.1 mV rms总噪声。示波器捕获ADC输入信号显示在ADC输出数据旁边，如图29所示。请注意，测得的峰峰值噪声为426 mV，而ADC峰峰值噪声约为26 mV。虽然如此高的 10 使用Python分析混合模式信号链中噪声的简单方法 噪声水平在实际的精密信号链中（希望）是不现实的，但本练习表明，可以依靠ADC的内部滤波器作为信号链中的主要带宽限制元件，从而降低噪声。

图 29.1 mV/√Hz噪声频段驱动至AD7124-8输入。噪音的定性降低是显而易见的;ADC输入端的峰峰值噪声为426 mV，导致ADC输出端的峰峰值噪声约为25 mV。考虑到ADC滤波器的1 mV/√Hz噪声密度和31 Hz ENBW，5.1 mV rms总输出噪声接近预测的5.69 mV rms。

结论

噪声是任何信号链中的限制因素;一旦噪声污染信号，信息就会丢失。在 构 建 信号 采集 系统 之前， 必须 了解 应用 要求， 进行 相应 的 选择 元件， 并 测试 原型 电路。本教程提供了一系列方法，用于准确建模和测量传感器和信号链噪声，这些方法可在设计和测试过程中使用。

审核编辑：郭婷