本文介绍了射频 (RF) 阻抗匹配的基础知识、如何计算匹配分量以及如何检查LTspice.
介绍
电子理论指出,当源电阻与负载电阻匹配时,最大功率从源端传输到负载。然而,对于大多数RF电路,源阻抗和负载阻抗具有电抗元件,在这种情况下,源阻抗必须等于负载阻抗的复数共轭,以实现最大功率传输。换句话说,虽然源阻抗和负载阻抗的实部必须匹配,但负载阻抗的虚部必须与源阻抗的虚部在符号上相反。
RF功率放大器电路的复杂性很大程度上是由于主要有源元件周围的阻抗匹配元件,无论是晶体管还是集成解决方案。一旦了解了这些RF阻抗匹配电路是如何计算的,电路的其余部分就更直接了。计算这些匹配的组件是一个简单的过程,但有时最好有一个工具来交叉检查这些计算,并确保最大功率确实从电源传输到负载。
本文深入探讨了Chris Bowick的《RF电路设计》一书中概述的阻抗匹配理论,许多工程师将其视为射频圣经。读者可能希望参考本书,以更全面地了解其他RF阻抗匹配网络。整篇文章还包括LTspice仿真,以交叉检查计算结果。
调谐电路和负载Q
电容器的电抗由公式1给出。

将顶部和底部乘以j意味着电容器具有负电抗。相反,电感的正电抗由公式2给出。

因此,如果我们把一个电容器和一个电感器串联起来,它们都有 在一个特定频率下相等但相反的电抗,它们形成一个短的 零相移电路。同样,如果将这些组件并联放置,它们将形成具有零相移的开路:两个的净阻抗 通过将阻抗的乘积除以并联分量来找到并联分量 它们的总和,如果它们具有相等但相反的电抗,则电抗产生 零值分母,因此是开路。
如果电阻器与电抗元件并联或串联放置,则 负载Q描述了电抗与电阻的比值。加载的 Q 并联电路定义为:

串联电路的负载Q定义为:

其中 Rp 和 Rs 是并联和串联电阻,Xp 和 X 是 并联和串联电抗。
我们可以使用网络的加载Q将并行网络转换为串联 网络,从而使匹配变得容易得多。一次系列相当于 导出一个网络,然后只需选择源阻抗即可 相等的实数,但相反的虚部完成阻抗匹配。
图1所示电路的阻抗由下式给出

其中–jXcp是并联电容器的电抗。
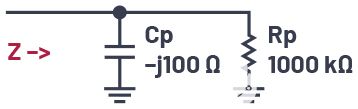
图1.并行 CR 网络。
该电路的串联等效值可以通过多种方式计算。顶部和 公式5的底部可以乘以分母的复共轭,得到实数和虚部级数。或者,该方程可以 转换为极性形式,实数和虚部分量可以是 使用正弦和余弦计算。
获得串联元件的更快方法是找到并行网络的负载Q(Qp)(使用公式3),然后使用公式

以找到新系列电阻。然后,我们设计一个具有相同Q值的串联网络,并将新的串联电阻Rs放入公式4中,以找到新的串联电抗Xs。等式6的推导如附录所示。
因此,图1中的电路元件给出的负载Q值为10,这是通过将并联电阻除以并联电抗得出的。使用公式6,我们可以将并联的1 kΩ电阻转换为9.9 Ω的串联电阻Rs。然后,我们可以使用公式4计算出串联电容需要具有–j99 Ω的电抗。因此,在给定频率下,图1中的电路与图2中的电路具有相同的阻抗。
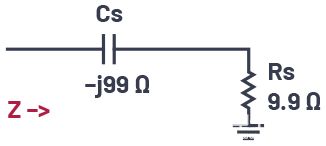
图2.图1所示电路的串联表示。
由于负载的实部为9.9 Ω,负虚部(–j99 Ω),因此我们需要一个实部为9.9 Ω的源阻抗和一个正虚部(+j99 Ω),以确保实现最大的功率传输。实际上,通过选择与负载电抗相等但相反的源电抗,这两个电抗相互抵消(产生短路),我们只剩下源电阻驱动相同的负载电阻。
现在,图2中的串联电路仅相当于图1中的电路。我们不必更改图 1 的配置。如果我们使用串联阻抗为(9.9 + j99)Ω的源驱动该并联电路,则将传输最大功率。
需要注意的是,并联电抗(在本例中为Cp)通过电路Q值确定的系数产生相当于1 kΩ电阻的较低值串联。该电抗可以是串联电容器或串联电感器。反之亦然。在串联RC电路中(如图2所示),串联电抗(无论是容性电抗还是电感电抗)产生串联电阻的更高值并联等效值Rs。实际上,我们可以重新排列公式 6 以读取

这立即向我们表明,并联电阻是(Q2+ 1) 倍于系列等效值。
总结前面的例子,我们可以使用并联或串联电抗使电阻看起来更小或更大。并联RC网络的负载Q值由其电阻与电抗之比决定。我们用这个负载Q将并联网络转换为串联网络,然后选择源阻抗的实部等于(串联)负载阻抗的实部,然后选择源阻抗的无功部分相等但与串联负载阻抗的无功部分相反。
使用固定源阻抗和负载阻抗
不幸的是,我们很少能够改变源阻抗。源阻抗和负载阻抗通常是预先确定的,因此我们必须设计一个匹配两者的网络
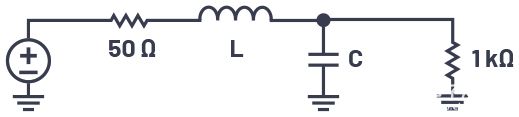
图3.将50 Ω源与1 kΩ负载匹配,频率为100 MHz。
图3显示了一个50 Ω源,需要与100 MHz时的1 kΩ负载匹配。并联电容需要将并联的1 kΩ转换为串联50 Ω电阻,这意味着该RC组合的负载Q值需要为公式6中的4.36。这将为我们提供50 Ω的等效串联电阻加上一定值的串联电容。然后,我们选择一个串联电感器,以产生与串联电容器相等但相反的电抗。这两个电抗抵消,我们只剩下一个50 Ω电阻馈入50 Ω负载。
我们可以使用公式3来计算并联电容的电抗。所以

并联电容应为6.94 pF,在100 MHz时电抗为–j229 Ω。我们现在有一个并行网络。为了将其更改为串联网络,我们将并联和串联网络的Q等同起来。使用公式4,我们可以看到该并联电路转换为Rs = 50 Ω和

所以 Xs = 218 Ω。
因此,6.94 pF电容和1 kΩ负载的并联组合看起来像一个串联的50 Ω电阻和一个串联电容,电抗为–j218 Ω。选择一个串联电感器给出+j218 Ω可确保匹配网络的电抗部分被取消,并且50 Ω源现在提供50 Ω的有效负载电阻。图 4 显示了最终网络。
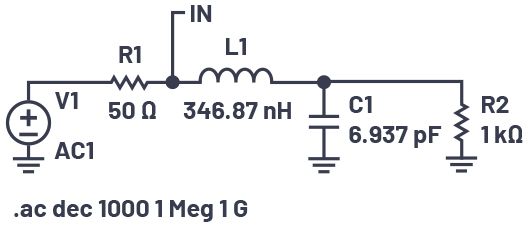
图4.匹配元件,用于将50 Ω源与100 MHz时的1 kΩ负载匹配。
该电路可以在LTspice中仿真。电路结构正常,为方便起见,R1和L1的结点标记为“IN”。源所示,负载阻抗可以通过探测IN节点和流入L1的电流来绘制。在波形窗口中,右键单击 I(L1) 并复制文本。然后右键单击V(in)图标并将文本更改为“V(in)/I(L1)”以绘制匹配网络的输入阻抗,如图5所示。
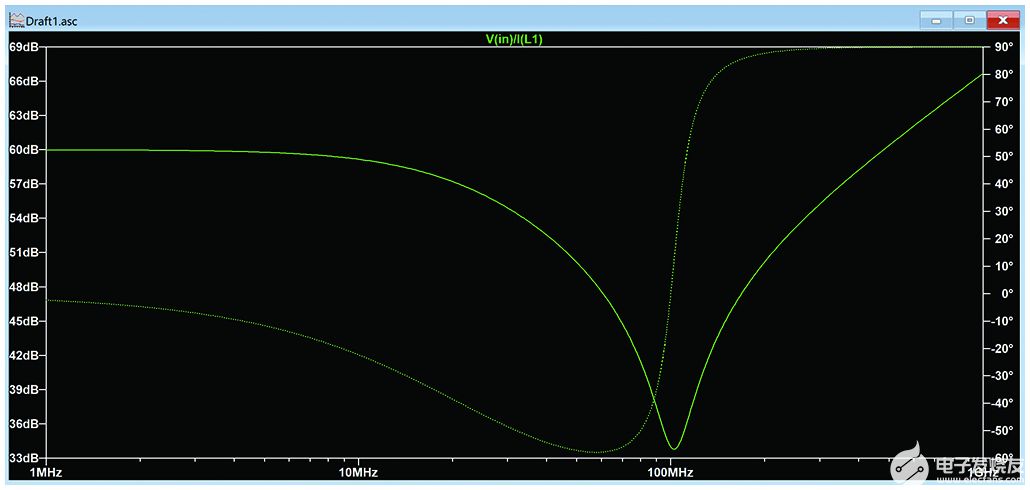
图5.匹配网络的输入图。
但是,图5中的曲线显示了以dB为单位的阻抗。要更改 y 轴以显示实部和虚部,请右键单击左侧的 y 轴,然后将“表示”框从波特更改为笛卡尔,如图 6 所示。
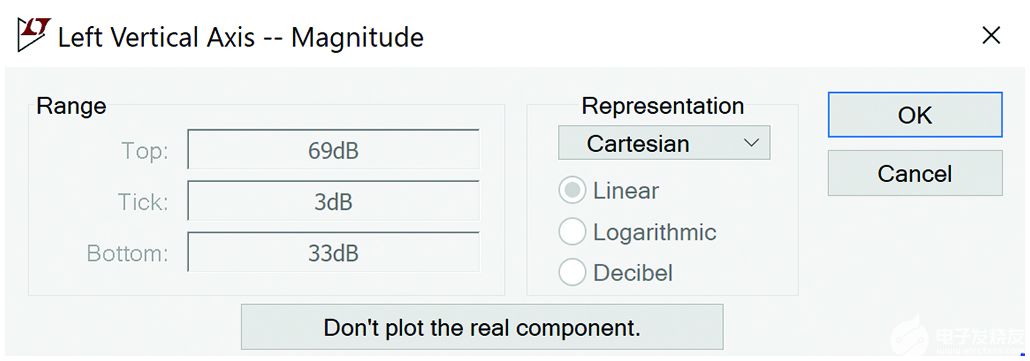
图6.将 y 轴从波特更改为笛卡尔。
最终图如图7所示,实值绘制在左轴上,虚值绘制在右轴上。将光标移动到 100 MHz 位置,我们可以看到匹配网络的输入阻抗确实是 50 Ω,虚部很少。
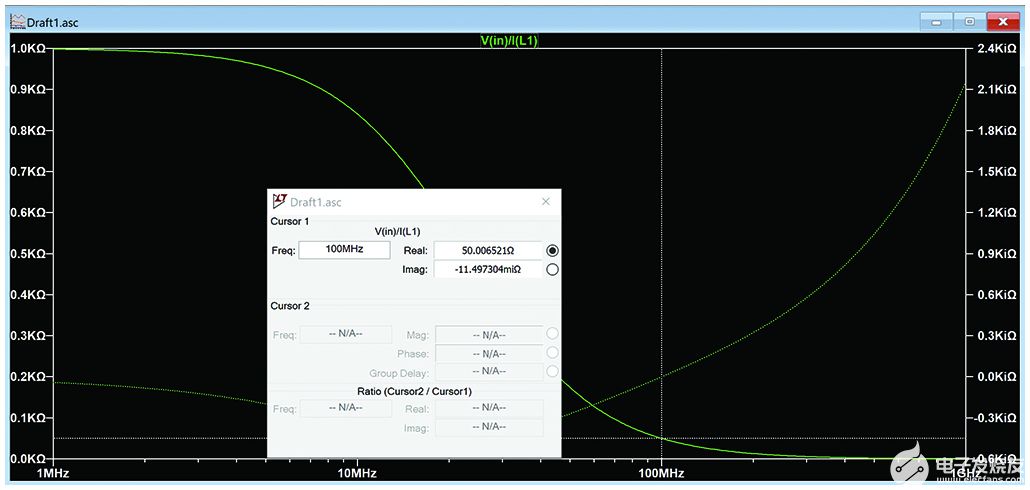
图7.最终图显示了在 100 MHz 下接近 50 + j0 的匹配。
不幸的是,如果我们关闭波形窗口并重新运行仿真,我们需要重新探测V(in)和I(L1),一个除以另一个,然后更改y轴以显示笛卡尔值。通过选择波形窗口并选择“文件>将图设置另存为”,可以避免这种乏味,如图8所示。这将保存当前波形屏幕的设置,并在下一次仿真时自动重新绘制波形。
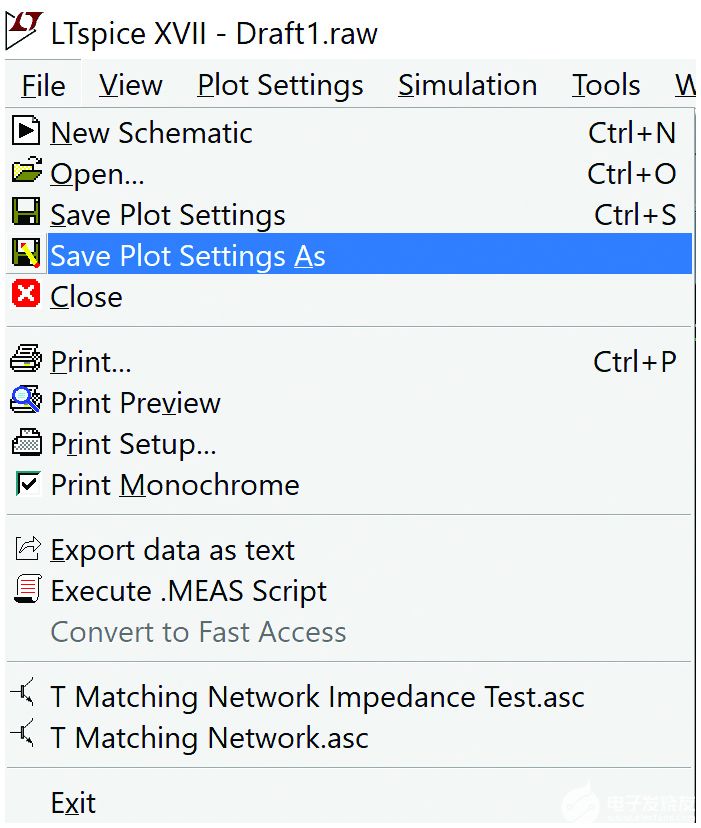
图8.保存绘图设置可保存 y 轴配置和绘制波形。
针对已知 Q 进行设计
在前面的示例中,我们使用并联电容使1 kΩ负载电阻看起来像一个50 Ω串联电阻加上一些任意串联电容,然后选择一个电感来抵消串联电容的电抗。这导致了L网络,如图4所示。遗憾的是,图4中的匹配网络不允许我们选择Q,这是由源阻抗和负载阻抗决定的。克服这个问题的一种方法是使用T网络,如图9所示,它由两个背靠背的L网络组成。
在这个例子中,我们需要使2.1 Ω负载电阻看起来像50 Ω,同时将Q保持在所需的值。为此,我们真正对串联到并行转换技术进行了测试。
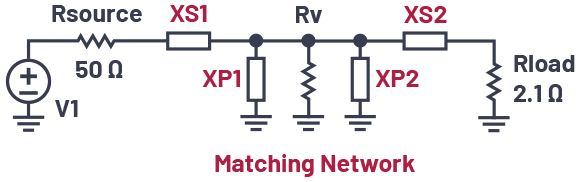
图9.与虚拟电阻器的匹配 T 网络。
在L网络中,我们使用串联电感来抵消串联电容器的电抗(以产生短路)。在T网络中,我们还使用并联电感来抵消并联电容器的电抗(以产生开路)。
查看图9,我们知道串联阻抗XS2(无论是电容器还是电感)将串联2.1 Ω负载电阻转换为更大的等效并联电阻,加上一些任意的并联电抗。因此,我们可以选择XP2与该任意并联电抗相等但相反,并产生开路。然后,我们只剩下2.1 Ω电阻器,看起来像一个更大的并联电阻器,没有电抗元件。
2.1 Ω负载现在看起来像一个大得多的虚拟电阻Rv,如图9所示。请注意,电阻Rv实际上并没有放置在电路中,我们只是使2.1 Ω电阻看起来具有更大的值,从Rv的位置来看。实际上,为了简化电路,我们可以用Rv代替2.1 Ω电阻,XS2和XP2,从源头观察时,电路将在一个特定频率下呈现相同的阻抗。
通过重新排列公式6来读取

我们可以看到,与50 Ω的源电阻相比,该虚拟电阻越大,电路的Q值就越大。因此,我们可以修改XS2和XP2,使Rv看起来像任何值,从而得到我们想要的电路Q。然后,我们可以使用用于L网络的方法将源阻抗(50 Ω)与负载电阻Rv相匹配。然后,我们使用XP1使Rv看起来像一个较小的串联电阻(理想情况下为50 Ω),加上一些任意串联电抗,我们选择XS1相等但与该任意串联电抗相反,因此我们剩下50 Ω源电阻馈入50 Ω负载电阻,但仍保持高Q值。
让我们来看看方法论。我们需要将50 Ω源与100 MHz的2.1 Ω负载相匹配,所需电路Q为10。我们的目标是使图9所示电路看起来像一个L网络,具有50 Ω源和更大值的负载电阻Rv。我们首先需要将2.1 Ω转换为更高值(并联)电阻。我们知道,串联电抗XS2将2.1 Ω转换为更大的并联电阻,因此从公式4

所以 XS2 = 21 Ω。
然后,我们使用公式6将该串联电路转换为其并联等效电路。

所以 Rp 是 212.1 Ω。这是我们的虚拟电阻器。
因此,2.1 Ω的串联电阻和21 Ω的串联电抗看起来像一个更大的212.1 Ω并联电阻加上一些任意的并联电抗。然后,我们插入一个相等但相反的并联电抗来抵消它以产生开路,因此我们只剩下更大的并联电阻。为了确定并联电抗,我们使用公式3,因此

所以 XP2 = 21.21 Ω。
如果需要,我们可以用等于212.1 Ω的单个并联电阻代替XS2、XP2和2.1 Ω电阻,电路将在100 MHz时向源提供相同的阻抗。这可以在LTspice中模拟。该电路现在可以被视为一个简单的L网络,我们只需将50 Ω源电阻与212.1 Ω的负载相匹配。根据公式10,

我们需要使这个并联的212.1 Ω电阻看起来像一个串联的50 Ω电阻。我们知道电阻,我们知道Q,所以我们现在可以计算出实现这个Q所需的并联电抗。插入并联电抗将这个高值并联电阻转换为较低值的串联电阻(50 Ω),加上一些串联电抗。从公式3,

所以 XP1 = 117.8 Ω。
因此,117.8 Ω的并联电抗使并联212.1 Ω电阻看起来像一个50 Ω的串联电阻。然后,我们可以使用公式4来计算串联电抗。
并联电抗为117.8 Ω,电阻为212.1 Ω,Q为1.80。将其转换为具有相同Q值和50 Ω串联电阻的串联电路,使我们能够计算串联电抗。
从公式4,

212.1 Ω的并联电阻和117.8 Ω的电抗看起来像50 Ω的串联电阻加上90 Ω的电抗。如果 X小一是一个电容器,这转化为串联电容(电抗 –J90 Ω),因此串联匹配分量必须是感性的(电抗 +J90 Ω),因此电抗抵消。
从上述过程中有几点需要注意。首先,对于T网络,设计从电路末端使用最低值电阻开始,在上面的例子中,电阻是2.1 Ω,而不是50 Ω。从公式6可以看出,如果我们从50 Ω端开始,我们将计算出更高的Rv值,并且由于负载电阻低得多,为2.1 Ω,最终网络的右半部分具有巨大的Q值。其次,我们注意到串联电抗总是与并联电抗相反的符号,因为我们需要确保它们相互抵消。因此,串联电容器通常需要并联电感器,反之亦然。
组件值如表1所示。
| 元件 | 阻抗 | 100 MHz 时的组件值 |
| XS1 | 90 | 17.68 点频 |
| 是的 | 117.8 | 187.5 千兆安时 |
| XS2 | 21 | 75.79 点频 |
| XP2 | 21.21 | 33.76 千兆安时 |
由于XP1和XP2是并联电感,因此可以组合成一个电感器 电感器,值为 28.61 nH。最终电路如图10所示。
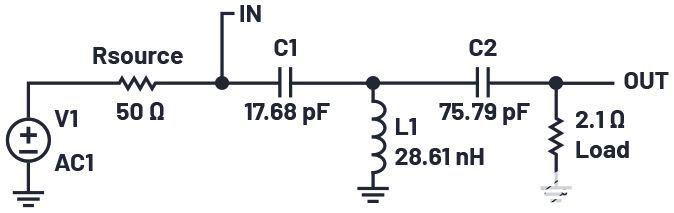
图 10.完整的 T 网络。
绘制IN节点的电压并将其除以流入C1的电流,我们可以看到匹配网络的输入阻抗非常接近50 Ω,如图11所示。
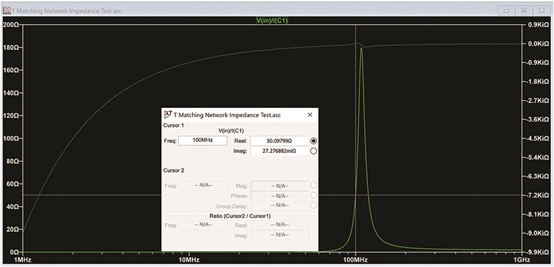
图 11.100 MHz 时的输入阻抗图。
我们还可以通过绘制负载两端的电压和流过负载的电流并逐一相乘来绘制传输到负载的功率,如图12所示。
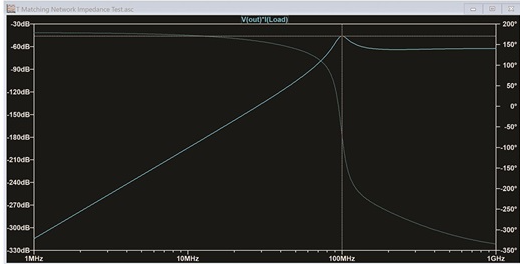
图 12.最大功率以 100 MHz 传输。
通过右键单击绘图窗口并选择添加绘图窗格,我们可以在一个窗口中同时绘制匹配,在另一个窗口中绘制功率传输。保存绘图设置可确保在每次仿真后自动绘制这些设置。
处理复杂负载
负载很少是纯电阻性的。如果图10中的2.1 Ω负载具有398 pF的串联电容元件(在100 MHz时等于–j4.0 Ω),则会破坏匹配网络。但是,这很容易克服。在图10中,C2和2.1 Ω负载形成一个串联网络,其Q值为10,由电抗(–j21 Ω)与电阻(2.1 Ω)之比决定。额外的–j4.0 Ω将总电抗增加到–j25 Ω。为了保持相同的Q值,我们需要在该串联组合中增加一个正电抗,以消除负载的–j4.0 Ω。这可以通过在与C2串联时增加6.37 nH的电感(电抗为+j4.0 Ω)来实现,以保持电抗与电阻的比值。更方便的方法是将电容C2的值增加到93.62 pF。这会将电抗降低到–j17 Ω,然后负载电容将净串联电抗增加回–j21 Ω,从而保持Q为10。LTspice可用于提供健全性检查,最终电路如图13所示。
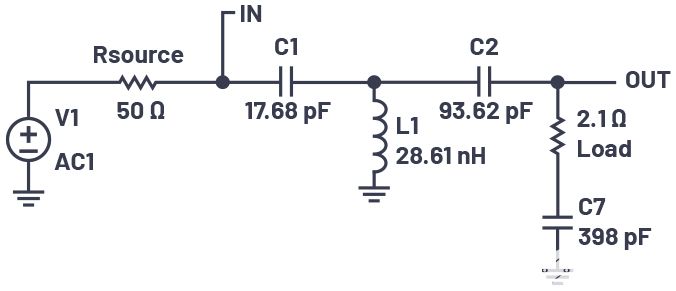
图 13.与复杂负载匹配的修订后的 T 网络。
图14显示,该电路在100 MHz时与50 Ω具有良好的匹配,并传输最大功率。
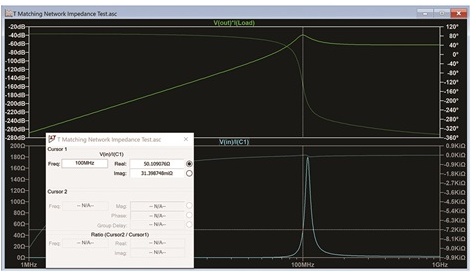
图 14.100 MHz 复数负载下的功率输出和输入阻抗图。
结论
希望本文揭开了RF阻抗匹配的神秘面纱,并使RF功率放大器电路更易于理解。使用网络的负载Q值,我们可以在串联和并联网络之间切换,并将低值电阻转换为高值电阻。然而,与任何工程任务一样,对计算进行交叉检查总是好的,LTspice在绘制电路的输入阻抗和功率输出方面证明是无价的。
审核编辑:郭婷
-
电容器
+关注
关注
64文章
6222浏览量
99637 -
射频
+关注
关注
104文章
5585浏览量
167753 -
电感器
+关注
关注
20文章
2330浏览量
70536
发布评论请先 登录
相关推荐
阻抗匹配设计的实现
基于Ansoft Designer的射频功放电路阻抗匹配优化
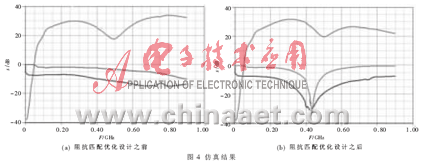
怎样理解阻抗匹配_pcb阻抗匹配如何计算

阻抗匹配的原理及应用
射频(RF)阻抗匹配:计算和仿真





 射频阻抗匹配:计算和仿真
射频阻抗匹配:计算和仿真










评论