题图为SGM算法的一个处理结果。
最近来看看一些双目稠密匹配的算法。说来惭愧,SGM在航测领域是很重要的算法(当然也是最好的双目稠密匹配算法之一),自己却没有认真读过,只是大致有些了解。
看了论文,再结合网上一些资料,自己做了些论文笔记。
想到关于SGM论文网上还没看到比较翔实的博客,就把自己做的笔记再加些解释分享出来了(下文中的引用部分多为我自己的思考)。
其中还有一些是自己不理解的地方,准备后续写代码时研究。
也希望大家可以分享自己的见解,或对文章内容进行批评指正。
由于是论文笔记,所以有些中英夹杂,而且有些想想也不好翻译,就不再改了。闲话少说,直接来看论文吧。
基础
双目图像稠密匹配的4个基本步骤为:
Matching cost computation;
Cost aggregation: connects the matching cost within a certain neighborhood;
Disparity computation: selects the disparity with the lowest matching cost;
Disparity refinement: removing peaks,
interpolating gaps or increasing the accuracy by sub-pixel interpolation.
这4个都比较好理解,SGM论文也是按照这样来组织的。
下面就按照论文的顺序来详细了解下SGM算法。
中心思想及要求
idea: 使用MI (Mutual Information) 来进行单像素匹配 + 多个一维平滑约束(来拟二维约束)来进行“全局”优化。
前提: 已知立体像对间的对极几何关系。

Pixelwise cost calculation
SGM算法不用图像块进行匹配,只考虑当前像素。因为利用图像块进行匹配对应的隐性约束为块内像素的视差是相同的,而这在深度变化(物体边界)的地方是不成立的。
互信息(MI):defined from the entropy(熵)of two images:
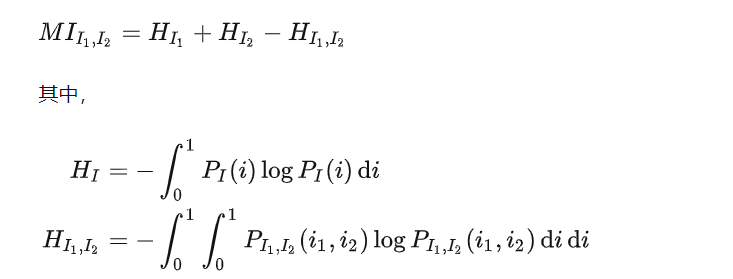

上式针对整张图像而非单个像素,不能用作 cost。因此,对于一张图像的联合熵,有其他论文利用泰勒展开计算:
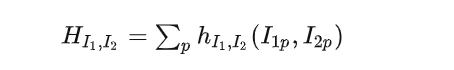
其中,公式内第一项为像素 p 的灰度值,第二项为匹配像素的灰度值。
这里,联合熵被简化为左图所有像素点(及其对应点)的 h(i1,i2) 之和。
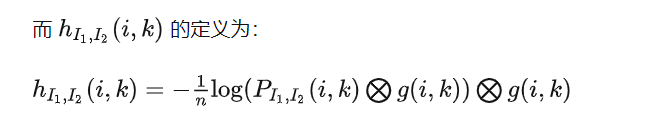


可以看到,由于极线矫正后左右图十分相似,所以得到的联合分布直方图类似于一个对角矩阵。
以上计算并不包含被遮挡的像素(如何得知哪些像素是被遮挡的?)。因此,为了避免包含遮挡像素,建议将熵也这么计算:
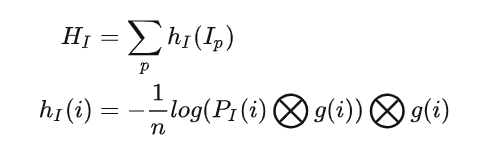
此外,以上计算也只针对两张图像的重叠部分。
因此,一维直方图也可以这么计算:
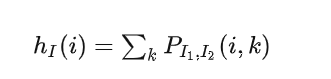
h(i) 即为 P(I1, I2) 第 i 行(列)像素之和。
最终,互信息的定义为
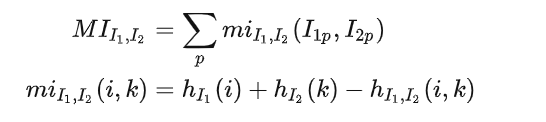

对于像素点 p,若取其视差为 d,则对应的 cost 为:
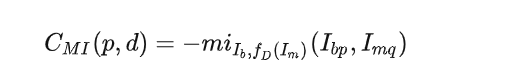
问题:想要对匹配图像 Im 进行视差矫正就需要视差图。
但我们的目标就是获取视差图。
解决:
迭代法:start with a random disparity map for calculating Cmi. And use the cost for matching and calculating a new disparity map.
论文表示大致迭代3次就可以了。
层次法:recursively use the up-scaled disparity map (half resolution). Start with a random disparity map of 1/16 resolution. 在这个1/16的视差图上重复计算3次(每次迭代3次,然后每放大一倍迭代3次计算出新的视差图。

Aggregation of costs
以上就是论文进行匹配的第一步。接下来就要进行一个“全局”上的优化。
pixelwise matching 还是不够稳定,因此需要加上一些约束来保持同一平面的像素具有相同的视差并惩罚邻域内视差不连续的像素(即平滑)。
所以最小化如下能量方程:
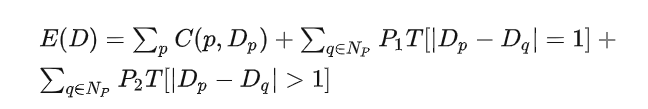
上式第一项为所有 MI cost 的和;
第二项对 像素p的邻域内出现视差与p的视差相差1 的像素 加上一个惩罚项P1;
第二项对 视差相差大于1 的像素加入更大的惩罚P2.

作用:对于小的视差相差使用较小的惩罚以适应斜面或曲面;
对大的视差相差使用大的惩罚来防止深度(视差)不连续。
问题在于全局最小化 E(D) 是一个 NP 完全问题,很难解算。
单行(1D)约束可以利用动态规划达到多项式时间。
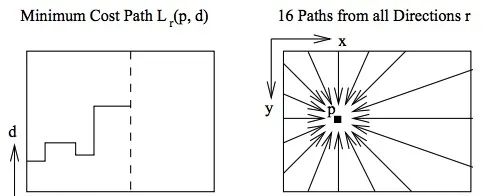
因此很自然地想到优化多个单行的约束条件来拟合2D优化,作者建议至少要选择待优化像素的8个方向。
The aggregated smoothed cost S(p, d) for a pixel p and disparity d is calculated by summing the costs of all 1D minimum cost paths that end in pixel p at disparity d.(也就是说S是所有L之和。)
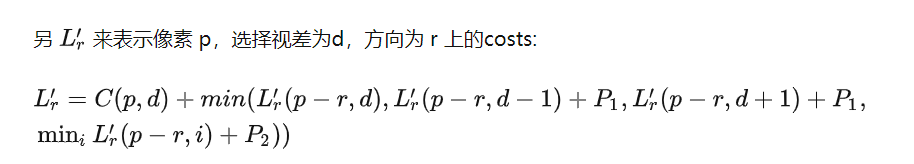

考虑到上述代价最后可能非常大,可将之修改为:
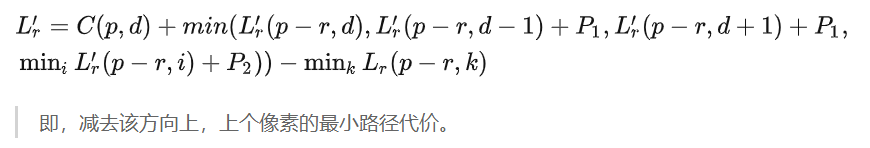
注意到被减项对于该方向上,像素 p 的任意视差都是一个常数(上一个像素的视差及其对应的最小cost已经计算好)。
最终,对于像素 p,选择视差 d 的cost 就是:
S(p,d)=∑rLr(p,d)
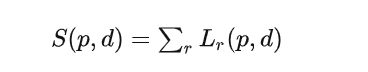
选择使 S(p, d) 最小的视差d. 若要到亚像素精度,可以利用 neighboring costs 来拟合一个二次曲线。

Multi-baseline matching
对左图计算完视差图后,还可以以同样的方法来对右图进行视差图的计算,在将二者融合起来。也可以利用多个立体像对来计算多张稠密视差图。
问题:areas which are not seen by all images will become invalid.
解决:取多视差图的并集而非交集。
对于左图来说,它的视差图是恒定值(参考依据视差计算深度的公式),因此可以通过多图匹配来优化。
对左图计算一个视差图后,也可对右图计算一个视差图。然后进行一致性校验:
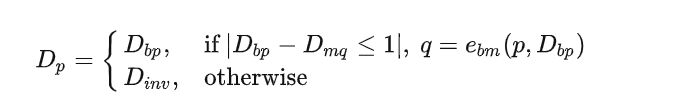
如此,确保 one to one mapping (uniqueness constrain).
Disparity Refinement
之后,是对所得的视差图进行优化处理。个人觉得这是双目稠密匹配很重要的一步,因为对于很多算法,其得到的视差图之间的差别并不会特别大。
重要的是对所得的视差图进行后处理,提高深度计算的精度。
移除极值
采用联通域分割法,将视差相差在1个像素以内的像素4邻域归为一个联通域来分割所得的视差图。
根据场景事先确定一个大小阈值,去除像素数量过少的联通域。
Intensity Consistent Disparity Check
这步是SGM后处理比较核心的一步。
室内场景的前后景之间会有视差不连续。
但前述的能量方程对于发生视差不连续的位置没有偏好,这种不连续可能在错误的地方出现,因此会造成错误的前后景物体边界,或者一个斜面。
先前的将像素梯度与惩罚值P2关联可以部分解决该问题。
但在一些视差不连续的不对称的情况(如前景物体没有完全出现,只在出现的一边产生视差不连续)下可能失败(原因待解)。
室内环境中,后景常常为无纹理区域,如墙等。为解决这个问题,先提出以下三个假设:
无纹理区域内部没有视差不连续现象(即视差变化伴会随梯度变化);
无纹理区域包含一些弱纹理(否则也无法进行像素匹配);
无纹理区域的表面可以用一个平面表示(参考1,如此则区域内视差恒定。否则为两个可以分割开的区域)。
解决步骤:先对图像进行分割,得到前后景区域。问题就变为如何正确选择后景(无纹理区域)的边界和视差,较好的分割出前景物体。
利用 fixed bandwidth Mean Shift Segmentation 方法分割原始图像,得到各个无纹理区域(假设1),忽略过小区域,所得区域表示为 Si。
利用联通域分割法分割步骤1得到的无纹理区域(假设2),忽略过小区域,所得分割区域表示为 Sik;
针对2得到的区域拟合平面 Fik (假设3)。将得到的各个可能平面推广到所在的整个无纹理区域,取能量方程最小的平面。
遮挡判断子步骤:对于像素p,若其匹配像素q有了另一个匹配,且新的匹配像素的视差大于像素p,则像素p认为被遮挡;
该无纹理区域内的视差都替换为最佳拟合平面所对应的视差;
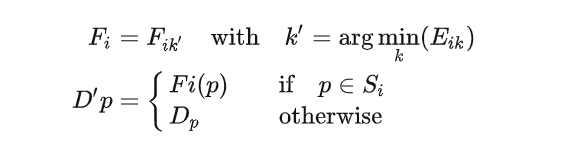

Discontinuity Preserving Interpolating
后处理完的视差图可能因为遮挡或误匹配而存在缺失区域。对这些区域的视差进行插值前要对其性质进行分类,以使用不同的插值方法:
遮挡:用背景的视差进行外插值,而不使用前面的遮挡物的视差;
误匹配:可以利用其周围像素进行内插值。
注意:对与遮挡相连的误匹配区域,同样利用背景像素进行外插值。
区分:由于遮挡会照成视差不连续。被遮挡位置的像素的极线不与disparity function(即视差随位置变化的方程)相交;误匹配像素则相反。
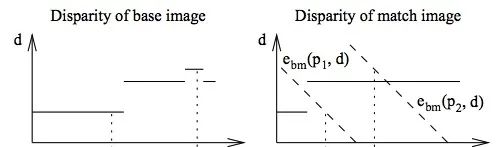
如上图,点p1处就是因为遮挡而造成点缺失;而点p2则是因为误匹配。
插值仍然是从像素周围的8个方向计算出8个可能的视差值,然后
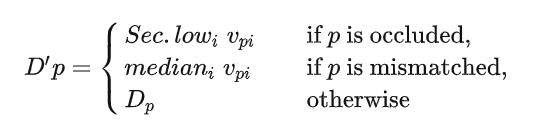
该式的第一项是选择待选视差中第二小 (second lowest) 的视差。第二项为选择待选视差的中值,这样有利于在物体边界处保持视差不连续。
该插值方法独立于立体相对匹配算法。
最后可以再用中值滤波对得到的视差图进行去噪处理。
最后,作者还介绍了对于超大幅的航空影像进行分块处理的方法和加速技巧.
以及解释了文章中不先对右影像整张影像进行极线矫正的原因(对于推扫式的航空/航天影像,其极线为曲线,因此无法进行矫正,只能实时计算)。
但对于其他普通立体像对,这些内容都是不必要的,就不再解释了。
审核编辑:汤梓红
-
算法
+关注
关注
23文章
4637浏览量
93529 -
SGM
+关注
关注
0文章
5浏览量
10611 -
匹配算法
+关注
关注
0文章
24浏览量
9394
原文标题:一文读懂经典双目稠密匹配算法SGM
文章出处:【微信号:vision263com,微信公众号:新机器视觉】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
双目立体视觉三大算法原理及其代码实现
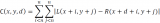
双目立体视觉原理大揭秘(一)
【Firefly RK3399试用申请】基于双目摄像头的视觉景深算法开发
双目视觉立体匹配算法研究
双目立体计算机视觉的立体匹配研究综述

一种基于PatchMatch的半全局双目立体匹配算法





 一文读懂经典双目稠密匹配算法SGM
一文读懂经典双目稠密匹配算法SGM













评论