卡扣连接器应用于电机外壳连接键的设计中

卡扣连接器(也称为紧固件或机构)用于将一个部件直接连接到另一个部件，在空间受限的环境中，它们通常用于组装复杂的注塑成型零件。这种连接结构由于连接方便、加工容易、成本低，被广泛应用于电机外壳连接键的设计中。

众所周知，受挤压机构的弯曲特性会严重影响电机的性能。在研究这些特性时，直接使用目标样机进行验证是很耗费资源的，可能会对样机造成损坏并浪费大量资金。但是，随着计算机技术的发展，这些问题都可以通过 CAE 模拟的方法来解决[1]。有很多关于卡扣的设计研究，但是大部分的研究仍是针对传统卡扣，并且多数集中在塑料卡扣的设计中。一些研究表明，传统卡扣设计的工作原理独立于制造过程，并提出了增材制造卡扣设计指南，很多先前的方法需要适应新制造技术的制造方式[2-3]。

强度、约束、兼容性和稳健性已被确定为卡扣设计的关键要求，前三个在设计阶段是必不可少的。通过遵循一般设计指南，可以较容易地满足这些要求。稳定性高是指尺寸变化的容忍度。坚固性是不可预测的，尺寸会根据制造和材料特性的差异而变化。当我们模拟模型时，假设材料是各向同性的，但材料很难完全各向同性。最关键的尺寸变化是刀具和粘合面之间的匹配角度。过盈量决定了配合力和预紧力的质量。由于卡扣连接器的行为类似于悬臂，因此配合力会随着干扰的增加而增加。过少的干涉会导致装配松动，过多的干涉会导致组装困难或可能导致零件和连接器的永久变形，从而导致废品率高而影响效益。

与恒力机构一样，卡扣连接器是一种封闭结构，当受到一定的输入位移时，它会提供一定范围的恒定反作用力。本研究的卡扣连接器是用于连接电机金属部件，卡扣连接器的质量可以很大程度影响电机的生产以及质量。

大多数的研究主要集中在塑料材料上，很少有关于电机外壳金属卡扣的研究。本文研究了刀具的形状如何影响卡扣材料的变形，评估卡扣压型的整个过程以获得刀具的反作用力，从而调整模具进行冲压成型。

1 材料特性及典型的封装结构

1.1 材料特性

对于塑性材料，其变形过程有四个阶段：弹性阶段(O-a)、屈服阶段(a-d)、应变硬化阶段(d-e)和颈缩阶段(e-f)，分别表示在图 1 中[14]。从O到a的阶段定义为载荷随应变线性增加，当载荷达到某个最大值a后，屈服阶段开始，应力增加很小，但应变增加很大。经过b后，应力减小，应变增大，直至稳定阶段，在应变增大过程中应力保持相对稳定，略有波动。试样一部分的直径开始减小，这种现象称为颈缩(e-f)。颈缩开始后，稍低的载荷足以使试样进一步伸长，直到它最终破裂。这意味着无论负载是否存在，材料都会发生永久变形。

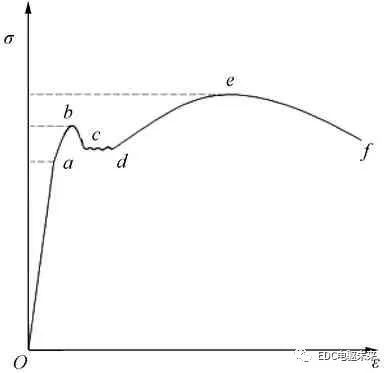
图1 材料的拉伸曲线

为预测不同尺寸结构的性能，采用有限元分析方法评估性能。本文使用ANSYS Workbench 用于压缩模拟，而有些论文使用 Abaqus 进行压缩模拟，虽然软件不同，但都是基于有限元方法对模型进行离散化分析[15-17]。材料的力学性能如表1所示。多线性各向同性硬化参数如表2所示，本文使用表2数据进行分析。

表1 材料力学性能

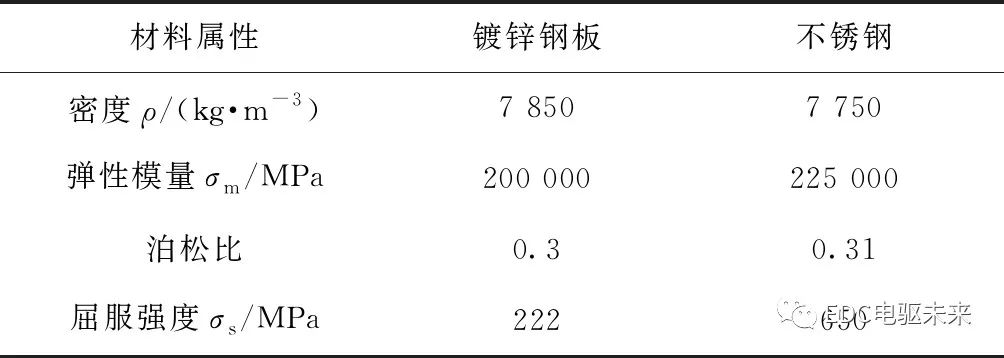
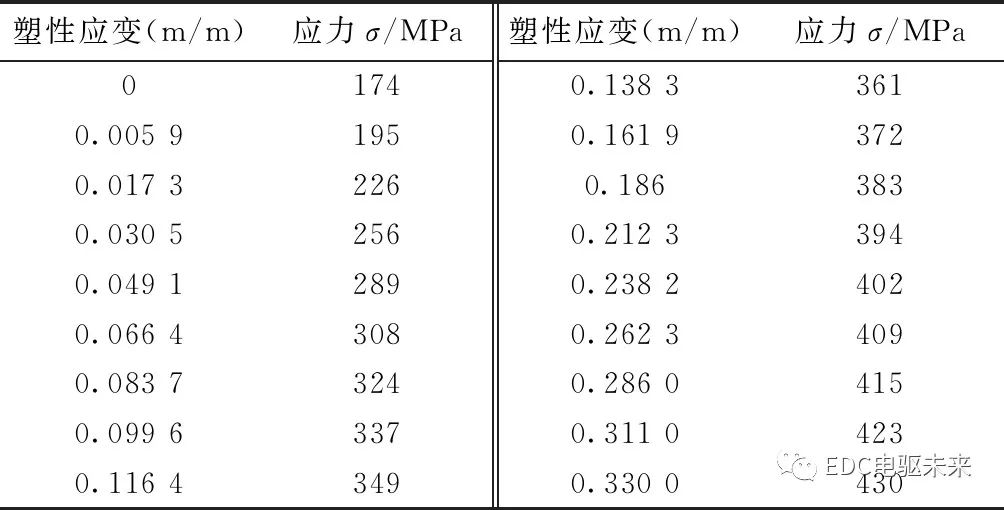
表2 镀锌钢板多线性各向同性硬化模型

1.2 典型的封装结构

图 2 显示了典型的电机卡扣结构。四位槽对称分布在一个空心圆柱体上，相邻槽之间间隔90°。R1和R2分别是内半径和外半径，H1和h1分别是圆柱和孔的高度，b1是刀具的宽度。L1为凹槽宽度，L2为最大夹钳宽度，L3为刀具宽度，L4为夹钳高度，L5为最大凹槽宽度。α是内刀角，β是外刀角。四个孔对称分布在一个空心圆柱体上，相邻两个孔之间的间距为110°。

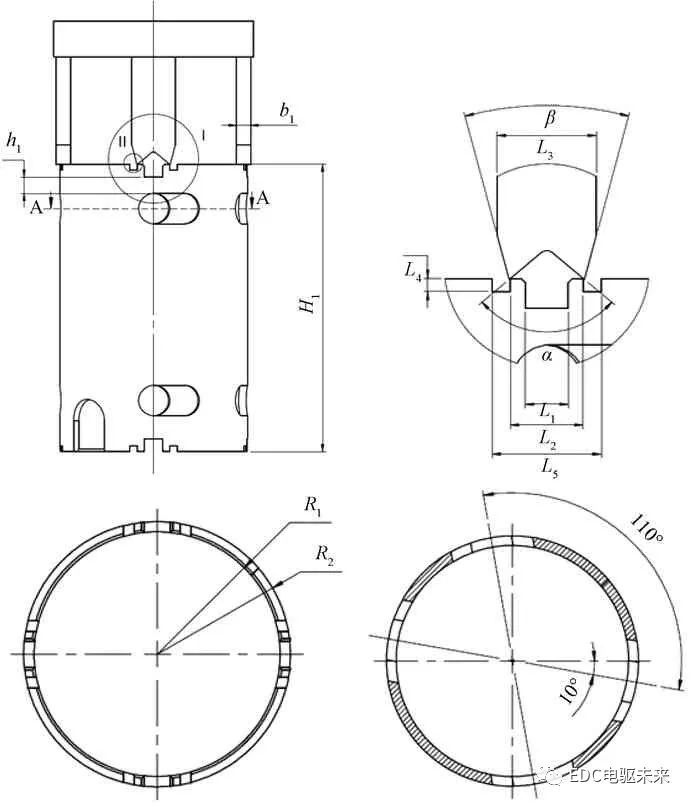
图2 电机外壳结构示意图

在刀具压缩卡扣结构过程中，压缩位移S可以表示：

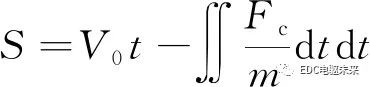
(1)

式中:V0是压缩开始时压缩工具的速度；Fc是压缩过程中的压缩力；m是工具的质量；t是压缩时间。根据图1的材料特性，初始阶段不可避免地存在一个载荷阶段a-c，其中受力大于稳定阶段。本研究认为，当稳定阶段的持续时间占压缩持续时间的 70% 以上时，阶段(a-c)可以忽略不计[18]。在这个假设下，压缩力被认为是恒定的，并且接近于稳定阶段的平均力。然后，假设压缩结束时，速度下降到0，式(1)可简化：

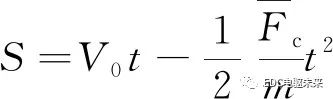
(2)

式中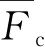：是压缩过程中的平均力；S是总位移；t是压缩过程的整个时间。通过推导可以得出，在压缩过程中，可以按照位移约束的方式进行载荷加载在ANSYS软件中。

1.3 刀具角度的不同参数

刀具的稳定位移是在压缩过程中表现出来的。在压缩过程中，变形主要发生在卡扣锁紧部分处，如图 3 所示。

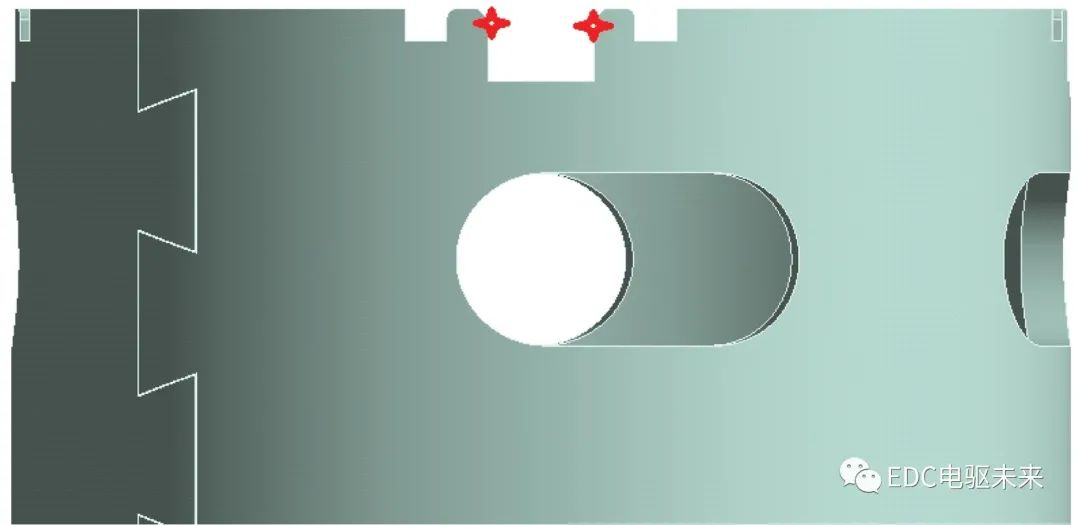
图3 卡扣锁紧部分凸起筋条

压缩过程中铁壳的变形主要受刀具角度的影响。刀具角度α会影响图3中锁紧部分的变形，影响电机外壳的预紧力。本研究确定了锁紧部分和刀具的尺寸。本研究介绍了95°、100°、105°这三个不同的角度来寻找最合适的α角度，压缩过程中的最大压缩为1 mm，确保刀具能够刚好碰到L4的底部并且不会破坏电机外壳。整个过程耗时为 1 s，包含20 个子步。

枚举法通过枚举问题的所有可能答案，找到满足给定条件的合理解。它通常计算量大、效率低，但是，当用于小规模问题时，它无需复杂的计算和推导就能更快地达到解。本研究引入ANSYS Workbench 2021R1，比较不同刀具角度的性能。在 Mechanical Workbench 中，通过 User Defined Result 获取变形后的节点坐标：LOC_DEFX、LOC_DEFY、LOC_DEFZ。通过坐标计算，得到空间中两个端点(图3中红色星状标识)的距离。

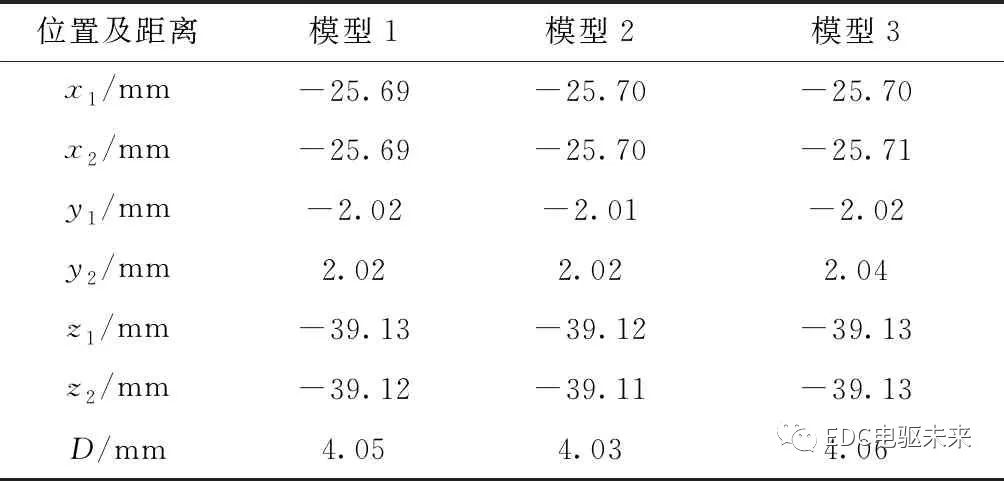
刀具角度列于表3，唯一不同的是角度α，三个仿真模型的其他参数均相同。L1取值为5.2 mm，卡扣锁紧部位的宽度为2 mm。使用式(3)计算表4中的数据，得到卡扣锁紧后两个端点的空间距离，从而对比差异。

两个节点的空间距离公式：

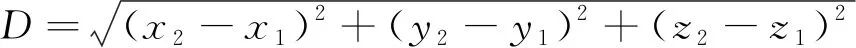
(3)

通过对比如表4所示的结果，可以得到在刀具作用的过程中，卡扣向内变形，锁紧端盖，α=100°时变形后距离最小，变形效果最好。

表3 不同的刀具角度的模型参数

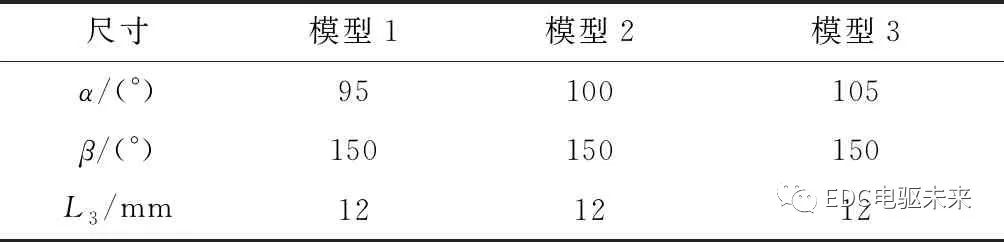
表4 不同刀具角度对应的变形值

1.4 网格无关性验证

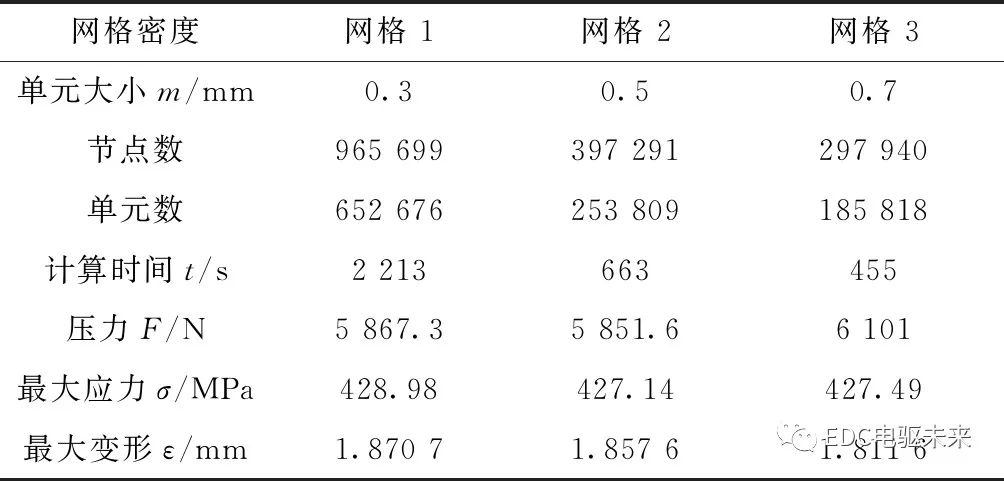
过多的网格会导致计算量的增加，过少的网格也会导致计算精度的降低，本文对电机模型进行网格无关性验证，以保证在满足精度的前提下尽量缩小计算量。测试在DELL 工作站Precision 5820 Tower上测试，处理器Intel(R) Xeon(R) W-2275 CPU @ 3.30 GHz并带有256 GB内存，测试软件平台为Windows 10 专业工作站版，版本号20H2，测试仿真软件平台为ANSYS Workbench 2021R1 带有8核HPC, 最大算力可以调用12个CPU物理内核，所有软件皆在正版授权软件中进行测试。测试模型的刀具角度为95°，分别进行三种单元密度网格无关性验证[19-22]，网格划分方法为全局网格，采用1.5 mm网格尺寸，在卡扣部分采用局部加密方式进行加密，加密网格尺寸及验证结果如表5所示。根据表5所示的数据，选择网格尺寸为0.5 mm时的单元尺寸进行计算。

表5 网格无关性验证

1.5 边界条件

为了获得整个压缩过程中壳体的变形情况，首先通过建模将刀具与电机壳体位置对应，刀具内侧与壳体卡扣凸起部分相接触，由于有润滑的存在，所以刀具与壳体部分的接触设置为无摩擦接触。在实际加工过程中，壳体固定在操作台上，将壳体下表面进行约束处理，约束6个方向自由度。刀具在下压过程中，电机端盖是盖在电机壳体上的，并且没有添加其他约束，端盖只与电机卡扣凹槽部分进行接触，在电机壳体周向移动，径向无法移动，设置好的边界条件如图4所示。端盖释放Z方向的自由度，约束X、Y两个方向的平动自由度，刀具运动方向如图5所示。

图4 电机壳体端盖约束

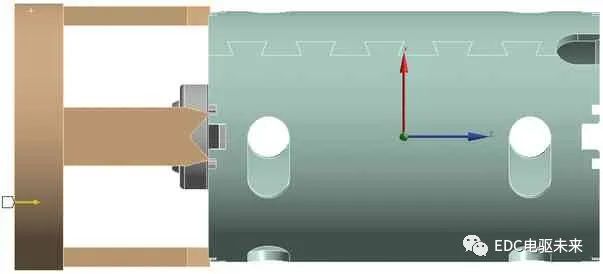
图5 刀具运动方向

1.6 不同刀具角度导致的壳体变形情况

刀具在下压过程中共耗时1 s，分20个载荷步进行施加，在进行锁紧工艺时，整体应力开始变大，材料产生塑性变形，图6～图14列出了100°刀具角度情况下壳体的塑性变形情况。本文的分析在满足壳体平面度要求以及总体变形要求的情况下，尽可能地锁紧端盖，以免端盖出现松动。通过仿真分析可以直观地看出，卡扣卡口部分已经有明显的变形，但是变形只在卡扣锁紧部位，并未传递到电机壳体的其他部位，这正是加工生产所要的效果，符合预期的设计。这样既可以保证卡扣卡位的精准锁紧，又不会影响电机壳体的其他部位的变形，从而影响电机的性能。

图6 100°刀具加工壳体变形情况

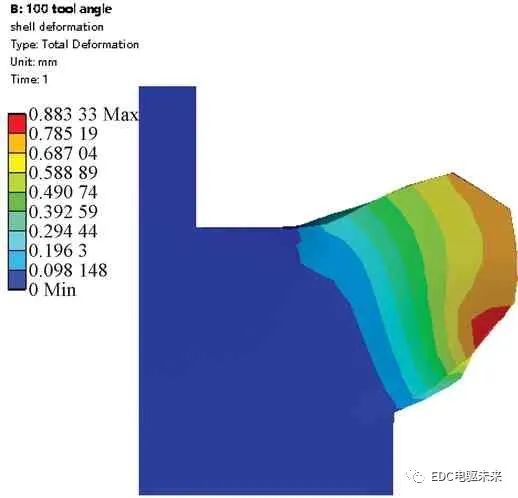
图7 100°刀具加工壳体局部变形情况

图8 100°刀具加工壳体端盖变形情况

图9 95°刀具加工壳体变形情况

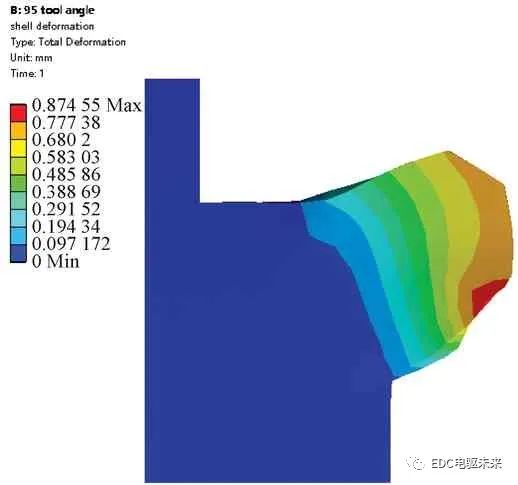
图10 95°刀具加工壳体局部变形情况

图11 95°刀具加工壳体端盖变形情况

图12 105°刀具加工壳体变形情况

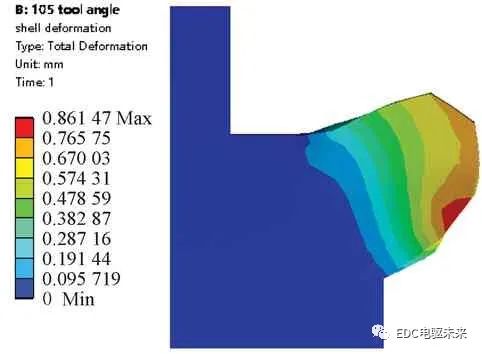
图13 105°刀具加工壳体局部变形情况

图14 105°刀具加工壳体端盖变形情况

1.7 不同刀具角度压缩卡扣结构的压力

通过软件计算，可以得到刀具在下压卡扣的过程中需要多大的下压力，才可以将卡扣锁紧，用于指导实际加工生产中，相关工艺的下压力完成装配。本文对刀具的三个角度的模型进行分析，并得出下压力的精确值，如表6所示。不同刀具角度的下压力是不同的，当刀具角度为105°时，下压力最大。较大的下压力并不是生产中最理想的状态，有可能导致壳体的其他部位变形。而较小的下压力会有压不到位的风险。100°的刀具角度是三种刀具中最优的。

表6 不同刀具角度的下压力

1.8 锁紧结构尺寸的影响

图2中，L1的尺寸与端盖配合，无法进行更改；L2的尺寸为加工后的凹槽，可以通过更改L2的尺寸来调整锁紧结构的变形，从而影响锁紧的效果。同时，调整L2的尺寸，也会影响刀具的压力，较大的压力会对整个结构的变形产生不稳定的作用，压力要尽可能控制在一个合理的范围内。在刀具角度为100°的情况下，L2的初始尺寸为9.2 mm，此时，L1的尺寸为5.2 mm，单个锁紧结构的宽度T为2 mm，宽度的计算公式如下：

T=(L2-L1)/2

(4)

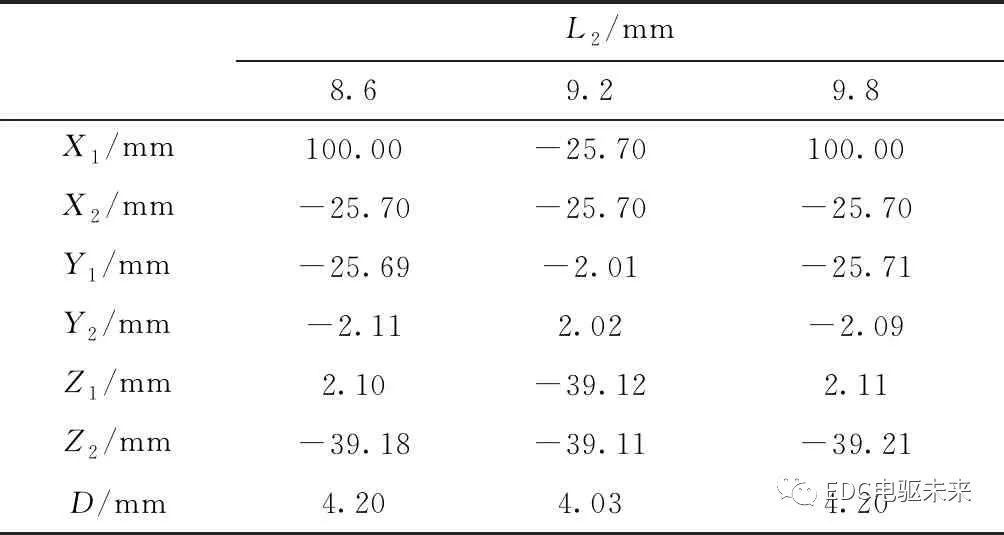
不同的锁紧宽度对压力的影响如表7所示。通过整理表8数据，并根据式(4)计算得到在三种宽度分别为1.7 mm，2 mm，2.3 mm的情况下，相同的刀具角度，不同的宽度值T，卡扣锁紧部位表现的性质不同，当宽度为2 mm时，锁紧效果最好。

表7 不同的宽度对压力的影响

表8 刀具角度100°对应的变形值

2 实验验证

根据仿真结果，确定刀具角度为100°，L2为9.2 mm时的壳体在所有模型中是最优的，此时卡扣锁紧部分的宽度T为2 mm。下面对此参数下的模型制作样机，来验证仿真的精确性。

实验通过两个测试来确定仿真方案是否可行，首先是压力测试，而后是端盖的平面度测试。

2.1 刀具锁紧卡扣实验

卡扣锁紧实验主要进行压力的评估，通过限定力学试验机的位移进行，通过传感器测量压入过程中的压力大小。实验中按照仿真数据，加工了五个样件，每个样件随机编号，将样件放到夹具上，放稳并确定电机壳体没有翘曲。

实验后的数据如图17所示。从图17中可以得出，实验过程中，材料没有表现出非线性变形，壳体在压缩过程中表现出较为一致的线性，而仿真数据表现出一定的非线性。刀具位移为1 mm时的仿真和实验数据结果如表9所示，实验的压力值分布范围为3 215～4 783 N，实验分布范围较大。用相同位移的结果进行对比显然产生较大的误差。对实验数据进行整理，将初始的非线性段删除，取线性较好的一段数据进行拟合，在Excel中可以得到拟合曲线的线性公式，并得出斜率，就是实际位移1 mm对应的近似压力值。取斜率的平均值，通过数据分析可以得出，实际壳体下压1 mm，需要5 964.92 N的压力。仿真与实验的误差为8.5%。

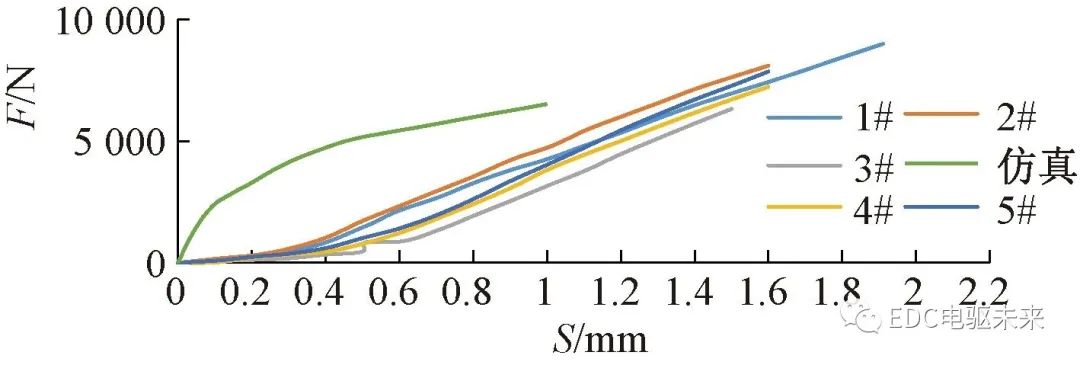
图17 实验数据与仿真数据

表9 实验数据和仿真数据压力对比

2.2 平面度测量

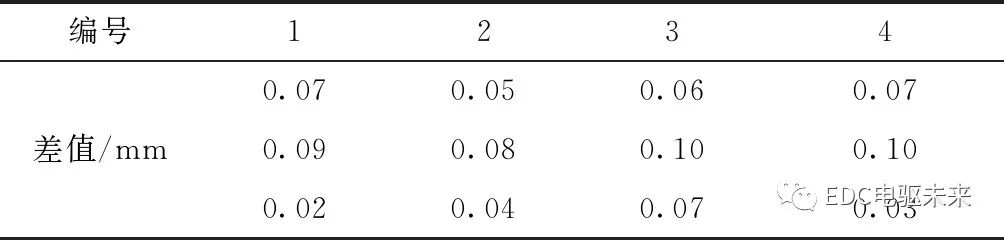
平面度测量用于检测电机壳体在进行端盖锁紧的过程中，是否发生了其他部位的变形，导致壳体扭曲或者端盖轴心偏心，影响电机质量。在实验样本中，取三个样本作为测量对象，通过对电机壳体进行四个点的平面度测量，平面度测量位置如图18，测试结果表10、表11所示。分析结果表明，锁紧卡扣前后的平面度差值在0.02～0.10 mm之间。

图18 壳体平面度测量位置

表10 实验前后壳体的平面度测量

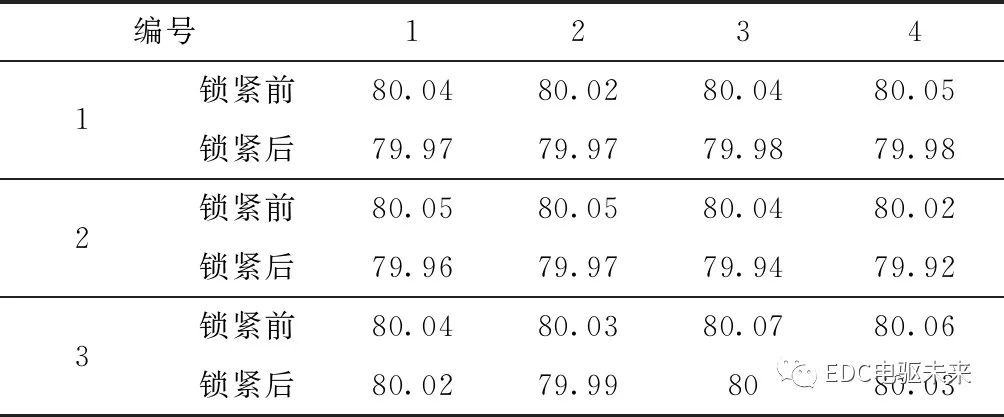
表11 实验前后的壳体变形情况

2.3 端盖推出力测量

在压紧端盖后，为了保证端盖的结构稳定，对端盖进行推出力测试。通过推力计穿过电机壳体推出端盖，从而测试卡扣结构的强度。固定电机壳体，而后沿着壳体轴向施加载荷，端盖和卡扣失效瞬间会伴随“嘭”的一声声响，得到数据如表12所示。根据表12数据，可以直观地看出，端盖在锁紧后较为坚固。

表12 端盖推出力测量

3 结 语

本文建立电机壳体锁紧卡扣的仿真模型，通过ANSYS Workbench有限元软件分析，确定了合适的刀具角度以及卡扣部分结构的尺寸，阐明了电机壳体加工过程中的重要尺寸及其影响，进行了网格无关性验证，确定合适的网格尺寸以及数量，用于快速计算求解结果，以适应工程需要。

研究结果发现：

1)电机壳体封装端盖的过程中，刀具的角度以及卡扣的尺寸对锁紧效果影响较大，材料在受到刀具压缩后，开始呈现出屈服硬化现象，并沿着设计好的方向进行塑性变形。变形过程中，变形只出现在卡扣部位，未传到电机壳体的其他部位，保证了加工的精确性。

2)虽然材料参数和实际使用镀锌钢板材料一致，但是在实际的仿真和实验中，二者也表现出了不同的性质。仿真中，材料表现出较为明显的非线性性质，并且曲线弧度较为平滑，与理想的材料力学拉伸实验曲线较为接近；实验中，材料随着刀具的下落位移增加，表现出接近线性关系的性质。且随着位移的增大，仿真的压力趋近于平缓，而实验的压力趋势仍然呈现原有线性性质。二者在相同位移的情况下，实验与仿真误差较大，对实验数据进行线性拟合后，误差在可接受范围内。由于实验中很难确定凹槽部分的具体尺寸并保证一致性，在压缩的过程中也存在其他因素干扰，无法达到仿真的理想情况。并且刀具的初始位置直接影响了实验结果，按照仿真曲线所表现出来的趋势，仿真1 mm的位移情况对应实验的位移会在1.2 mm～1.6 mm位移之间。

3)根据仿真数据进行样件制作并实验，仿真中，壳体除卡扣部分外皆无变形情况；实际的实验中，在对壳体进行端面平面度测量时，检测的三个壳体均有少量变形，变形量非常小，最大只有0.1 mm，仿真和实验有一点差异，差异在可接受范围内。端盖锁紧后的强度较高，满足生产要求。

审核编辑：郭婷