作者:Smita Choudhury 和 Abhilasha Kawle
在CTSD精密ADC系列文章的第3部分中,我们将重点介绍CTSD ADC的无混叠特性,无需添加任何外设设计即可提高对干扰源的抗扰度。第1部分展示了一类基于连续时间Σ-Δ(CTSD)架构的新型易于使用的无混叠精密ADC,可提供简单、紧凑的信号链解决方案。第 2 部分为信号链设计人员揭开了 CTSD 技术的神秘面纱。本文比较了目前可用的精密ADC架构的混叠抑制解决方案背后的设计复杂性。我们将举例说明一个理论来解释CTSD ADC架构的固有混叠抑制。我们还展示了如何简化信号链设计,并讨论了CTSD ADC的扩展优势。最后,我们将引入新的测量和性能参数来量化混叠抑制。
在声纳阵列、加速度计、振动分析等许多应用中,观察到目标信号带宽之外的信号,称为干扰源。信号链设计人员面临的主要挑战是,ADC采样现象会导致这些干扰源混叠到目标信号带宽(带内)并降低性能。除此之外,在声纳等应用中,带内混叠的干扰源可能会被误解为输入信号,从而导致声纳周围物体的误测。抑制这些混叠的解决方案是传统ADC信号链设计相当复杂的原因之一。CTSD ADC独特的固有混叠抑制特性提供了一种新的简化解决方案。在得出这个突破性的解决方案之前,本文的第一站是了解混叠的概念。
重温奈奎斯特抽样定理
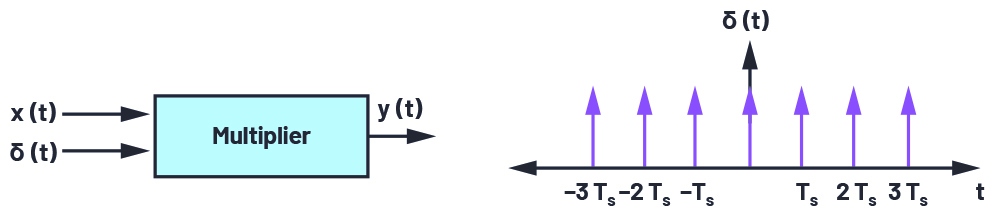
为了理解混叠的概念,让我们快速回顾一下奈奎斯特采样定理。可以在时域或频域中分析信号。在时域中,模拟信号的采样在数学上表示为信号的乘法——例如,x(t)与脉冲序列,δ(t),具有时间段Ts.
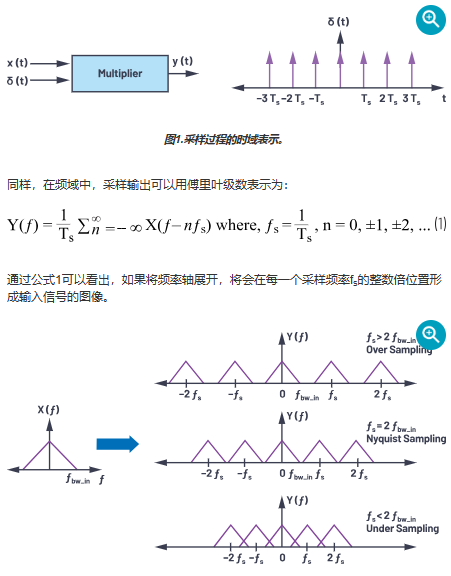
图1.采样过程的时域表示。
等效地在频域中,采样输出可以使用傅里叶级数表示为:
公式1的意思很简单,如果频率轴展开,输入信号的图像在采样频率f的每个整数倍处形成s.
图2.X(f) 通过不同采样频率采样后的表示。
公式1表明X(f)在频率f = n × f时的信号含量s, G在,其中 n = 0, ±1, ±2, ... ..., 将在 f 处表现出来在采样后,类似于图2中的欠采样场景,说明了各种条件下的采样现象。
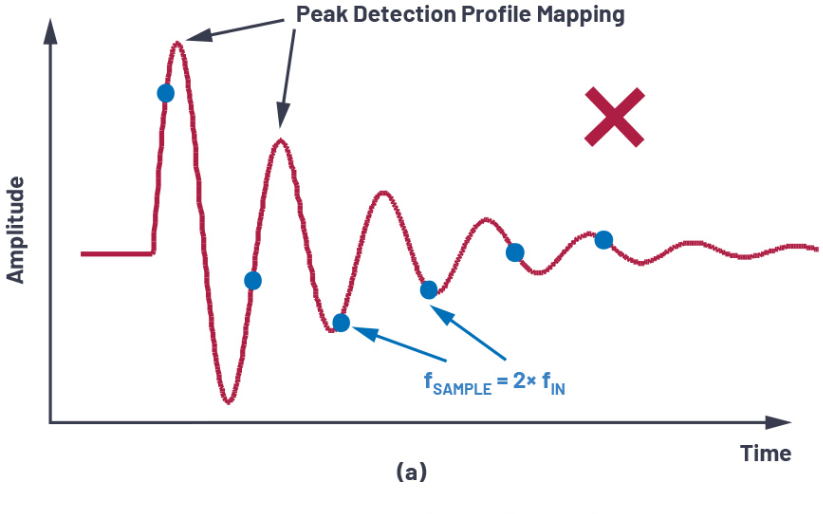
图3.(a)应用采样定理来理解混叠,(b)使用抗混叠滤波器来衰减混叠频率。
总之,奈奎斯特定理指出,任何大于采样频率一半的信号都会折叠或镜像回小于fs/2,并且可能落入感兴趣的频带。
假设ADC以频率f采样s并且系统中有两个带外音/干扰源,f1和 f2在ADC输入端,如图3所示。应用奈奎斯特定理,我们可以推断,由于音调的频率f。1小于 fs/2,采样后,其频率保持不变。虽然音调的频率f2大于 fs/2,它将在感兴趣的频带 f 中混叠自身bw_in,并降低该区域ADC的性能,如图3a所示。
该理论也可以扩展到f以外的任何噪声。s/2,它也会折返并在带内表现出来,以增加带内本底噪声并降低性能。
混叠的现有解决方案
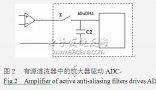
避免由于带外 (OOB) 音调或噪声折返而导致性能下降的简单解决方案是衰减超出 f 的任何信号内容sADC使用低通滤波器(称为抗混叠滤波器(AAF))进行采样之前/2。图3b显示了简单AAF的传递函数,并说明了频率f下的衰减到混叠音2在它折回带内之前。该AAF的主要特性是滤波器的阶数和–3 dB转折频率。它们由通带平坦度、特定频率(如采样频率)所需的绝对衰减以及超出输入带宽(也称为过渡带)所需的衰减斜率决定。一些常见的滤波器架构是Butterworth、Chebhesev、Bessel和Sallen-Key,可以使用无源RC和运算放大器来实现。滤波器设计工具可帮助信号链设计人员针对给定的架构和要求进行 AAF 设计。
让我们以一个示例应用程序来了解抗混叠滤波器的要求。在潜艇系统中,声纳传感器发射声波并分析水下的回波,以估计周围物体的位置和距离。传感器的输入带宽为100 kHz,系统检测ADC输入端任何>–85 dB音阶的音调作为有效的回声源。因此,来自带外的任何干扰都需要由ADC衰减至少–85 dB,以避免被声纳系统检测为输入。针对这些要求,在下一节中,我们将构建并比较不同ADC架构的别名抑制解决方案。
在逐次逼近寄存器(SAR)和离散时间Σ-Δ(DTSD)ADC等传统ADC架构中,采样电路位于ADC的模拟输入端,表明在ADC输入之前需要AAF,如图3b所示。
AAF 对 SAR/奈奎斯特采样 ADC 的要求
SAR ADC的采样频率通常设置为模拟输入频率的两倍或四倍(f在).这种ADC的AAF需要具有超出频率f的窄过渡带在,这意味着需要一个非常高阶的滤波器。从图4可以看出,采样频率约为1 MHz的SAR ADC需要一个五阶巴特沃兹滤波器,以便在频率大于100 kHz时获得–85 dB抑制。在滤波器实现方面,随着滤波器阶数的增加,所需的无源器件和运算放大器数量也会增加。这意味着SAR ADC的AAF在信号链设计中需要大量的功耗和面积预算。
AAF 对 DTSD ADC 的要求
Σ-Δ型ADC是过采样ADC,其采样远高于模拟输入频率。AAF 设计要考虑的混叠区域为 fs± f在.滤波器的过渡带要求从f在到非常高的Fs.与 SAR ADC AAF 相比,这是一个更宽的过渡带,表明所需的 AAF 阶数也较低。图4显示,对于6 MHz采样频率DTSD ADC,对于f左右的频率,要获得–85 dB抑制。s– 100 kHz,通常需要二阶 AAF。
在实际场景中,干扰源或噪声可能位于频带中的任何位置,而不限于采样频率f附近s.任何小于 f 的频率音调s/2,类似于频率f的音调1在图3中,不会表现为带内以降低ADC性能。虽然 AAF 可能会衰减音调 f1在某种程度上,它仍然存在于ADC输出中,是必须由外部数字控制器处理的不必要的信息。是否可以进一步衰减此音调,使其在ADC输出端看不到?一种解决方案是使用具有超出频率f的窄过渡带的AAF在,但随后滤波器设计的复杂性会增加。替代解决方案是片内数字滤波器,它是Σ-Δ调制器环路的一部分。
图4.AAF 与 ADC 架构的复杂性与目标频段的复杂程度。
图5.DTSD ADC的STF,前端为AAF,后端为数字滤波器。
Σ-Δ调制器环路的数字滤波器
在Σ-Δ型ADC中,由于过采样和噪声整形,调制器输出包含大量冗余信息,因此需要外部数字控制器进行大量处理。如果对调制器数据进行平均、滤波并以较低的输出数据速率(ODR)提供,则可以避免这种冗余信息处理,ODR通常为2 × f在.抽取滤波器用于将采样率从fs到所需的较低 ODR。使用数字滤波器的采样速率转换将在以后的文章中进行解释,但这里的关键点是分立时间Σ-Δ调制器通常与片内数字滤波器配合使用。干扰源的组合信号传递函数(TF)与调制器前端的模拟滤波器和后端的数字滤波器如图5所示。
总之,DTSD ADC 的 AAF 是基于混叠区域 f 周围音调所需的衰减而设计的s.以及非锯齿区域中的音调,例如 f1被片内数字滤波器完全衰减。
后端数字滤波器与前端模拟滤波器
SAR ADC在AAF中需要窄过渡带,而Σ-Δ型ADC在数字滤波器中需要窄过渡带。数字滤波器功耗低,易于集成在片上。此外,数字滤波器的阶数、带宽和过渡带的编程比模拟滤波器简单得多。
过采样的优势在于,它允许在后端使用宽转换模拟滤波器和窄转换数字滤波器,从而在功率、空间和抗干扰源方面提供优化的解决方案。
使用DTSD ADC时,AAF要求虽然放宽,但增加了设计复杂性,以满足每次采样事件后的建立时间要求,从而避免信号链性能下降。信号链设计人员面临的挑战是微调AAF,以在混叠抑制和输出建立要求之间取得平衡。
新型精密CTSD ADC无需前端模拟滤波器设计,简化了信号链设计。
CTSD ADC的固有别名抑制
在本系列的第2部分中,由闭环电阻反相放大器构建了一阶CTSD调制器,如图6所示。CTSD调制器遵循与DTSD调制器相同的过采样和噪声整形概念,以实现所需的性能,并且具有阻性输入而不是开关电容输入。调制器构建模块包括一个连续时间积分器,后接一个对积分器输出进行采样和数字化的量化器,以及一个在输入端闭合环路的反馈DAC。量化器输入端的任何噪声都是由积分器的增益传递函数形成的噪声。
图6.(a) CTSD调制器环路的构建模块和(b)用于数学分析的简化模块表示。
扩展第 2 部分的信息,可以使用以下数学模型绘制 CTSD 调制器环路的简化块表示:
积分传递函数概括为H(f),也称为环路滤波器。对于一阶积分器,H(f) = 1/2πRC 。
ADC的功能是采样和量化。因此,用于分析的简化ADC模型使用采样器,然后使用加性量化噪声源。
DAC是一个模块,它将当前时钟周期中的输入乘以一个常数。因此,它是一个具有脉冲响应的块,在采样时钟周期内恒定,其余时间为 0。
这些简化模型的等效框图如图6b所示,广泛用于Σ-Δ性能分析。来自 V 的传递函数在到 V外称为信号TF(STF)和Qe输出称为噪声TF(NTF)。
关于CTSD调制器环路固有的混叠抑制特性,一种合理的解释是,采样不是直接发生在调制器的输入端,而是在环路滤波器H(f)之后发生,如图6a所示。但是为了获得完整的图片,将使用没有采样器的线性模型来理解概念,并且分析将扩展到与采样器循环。
第 1 步:使用线性模型进行 STF 和 NTF 分析
为了简化分析,忽略采样器,线性模型如图7所示。此循环的 STF 和 NTF 可以表示为
根据公式3,STF可以改写为:
感兴趣的频率带宽是低频,因此在数学上它可以表示为f→0,而高频可以表示为f→∞。绘制时,STF 和 NTF 的幅度(以 dB 为单位)与频率的函数关系如图 7 所示。
图7.(a) 用于简化分析的线性模型和 (b) STF(f) = H(f) × NTF(f)。
图8.(a) 输入 = 0 V 的 CTSD 调制器环路图和 (b) 调制器环路的 NTF。
图9.调制器环路的重新排列,以说明固有的混叠抑制。
NTF 类似于高通滤波器,STF 类似于低通滤波器,目标频段的幅度为平坦的 0 dB,较高频率的衰减相当于 AAF TF。在数学上,信号通过具有高增益、低通滤波器配置文件的H(f),然后由NTF环路处理。现在,通过首先了解NTF块表示,可以将这种理解扩展到与采样器一起循环。
步骤 2:NTF 的框图表示
带输入 V在设置为0 V,调制器环路的框图可以如图8a所示重新排列,并用于NTF表示。当采样器处于循环中时,NTF 响应将类似于线性模型,但每 f 的倍数处都有复制的图像s,如图 8b 所示。
第 3 步:重新排列调制器环路以可视化前期滤波动作
如果将环路滤波器H(f)和调制器环路的采样器移至输入端,并且反馈如图9所示,则从输入到输出的传递函数没有变化。此重新排列的框图的右侧表示 NTF。
与步骤1中的线性模型类似,在采样等效系统中,输入信号遍历高增益H(f),然后通过NTF环路进行采样和处理。信号通过环路滤波器的横向在采样之前会创建一个低通滤波器配置文件。该配置文件导致CTSD调制器的固有混叠抑制。因此,CTSD调制器环路的STF如图9所示。
第 4 步:使用数字滤波器完成 STF
为了减少冗余高频信息,CTSD调制器与片内数字抽取滤波器配合使用,组合混叠抑制TF如图10所示。来自 f 周围的别名s由CTSD固有的混叠抑制特性衰减,而中间干扰源则由数字滤波器衰减。
图4比较了SAR ADC、DTSD ADC和CTSD ADC在采样频率下–80 dB抑制所需的AAF阶数与输入信号带宽。带有SAR ADC的AAF的阶次和复杂性最高,而CTSD ADC不需要外部AAF,因为混叠抑制是其设计固有的。
CTSD架构带来的信号链优势
在某些多通道应用中,如声纳波束成形和振动分析,通道之间的相位信息非常重要。例如,通道之间的相位需要精确匹配,要求在20 kHz时为0.05°。
对于传统的ADC信号链,AAF采用无源RC和运算放大器设计。滤波器在带内引起一定的幅度和相位下降,这是转折频率的函数。为了获得良好的通道间相位匹配,所有通道都需要具有相同的下降,这表明需要精细控制和匹配每个通道的滤波器转折频率。二阶巴特沃兹滤波器,设计用于在16 MHz(采样频率)和f频率下实现–80 dB抑制3分贝160 kHz(输入带宽)的相位失配在20 kHz时可能具有±0.15°,RC绝对值的误差容限低至1%。容错性较低的RC无源器件的可用性受到限制,并增加了物料清单(BOM)。
由于 AAF 在 CTSD ADC 信号链中被消除,因此通道间幅度和相位匹配本质上是在目标频段内实现的。相位失配受到模拟调制器环路设计的片内失配的限制,在20 kHz时可能低至±0.02°。
图 10.带有后端数字滤波器的CTSD调制器环路。
测量和量化固有的别名拒绝
AD4134的ADC数据手册中介绍了用于测量别名抑制的新功能检查,AD4134是一款基于CTSD ADC架构的精密ADC。对ADC的模拟输入信号的频率进行扫描,并通过测量测试频率折回的音调幅度(如果有的话)相对于所施加音调的幅度来计算每个带外输入信号的影响。
图11显示了AD4134在性能带宽为160 kHz、采样频率为24 MHz时带外频率下的混叠抑制。对于 23.84 MHz (fs– 160 kHz),混叠抑制为 –85 dB,这是 ADC 的混叠抑制规格。还可以观察到,对于其他中频,抑制优于–100 dB。有关固有混叠抑制以及进一步提高这种抑制的选项的更多详细信息,请参见AD4134数据手册。
图 11.混叠抑制与带外频率的关系。
到目前为止介绍的CTSD ADC概念可以帮助信号链设计人员设想该架构的阻性输入、阻性基准电压源和固有混叠抑制的独特特性。易于驱动的输入和基准电压源,加上CTSD ADC信号链的AAF设计,为各种应用带来了新的简化ADC前端设计。
审核编辑:郭婷
-
传感器
+关注
关注
2551文章
51084浏览量
753416 -
滤波器
+关注
关注
161文章
7811浏览量
178077 -
adc
+关注
关注
98文章
6498浏览量
544577
发布评论请先 登录
相关推荐
抗混叠滤波器设计的3条指导原则
ADC应用领域中的混叠简介
AD6676的优缺点分析 ∑-∆型ADC的意义何在?
连续时间Σ-Δ型ADC的优势介绍
ADC抗混叠滤波与驱动问题
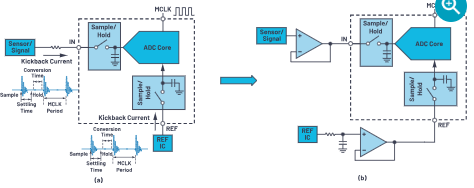
简化ADC输入和基准驱动,简化信号链设计
面向信号链设计人员的CTSD架构详解
深入分析信号链设计,助你了解CTSD技术的关键优势
CTSD精密ADC:轻松驱动ADC输入和基准电压源,简化信号链设计




 CTSD ADC架构的固有混叠抑制及如何简化信号链设计
CTSD ADC架构的固有混叠抑制及如何简化信号链设计


























评论