面向信号链设计人员的CTSD架构详解

本文将以不太传统的方法解释连续时间Σ-Δ（CTSD）ADC技术，使信号链设计人员能够设想一类新型易于使用的精密ADC技术，作为互连几个知名组件的简单系统。在第1部分中，我们重点介绍了现有信号链设计面临的主要挑战，这些挑战可以通过精密CTSD ADC显著简化，因为它在保持连续时间信号完整性的同时实现了最高精度。现在，问题是CTSD架构背后的是什么使其能够实现这些优势？

解释CTSD技术概念的传统方法是首先了解离散时间Σ-Δ（DTSD）调制器环路的基础知识，然后用等效的连续时间元件替换离散时间环路元件。虽然这种方法可以深入了解Σ-Δ功能，但我们的目标是更直观地了解精密CTSD ADC的固有优势。首先，我们将概述构建CTSD调制器环路的分步方法，从广为人知的闭环反相放大器配置开始，并将其与ADC和DAC相结合。最后，我们将评估我们构建的电路的基本Σ-Δ功能。

步骤1：重新审视闭环反相放大器配置

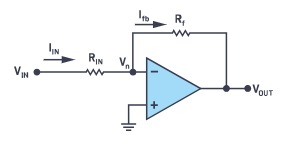
CTSD ADC的主要优势之一是，它提供易于驱动的连续阻性输入，而不是传统的前期开关电容采样器。具有类似输入阻抗概念的电路之一是反相放大器，我们将将其用作构建CTSD调制器环路的起始模块。

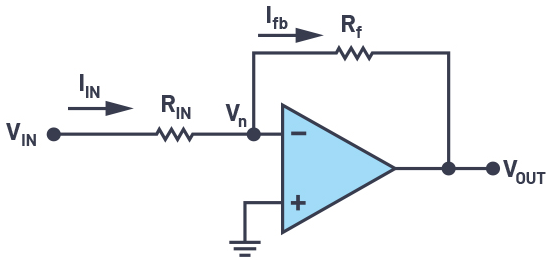
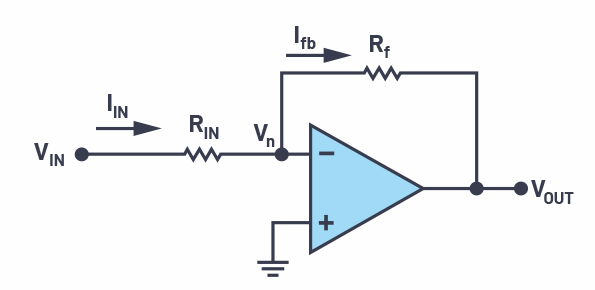
闭环运算放大器配置一直是复制高保真模拟输入的首选，图1显示了最流行的运算放大器配置之一，称为反相放大器配置。1保真度的度量之一是输出到输入增益，在Σ-Δ命名法中也称为信号传递函数（STF）。确定影响STF的参数需要分析电路。

图1.采用反相放大器配置的闭环运算放大器。

为了更新我们的数学技能，让我们重新审视著名的V的推导外/V在.第一步，假设运算放大器A的开环增益为无穷大。该假设直接导致运算放大器V的负输入n在潜在的地面。基尔霍夫定律在这个节点的应用给出了

将其映射到 V外和 V在，我们得到的增益或 STF 为

接下来，让我们超越不切实际的无限增益假设，用运算放大器的有限增益A重新推导STF。STF 现在看起来像

从这里开始，教科书通常描述对每个参数R的灵敏度在， Rf和 A。对于我们的案例，让我们继续构建 CTSD 循环。

第2步：在放大器中引入离散化

我们的ADC信号链要求是V的数字化版本在.在下一步中，我们将介绍该电路中的数字化。与其使用将采样ADC直接放在输入信号上的传统方式，不如尝试不同的方法，在放大器输出之后放置一个代表性ADC，以获得数字化数据。但ADC的输出不能直接用作反馈，因为它必须是模拟电压。因此，我们需要使用电压数模转换器（DAC）跟踪ADC，如图2所示。

图2.在反相放大器配置中引入ADC和DAC。

由于ADC和DAC，V外仍然是 V 的表示在但由于添加了数字化而导致量化错误。因此，来自 V 的信号流没有任何变化在到 V外.这里需要注意的一点是，为了使环路的功能对称于0 V左右并简化我们的数学推导，选择ADC和DAC的基准电压源为

第 3 步：介绍模拟累加器 – 积分器

图2中的闭环配置是否稳定？ADC和DAC都是采用采样时钟MCLK工作的离散化元件。对于转换器专家来说，设计无延迟ADC或DAC一直是无法实现的梦想。由于这些环路元件是时钟的，因此输入通常在一个边沿采样，并在另一个时钟边沿进行处理。因此，ADC和DAC组合V的输出外，即图 2 中的反馈，仅在 1 个时钟周期延迟后可用。

反馈的延迟对稳定性有什么影响吗？让我们追踪 V 如何在转移。为了简化起见，我们假设 V在= 1， R在= 1， Rf= 1，运算放大器A的增益为100。在第一个时钟周期，输入电压为1，DAC输出反馈为V外或 V奥特达克为 0，直到下一个时钟边沿才可用。当我们跟踪放大器和ADC输出的输入和反馈之间的误差时，我们可以看到输出保持指数增长，这在技术上称为失控问题。

	V在	V外= V奥特达克	Vn= （V外+ V在） ⁄2	VOUT_INT= – × （Vn)	D奥塔德克
第一个样品边缘	1	0	0.5	–50	–50
第二个样品边缘	1	–50	~ –25	~2500	2500
第三个样品边缘	1	2500	~1250	~–12，500	–12,500

这是因为ADC输入在放大器获得的瞬时误差下工作;也就是说，ADC甚至在反馈可用之前就做出决定，这不是必需的。如果ADC处理累积的平均误差数据，以便平均反馈的1时钟延迟引起的误差，则系统的输出将被限制。

积分器是平均累加器的一个模拟等效物。环路的增益仍然很高，但仅在低频下，或者换句话说，在目标频率带宽下。这可确保ADC不会出现任何可能导致失控情况的瞬时误差。因此，环路现在由放大器修改为积分器，然后是ADC和DAC，如图3a所示。

图3.（a） 将积分器引入循环。（b） 重新安排循环以突出显示D奥塔德克作为输出。

第4步：简化反馈电阻

我们感兴趣的元素是D奥塔德克，所以让我们重新排列循环元素以突出显示 D奥塔德克作为系统的输出，如图3b所示。接下来，让我们参观一下DAC和R的简化f路径。为此，让我们深入了解DAC的细节。DAC的目的是转换数字代码D在，与基准成比例的等效模拟电流或电压。为了进一步扩展基准电压源连续性的优势，我们在这里考虑的是一种基于基准电压源上没有开关负载的电阻梯形图的通用DAC架构。让我们回顾一下温度电阻DAC，2转换 D在DAC电流，与公式5有关。

其中 V裁判= V参考文献– V参考文献，DAC两端的总基准电压。

D在= 温度代码中的数字输入

Rf= 反馈电阻;拆分为每个单元元素

N = 位数

图4.一般的温度电阻式DAC。

为了获得电压输出，在跨阻配置中使用运算放大器进行I至V转换，3如图4所示。所以

回到图3b的离散化循环，这个V奥特达克再次转换回当前，IFB，通过反相放大器的反馈电阻，暗示信号流为I代数转换器→ V奥达 C→ IFB.数学

从上面的信号流和公式中，我们看到转换 V奥特达克到我FB是可以绕过的冗余步骤。删除冗余元素，为简单起见，表示 （V参考文献– V参考文献） 作为 V裁判，让我们重绘循环，如图 5 所示。

图5.去掉多余的I至V和反馈电阻。

瞧！我们已经构建了一个一阶Σ-Δ循环！所有这些都是通过将众所周知的元件（反相放大器、ADC 和 DAC）拼接在一起来实现的。

步骤 5：了解过采样

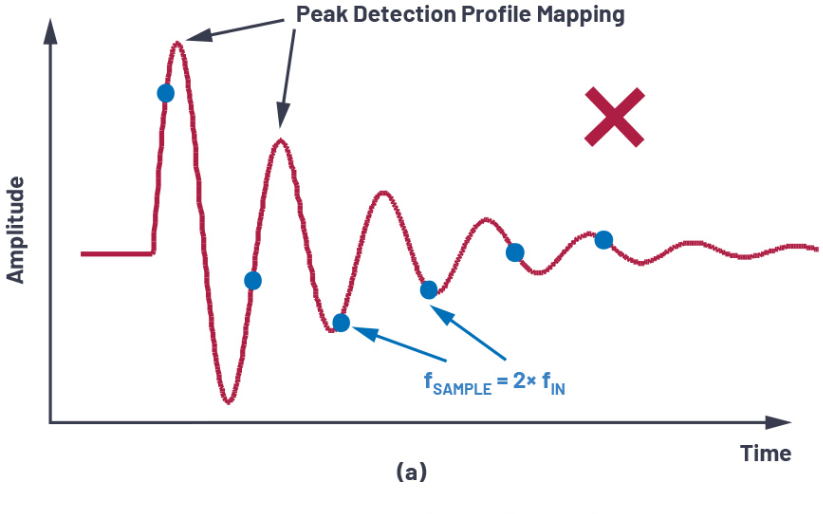
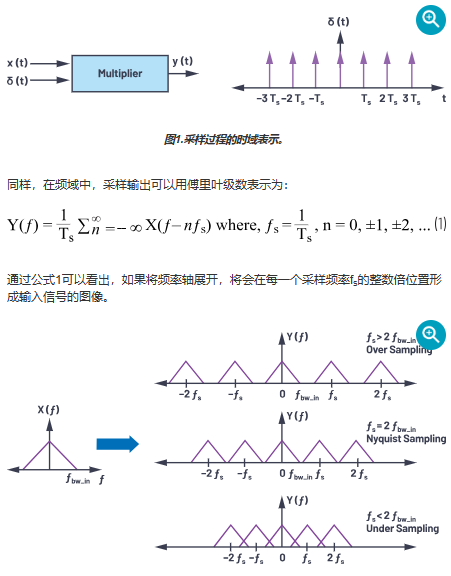
到目前为止，我们已经掌握了CTSD循环的构建，但我们还没有意识到这个奇特循环所提供的特殊性。实现这一目标的第一步是理解过采样。仅当有足够的采样和数字化数据点来提取或解释模拟信号信息时，ADC数据才有用。奈奎斯特定理建议，为了忠实地重建输入信号，ADC的采样频率应至少是信号频率的两倍。如果我们在这个最低要求上继续添加更多的数据点，解释中的错误将进一步减少。按照这种思路，在Σ-Δ中，选择的采样频率远高于建议的奈奎斯特频率，这称为过采样。过采样4通过将总噪声分散到更高的频率上，有助于降低目标频段的量化噪声，如图6所示。

图6.奈奎斯特采样和过采样之间的噪声频谱密度比较。

第 6 步：了解噪声整形

当Σ-Δ专家使用噪声传递函数（NTF）或噪声整形等术语时，信号链设计人员不应感到迷茫，4我们的下一步将帮助他们直观地理解这些术语，因为它们是Σ-Δ转换器命名法所独有的。让我们重新审视一下简单的反相放大器配置，并引入误差Qe在放大器的输出端，如图7所示。

图7.在反相放大器配置中引入误差。

该误差在输出端的贡献量化为

数学公式翻译为误差 Qe被放大器的开环增益衰减，这只是重申了闭环的优势。

这种对闭环优势的理解可以扩展到量化误差QeCTSD环路中的ADC，这是由于积分器输出端连续信号数字化而引入的误差，如图8所示。

图8.在Σ-Δ循环中引入量化误差Qe。

我们现在可以直观地得出结论，这个Qe将被积分器衰减。集成商 TF |H英特格（f）|= 1/|s × RC|= 1/2πfRC及其对应的频域表示如图9所示。其曲线相当于低频时具有高增益的低通滤波器曲线，增益随频率增加线性降低。相应地，Q 的衰减e然后看起来像一个高通滤波器。

图9.积分器传递函数。

该衰减因子的数学表示是噪声传递函数。暂时忽略ADC中的采样器和DAC中的开关。The NTF, V奥塔德克⁄ 问e，可以按照与反相放大器配置相同的练习进行评估，反相放大器配置在频域中看起来像一个高通滤波器曲线，如图10所示。

在感兴趣的频带中，量化噪声被完全衰减并推到“不关心”的高频。这就是所谓的噪声整形。

图 10.无需采样器的噪声传递功能—具有高通滤波器配置文件。

当采样器处于循环状态时，量化噪声整形类比保持不变。不同之处在于NTF频率响应将以f的每倍复制图像S，如图10所示，从而在采样频率的每个整数倍处产生陷波。

图 11.CTSD ADC的噪声传递函数。

Σ-Δ架构的独特之处在于，在粗制型ADC（例如4位ADC）周围放置积分器和DAC环路，并应用过采样和噪声整形的概念，可显著降低目标频率带宽中的量化噪声，并将该粗制ADC屏蔽为16至24位精密ADC。

一阶CTSD ADC的这些基础知识现在可以扩展到任何阶次的调制器环路。采样频率、粗略的ADC规格和环路顺序是由ADC的性能要求驱动的顶层设计决策。

第 7 步：使用数字滤波器完成 CTSD 调制器

通常，在ADC信号链中，数字化数据由外部数字控制器进行后处理，以进行任何信号信息提取。正如我们现在所知，在Σ-Δ架构中，信号被过采样。如果将这种过采样的数字数据直接提供给外部控制器，则需要处理大量冗余数据。这会导致数字控制器设计中的超大功率和空间成本开销。因此，在将数据呈现给数字控制器之前，数据样本会以有效的方式丢弃，而不会影响性能。这个过程称为抽取，由数字抽取滤波器完成。图11所示为带有片内数字抽取滤波器的典型CTSD调制器。

图 12.（a） 从模拟输入到数字输出的CTSD ADC调制器环路框图。（b） 调制器输出端和数字滤波器输出端输入信号的频谱表示。

图12b显示了带内模拟输入信号的频率响应。在调制器的输出端，我们观察到量化噪声的噪声整形，从而在目标频带内大幅降低其。数字滤波器有助于衰减超出目标频率带宽的整形噪声，以便在最终数字输出处，D外，处于奈奎斯特采样率。

第 8 步：了解 CTSD ADC 的时钟灵敏度

到目前为止，我们已经了解了CTSD ADC如何保持输入信号的连续完整性，从而大大简化了信号链设计。这种架构也有一些限制，主要处理采样时钟MCLK。CTSD调制器环路的工作原理是将I之间的误差电流积分在和我代数转换器.该积分值中的任何误差都会导致ADC在环路对误差进行采样，并将其反映在输出中。对于我们的一阶积分器环路，采样时间段内的积分值为 Ts对于常数 I在和我代数转换器由

对于输入 0，影响此积分错误的参数为

MCLK频率：如公式10所示，如果MCLK频率缩放，则控制积分斜率的RC系数也需要重新调谐，以获得相同的积分值。这意味着CTSD调制器针对固定的MCLK时钟频率进行调谐，并且不能支持不同的MCLK。

MCLK 抖动：DAC 代码，因此 I代数转换器更改每个时钟时间段 Ts.如果 I代数转换器时间段随机变化，然后平均积分值不断变化，如图 13 所示。因此，采样时钟时间段中的任何抖动形式的错误都会影响调制器环路的性能。

图 13.CTSD 调制器的时钟灵敏度。

由于上述原因，CTSD ADC对MCLK的频率和抖动很敏感。5但ADI已经确定了解决这些谬误的解决方案。例如，沿系统生成精确、低抖动MCLK并将其路由到ADC的挑战，可以使用ADC附近的本地低成本晶体和振荡器来解决。通过使用创新的异步采样速率转换（ASRC），该转换可以为数字控制器提供可变且独立的数字输出数据速率，而与固定采样MCLK无关，从而解决了围绕固定采样频率的谬误。有关此内容的详细信息将在本系列的后面部分详细介绍。

第 9 步：瞧！一切都准备好向你的伙伴们解释CTSD的概念！

第1部分重点介绍了CTSD ADC的某些信号链优势，第2部分重点介绍了使用闭环运算放大器配置概念构建的从步骤1到步骤6构建的调制器环路。图11a也帮助我们可视化了这些优势。

CTSD ADC的输入阻抗相当于反相放大器的输入阻抗，具有阻性且易于驱动。使用创新技术，调制器环路DAC使用的基准电压源也采用阻性。ADC的采样器位于积分器之后，而不是直接位于输入端，这使得目标频带外的干扰源能够实现固有的混叠抑制。在本系列的下几篇文章中，我们将深入探讨这些优势中的每一个及其对信号链的相应影响。在下一篇文章中，我们将从最独特的优势开始：固有的别名抑制。请关注第3部分，了解固有混叠抑制，并使用AD4134首次引入的一组基于CTSD架构的新型测量和性能参数来进一步了解其量化。

审核编辑：郭婷