统计压缩编码机理分析（上篇）-电子发烧友网

文章转发自51CTO【ELT.ZIP】OpenHarmony啃论文俱乐部——《统计压缩编码机理分析》

1.技术DNA

2. 智慧场景

场景	技术	开源项目
自动驾驶 / AR	点云压缩	Draco/ 基于深度学习算法/PCL/OctNet
语音信号	稀疏快速傅里叶变换	SFFT
流视频	有损视频压缩	AV1/H.266编码/H.266解码/VP9
GPU 渲染	网格压缩	MeshOpt/Draco
科学、云计算	动态选择压缩算法框架	Ares
内存缩减	无损压缩	LZ4
科学应用	分层数据压缩	HCompress
医学图像	医学图像压缩	DICOM
数据库服务器	无损通用压缩	Brotli
人工智能图像	人工智能图像压缩	RAISR
文本传输	短字符串压缩	AIMCS
GAN媒体压缩	GAN 压缩的在线多粒度蒸馏	OMGD
图像压缩	图像压缩	OpenJPEG
文件同步	文件传输压缩	rsync
数据库系统	快速随机访问字符串压缩	FSST
通用数据	高通量并行无损压缩	ndzip
系统数据读写	增强只读文件系统	EROFS

3.开篇简介

本文着重对传统经典压缩算法的分析与理解，从认识到实现的角度展开描述，主要涉及了 Shannon-Fano、Huffman、算术编码等编码方案。除此之外，还附带了对于数据压缩初识的部分。

3.1 统计编码是什么

统计编码（statistical compression），也可称为熵编码，其出现是为了弥补传统VLC可变长编码在编码时须进行特定方法匹配的痛点，原因是VLC有时并非能找到最佳选择，相较来说，统计编码是一类只需依据每个字符出现的次数 / 概率，便可自生成一套高效编码的方案，正因如此，它们具备显著的通用性。

统计编码的首要目的是，在信息和码之间找到明确的一一对应关系，从而保证在解码时准确无误地再现回来，或极接近地找到相当的对应关系，同时将失真率控制在一定范围内。但无论借助什么途径，核心总是要把平均码长 / 码率压低到最低限度。

3.2统计编码分类

四种常用的统计编码有：香农·范诺编码、Huffman 编码、算术编码以及 ANS，其中，香农·范诺编码称得上是现代第一个压缩编码，具有相当的历史意义。

4.香农·范诺编码

4.1诞生背景

早在香农（Claude Elwood Shannon）撰写《通信的数学理论》一文，并试图提出且证明一种可以按符号出现概率实现高效编码，以最大程度减少通信传输所需信道容量的方法之前，时任 MIT 教授的罗伯特·范诺（ Robert Mario Fano ）也已对这一编码方法展开了相关研究。范诺不久后将其以技术报告的形式独立进行了发表，因而，这种编码被并称为香农·范诺编码（ Shannon–Fano coding ），它是现代熵编码与数据压缩技术的雏形。即便它不是最佳的编码方案，但在有些时候仍会使用。

4.2简单认识

香农·范诺编码准确的说是一种前缀码技术，所谓前缀码，是指编码后的每个码字都不会再作为其他码字的前缀出现，这为后续解码操作时字符的唯一确定提供了条件。

以EBACBDBEBCDEAABEEBDDBABEBABCDBBADBCBECA这样一串字符串为例，我们首先需要统计并计算其中每个字符的出现概率。

字符	A	B	C	D	E
计数	7	14	5	6	7
概率	0.179	0.359	0.128	0.154	0.179

下一步，将它们按照概率大小降序排列：

字符	B	A	E	D	C
计数	14	7	7	6	5
概率	0.359	0.179	0.179	0.154	0.128

然后，找到这样一个两字符之间的最佳分割点，它使两侧概率和尽可能接近，也就是差值最小，反复进行下去：

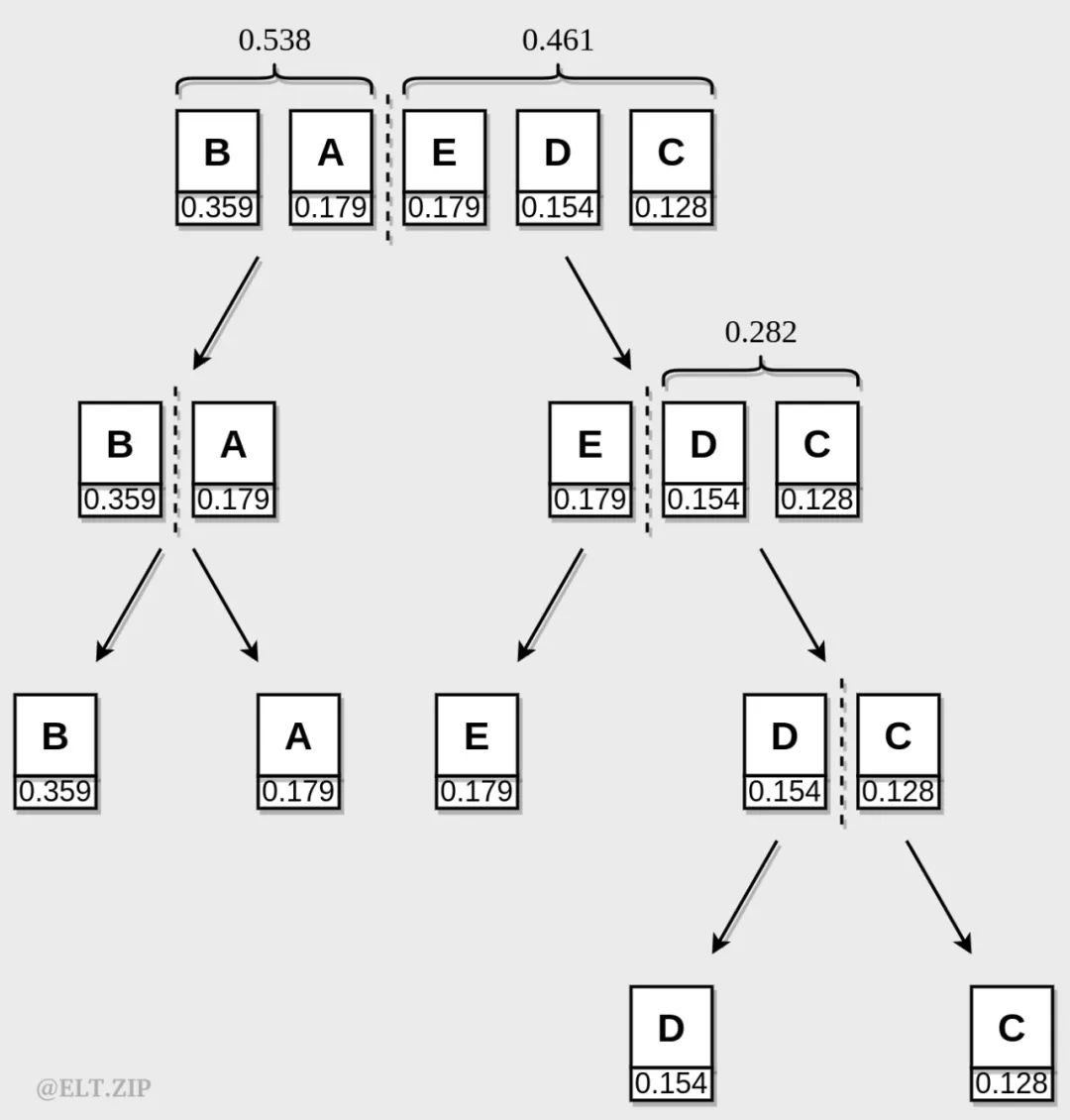
经以上操作分组完毕后，五个字符已位于整棵树的最外层叶子处，在每个分支处的左半部分树干标上 0，右半部分树干标上 1。最后，从树根起始，沿树干依次遍历至最外层的叶子节点，便得到了每个字符的香农·范诺码。由于每个树干的 “0”、“1” 二进制码独一无二，所以最终的编码彼此不会重复。

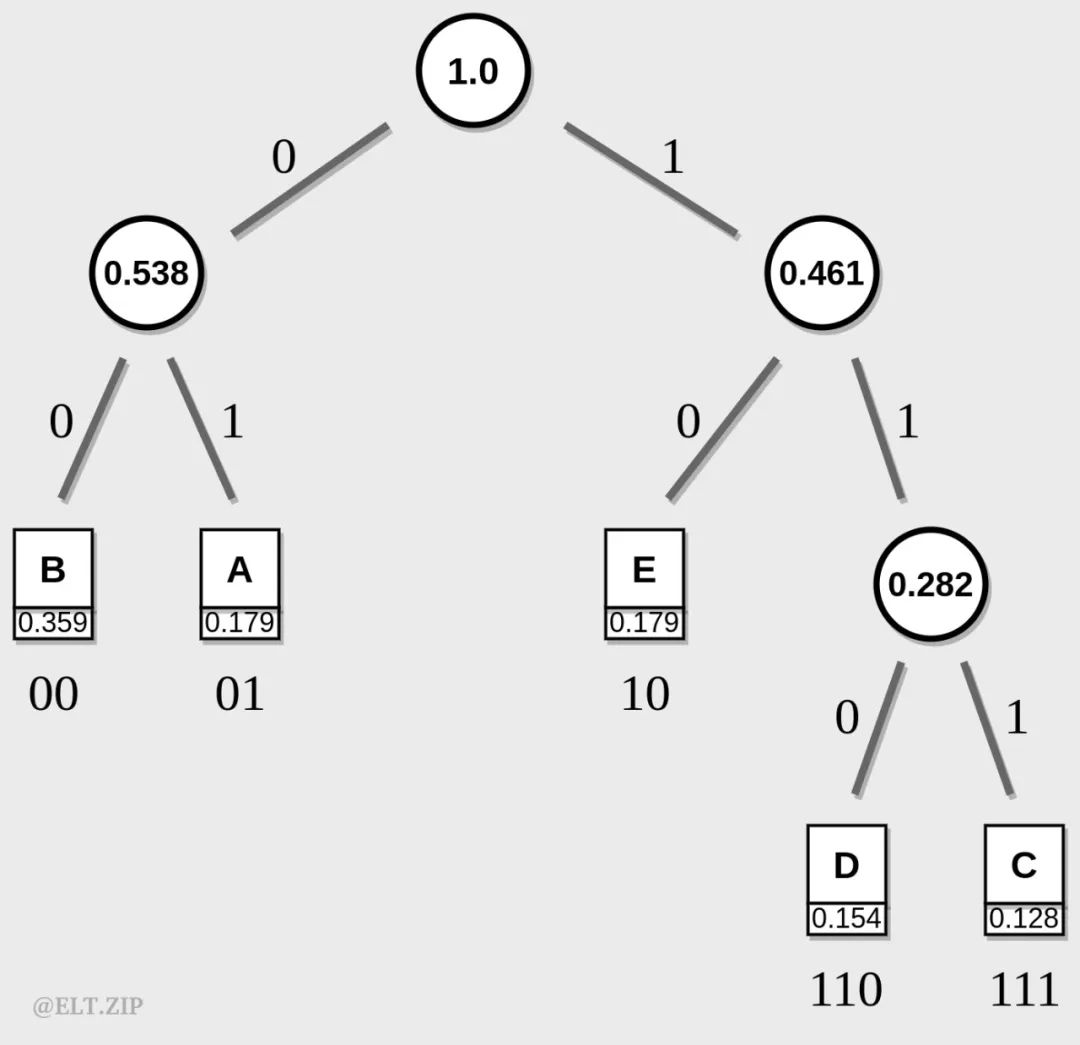
符号	A	B	C	D	E
计数	7	14	5	6	7
编码	1	0	111	110	10

出现概率较高的字符被编码成两位，概率较低的则被编码成三位。由此，我们便可计算出每个字符平均所需的编码位数：

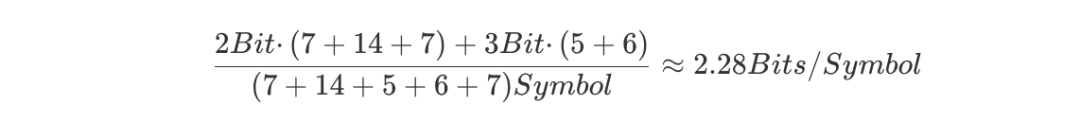
结果表明，每个字符平均只需约 2.28 个位即可保证在信息不丢失的情况下完美表示。当然，实际在计算机中，是无法把位分割成小数的，2.28 需二次近似于 3。

然而迄今为止，仍没有任何一种编码方案能够保证在通用情况下达到香农熵值。香农与范诺两位杰出科学家为后世压缩技术的发展开了一个好头。

5.哈夫曼编码

香农·范诺编码固然强大，但它并非总是能产生最优前缀码，所以只能取得一定的压缩效果，离真正实用的压缩算法还相去甚远。

为此，在其基础上演化出的第一个称得上实用的压缩编码哈夫曼编码（ Huffman Code ），由大卫·哈夫曼（ David Albert Huffman ）于 1952 年的博士论文《最小冗余度代码的构造方法（ A Method for the Construction of Minimum Redundancy Codes ）》中提出。哈夫曼编码同样依据字符使用的频率来分配表示字符的码字，不同的是，频繁出现的字符被分配较短的编码，出现不是那么频繁的字符则会被分配较长的编码。

哈夫曼编码效率高、运算速度快、实现方式灵活。自 Windows10 起所支持的 CompactOS 特性，便是利用哈夫曼压缩来减小操作系统体积的一项技术。直至今天，许多《数据结构》教材在讨论二叉树时仍绕不开哈夫曼这样一个话题，不过，比起算法本身，最为人们津津乐道的还是发明算法的过程。

5.1青出于蓝而胜于蓝

1951 年，哈夫曼作为一名 MIT 的学生，正在上一门由导师范诺教授的《信息学》课程。不过，既然正式上了一门课，那期末考核是在所难免的。范诺出了道选择题，给学生们两种通过考核的方式：第一选项是夜以继日地照常复习，最后参与期末考试；第二选项是完成期末论文，也被叫做大作业。同学们普遍认为，在 MIT 这样一个地方，考试的难度可不是个小儿科，尽管如此，比起要求逻辑严谨、证明充分的学科论文来说，大多数同学还是更倾向于去考试。哈夫曼选择了不随波逐流，他认为后者相对于他而言更简单，又能逃脱考试的浩劫，何乐而不为？

不出所料，最终只有哈夫曼一人选择了独自开辟新路径 —— 范诺限定了这样一个课题：“给定一组字母、数字或其他各种符号，设法找到其最有效的二进制编码”。实际上，这即是范诺与香农等大科学家所正在研究的内容，是信息论与数据压缩领域尚未解决的难题，但他并未告诉学生们这一点。

结合所学知识，哈夫曼知道“最有效”一词的意思是“编码长度足够短”。起初，哈夫曼认为这个问题应该不是什么难事，渐渐地，他发现事情其实远并非他想得那样。经过几个月的苦思冥想与文献查找，哈夫曼确实设计出了许多算法，但令人沮丧的是，没有一种算法可以被证明达到了“最有效”的条件…… 到了学期结束的前一周，仍旧没有取得任何实质性突破，哈夫曼开始为之感到疲倦。迫于即将结课的压力，他不得不撂掉手头上这已不可能完成的任务，回头转向为常规考试的准备。一天早餐后，就在哈夫曼随手抓起桌上的研究笔记将其扔进废纸篓之时，一切突然明朗了起来，他说那是他生命中最奇特的时刻。这样一个困扰领域专家许久的难题，被一个年仅 25 岁的小伙子当作课程作业给解决了。

哈夫曼后来回忆道，如果他知道他的老师和信息学之父彼时也都在努力解决这个问题，他可能永远也不会想到去尝试。他很庆幸自己在正确的时间做了正确的事，庆幸他的老师在那时没有告诉他还有其他更优秀的人也曾在这个问题上苦苦挣扎。

5.2编码方法

哈夫曼编码是分组编码、可变长编码，是依据各字符出现的概率构造码字的。制作码表的基本原理是基于二叉树的编码思想：所有可能的输入字符在哈夫曼树上对应为一个叶子节点，节点的位置就是该字符的哈夫曼编码。其次，基于字符串中每个字符的累计出现次数进行编码，出现频率越高得到的编码越短。特别的，为了构造出唯一可译码，这些叶子节点都是哈夫曼树上的终极节点，不再延伸，不再出现前缀码。可以感受到，哈夫曼编码与香农·范诺编码的实现过程极其类似，但还是有些许不同，哈夫曼编码的大体步骤如下：

将信源消息符号按其出现的概率大小依次排列
取两个概率最小的字符分别配以 0 和 1 两个码元，并将这两个概率相加作为一个新字符的概率，与未分配二进制码的字符一起重新排队
对重排后的两个概率最小的字符重复步骤 2 的过程
不断重复上述过程，直到最后两个字符被配以 0 和 1 为止
从最后一级开始，向前返回得到各个信源符号所对应的码元序列，即相应码字

5.3举个例子

让我们浅试一下，现在有一串由 5 个不同字符 ( A, B, C, D, E ) 组成的字符串序列：

BACAB BACDA ABBBE

步骤一：根据上述字符串，统计各个字符出现的次数并排序：

字符	B	A	C	D	E
次数	6	5	2	1	1

步骤二：把次数最少的两者放在一起并相加，同时将结果按顺序重新放入队列。显然，是 D: 1, E: 1, 1 + 1 = 2。

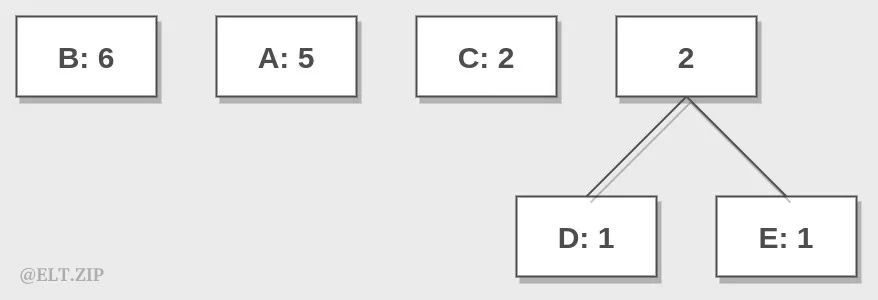
步骤三：继续抽出两个值最小的卡片，重复上一步并以此类推……

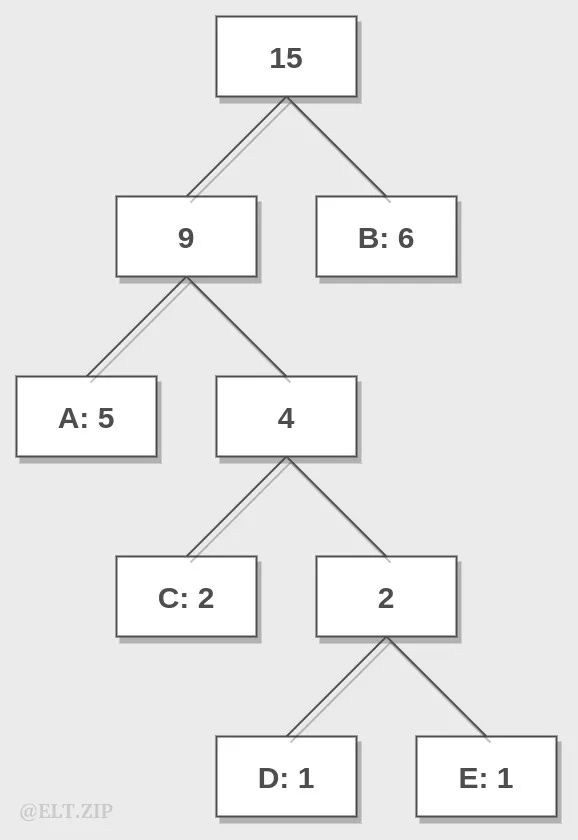
步骤四：现在，我们完成了步骤二的迭代，一棵二叉树的模型自然形成了，下面要做的就是分别在每个分支的左树干上标 0、右树干上标 1。

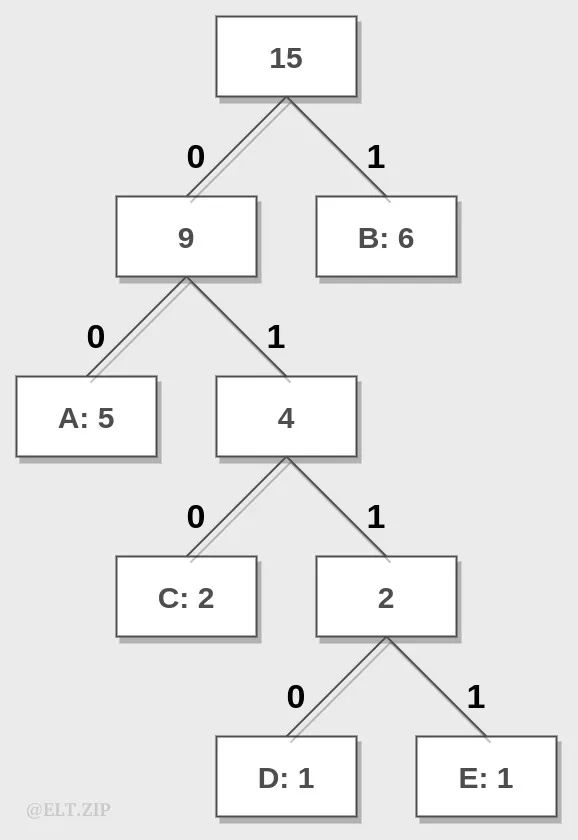
步骤五：从树根到每片叶子依次遍历，将经过的 0、1 记录下来，即可得到哈夫曼码表。

字符	B	A	C	D	E
次数	6	5	2	1	1
编码	1	0	10	110	111

所以，原本的字符串BACABBACDAABBBE用哈夫曼码表示为：100010001100010011000001110111，符合字符出现次数越多编码长度越短的标准。

5.4一些性质

与香农·范诺编码相比，哈夫曼编码的平均码长更小，编码效率高，信息传输速率大。所以在压缩信源信息率的实用设备中，哈夫曼编码还是比较常用的。哈夫曼方法得到的码并非唯一，不唯一的原因有两点：

每次对信源进行压缩时，最后分配给两个概率最小的字符以 0 和 1 可以是任意的，由此可以得到不同的哈夫曼码，但不会影响码字的长度。
对信源进行缩减时，两个概率最小的字符合并后的概率与其他信源字符的概率相等时，它们在压缩信源中放置的前后相对次序可以是任意的，由此也会得到不同的哈夫曼码。此时将影响码字的长度，一般将合并的概率放在上面，这样可获得较小的码长方差。

哈夫曼码是用概率匹配方法进行信源编码。它有两个明显特点：一是哈夫曼码的编码方法保证了概率大的符号对应于短码，概率小的符号对应于长码，充分利用了短码；二是压缩信源的最后二个码字总是最后一位不同，从而保证了哈夫曼码是即时码。

编码平均长度等式：

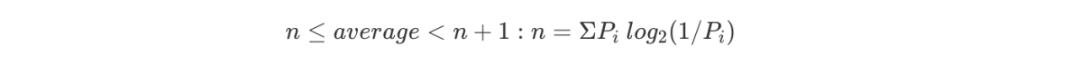
对于哈夫曼编码的基本理论，我们差不多都清楚了，下面尝试如何用代码去实现它。

5.5算法实现

哈夫曼算法的模型基于二叉树，树的节点分为终端节点（叶子节点）与非终端节点（内部节点）。为了达成一个在二叉树下更通用、标准的定义，我们将字符出现的频率抽象为权重。初始第一轮迭代时，每个最底层的节点都是叶子节点，包含两个字段：字符与权重；在第二轮及以后的迭代中，产生的每个节点都是内部节点，包含三个字段：权重、指向左子节点的链接与指向右子节点的链接。

因此，首先需要具备的两个必要元素便是内部节点与叶子节点，同时，它们又都包含权重这一相同字段，所以我们先定义基类 INode：

// C++实现
class INode
{
public:
    const unsigned weight;    // 权重
    virtual ~INode() {}


protected:
    INode(unsigned weight) : weight(weight) {}
};

为了避免不必要的干扰，将 INode 的构造函数声明为 protected。

叶子节点与内部节点的定义即是继承 INode 后，把剩下的另外字段补充上去，通过调用父类 INode 的构造函数生成权值。

// 叶子节点
class LeafNode : public INode
{
public:
    const char c;    // 字符


    LeafNode(unsigned weight, char c) : INode(weight), c(c) {}
};

内部节点中指向左右子节点的链接毫无疑问使用指针来实现，且指向 INode 类型。自身权值则通过将左右子节点的权值相加得到。此外，还需显式声明一个析构函数，以便在后续操作中自动释放空间、防止野指针与内存泄漏。

// 内部节点
class InternalNode : public INode
{
public:
    INode * const left;    // 左指针
    INode * const right;    // 右指针


    InternalNode(INode * leftChild, INode * rightChild) : INode(leftChild->weight + rightChild->weight), left(leftChild), right(rightChild) {}
    ~InternalNode()
    {
        delete left;
        delete right;
    }
};

基本元素现已齐全，继续进行下一步操作。上一小节我们说到，静态 Huffman 算法需要对数据进行两次遍历，第一次是得到概率表并构建树，第二次才进行字符编码。先来看第一次，在构建树之前必须提供一套排好序的概率表，假设现在有这样一串字符DATACOMPRESSION，我们如何在计算机中用复杂度较低的算法统计并排序？肯定不能用眼睛盯着来数了。

因为总字符数是一定的，所以用字符出现的次数，即频数，来代替概率是等效的。统计频数很简单 —— 声明一个容量足够保存任意字符的数组，将遍历到的每个字符作为参数传递给这个数组，由于字符在现代计算机中均以 ASCII、Unicode 等编码集存储，所以每当遇到一个字符时就在数组中对应字符编码数值的位置递增 1 即可，省去了记录下标的麻烦。

// 生成频数表
#define CAPACITY 1<char * ptr = "DATACOMPRESSION";    // 声明字符串DATACOMPRESSION
unsigned frequencies[CAPACITY] = {0};    // 声明并初始化数组
while (*ptr != '')            // 依次在每个字符对应于数组的位置中递增1
    ++frequencies[*ptr++];

经过一番操作后，得到的数组状态如下，下标反映指针所指位置：

尽管浪费了很多未被填充的空间，但这点数量级的浪费实际上微不足道，况且填充的数据越多利用率也越高。

接下来，采用优先级队列 priority_queue 数据结构来构建二叉树是不二选择，既满足存储节点序列，又可自动排序，如此，事先也就不用再给频数表排序了。现在，封装函数 BuildTree，只需唯一形参 frequencies[CAPACITY]：

// 构建二叉树
INode* BuildTree(const unsigned (&frequencies)[CAPACITY])
{
    struct NodeCmp    // 声明仿函数用于priority_queue排序
    {
        bool operator()(const INode * lhs, const INode * rhs) const { return lhs->weight > rhs->weight; }
    };
    priority_queue, NodeCmp> tree;    // 得到对象tree*,>


    for (unsigned i = 0; i < CAPACITY; ++i)    // 构造叶子节点，返回地址到tree并排序
        if (frequencies[i] != 0)
            tree.push(new LeafNode(frequencies[i], static_cast(i)));


    while (tree.size() > 1)    // 不断向上构造内部节点，直至tree中只剩树根
    {
        INode * leftChild = tree.top();
        tree.pop();


        INode * rightChild = tree.top();
        tree.pop();


        INode * parent = new InternalNode(leftChild, rightChild);
        tree.push(parent);
    }
    return tree.top();
}

得到 priority_queue 的实例 tree 之后，便可开始遍历频数表，将权值不为 0 的字符连同权值一起以叶子节点类型对象存进 tree，并会按权值递增的顺序排列。完毕后，循环依次取出队头前两个最小的叶子节点记录地址，生成上层内部节点再入队重新排序，最终返回树根地址。

一切就绪，终于可以给字符编码了！字符编码两要素 —— 字符与码，一一对应，符合映射关系，用 vector 序列容器存储码、map 关联容器存储键值当是再好不过了。仍用一个函数实现此功能，需要三个参数：根节点地址、目的编码、map 容器。在函数体中，借助 dynamic_cast 类型识别符判断节点类型从而执行不同语句。若为内部节点，则在每层通过之前构建的二叉树指针划分为两路，左路添 0 ，右路添 1，再分别递归调用本身而进到下一层迭代；若为叶子节点，则说明已经到达我们要编码的字符处，于是插入<字符, 编码>键值对到 map 中。

// 搜索二叉树并编码
using HuffCode = vector;
using HuffCodeMap = map;,>


void GenerateCodes(const INode * node, const HuffCode& prefix, HuffCodeMap& outCodes)
{
    if (const InternalNode * in = dynamic_cast(node))    // 验证是否为内部节点
    {
        // 划分左路
        HuffCode leftPrefix = prefix;
        leftPrefix.push_back(false);
        GenerateCodes(in->left, leftPrefix, outCodes);
        // 划分右路
        HuffCode rightPrefix = prefix;
        rightPrefix.push_back(true);
        GenerateCodes(in->right, rightPrefix, outCodes);
    }
    else if (const LeafNode * lf = dynamic_cast(node))    // 验证是否为叶子节点
        outCodes[lf->c] = prefix;    // 插入键值对
}

至此，编码的整体流程我们已经基本实现了，接下来应对其进行测试、验证结果，用例如下：

#include 
#include 
#include 
#include 
#include 
#include
#include 
#include 
#include 


#define CAPACITY 1<using namespace std;
using HuffCode = vector;
using HuffCodeMap = map;,>


class INode
{
public:
    const unsigned weight;
    virtual ~INode() {}


protected:
    INode(unsigned weight) : weight(weight) {}
};


class InternalNode : public INode
{
public:
    INode * const left;
    INode * const right;


    InternalNode(INode * leftChild, INode * rightChild) : INode(leftChild->weight + rightChild->weight), left(leftChild), right(rightChild) {}
    ~InternalNode()
    {
        delete left;
        delete right;
    }
};


class LeafNode : public INode
{
public:
    const char c;


    LeafNode(unsigned weight, char c) : INode(weight), c(c) {}
};


// 构建树
INode* BuildTree(const unsigned (&frequencies)[CAPACITY])
{
    struct NodeCmp
    {
        bool operator()(const INode * lhs, const INode * rhs) const { return lhs->weight > rhs->weight; }
    };
    priority_queue, NodeCmp> tree;*,>


    for (unsigned i = 0; i < CAPACITY; ++i)
        if (frequencies[i] != 0)
            tree.push(new LeafNode(frequencies[i], static_cast(i)));


    while (tree.size() > 1)
    {
        INode * leftChild = tree.top();
        tree.pop();


        INode * rightChild = tree.top();
        tree.pop();


        INode * parent = new InternalNode(leftChild, rightChild);
        tree.push(parent);
    }
    return tree.top();
}


// 搜索二叉树并编码
void GenerateCodes(const INode * node, const HuffCode& prefix, HuffCodeMap& outCodes)
{
    if (const InternalNode * in = dynamic_cast(node))
    {
        HuffCode leftPrefix = prefix;
        leftPrefix.push_back(false);
        GenerateCodes(in->left, leftPrefix, outCodes);


        HuffCode rightPrefix = prefix;
        rightPrefix.push_back(true);
        GenerateCodes(in->right, rightPrefix, outCodes);
    }
    else if (const LeafNode * lf = dynamic_cast(node))
        outCodes[lf->c] = prefix;
}


int main()
{
    char* SampleString = nullptr;    // 声明指向字符数组的指针
    cout << "Input original string: ";


    // 判定堆内存分配成功与否及读取输入行
    while ((SampleString = new char[CAPACITY]) && cin.getline(SampleString, CAPACITY))
    {
        // 编码过程
        cout << endl;
        char * ptr = SampleString;    // 创建地址副本
        unsigned frequencies[CAPACITY] = {0};    // 初始化频率表
        while (*ptr != '')    // 统计频次
            ++frequencies[*ptr++];


        INode * root = BuildTree(frequencies);    // 得到对应哈夫曼树并返回根节点地址
        HuffCodeMap codes;
        GenerateCodes(root, HuffCode(), codes);    // 为每个字符赋予哈夫曼码
        delete root;


        // 遍历map容器输出不同字符与编码
        for (HuffCodeMap::const_iterator it = codes.begin(); it != codes.end(); ++it)
        {
            cout << it->first << ": ";
            copy(it->second.begin(), it->second.end(), ostream_iterator(cout));
            cout << endl;
        }
        cout << SampleString << ": ";
        ptr = SampleString;


        // 输出字符串完整编码
        while (*ptr != '')
        {
            for (HuffCodeMap::const_iterator it = codes.begin(); it != codes.end(); ++it)
                if (it->first == *ptr)
                    copy(it->second.begin(), it->second.end(), ostream_iterator(cout));
            ptr++;
        }
        delete SampleString;
        SampleString = nullptr;


        // 解码过程
        char choice;
        cout << endl << endl << "Decoding? (Y/N): ";
        cin.get(choice);
        // 判定是否继续
        if (toupper(choice) == 'Y')
        {
            char each;    // 定义单字符
            bool flag = true;
            HuffCode total;    // 定义bool向量
            HuffCodeMap::const_iterator it = codes.begin();    // 创建初始迭代器


            while (getchar() != '
')
                continue;
            cout << "Input encoded string: ";
            // 获取输入行单个字符
            while ((each = cin.get()) && each != '
')
            {
                each -= 48;    // 转换为数字表示
                total.push_back(static_cast(each));    // 强转为bool型压入容器
                // 依据编码表反向匹配
                while (it != codes.end())
                {
                    if (total == it->second)
                    {
                        if (flag)
                        {
                            cout << "Original string: ";
                            flag = false;
                        }
                        cout << it->first;    // 反向输出字符
                        total.clear();    // 清空容器
                    }
                    ++it;
                }
                it = codes.begin();
            }
        }
        else
            while (getchar() != '
')
                continue;
        cout << endl << string(60, '-') << endl << "Carry on, input next string: ";
    }
    cout << endl;


    return 0;
}<>

初始时，声明一个指向字符数组的指针用于保存字符串，然后从堆中创建一块 CAPACITY 大小的空间并获取用户输入。编码时，需要注意的点是声明频率表时应同时初始化为 0，避免最终频次统计错误。输出单个字符编码时，通过相应迭代器从头至尾遍历输出每对键、值。若输出完整编码，将每个字符进行一次比较匹配即可。解码时，用户输入的字符串为 01 长序列，因而定义单字符以方便逐位比较。每读取一位字符在 HuffCode 中尝试一轮全匹配，成功即输出，否则即进入下一轮迭代。

5.6动态哈夫曼码的设计

在此之前，我们一直所述的对象均为静态哈夫曼编码，静态哈夫曼码有个不太好的点，你差不多注意到了 —— 传统静态 Huffman 编码需要对数据进行两次遍历：第一次是构造和传输 Huffman 树到接收端，以收集消息中不同字符出现的频率计数；第二次再基于第一次构造的静态树结构，编码和传输消息本身。那么，这会导致在将其用于网络通信时产生较大延迟，或者在文件压缩应用程序中产生额外的磁盘访问进而减慢算法。

于是，动态哈夫曼编码诞生了。动态哈夫曼编码（Dynamic Huffman coding），又称适应性哈夫曼编码（Adaptive Huffman coding），是基于哈夫曼编码的自适应编码技术。它允许在符号正在传输时构建代码，允许一次编码并适应数据中变化的条件，即随着数据流的到达，动态地收集和更新符号的概率（频率）。一次编码的好处是使得源程序可以实时编码，但由于单个丢失会损坏整个代码，因此它对传输错误更加敏感。

所以，Faller 和 Gallager 两人各提出了一种单次遍历方案，后被 Knuth 大大改进，用于构造动态 Huffman 编码。发送器用来编码消息中第 t+1 个字符的二叉树（同时也是接收器用来重建第 t+1 个字符的二叉树）是消息前 t 个字符的二叉树。如此，发送器和接收器就都会从相同的初始树开始，发送器永远不需要将树发送给接收器。很显然，这与静态 Huffman 算法的情况不同。

不久，又有研究者设计并证明了一种于所有单遍方案中，在最坏情况下表现仍然是最优的算法 A，它可以用于网络通信的通用编码方案，也可以作为基于文字的压缩算法中的一种高效子例程。

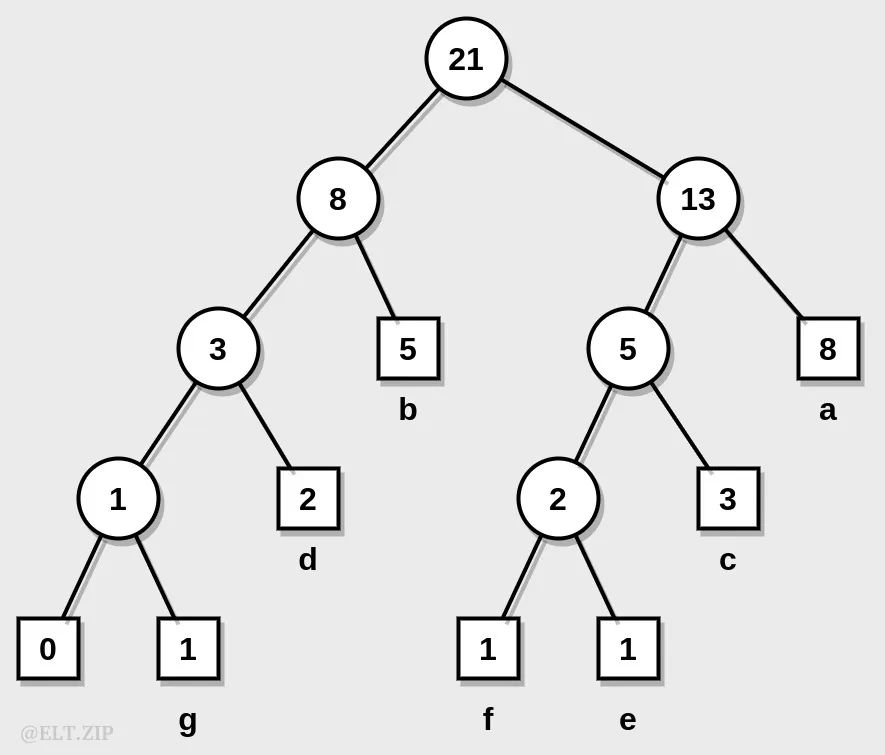
算法 A 具备以下优点：

对于编码效率差异相对较大的小消息，每个字母占用更少的位
在 t 小于 104 时，相比所有“两遍算法”都表现得更好
能对消息进行实时编解码，每个字符使用不到一个额外的比特位对消息编码
在文件压缩、网络通信和硬件实现方面有巨大应用潜力
可用来增强其他压缩方案

< 未完待续……>

ELT.ZIP是谁？

ELT<=>Elite(精英)，.ZIP为压缩格式，ELT.ZIP即压缩精英。

成员：

上海工程技术大学大二在校生闫旭

合肥师范学院大二在校生楚一凡

清华大学大二在校生赵宏博

成都信息工程大学大一在校生高云帆

黑龙江大学大一在校生高鸿萱

山东大学大三在校生张智腾

ELT.ZIP是来自6个地方的同学，在OpenHarmony成长计划啃论文俱乐部里，与来自华为、软通动力、润和软件、拓维信息、深开鸿等公司的高手一起，学习、研究、切磋操作系统技术...

写在最后

OpenHarmony 成长计划—“啃论文俱乐部”（以下简称“啃论文俱乐部”）是在 2022年 1 月 11 日的一次日常活动中诞生的。截至 3 月 31 日，啃论文俱乐部已有 87 名师生和企业导师参与，目前共有十二个技术方向并行探索，每个方向都有专业的技术老师带领同学们通过啃综述论文制定技术地图，按“降龙十八掌”的学习方法编排技术开发内容，并通过专业推广培养高校开发者成为软件技术学术级人才。

啃论文俱乐部的宗旨是希望同学们在开源活动中得到软件技术能力提升、得到技术写作能力提升、得到讲解技术能力提升。大学一年级新生〇门槛参与，已有俱乐部来自多所高校的大一同学写出高居榜首的技术文章。

如今，搜索“啃论文”，人们不禁想到、而且看到的都是我们——OpenHarmony 成长计划—“啃论文俱乐部”的产出。