上次我们分享了 Tustin变换法(双线性变换法) ,今天我们分享实际研发中非常常用的另一种变换方法:Fowler变换法(一阶后向差分法)
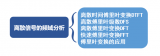
我们开始举例,已知连续校正环节传递函数D(s)为:
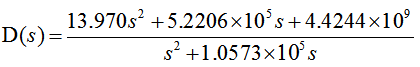
其中变换器的开关频率为fs=250kHz。如何设计双线性变换法所得的离散控制器D(z),并比较D(s)与D(z)的频率特性呢?
1)先利用matlab把D(s)离散成D(z):
① Fowler变换法(一阶后向差分法):
fs=250000;
T=1/fs;
Ds=tf([13.970 5.2206e5 4.4244e9],[1 1.0573e5 0]);
Dz=c2d(Ds,T,'fowler')
Transfer function:
12.31 z^2 - 22.86 z + 10.61
z^2 - 1.655 z + 0.6551
Sampling time: 4e-006
2)利用matlab绘制离散控制器D(z)的频率特性,代码如下:
T=4e-6;
w=0:1:4*pi/T;
f=w/2/pi;
num_d_s=[13.970 5.2206e5 4.4244e9];
den_d_s=[1 1.0753 0];
num_d_z=[12.31 -22.86 10.61];
den_d_z=[1 -1.655 0.6551];
[m_d_s,p_d_s]=bode(num_d_s,den_d_s,w);
[m_d_s,p_d_s]=bode(num_d_s,den_d_s,w);
[m_d_z,p_d_z]=dbode(num_d_z,den_d_z,T,w);
subplot(2,1,2),plot(f,p_d_s,'-',f,p_d_z,'-');
xlabel('Frequency(Hz)'),ylabel('phase(deg)');
axis([0 2/T -100 100]);
grid on;
subplot(2,1,1),plot(f,20log10(m_d_s),'-',f,20log10(m_d_z),'-'),title('BodeDiagrams');
xlabel('Frequency(Hz)'),ylabel('Magnitude(dB)');
axis([0 2/T 0 40]);
grid on;
3)连续控制器D(s)与离散控制器D(z)的频率特性如下图1:

图1 仿真图
以上就是**Fowler变换法(一阶后向差分法)**的简单过程,简单的3个步骤,即可以得到连续域与离散域的仿真图,是不是很简单呢?
-
matlab
+关注
关注
185文章
2979浏览量
230645 -
控制器
+关注
关注
112文章
16397浏览量
178514 -
数字电源
+关注
关注
28文章
515浏览量
109330
发布评论请先 登录
相关推荐




 数字电源中如何把连续频域变换为离散域(二)
数字电源中如何把连续频域变换为离散域(二)
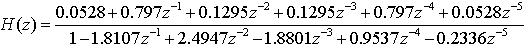










评论