一. 前言
你好,欢迎你打开这篇文章,这是我的系列立体匹配算法介绍文章中承上启下的一篇,请看看我们现在走到了哪一步:
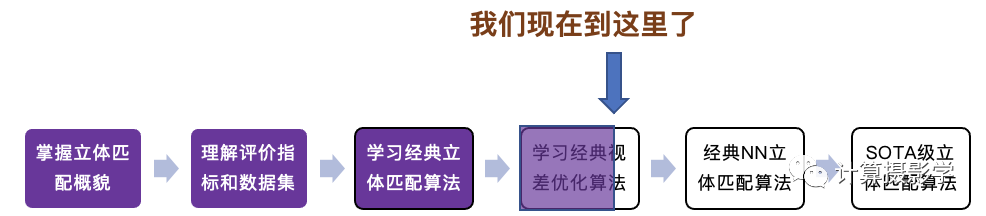
当前进度 今天,我将通过这一篇文章,填满上图箭头指向的格子! 下面我展示了一对双目相机拍摄的原始图像,已经过了立体校正:

一对做过立体校正后的双目图像 而下面左图是OpenCV的SGBM算法得到的视差图,右边则是通过我今天要介绍的算法处理后的视差图。看了它们后,我想你应该对什么叫做”化腐朽为神奇“有了深刻印象了吧。

左:SGBM算法结果 右:今日介绍的算法结果 那么如此神奇的效果,是如何做到的呢? 在复杂的问题进行空间转换,变换为小规模的易解问题的思想:
化简问题的思路 今天我介绍的这篇文章,也是基于这种思想的——事实上这就是同一个作者Jon Barron,基于相同思想的进一步研究,

Jon Barron文章介绍 这个算法我在后文中会简称为FBS,它是我在立体匹配的研究和工程应用中最喜欢的算法之一。这个算法相比我之前介绍的Fast Bilateral-Space Stereo有什么不同呢? 上一篇文章所讲的Fast Bilateral-Space Stereo,解决的是立体匹配问题——它将立体匹配当成下面的全局匹配代价最小化问题进行解决。

Fast Bilateral-Space Stereo算法思想总结 这个算法的优点我们已经讲过了,在此不再赘述。然而它也有明显的缺点。 首先是其匹配代价函数过于简单,上面公式中第二项是就是匹配代价项,也即是数据项。为了尽可能简单快速求解,作者采用了下面这样非常简单的形式:
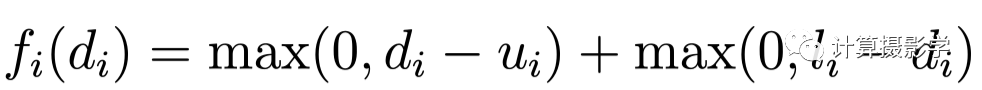
简化的立体匹配代价函数 图示如下:
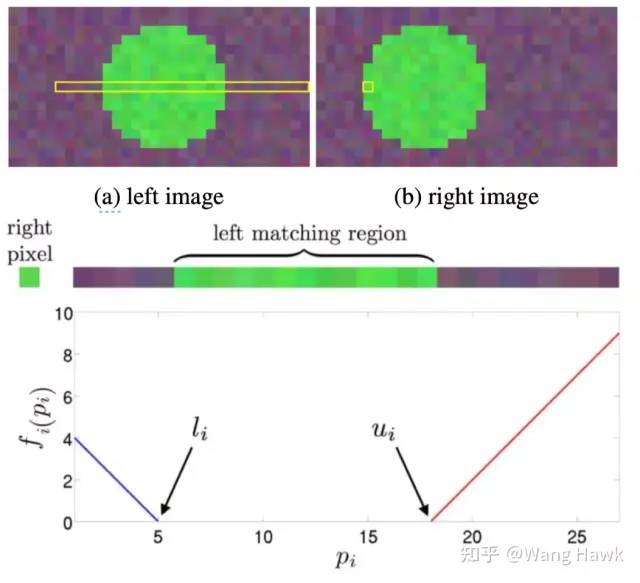
图示这种简化问题的思路 然而,正是因为其形式非常简单,因此效果也不够好,很容易出现大大小小的错误。 Fast Bilateral-Space Stereo算法的另外一个问题是,作者把上述代价映射到了双边空间,用一种叫做L-BFGS的方法进行求解,这是Broyden,Fletcher,Goldfarb,Shanno这几位数学家发明的优化算法,他们名字的首字母组合就是BFGS。这是一种迭代式的求解方法,它的求解速度是比较慢的。
同时,Fast Bilateral-Space Stereo的求解方法也无法应用到深度学习过程中,因为其代价函数也无法求导进行反向传播。这一点我之后再谈。 今天要讲的FBS,则采用了特别不一样的思想,如下图所示。Fast Bilateral-Space Stereo的一大缺点就是采用了较低质量的匹配函数,所以Fast Bilateral Solver(即所谓FBS)干脆不自己做匹配,而是允许其他算法算出一个初始的还不够好的视差图,然后再通过最优化一个全局代价函数来优化这个初始的视差图,最终得到一个更好的结果:
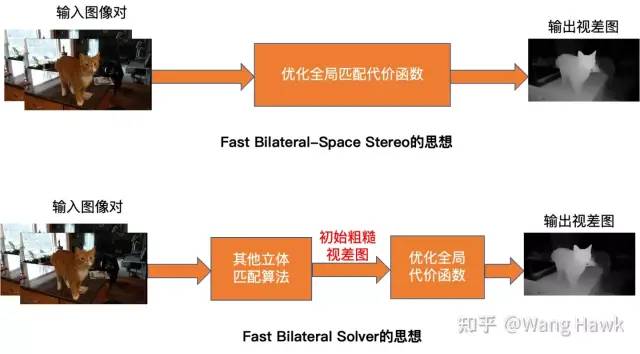
FBS思想 在作者论文中开篇就用下面这幅图来说明了这个思想:

利用FBS优化视差图 我一开始给大家呈现的关于猫猫的视差图(下面右图),就是用FBS处理了SGBM算法的结果(左图)后得到的,这也是我最喜欢的FBS的用法:

左:SGBM算法结果 右:FBS优化左图的结果 FBS的优秀之处在于它不仅仅可以用于优化初始的视差图,还能做得更多,比如视差图或深度图图的超分辨率重建。这里有一个低质量的输入视差图y,以及一个参考图像R,通过FBS可以得到高质量的输出图像x,其中x相对于参考图像R满足双边平滑的特性,且其边缘贴合参考图像的边缘,同时x还与输入图像y尽可能相似。
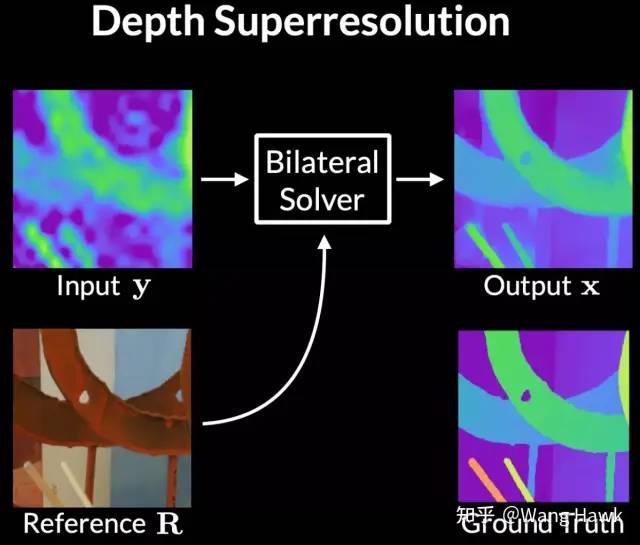
在图像超分钟应用FBS 另外一个有趣的应用是用户引导的灰度图像上色。这里也有低质量的输入图像y,即用户指定的最终色彩图像的骨架,原始的灰度图像则作为参考图像。再指定一个置信度图c,我们一样通过FBS求解输出彩色图像x,并且要求x自身相对参考图像来说是双边平滑的,同时还在高置信度的区域和用户输入y尽可能一致。
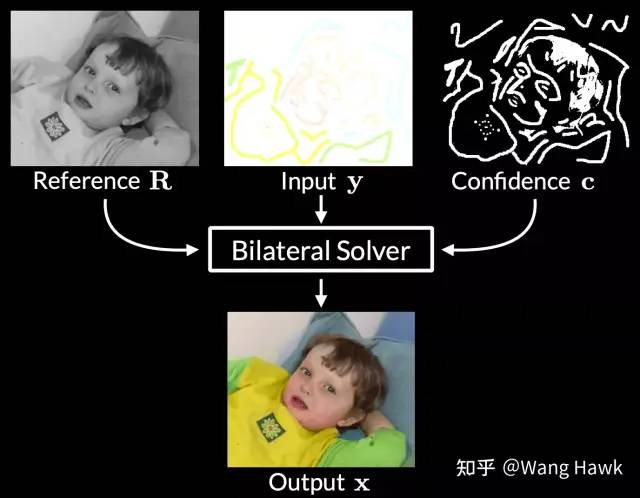
在图像上色中应用FBS 看出来了吧?FBS算法可以用于优化任意的输入图像,只要给出了一个参考图像和一个目标图像,它就会努力的让输出图像既能够按照参考图像来双边平滑,又能够非常接近目标图像,所以这是一种非常通用的算法。那么在下一节中,我们从原理上理解一下FBS算法。
二. FBS算法的应用目标和原理
2.1 FBS算法要解决的问题
用数学公式更加严谨的说明一下FBS吧。我们的目标是求解一个未知的图像x,它本身相对于参考图像R是双边平滑的(下式第1项),但在高置信度的区域又是和输入的目标图像t又是非常接近的。

FBS试图优化的全局代价函数 刚才给过的这张图,清晰的展示了上面公式的4张图。左上图为目标图像t,是由一个立体匹配算法得到的初始视差图。而右上图是输出图x,是经过FBS优化得到的结果。左下图是置信度图c,右下图则是输入的参考图像R,上面公式中的W就是由输入参考图像R计算而来的。
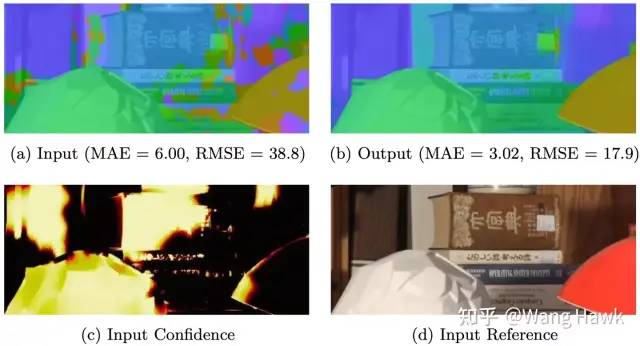
FBS应用到视差后处理优化的示例
2.2 将问题转换到双边空间
求解上述的最小化的问题非常复杂,于是我们沿用上一次讲到的思想,将问题转换到双边空间中去求解。不过,FBS和Fast Bilateral Stereo算法在双边空间中的表达式有关键的区别:

在双边空间中比较FBS及Fast Bilateral-Space算法 可以看到,FBS在双边空间中的求解非常简单,直接求解一个线性等式Ay=b即可,这是因为FBS不再需要承担做立体匹配的职责,它只需要保证优化后的视差图满足双边平滑以及与初始视差图尽可能相似即可。 当在双边空间中求得了y,接下来就再用下面的公式把结果转换为像素空间,就可以得到像素空间中的优化后的视差图了:

看起来是不是很简单?所以上面公式中最关键的就是要找出公式(6)中A和b及c的表达式,作者论文中已经给出:
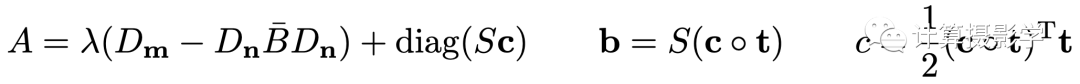
下面我们再解释一下上面几个公式中的各个变量:
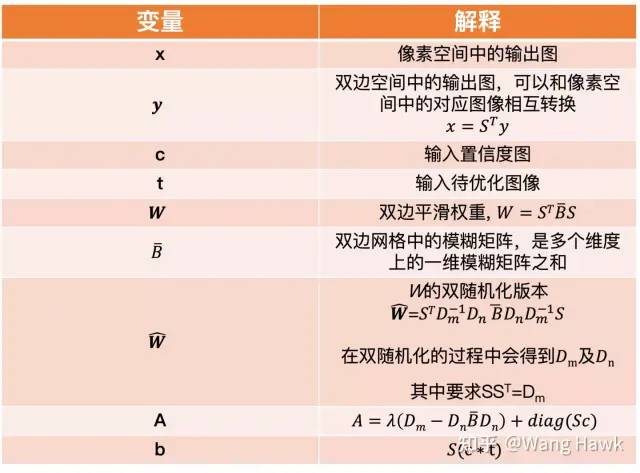
公式变量解释 当构造了上面提到的Ay = b这样的等式之后,作者采用了一种叫做preconditioned conjugate gradient (PCG)的算法(带先验条件的共轭梯度算法)来优化它,并且在这个过程中还采用了级联金字塔的思想。这个过程略去不表,咱们只需要知道,采用了这种方式之后,整个问题的构建和优化速度都比之前介绍的Fast Bilateral Stereo大大加快了:
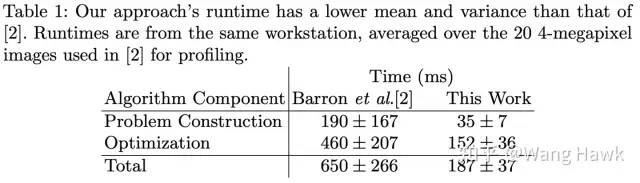
FBS的优化速度大大提升 在应用到对初始视差图进行优化的过程中,作者考虑到FBS的输出结果对于给定的置信度图和初始视差图比较敏感,还采用了一种迭代式的求解形式, 这个过程中的公式推导比较复杂,限于篇幅所限,这里我就略过了推导的过程。但作者给出了粗糙版的Python实现,在OpenCV里面也有相应的实现。我会在我的知识星球中,针对这两份代码做进一步的解释说明。
三. FBS的应用效果
让我先展示一些作者论文中的FBS的效果吧。首先我们看看一个当时最优秀的立体匹配算法MC-CNN的结果,这是第一代基于深度学习的立体匹配算法。下面是Middle Burry立体匹配数据集中的一幅图,从下图中看来,它在很多边缘细节上还是出现了错误和瑕疵:

MC-CNN算法结果 现在来看看经过FBS处理优化后的结果,我们看到从视觉上视差图结果明显好了一个档次,MAE和RMSE也有所降低,虽然bad 1%这个指标略有上涨。

用FBS优化MC-CNN算法结果大大减少了错误 下面是另外一张,很明显MC-CNN出现了很多瑕疵,尤其是近距离处出现很多匹配错误

下面是经过FBS优化后的结果,很明显视觉效果好了不少,MAE和RMSE也少了很多!

用FBS优化MC-CNN算法结果大大减少了错误
四. 可导性与深度学习
作者还花了不少篇幅来讲解将FBS作为一个“层”应用到深度学习的过程中,这里我也提一提吧。以语义分割为例,我们设想中将FBS作为网络的一个层加入到网络的输出部分,如下图所示,其目的是优化网络输出的分割掩模:

现在我们来看看现在比较常见的卷积神经网络优化损失函数的过程,下面是这个过程的图示:
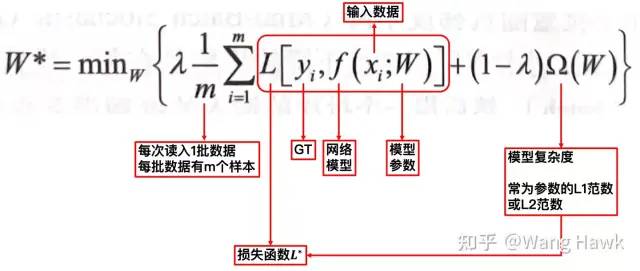
深度学习用于优化复杂的目标函数 直接优化上述函数是很困难的,所以实际中一般会采用小批量随机梯度下降法来求解
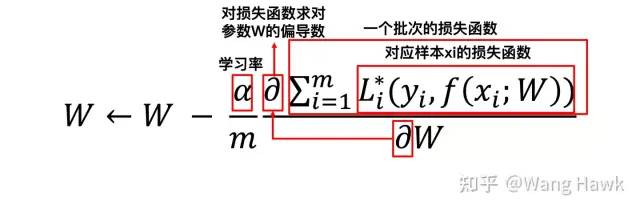
梯度下降法要求损失函数可导 所以这里很关键的就是损失函数要能够对各个待优化参数求偏导数,要在反向传播的过程中可导。如果我们把FBS作为网络的一个层,应用到网络构建的过程中,也会要求它可导。
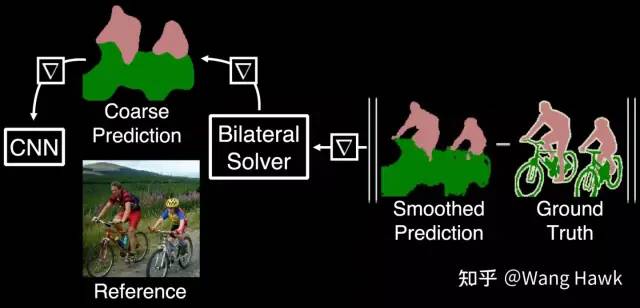
在反向传播中要求FBS可导 在FBS之前有很多全局能量优化的算法,都很难做到这一点。幸运的是,作者证明了FBS是可以用于反向传播的,我们把FBS看做下面这样的函数
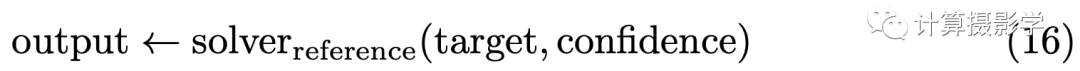
那么反向传播需要求解它对于输入的两幅图像的偏导数:
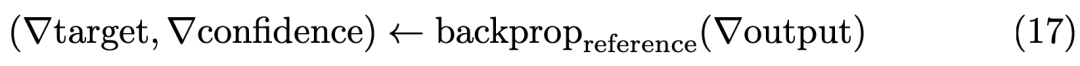
作者在论文中给出了两个偏导数的公式:
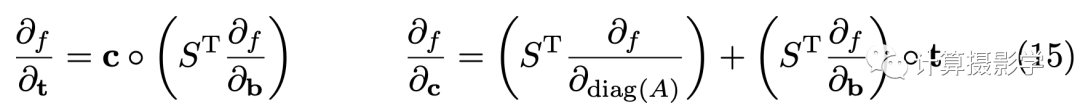
作者给了一个例子,来说明引入了FBS到网络中的好处,首先是用Deeplab进行分割后的粗糙结果:
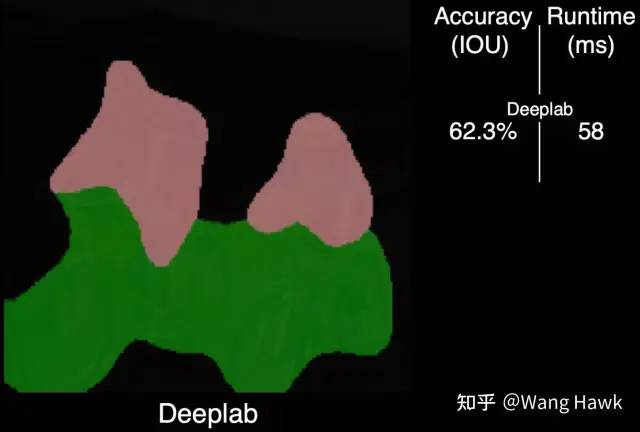
Deeplab语义分割结果 现在引入一个复杂的后处理算法DenseCRF, 可以得到下面的结果
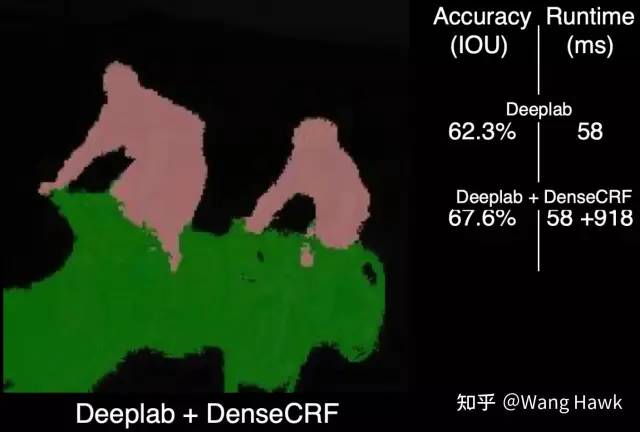
DenseCRF优化Deep Lab算法结果的展示 如果我们将DenseCRF替换为FBS加入到网络中,可以看到效果相似,但速度是11倍快!
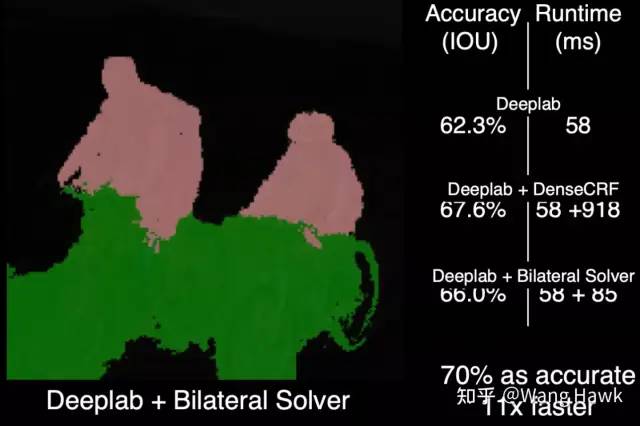
FBS优化Deep Lab算法结果的展示
五. 总结
今天我为你介绍了Jon Barron的经典算法Fast Bilateral Solver,可以说这是我最喜欢的算法之一。其中包含了很多深邃的思想。 首先是对很多问题中输出图像特性的敏锐观察,并把这种观察表达为了优美的数学公式。这种思想,和我之前在文章50. 从暗通道先验去雾到海底图像修复-三维重建辅助计算摄影中介绍的何凯明的“利用暗通道先验去雾”有异曲同工之妙。
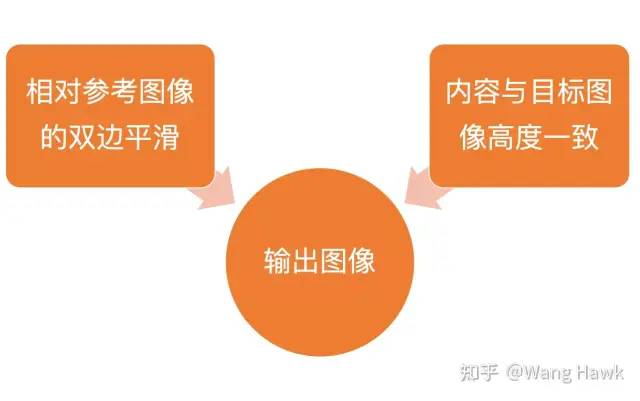
输出图像的两大特性 然后是作者将上述复杂的公式,转换到了双边空间中,降低问题规模,用于快速求解,而在今天所说的FBS算法中,作者又将这种思想进行了更深层次的应用。

问题转换求解空间 在求解问题的过程中,作者又高效的利用了级联金字塔形式,并采用了一种特殊的共轭梯度法来求解,使得求解过程大大加速,并得到了更好的效果。讲到这里不得不说作者的数学功底超级扎实,如果你看原文及作者的论文附件,一定会对文章中问题建立和问题优化的细致分析过程击节而叹!当然,读懂这些分析过程还是很烧脑的,所以我准备在我的知识星球中仔细的对应着作者的代码进行分析和注解,感兴趣的朋友可以加我“计算摄影学”公众号,进而了解星球的加入方法。 还有一点值得提的是, FBS在传统算法和深度学习算法中都可应用,可以说是连接过去和现在的桥梁,所以后面很多人写文章来描述如何将Fast Bilateral Solver的思想应用到深度学习算法中,感兴趣的话你可以搜索一下。

反向传播示例 不过,FBS也并非没有缺陷。它最大的问题也就在于双边平滑权重是与输入参考图像高度相关上——这使得其最终效果很容易受到输入参考图像的影响,很容易在结果中引入输入参考图像本身的纹理。下图中左下角是SGBM的结果,右下角是FBS处理后的结果。我们可以看到头发部分的视差图很明显引入了原图中美女头发部分的纹理特征,这并非我们想要的结果。处理这样的问题,需要我们在应用FBS的过程中,仔细的调整各个参数和输入的置信度图,并且选择性的应用FBS在部分区域上,而不是一股脑用于全图的所有像素上。

FBS容易引入参考图像的纹理信息 总的来说,FBS是一种非常经典和优秀的通用图像处理算法,当它应用到立体匹配的视差后处理时,能够起到“化腐朽为神奇”的功效,非常值得学习!现在看看我们的进度吧,我们终于完成了经典视差优化算法的学习,即将迈入立体匹配的现代算法——基于深度学习的立体匹配算法部分,惊不惊喜,期不期待 就让我们拭目以待吧!
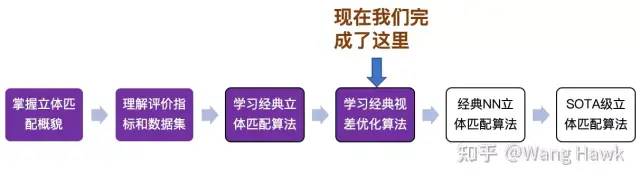
我们当前的进度
审核编辑 :李倩
-
算法
+关注
关注
23文章
4610浏览量
92859 -
函数
+关注
关注
3文章
4329浏览量
62588
原文标题:立体匹配:经典算法Fast Bilateral Solver
文章出处:【微信号:3D视觉工坊,微信公众号:3D视觉工坊】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
Celsius EC Solver:对电子系统散热性能进行准确快速分析
手写图像模板匹配算法在OpenCV中的实现

使用语义线索增强局部特征匹配

system_adc_read_fast为什么只能采集255个样本?
电路的阻抗如何匹配

机器学习的经典算法与应用

求助,为什么ble_mesh_fast_prov_server和ble_mesh_fast_prov_client运行之后没能连接上呢?
ble_mesh_fast_prov_client在配网时不能支持PB-GATT吗?
GPIO_MODE_OUT_OD_LOW_FAST和GPIO_MODE_OUT_OD_HIZ_FAST这两个是什么区别呢?
立体声放大器电路图分享
什么是匹配滤波器?如何理解匹配滤波器?
为什么要阻抗匹配?怎么进行阻抗匹配?




 立体匹配:经典算法Fast Bilateral Solver
立体匹配:经典算法Fast Bilateral Solver











评论