射频信号链的原位非线性校准

作者：Nevena Rakuljic, Carroll Speir, Eric Otte, Jeffery Bray, Corey Petersen, and Gabriele Manganaro

提出了一种线性化级联组合信号IC的新方法，用于原位校正PCB缺陷和相互加载。这样可以大幅缩短系统设计/原型设计周期，并以可忽略不计的功耗成本最大限度地提高信号链性能。报告了使用高达3GHz的RF信号并使用12b/10GSPS ADC进行的实验结果，验证了该方法的有效性。

介绍

基础设施通信系统、仪器仪表和防空应用的进步推动了对RF和混合信号IC的更高性能要求，特别是高速/高动态范围数据转换器[1-3]。

然而，在信号链中的IC之间插入的印刷电路板（PCB）和封装会引入寄生效应，并遭受制造缺陷的影响，从而导致网络中的电路不平衡并损害GHz信号的线性度。

模数转换器（ADC）的采样保持放大器（THA）前面通常有一个片内缓冲器，以简化与片外驱动放大器（或可变增益放大器）的耦合。片上缓冲能力有限，耗电大，并且在高频时会减弱。IC之间的相互加载引入了额外的非线性或改变IC最佳工作条件。

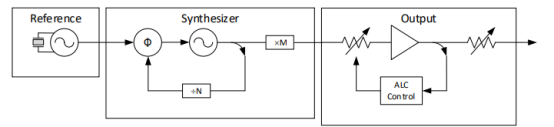
接收（Rx）信号链如图1所示。每个功能模块（混频器、驱动放大器、滤波器和ADC;后者包括前端缓冲器和THA）是同一PCB上的独立IC。虽然每个模块都可以单独（或在实验室的最佳定制板上）发挥最佳性能，但一旦耦合并受到杂散和实际PCB的限制，整个链的净性能可能会受到限制。

数字。1. 经典“接收”（Rx）信号链示例。

IC设计人员努力加强芯片接口的电路，以满足在各种负载条件下所需的性能。通常，使用这些组件的系统设计人员需要定制和迭代设计，以最大程度地减少上述损伤的影响。IC高级模型（通常是简单的电子表格）的局限性和电路板杂散建模不足加剧了这种努力。原型设计工作可能会为高性能系统的开发增加几个月的时间，并且需要IC供应商的应用工程人员的参与[4，5]。

这里介绍的非线性校准（NLC）方法通过在宽输入频率范围内校正动态非线性失真来缓解这些问题。RF/混合信号IC整个信号链的非线性模型的参数是原位确定的，即在系统板上确定。然后推导一个数字逆校正函数，使二阶和三阶失真为零。这是在信号链处理信号之前在前台执行的。然后，逆函数实时应用于ADC输出端的数据流，从而对损伤的影响进行后失真（线性化）。这让人想起数字预失真（DPD）或通信系统中的回声/传输消除[6]。

本文的组织结构如下。第二部分讨论校准系统及其操作。第三部分介绍了非线性、模型参数识别和二次和三次谐波失真的消除所采用的模型。最后，第四部分报告了实验结果，量化了所提出的校准的有效性。

信号链的非线性消除

背景

假设图1中的每个IC（例如驱动放大器、滤波器、ADC）都已经过单独优化。因此，例如，如果ADC需要内部前台校准[3]，则需要事先完成。

然后，我们考虑ADC数字输出之间存在的净静态非线性特性，例如，ADC的数字输出之间D外和驱动放大器的模拟输入v在如图 2 所示。图2的下部勾勒出卡通曲线（为了解释而夸大）。这捕获了由各种损伤引起的整体非线性，例如放大器和抗混叠滤波器之间以及滤波器和ADC输入之间携带差分模拟信号的成对走线之间的残余不平衡，加上所有杂散，以及模块之间的相互负载等。

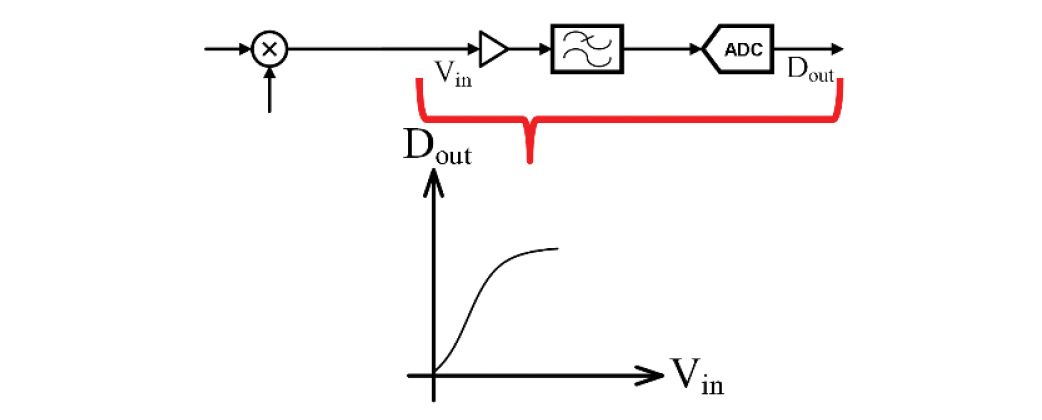
数字。2. 信号链非线性。

为了理解这一点，我们考虑一下，例如，仅ADC的低频线性度通常优于75dB，即优于5000分之一。无论ADC性能如何，任何电路板设计缺陷或随机制造缺陷，如果不是明显好于此缺陷，都会影响和降低信号链的净线性度。更糟糕的是，在处理GHz范围内的宽带信号的应用中，如基础设施通信系统或高性能仪器[6]，这种非线性也具有频率相关分量，因此其行为无法仅使用泰勒级数展开进行精确建模。

算法线性化的操作

假设信号路径非线性是弱单调非线性[6，7]。设 H（.） 是D外和v在如图2所示。所提出的消除方法包括通过应用反函数以数字方式反转其失真Hc(.)到ADC的输出数据流D外，返回线性化数据流D林如图 3 所示：

其中 G 和D0分别是转换增益和失调。Hc（.） 嵌入在 ADC 中，由表示转换器芯片的虚线表示。

数字。3. 非线性度的数字校正。反函数 Hc（.） 嵌入在 ADC 中（虚线勾勒出芯片）。

Hc(.)其特征在于由向量C捕获的许多模型参数。下面概述了原位确定C的程序。

为此，H（.） 需要使用施加的信号来执行。这是在信号链工作之前完成的，没有混频器输出。在驱动放大器的输入端生成并注入测试信号u。u由数模转换器（DAC）合成，该转换器也与ADC位于同一芯片上，如图4所示，但集成不是必需的。DAC线性度需要优于目标信号路径线性度。微控制器uC还嵌入在ADC中，以执行多种功能，包括ADC本身的初始校准[3]，此处用于控制和执行模型识别算法和反函数创建。

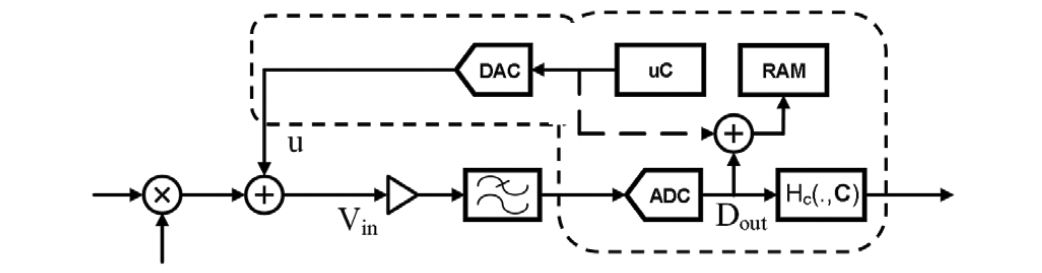
数字。4.注入测试信号。

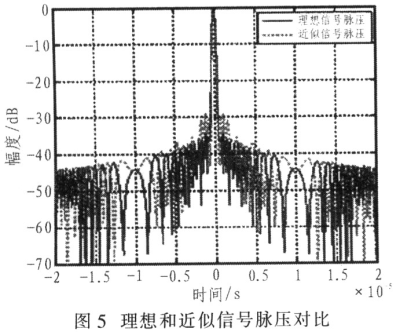
模数转换器输出D外对应于由H（.）处理的信号U的数字表示存储在片上RAM上。在此之后，u 归零，RAM 的内容由 uC 处理以估计 C，从而确定Hc（.，C） 如图 5 所示，稍后将对此进行详细说明。

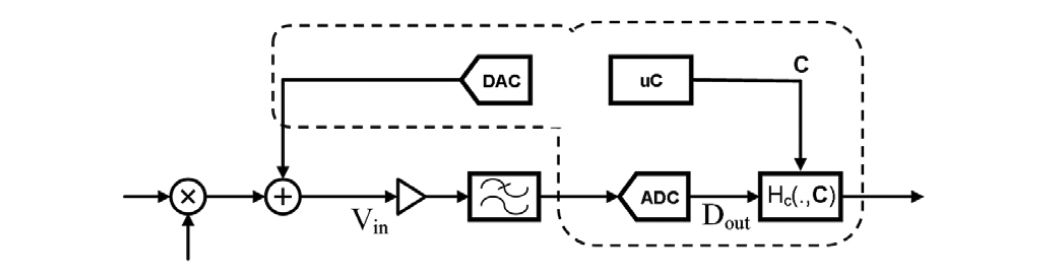
数字。5.校正参数的确定。

一旦找到C，信号链就可以以实际v在，现在是混频器的输出，并返回线性化输出D林（因为 Hc（.） 使链失真无效）。从这一点开始，C没有变化。如果工作温度或其他参数漂移重新出现过度失真，则需要重新校准[9]。

所提出的方法是可扩展到功能更多的块。例如，还可以包括驱动放大器前面的混频器。为此，用于注入u的求和节点在图5左侧的混频器信号输入处向上游移动。施加u时，另一个混频器的端口需要用本地振荡器激励，但在此校准阶段，没有其他RF信号施加到混频器的Rx输入。该过程在概念上与前面描述的过程相同。

建模、刺激和校正

建 模

H（.） 及其逆模型类型所采用的模型类型Hc(.)是一个平行的、时间离散的哈默斯坦模型[8]，由平行分支组成，每个分支包含一个静态非线性元素，后跟一个动态线性元素。这种选择是合理的，因为非线性的主要来源的性质是连续时间驱动放大器、滤波器、缓冲器等[6，7]。当其他非线性源（如时间交错失真或采样电荷注入失真）先前可以忽略不计时，这是有效的[1-3，9]。

图 5 链的完整动态模型如图 6 所示。所有具有传递函数 G 的模块都是线性滤波器。例如，理想的DAC输出u可以由传递函数线性频率塑造G发援会，通常可能与传递函数不同G我来自混频器的射频输出。H（.） 的模型由线性分量、二次分量和立方分量组成，每个分量都有线性滤波器。理想量化器Q返回数字输出D外频率采样fs.

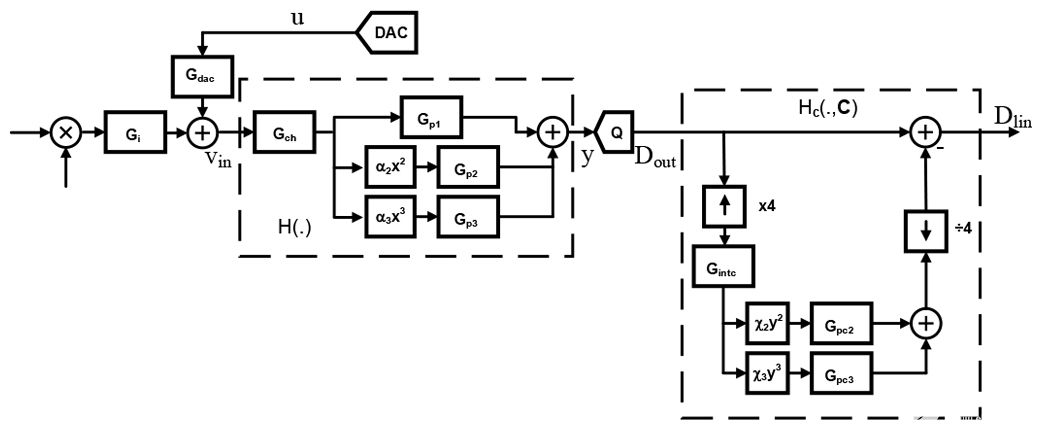
图6.链的完整模型，包括 H（.） 和 HC（.）。

D外然后由Hc（.，C），它也使用哈默斯坦模型，其中输入信号的二次分量和三次分量被估计、组合并从失真序列中减去D外返回更正的序列D林.Hc（.，C） 中的函数系数构成 C，这些系数可以直接与 H（.） 中的系数代数相关。

而v在假设始终处于第一奈奎斯特波段（输入频率f在假定为f在C 的训练算法中产生了歧义，并且还需要分别估计二次项和三次项的传递函数响应，并分别估计第二和第三奈奎斯特区。校正中的歧义已在 H 中得到解决C通过引入足够高的插值，在我们的例子中为 4x，在二次和三次校正项的求和之前（随后在应用校正之前被抽取 4）。

刺激和模型识别

DAC和ADC均以速率计时fs.宽带伪随机序列以及单音和双音都被用作刺激来训练系数C并导致可比较的结果，尽管这两种方法中的每一种都有自己的优点和缺点。在本文的其余部分，仅讨论了单音调刺激的情况。

在这种情况下，DAC 将 u 合成为形式为 cos（ωt + ɸ0).产生多个频率ω的音调，确保产生的谐波不会相互叠加混叠（即在采样时，这些谐波不会落在相同的频率箱中）。

使用比图 6 所示更简单的 H（.） 模型，为了简化数学运算，理想采样器/量化器 Q 之前的失真信号 y（t） 可以写为 y（t） = [α1v在（t） + α2v在2（t） + α3v在3（t）] *g3（t） 凡α2和α3是失真系数，非线性项与线性时不变（LT I）脉冲响应复杂g3更正D外的训练算法Hc需要估计α2, α3和g3（t）。

y 的傅里叶变换为：

其中 Г（ω） 包含一些其他（交叉）项，而不是ωo, 2ωo或 3ωo.这可以写成：

其中 ɸ（ω） 包含一些其他不在ωo, 2ωo或 3ωoα和β可以相互关联。因为D外是 Y 的数字表示，因此：

由H（.）产生的基波、二次和第一次谐波，标度和相移G3很容易看到。这些术语映射到Hc取消二次项和三次项。因此，C 可以从 H（.） 计算出来。反过来，H（.）可以从其通过以均匀间隔的频率注入音调u获得的频率响应中识别出来，如第II节所述，避免主谐波落在相同的FFT箱上。然后，如所见，C 是代数找到的。

（4）上的更多代数表明，当二阶和三阶谐波D外别名到第一奈奎斯特带，（4）中的相应项被相位否定，这需要跟踪。此外，而不是提取β2G3（eJωo), β3G3（eJ3Ωo）在（4）中，它们与β的关系1G3（eJωo）实际使用，因此仅在第一奈奎斯特区需要激励，但需要更多计算。如果G发援会是一个一阶系统，它的影响可以通过了解的力量来解释D外的根本。最后，将DAC定时于以下位置引入的另一个实际限制fs如f在接近奈奎斯特，是u将是sinc形的，更重要的是u的（fs–f在） 第一个图像也接近奈奎斯特并产生光谱估计问题。

实验结果

NLC已应用于信号链，如图2所示，并使用图7所示的芯片，嵌入[3]中所述的12b/10GSPS ADC、14b/10GSPS信号注入DAC、10GHz低相位噪声时钟合成器、校准引擎（包括微控制器uC）和本文范围之外的其他功能， 例如数字下变频器和滤波器。此处报告的结果是在采样率fs=6GSPS，这是射频信号接近3GHz的通信系统所要求的[6]。

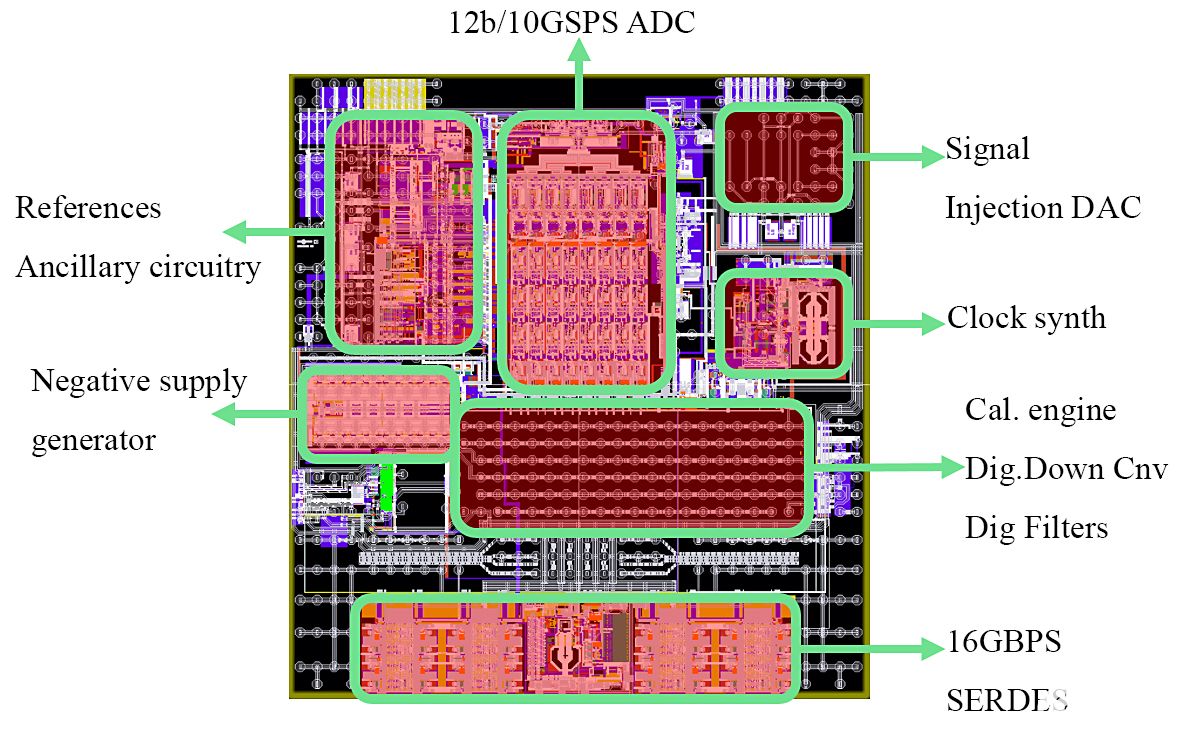
数字。7.芯片的芯片布局和主要功能块。

在对近满量程激励进行线性化之前，已经测量了信号链的单音次级（HD2）和三次谐波（HD3）失真性能、信噪比（SNR）、无杂散动态范围（SFDR）和双音三阶交调失真（IMD3）。结果在图8-11中标记为“标称”的曲线中报告。

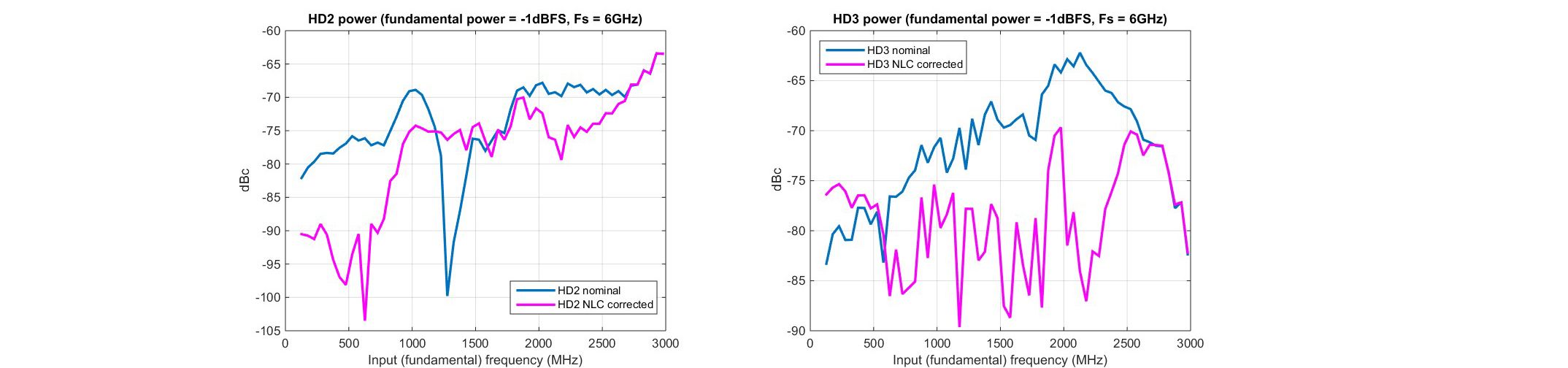
数字。8. （a） HD2 和 （b） HD3 与 f 的单音失真性能在线性化之前（标称）和线性化后（校正）的基波输入功率为 -1dBFS 和 fs=6GSPS。

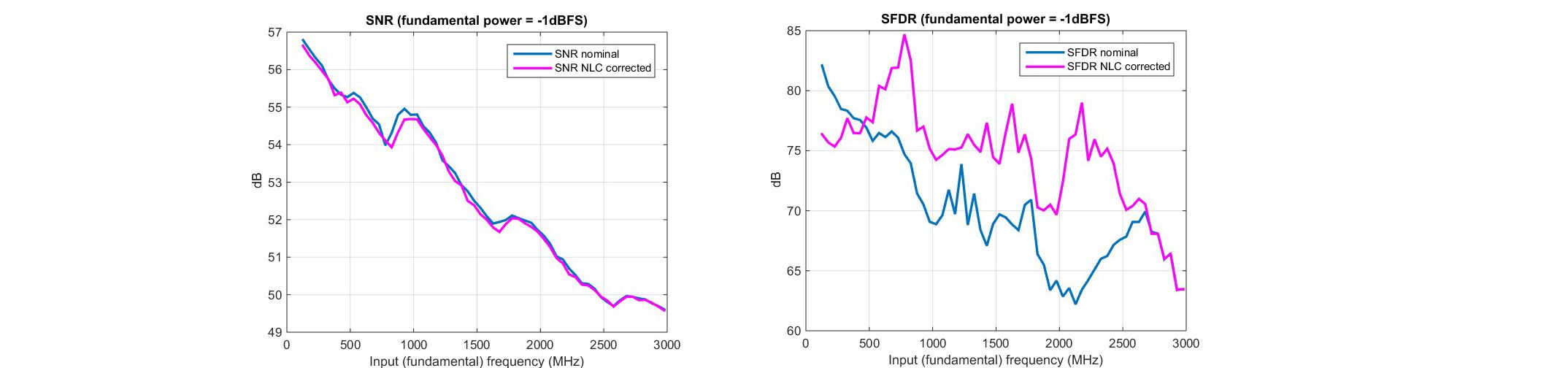
数字。9. （a） 信噪比和 （b） SFDR 与 f在对于 -1dBFS 和 f 的输入s=6GSPS。

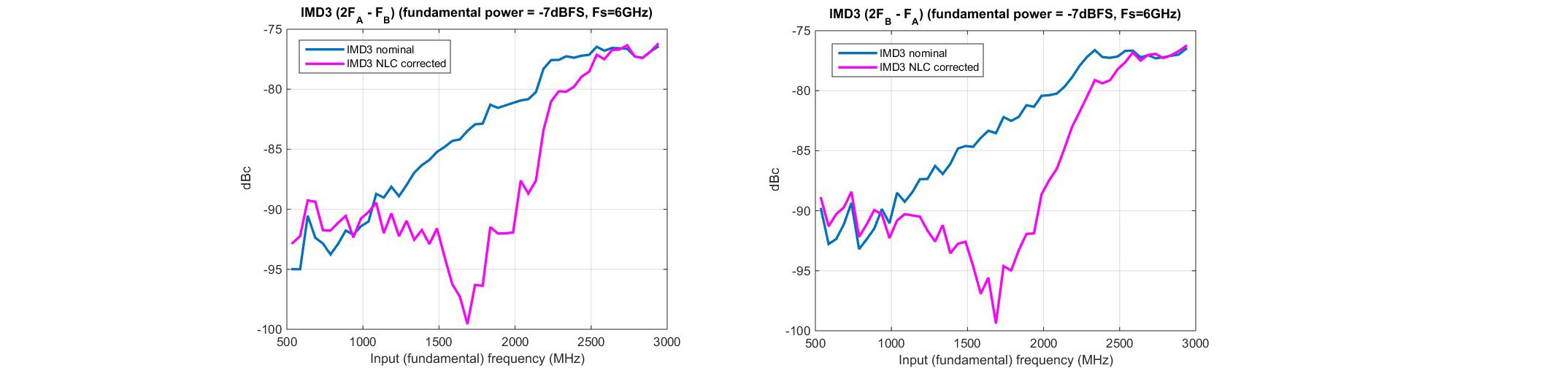
数字。10. 双音IMD3 for （a） （2F）一个–Fb） 及 （b） （2楼）b–F一个） 与 f在= （F一个+Fb）/2 表示 –7dBFS 和 f 的输入s=6GSPS。

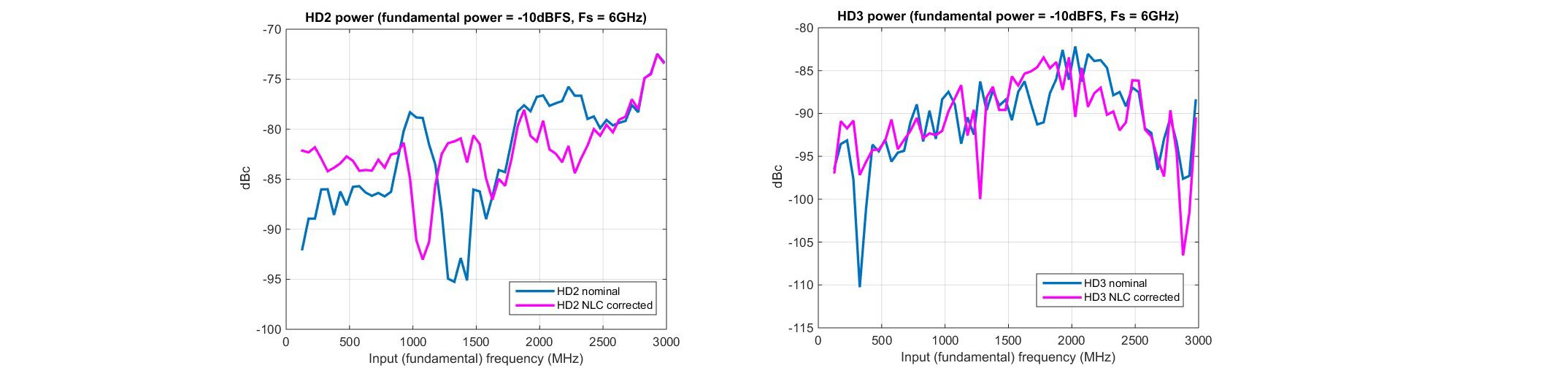
数字。11. （a） HD2 和 （b） HD3 与 f在适用于 –10dBFS 和 f 的小输入s= 6GSPS。

然后应用 NLC，再次测量性能指标，并在标记为“NLC 校正”的叠加曲线中以相同的数字报告。在NLC之后，线性度性能在几乎整个奈奎斯特范围内显著改善，最终随着输入接近而达到递减的回报fs/2，如预期的那样。图10a显示噪声性能（SNR）没有像预期的那样受到影响。图10b中SFDR的改进证实了HD2和HD3的主要贡献，验证了对模型选择所做的假设。

虽然这些曲线显示了接近满量程（-1dBFS）激励的系统性能，但重要的是要确认NLC适用于较小的激励。因此，无需重新校准，而只需减少v在的功率，失真已在较低的输入功率电平（即-3dBFS，-6dBFS，-10dBFS）下重新测量。由于空间限制，图11中仅报告了-10 dBFS的更极端情况。虽然由于激励较小，标称性能在前期有所改善，但除了低频时HD2略有下降外，NLC性能优于或与标称性能相当，证实了该方法的鲁棒性。

在实时运行的校准链中，数字逆函数的应用仅增加了约150mW的功耗，而整个信号链消耗的总功耗超过5W，无需校正。

审核编辑：郭婷