本文将向大家介绍一种在科学研究中非常重要和有趣的计算方法——蒙特卡洛方法,这种方法在数学、物理学、化学、工程、经济学、环境动力学等多个领域都有广泛的应用。
到底什么是蒙特卡洛方法?我们可以先从它的名字开始了解,蒙特卡洛(Monte Carlo)是摩纳哥公国的一座城市,是世界著名的“赌城”。以“蒙特卡洛”来命名这种计算方法就是因为其本身便是一种概率算法,其核心思路是通过概率实验所求的概率来计算我们感兴趣的一个量。
概率算法的1.0版
为了更好地理解蒙特卡洛方法,我们先简单了解一下“蒲丰投针问题”,这个问题的提出被认为是蒙特卡洛方法的起源。 18世纪,法国数学家蒲丰提出了一种计算圆周率π的方法——随机投针法:假设我们有一个以平行且等距为a的木纹铺成的地板,随意抛一支长度为l(比木纹之间距离小)的针,通过针和其中一条木纹相交的概率p,即可计算圆周率π。计算公式为:
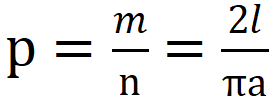
,其中n是投针的总次数,m是针与平行直线交点的总数目。

图 蒲丰投针问题示意图
这个方法的原理可以通过概率学的推导计算来进行证明。由于投针掉落的位置与方向都是随机且独立的。我们假定落地后针的中心距最近的地板条纹的距离为X,那么X在[0,a/2]上均匀分布;针与地板条纹的夹角为Y,则Y在[0, π/2]之间均匀分布。当
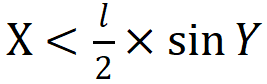
时,针与木纹相交,因此(X,Y)的概率密度函数和相交的概率P分别为:
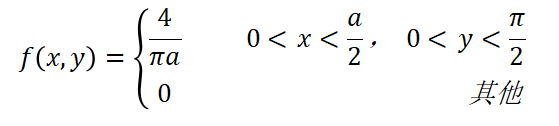
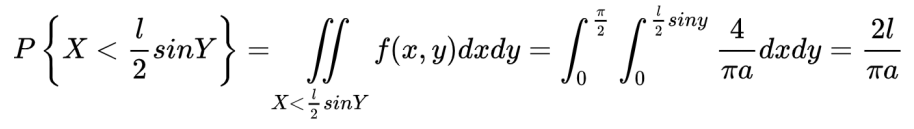
相信大家都听懂了,下面我们可以…… 好吧,这里还有一种虽然不够严谨、但易于理解的解释: 我们想象一个长度为πa的铁丝,被绕成了一个直径为a的圆环。那么无论我们怎么扔这个铁环,它与条纹的交点恒为两个,因此当投针n次后,相交的次数恒为2n。如果我们把铁丝拉直再扔,这样的铁丝扔下时与平行线相交的情形要比圆圈复杂些,可能有4个交点、3个交点、2个交点、1个交点,甚至于都不相交。由于圆圈和直杆的长度同为πa,根据机会均等的原理,投掷n次,直杆与平行线组交点的总数期望也是2n。同时还有一个规律,当投针次数n固定时,铁丝的长度l与交点总数m应为正比关系,即m=kl。考虑到l=πa时,m=2n,将
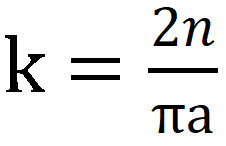
代入前式可得:
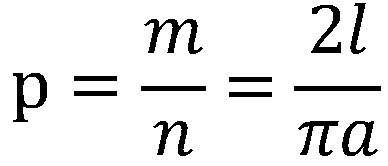
。 投针试验既然是依靠概率的算法,那么随着投针次数越来越多,计算求得的π值也会越来越接近于真实值。下表给出了一些比较出名的投针试验得到的圆周率估计值,可以看到在投掷数千次后,计算得到的圆周率与我们所熟知的π值的误差仍较大。
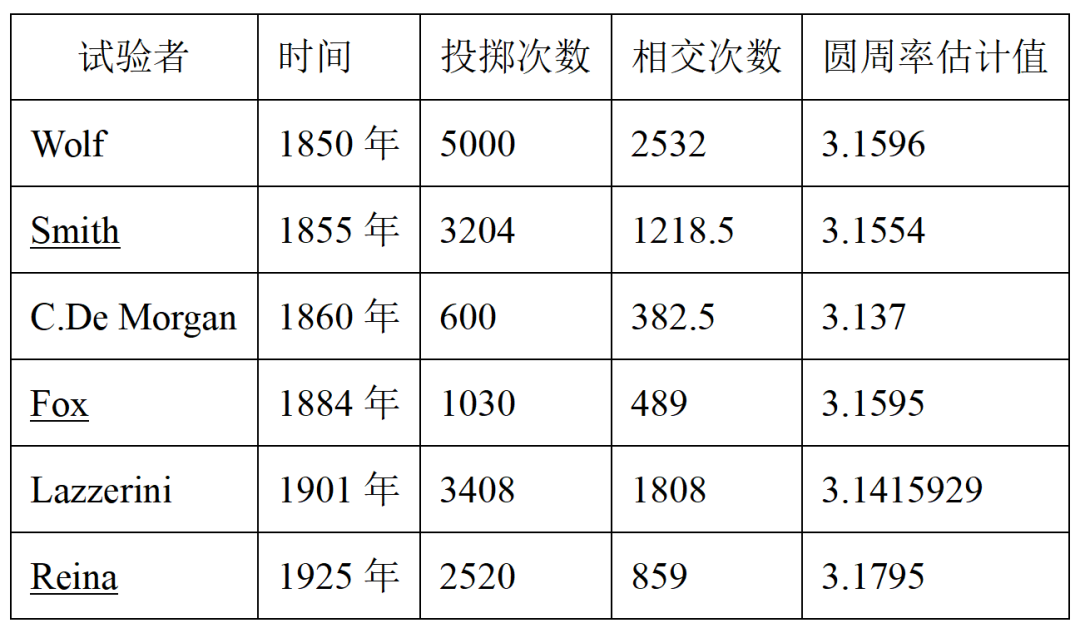
表 一些投针试验的计算结果
1995年,马修斯发表了他如何通过观察天空中亮星的分布计算圆周率。他的试验方法基于一个基本的原理:任意两个自然数互质的概率为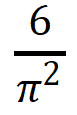 。他从众多星星中选择100个亮星,将这些亮星两个分成一对,然后计算每对星之间的角距,得出一堆数据,然后检查这些数据的因子情况,从中计算出π值约为3.12772。
。他从众多星星中选择100个亮星,将这些亮星两个分成一对,然后计算每对星之间的角距,得出一堆数据,然后检查这些数据的因子情况,从中计算出π值约为3.12772。
从上述两个例子来看,依靠重复的物理、观测等试验行为来获取随机性数据的方法往往很难得到令人满意的计算结果,这主要是受到了样本数量的限制。而早在魏晋时,我国的刘徽便通过割圆术求得了π的近似值3.1416。
“史诗级加强”X.0版
20世纪40年代,美国“曼哈顿计划”的成员S.M.乌拉姆和J·冯·诺伊曼第一次把这种通过概率事件来计算关注的确定值的方法命名为“蒙特卡洛方法”。随着电子计算机的发明和科学技术的发展,蒙特卡洛方法得到了“史诗级加强”。

图 S.M.乌拉姆(左)和J·冯·诺伊曼(右)
计算机在进行蒙特卡洛模拟的过程中获取随机性最根本的方法是通过固定算法得到符合[0,1]均匀分布的“伪随机数”,它并不真正的随机,但具有类似于随机数的统计特征,如均匀性、独立性等。
这里介绍另一种计算π值的蒙特卡洛方法——“撒豆法”。该方法假定有无数个豆子被均匀地撒在下图所示的正方形中,那么落在圆内的豆子数m与落在正方形内的豆子总数n的比值的期望应与它们面积的比值一致,即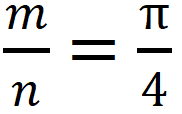 ,这样就可以计算得到π的值。
,这样就可以计算得到π的值。

图 “撒豆法”求解π值模型示意图
利用计算机开展上述计算,仅需不到一分钟的时间,便可以完成十亿次“撒豆”,并得到相应的计算结果。计算的python代码及运行结果见下图。
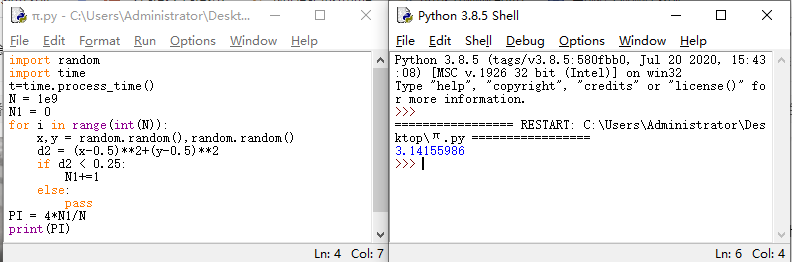
图 计算所用python代码及计算结果
计算机时代的蒙特卡洛模拟无疑具有超高的计算效率,且其计算效率随着计算机技术的飞速发展而不断提升。
核科学领域中的应用
蒙特卡洛方法在核科学领域中有着广泛的应用。核物理领域的基本参数(如反应截面、散射发射角度分布、能谱分布、衰变、衰减等)主要来自核物理实验及理论模型等,而蒙特卡洛模拟程序也在与核物理实验、理论模型等的相互参照、验证和迭代更新中不断发展至今。
如今在核物理领域有许多广泛使用的蒙特卡洛程序,如FLUKA、MCNP、PHITS、GEANT4等,这些蒙特卡洛程序对核物理学的发展至关重要,同时它们的运用过程也非常的有趣和巧妙。
具体以加速器辐射防护领域为例,粒子加速器产生的高速运动的微观粒子(一般每秒可达上亿个粒子)在与其他物质碰撞时,会通过核反应产生带电粒子、中子、γ射线等次级辐射,这些次级辐射又会继续与材料发生核反应,产生更多的次级辐射。如此周而复始,其反应过程非常复杂,无法通过人力模拟计算。而蒙特卡洛方法,正好能够解决这个难题。
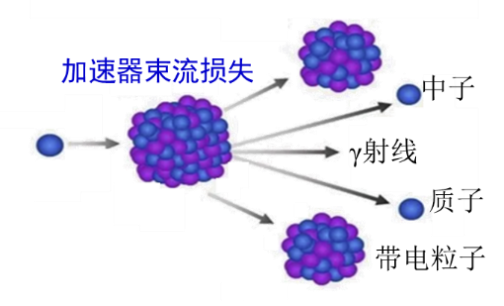
图 加速器产生电离辐射示意图
为了使加速器产生的强电离辐射降低到可接受的低水平,科研人员需要对次级粒子的输运过程进行仿真模拟,并根据模拟结果进行屏蔽阻挡设计。
接下来我们以一个简单模型为例,介绍蒙特卡洛方法应用于粒子输运模拟的基本思路。如下图所示,假定在一个二维的矩形屏蔽中,充满了物质B,左、上、下侧设置黑色隔板,右侧设置红色隔板。

图 模型示意图
假设粒子A具有以下特质:
粒子A在物质B中直线运动。但每直线前进1m,就会停止前进并与B发生反应,反应后继续直线前进。反应有三种可能:
①:A忽略与B的反应,继续按原方向前进1m,发生概率为1/3;
②:A与B发生正碰撞,向左偏转45°前进1m,发生概率为1/3;
③:A与B发生反碰撞,向右偏转45°前进1m,发生概率为1/3。
2. 当A碰到黑色隔板后,会立刻消失;
3. 当A碰到红色隔板后,会进入环境。 如果我们想知道当大量粒子A从上图中P位置向右水平射出,会有多少个粒子通过红色隔板进入环境,就可以利用蒙特卡洛程序进行大量模拟。 对单个事例,当粒子A从P点出发前进1米后,抽取伪随机数N为[0,1]的均匀分布,根据抽取的数字决定其下一步的运动轨迹:当0
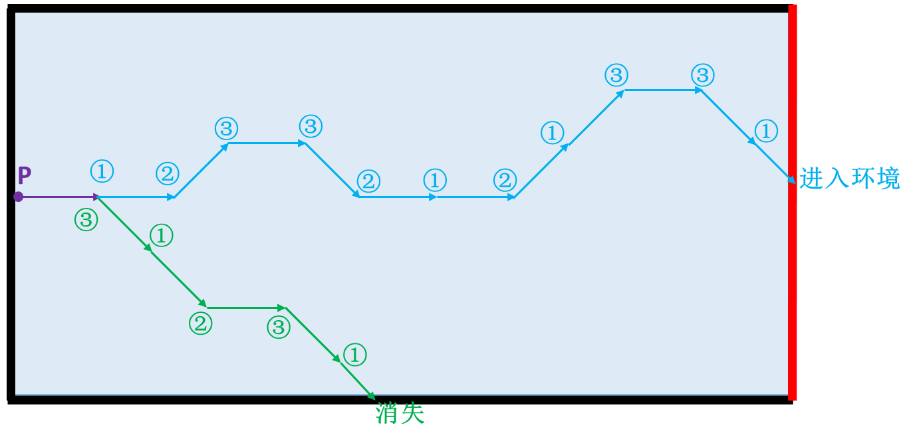
下图给出了粒子A可能的两种运行轨迹,利用计算机程序可以高效地完成大量的粒子模拟,得到计算结果。根据统计学特性,计算的事例越多,结果也就越接近期望值。
图 粒子A可能的两种运行轨迹
在理解了上述示例的计算思路后,不难想象在辐射防护领域的研究中,只要我们知道了粒子在运行过程中每一步可能发生的反应类型及其概率等基本的核物理参数,就可以通过计算机程序实现各种不同情形的模拟计算。
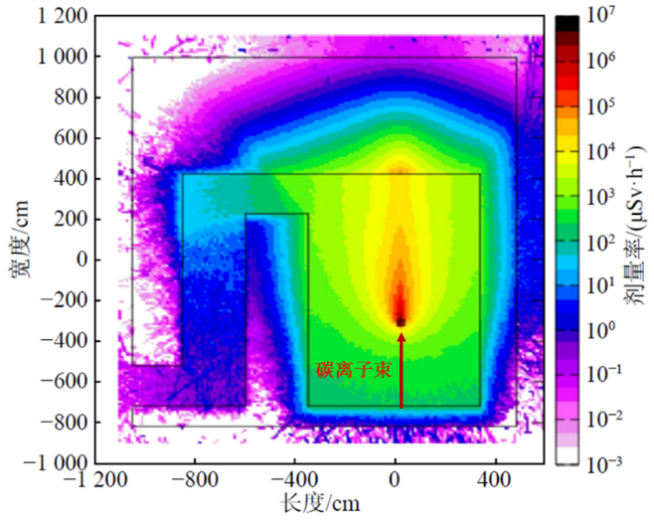
比如FLUKA程序可被用于计算国内医用重离子加速器HIMM治疗室的辐射剂量率分布。如下图所示,可以看出碳离子集中损失的位置辐射剂量率最高,约为106μSv/h;而经过混凝土屏蔽后,屏蔽外的辐射剂量率衰减到了2.5μSv/h以下。
图 HIMM治疗室剂量率分布图。HIMM装置每秒钟能够产生1亿个最高能量为400MeV/u的碳离子束用于治疗,束流照射人体时几乎全部损失,从而产生各种次级辐射。
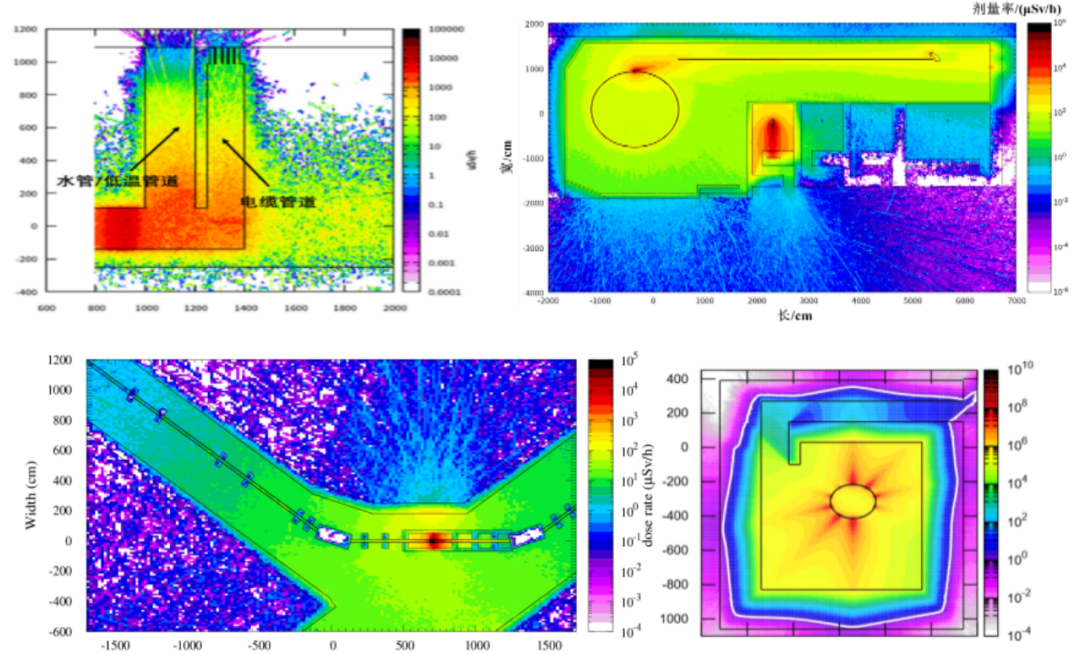
利用FLUKA程序,还可以开展更为复杂的辐射防护模拟研究,如更加多样的束流损失模式、更多的粒子种类与能量、更加复杂的建筑结构等。
图 各类加速器辐射剂量分布图示例
读到这里,相信大家对蒙特卡洛方法已经有了一个基本的了解。
审核编辑 :李倩
-
算法
+关注
关注
23文章
4601浏览量
92671 -
蒙特卡洛
+关注
关注
0文章
13浏览量
8154
原文标题:有趣的“赌博算法”——蒙特卡洛方法
文章出处:【微信号:bdtdsj,微信公众号:中科院半导体所】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
波特率的定义和计算方法 波特率与数据传输速度的关系
电流计算方法与配线法的区别
电荷放大电路的带宽 和IV转换电路带宽计算方法不一样吗?
机器学习中的交叉验证方法
储能容量的计算方法
电压探头延迟计算方法及应用

电线安全载流量的计算方法
耐压测试中漏电流的计算方法
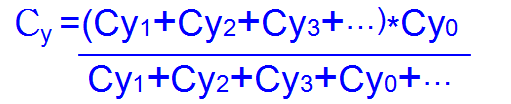
IGBT工作时序及门极驱动计算方法





 非常重要和有趣的计算方法——蒙特卡洛方法
非常重要和有趣的计算方法——蒙特卡洛方法












评论