在1930年代,Hendrik Wade Bode创造了一种直观的增益/相位方法,以电路的稳定性为唯一目标。这变成了现在所谓的波特图,一种直观地图形显示电路或放大器的增益、相位和反馈系统随频率的变化。
鉴于其有用性和重要性,让我们花一些时间应用波特稳定性分析技术来研究开环放大器和电路反馈因子大小,单位为分贝(dB)和相位响应(以度为单位)。本博客将探讨这些概念,并建议当您的主要目标是频率稳定性时如何避免设计“莺莺”电路。
要练习此技术,您可以从在线Digi-Key 创新手册中的资源下载波特图的可打印版本。
单极波特图
单极电路的配置允许直流V在直接转到 V 的信号 外 ,而在较高的输入频率下,V外等于零分贝 (dB)。波特图的构造很简单。y 轴单位是对数频率,线性 x 轴是以分贝为单位的增益或以度为单位的相位。在设计波特图时,您可以应用大量公式,但让我们切入快速求解方法。
波特图的简单之处在于,绘制图形只需要一个直边工具和一些规则的知识(图 1)。
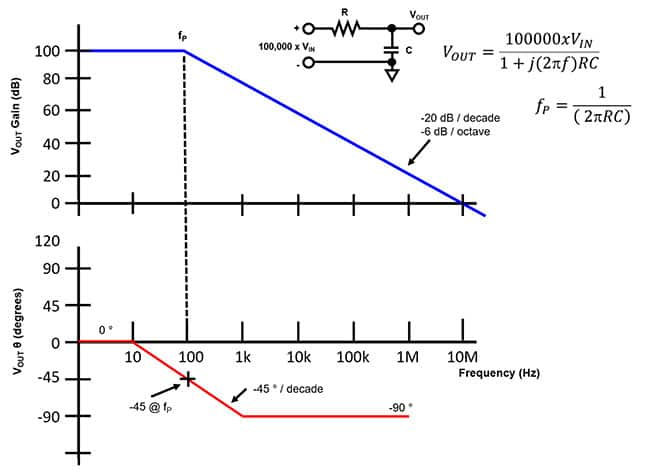 图 1:说明幅度和相移的单极点波特图使用直线来说明电路的频率和相位响应。(图片来源:邦妮·贝克)
图 1:说明幅度和相移的单极点波特图使用直线来说明电路的频率和相位响应。(图片来源:邦妮·贝克)
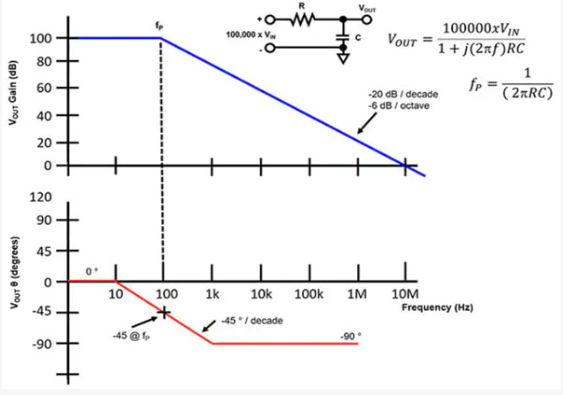
图1中的两个曲线表示单极点电阻/电容对的频率与增益和相位的关系。顶部和底部图的 x 轴频率范围为 1 赫兹 (Hz) 到 10 兆赫兹 (MHz)。顶部图 y 轴范围为 0 分贝 (dB) 到 100 dB,1 Hz 信号值等于 100 dB。该值与 100,000 x V 的增益因数一致 在 .蓝色曲线是单极点在f处的增益响应P或 100 Hz,其中 R 等于 159 千欧姆 (kΩ),C 等于 10 纳法拉 (nF)。
当频率超过极点频率(f P ),蓝色曲线以 -20 dB/十倍频程或 -6 dB/倍频程速率下降。该衰减率是要记住的第一个波特图经验法则:电路中的每个极点都以-20 dB/十倍频程的速率下降,从极点频率开始。因此,如果两个极点衰减 V外在相同的频率范围内,衰减率为-40 dB/十倍频程。
图1底部图表示该单极点电路的相位。在 1 Hz 时,R/C 网络的相位为 0 度 (°)。在十年前 f P ,或在本例中为 10 Hz,单极相位开始以 -45°/十倍频程下降,朝其 -90° 目标方向下降。
有几条规则适用于极点的相位响应。极点电路的第二个波特图经验法则是相位在f处等于-45° P .第三和第四个波特图规则描述了衰减和完成的相位点。单极相位在极点频率前十年开始下降(f P ),最终在十年后安定下来。P在-90°。
单零波特图
单零波特图反映了单极波特图的相反规则。R和C的位置以相同的值切换,以防止DC V在电压,同时允许更高的频率通过电容器(图 2)。
 图 2:说明幅度和相移的单零波特图。(图片来源:邦妮·贝克)
图 2:说明幅度和相移的单零波特图。(图片来源:邦妮·贝克)
当频率增加超过 f 时 Z ,蓝色曲线以 +20 dB/十倍频程上升。图2底部图表示该单零电路的相位。在十年前 f Z ,单零相位开始以+45°/十倍频程的速度上升,达到其+90°目标。零回路相位在 f 时等于 +45° Z .
为了总结图1中的值,极点位置为f P ,以及f之后的增益幅度P具有 -20 dB/十倍频程斜率。该相位的斜率为-45°/十倍频程,通过f P ,相位在 0.1x f 处开始衰减P并在 10 x f 时稳定至 -90° P .为了总结图 2 中的值,零位置为 f Z ,以及f之后的增益幅度Z具有 +20 dB/十倍频程斜率。该相位具有 +45°/十倍频程斜率,通过 f Z ,相位在 0.1 x f 处开始衰减Z并在 10 x f 时稳定至 +90° Z .
放大器开环波特图
标准运算放大器(op-amp)产品的频率操作可以在从亚赫兹到零dB截止频率的传递函数中具有多个极点和零点。放大器博德图没有魔力;只需遵循规则(图3)。

图3:运算放大器的可能波德图,显示了幅度和相移。(图片来源:Bonnie Baker)
图3所示为具有两个极点(f1和 f 2 ) 在传递函数中。使用两个极点时,增益每次下降-20 dB/十倍频程,相位总共下降到-180度。
在这一点上,我们在如何构建波特图方面有一个良好的开端,但让我们继续走向现实世界,其中有一个反馈系统。
闭环放大器系统稳定性
如果您花一些时间查看运算放大器电路,您总会发现反馈网络徘徊。经典运算放大器反馈网络具有增益正激元件(A 老 (jω))和反馈元件(β(JΩ))。
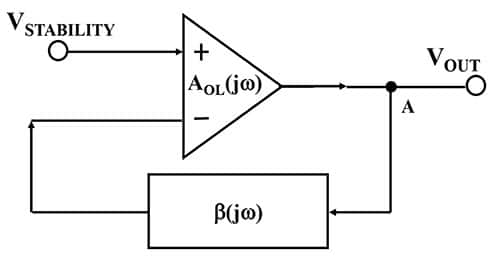 图 4:具有前馈元件 (AOL(jω)) 和反馈元件 (β(jω)) 的经典运算放大器反馈网络。(图片来源:邦妮·贝克)
图 4:具有前馈元件 (AOL(jω)) 和反馈元件 (β(jω)) 的经典运算放大器反馈网络。(图片来源:邦妮·贝克)
在图4中,运算放大器的开环增益(A 老 )比较大,反馈因子比较小。此配置将输出发送回反相端子,从而产生负反馈条件,在该条件下,该反馈使输出处于控制之下。我们将使用β或1/β的倒数来确定运算放大器电路的稳定性。
计算 1/β 的最简单方法是放置一个源,称为 V 稳定性 ,在运算放大器的同相输入上。这种计算策略将为确定电路的稳定性提供极好的途径(图 5)。
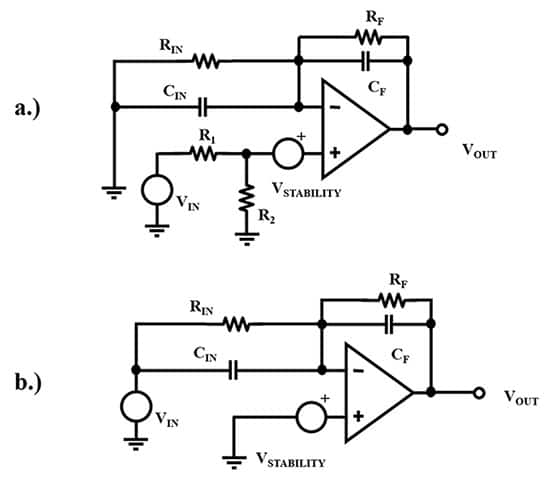 图 5:同相运算放大器电路 a.)和反相运算放大器电路 b.)两者都有一个虚构的 V稳定性同相输入端的电压源,可精确计算电路的1/β系数或噪声增益。(图片来源:邦妮·贝克)
图 5:同相运算放大器电路 a.)和反相运算放大器电路 b.)两者都有一个虚构的 V稳定性同相输入端的电压源,可精确计算电路的1/β系数或噪声增益。(图片来源:邦妮·贝克)
如果检查图5中的电路,会注意到从同相端子到输出的反馈电路是相同的。V的位置稳定性电压源可以精确计算电路的1/β系数或噪声增益。
1/β稳定性分析使用 V 稳定性 .如果假设运算放大器开环增益为无穷大,则两个电路的传递函数等于:
 等式 1
等式 1
 等式2
等式2
 等式3
等式3
当公式3的频率分量jω等于零时:
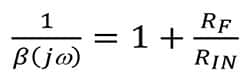 等式 4
等式 4
当jω在公式3中接近无穷大时:
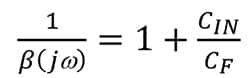 等式5
等式5
1/β 零 (f Z ) 和极点 (f P ) 是:
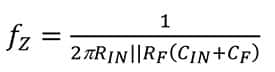 等式 6
等式 6
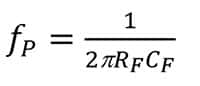 公式7
公式7
符合上述规则的1/β稳定性分析曲线的Bode图如图6所示。

图6:图5 a)和b)的1/β频率响应相同。零点出现在较低频率,极点出现在较高频率。(图片来源:Bonnie Baker)
图6描述了运算放大器电路的1/β或噪声增益的频率和相位响应。该图以图形形式总结了方程4至7。方程4和5定义了DC增益和¥增益,包括在内。等式6和7包括电路的零点和极点。图3和图6中的信息提供了通过定义系统的传递函数以及极点和零点的位置来建立运算放大器电路稳定性的第一步。最后一步是将图3和图6叠加到一个图中。
系统稳定性测定
开环和闭环增益的交集或闭合率定义了电路的相移。通常,闭合率小于或等于30dB表示电路稳定。大于30 dB的闭合率正在向不稳定电路状态移动(图7)。
 图 7:运算放大器的 AOL 增益和相位响应与 1/β 增益和相位响应叠加。(图片来源:邦妮·贝克)
图 7:运算放大器的 AOL 增益和相位响应与 1/β 增益和相位响应叠加。(图片来源:邦妮·贝克)
在图7中,AOL和1/β增益曲线之间的闭合速率等于40 dB。40 dB闭合速率表示相移大于135°,表示电路不稳定。在这种配置下,180°的闭合速率会产生一个振荡的电路。
上述问题有很多解决方案。电阻或电容值可以通过移动极点和零点频率来改变。另一种选择是选择不同的运算放大器(图 8)。

在不改变零点和极点频率的情况下,使用带宽高于图7运算放大器的运算放大器”)图 8:使用带宽高于图 7 中运算放大器的运算放大器,而不改变零点和极点频率。(图片来源:邦妮·贝克)
在图8中,运算放大器带宽高出约二十倍频程,而无需改变1/β网络。绿色虚线反映实际计算,并提供更真实的波特图。放大器带宽的增加将闭合速率从40 dB更改为20 dB。由此产生的相移现在为~105°,表明电路稳定。
图 8 中的绿色虚线超越了波特图的标尺和铅笔创建,包括了现实世界的响应。
测量电路增益和相位
测量放大器电路的增益和相位需要一个提供输入信号的函数发生器以及一个网络分析仪(图 9)。代表是泰博尔电子 LS3081B3 GHz RF模拟扫描函数发生器。
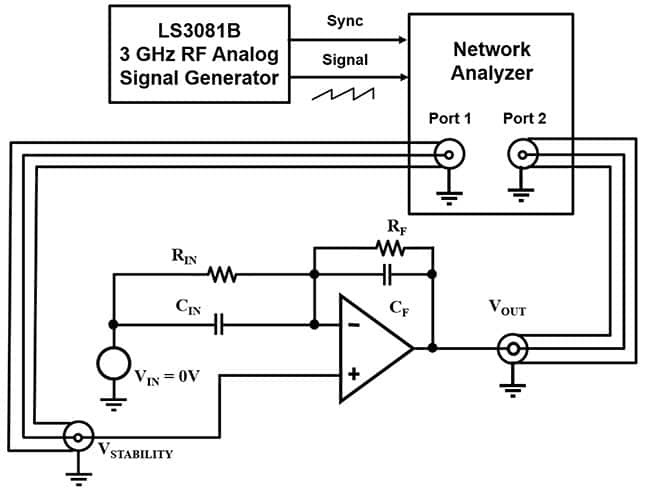
图5反相放大器电路的增益和相位测量配置”)图 9:图 5 b)的增益和相位测量配置s反相放大器电路。(图片来源:邦妮·贝克)
在图9中,函数发生器输入信号的应用发生在端口1至V处稳定性节点。信号通过放大电路传播到电路的输出(V 外 ),其中网络分析仪捕获端口 2 处的信号,并将其与函数发生器的端口 1 信号进行比较。
结论
在设计稳定的运算放大器电路时,波特图是添加到套件中的非常有用的工具。当您开始查看多极点和多零点电路时,波特图背后的功耗变得显而易见,其中放大器开环增益和反馈网络之间的闭合速率快速定义了电路的稳定性。
虽然本博客可以通过展示在方格纸上简单使用直边来估计一阶极点和零点电路的增益与相位来帮助掌握波特图的使用,但最好的学习方法是练习。同样,您可以从在线 Digi-Key 创新手册中的资源下载波特图的可打印版本。
审核编辑 黄昊宇
-
电路
+关注
关注
173文章
5979浏览量
173140 -
波特图
+关注
关注
1文章
29浏览量
11362
发布评论请先 登录
相关推荐
运放的稳定性仿真分析

如何测试电源设计的稳定性测量
使用SPICE工具检测电路稳定性的方法
运放电路稳定性,这篇给你讲全了!
判定系统稳定性的充分必要条件是什么?
如何运用波特图来确保电路的稳定性




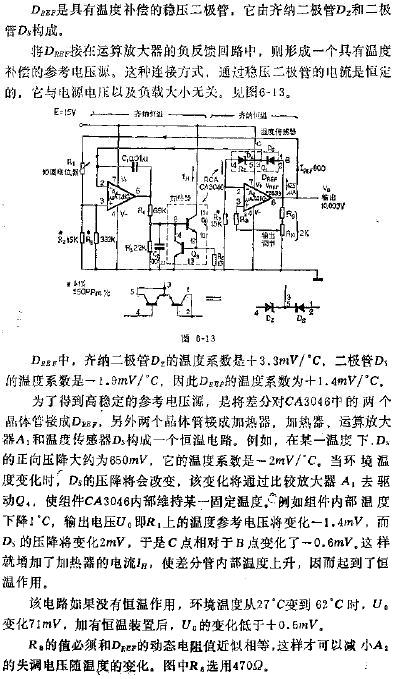
 如何运用波特图的力量来确保电路稳定性
如何运用波特图的力量来确保电路稳定性










评论