在本系列的第一篇文章中,检查了滤波器阶段与滤波器实现拓扑的关系。在第二篇文章中,检查了低通和高通响应的滤波器传递函数的相移。本文将重点介绍带通响应。虽然滤波器主要针对其幅度响应而设计,但相位响应在某些应用中可能很重要。
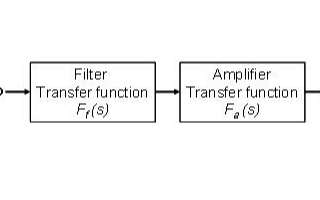
为了便于审查,有源滤波器的传递函数实际上是滤波器传递函数和放大器传递函数的级联(见图1)。

图1.滤波为两个传递函数的级联。
带通传递函数
将低通原型的分子更改为
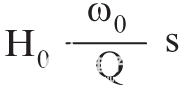
将滤波器转换为带通功能。这将在传递函数中放置一个零。分子中的 s 项给了我们一个零,分子中的 s 项给了我们一个极点。零将给出频率上升响应,而极点将给出频率下降响应。
二阶带通滤波器的传递函数为:
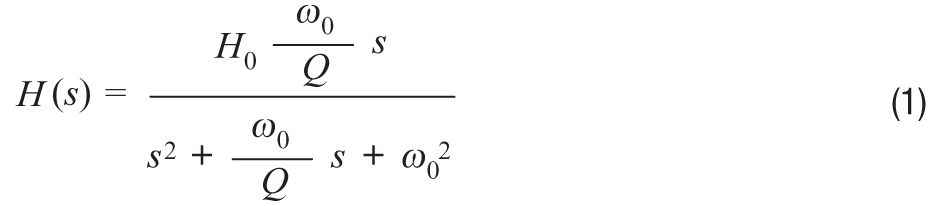
ω0 这里是频率 (F0= 2 π ω0),此时滤波器的增益达到峰值。
H0是电路增益(Q峰值),定义为:

其中 H 是滤波器实现的增益。
Q对于带通响应具有特殊含义。它是过滤器的选择性。它被定义为:

其中 FL 和 FH 是响应从最大值开始 –3 dB 的频率。
滤波器的带宽 (BW) 描述为:

可以证明谐振频率(F0) 是 F 的几何平均值L和 FH,这意味着 F0将出现在 F 之间的中间L和 FH在对数刻度上。

另外,请注意,带通响应的裙边将始终围绕F对称0在对数刻度上。
带通滤波器对各种Q值的幅度响应如图2所示。在此图中,中心频率处的增益归一化为1 (0 dB)。
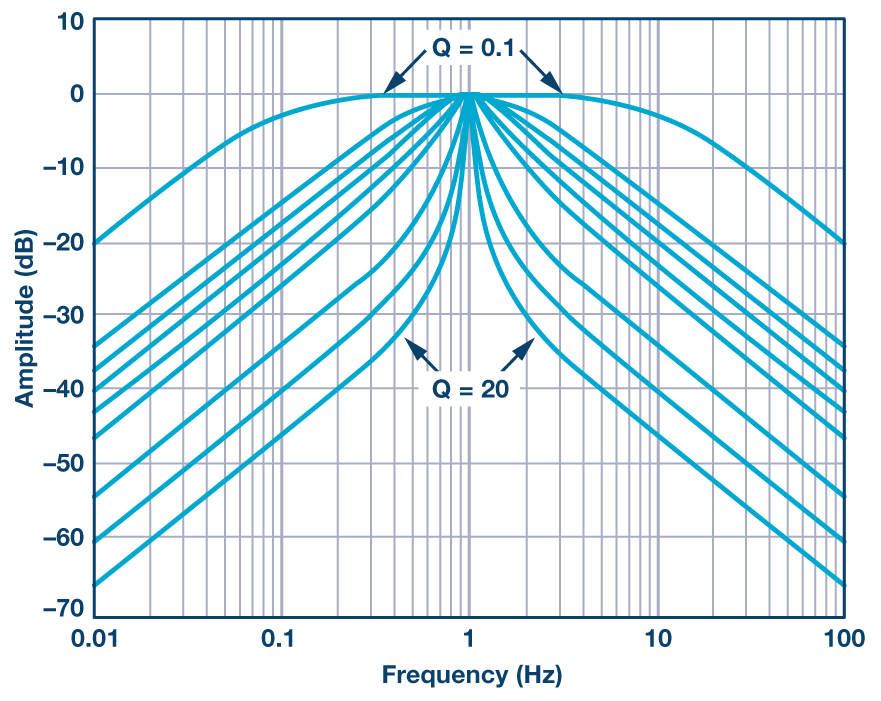
图2.归一化带通滤波器幅度响应。
同样,本文主要关注相位响应,但了解滤波器的幅度响应很有用。
在这里要注意一句话是恰当的。带通滤波器可以通过两种不同的方式定义。窄带情况是我们上面显示的经典定义。然而,在某些情况下,如果高截止频率和低截止频率相距甚远,则带通滤波器由单独的高通和低通部分构成。在这种情况下,广泛相距意味着至少相隔两个八度(频率为×4)。这是宽带情况。我们主要关注本文的窄带情况。对于宽带情况,将滤波器评估为单独的高通和低通部分。
虽然带通滤波器可以根据标准响应来定义,例如巴特沃斯、贝塞尔或切比雪夫,但它们通常也由其Q和F定义0.
带通滤波器的相位响应为:
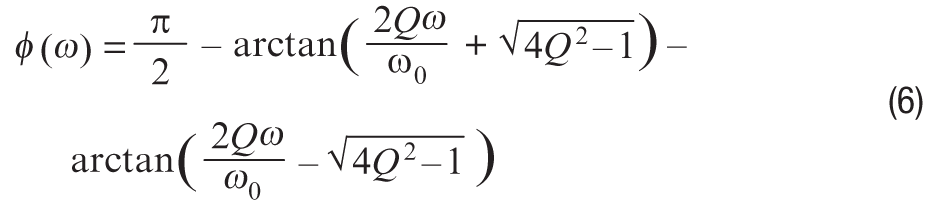
请注意,没有单极点带通滤波器这样的东西。
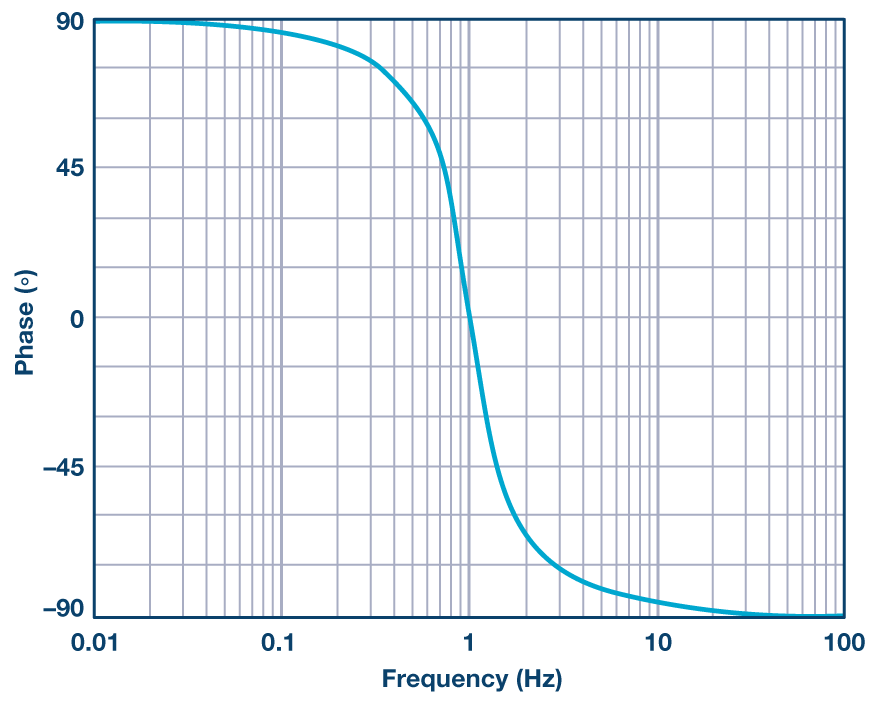
图3.归一化带通滤波器相位响应。
图3评估了公式6从低于中心频率二十倍频到高于中心频率二十倍频的曲线。中心频率的相移为0°。中心频率为1,Q为0.707。这与上一篇文章中使用的 Q 相同,尽管在那篇文章中我们使用了α。请记住α = 1/Q。
检查显示,该曲线的形状与低通曲线(以及高通曲线)的形状基本相同。然而,在这种情况下,相移从低于中心频率的90°到中心频率的0°到高于中心频率的–90°。
在图4中,我们研究了带通滤波器在Q值变化时的相位响应。如果我们看一下传递函数,我们可以看到相位变化可以在相对较大的频率范围内发生,并且变化的范围与电路的Q成反比。同样,检查表明曲线与低通(和高通)响应的曲线具有相同的形状,只是范围不同。
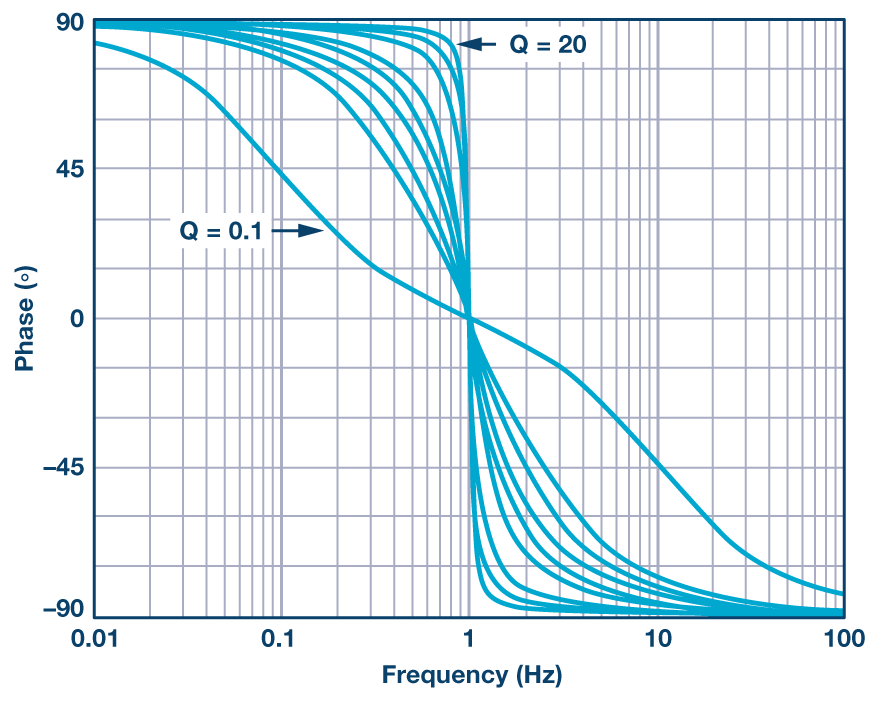
图4.具有不同Q值的归一化带通滤波器相位响应。
放大器传递函数
在前几期中已经表明,传递函数基本上是单极点滤波器的传递函数。虽然放大器的相移通常被忽略,但它会影响复合滤波器的整体传输。本文任意选择AD822用于滤波器仿真。选择它部分是为了尽量减少对滤波器传递函数的影响。这是因为放大器的相移频率远高于滤波器本身的转折频率。AD822的传递函数如图5所示,该信息直接取自数据手册。
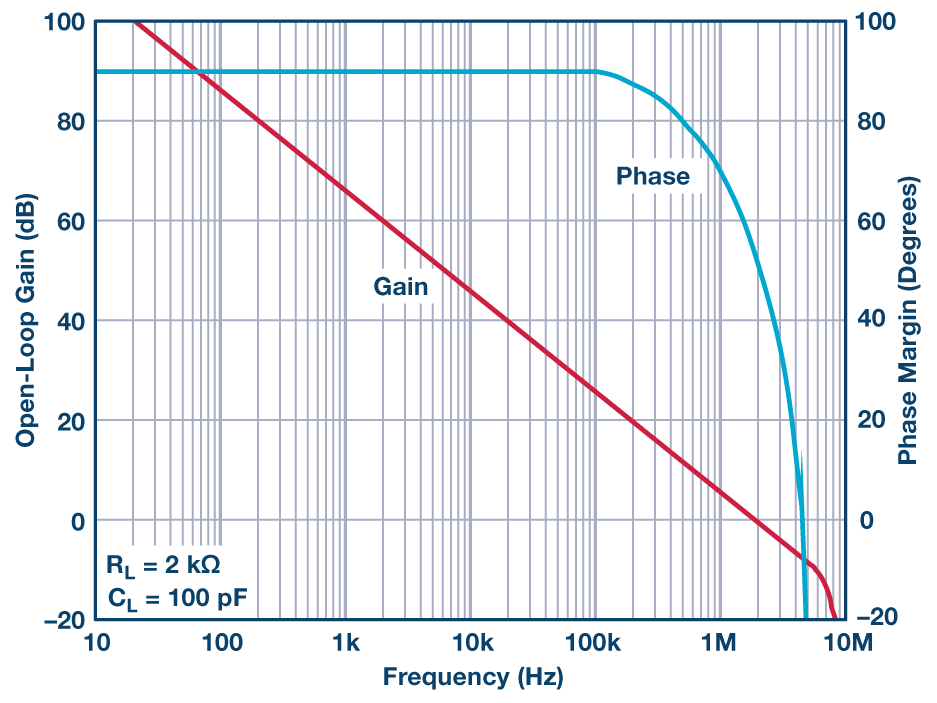
图5.AD822波特图增益和相位。
示例1:Q = 20的1 kHz、2极点带通滤波器
第一个例子是从一开始就设计为带通的滤波器。我们任意选择1 kHz的中心频率和20的Q。由于Q值偏高,我们将使用双放大器带通(DABP)配置。同样,这是一个任意的选择。
我们使用参考文献 1 中的设计公式。合成电路如图6所示:
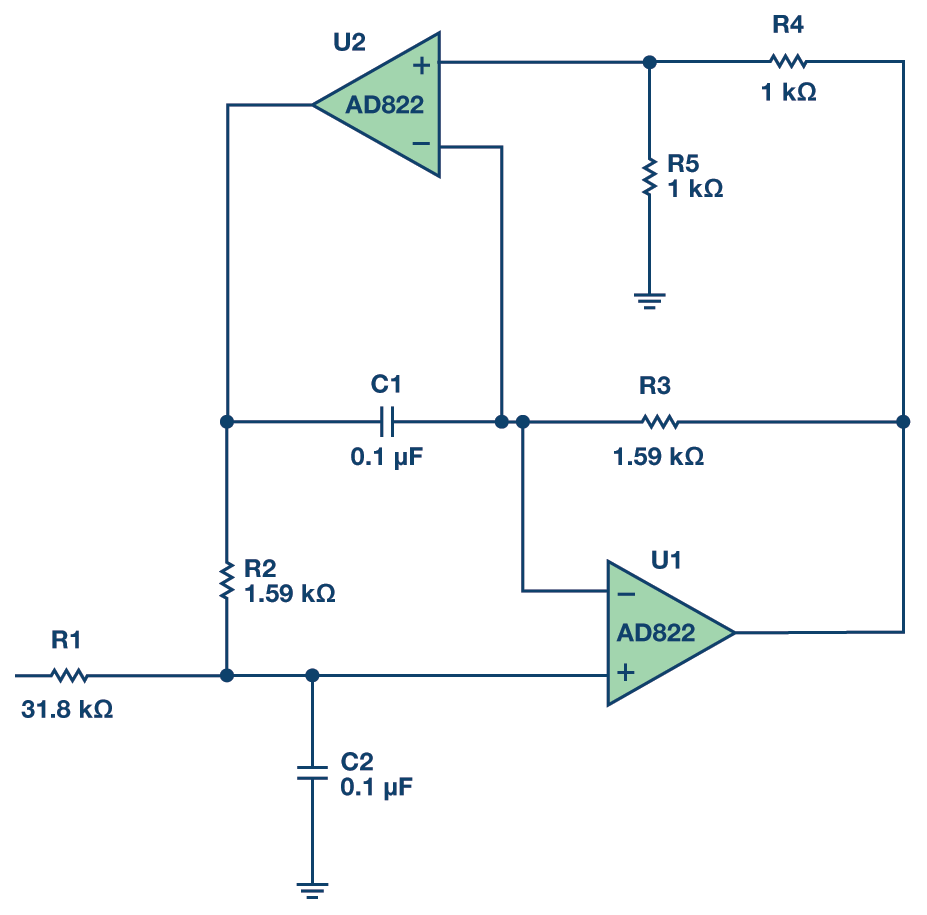
图6.1 kHz,Q = 20 DABP带通滤波器。
在本文中,我们主要关注相位,但我认为检查幅度响应很有用。
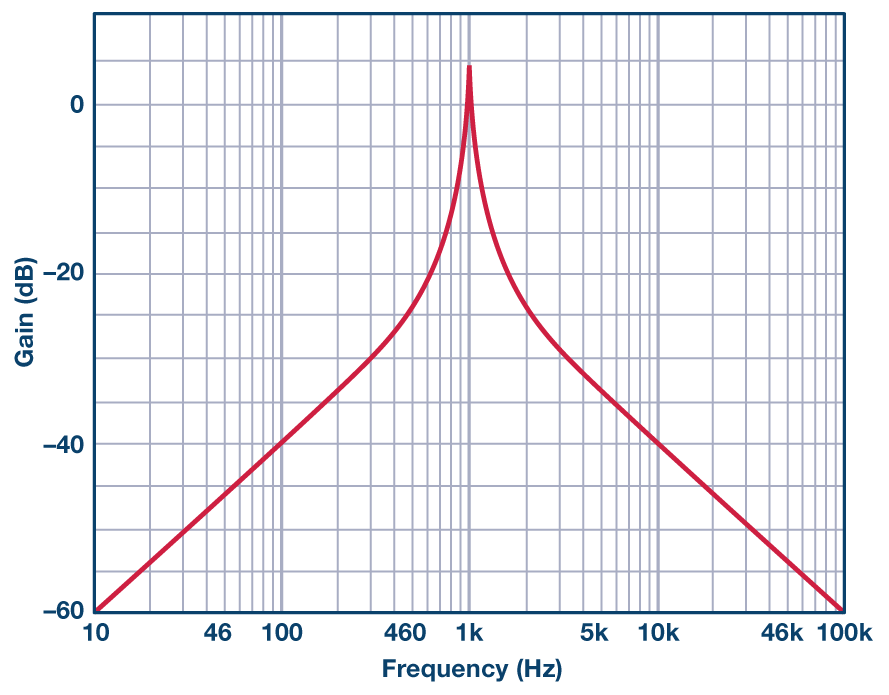
图7.1 kHz,Q = 20 DABP带通滤波器幅度响应。
我们在图8中看到相位响应:
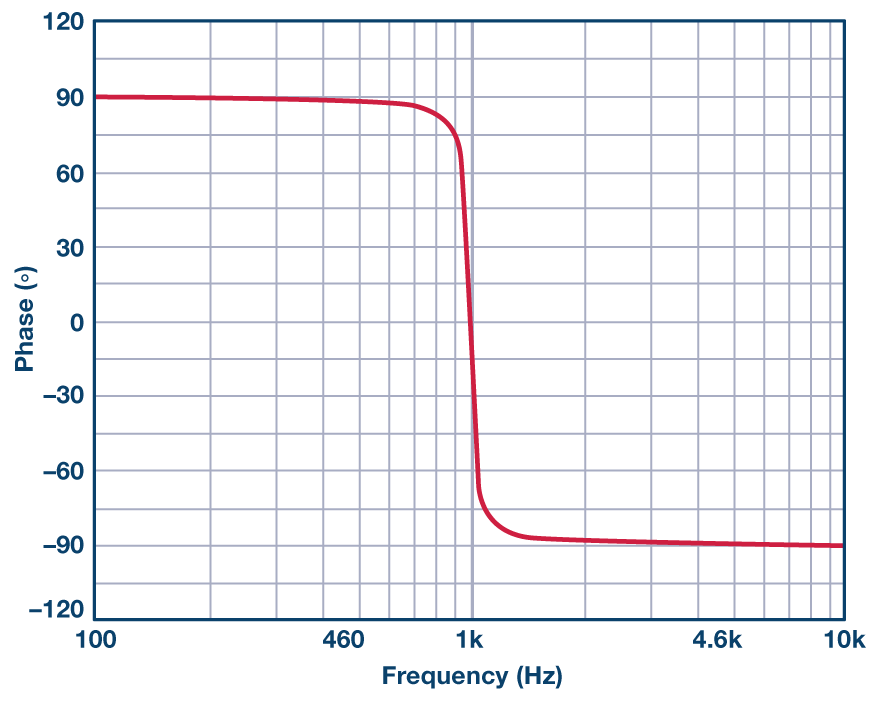
图8.1 kHz,Q = 20 DABP带通滤波器相位响应。
请注意,DABP 配置是同相的。图 8 与图 3 匹配。
示例2:1 kHz、3极点0.5 dB切比雪夫低通至带通滤波器变换
滤波器理论基于低通原型,然后可以将其操纵成其他形式。在本例中,将使用的原型是1 kHz、3极点、0.5 dB切比雪夫滤波器。选择切比雪夫滤波器是因为如果响应不正确,它会更清楚地显示。例如,通带中的波纹不会对齐。在这种情况下,巴特沃斯过滤器可能太宽容了。选择3极点滤波器,以便变换极点对和单极点。
LP原型的极点位置(来自参考文献1)为:
| 阶段 | α | β | F0 | α |
| 1 | 0.2683 | 0.8753 | 1.0688 | 0.5861 |
| 2 | 0.5366 | 0.6265 |
第一阶段是极对,第二阶段是单极。请注意对两个完全独立的参数使用 α 的不幸约定。左侧的α和β是 s 平面中的极点位置。这些是转换算法中使用的值。右边的α是1/Q,这是物理滤波器的设计公式想要看到的。
低通原型现在转换为带通滤波器。参考文献 1 中概述的公式字符串用于转换。原型滤波器的每个极点将转换为一极对。因此,3极原型在转换时将具有六个极(3极对)。此外,原点将有六个零。没有单极带通这样的东西。
转换过程的一部分是指定所得滤波器的3 dB带宽。在这种情况下,此带宽将设置为 500 Hz。转换结果:
| 阶段 | F0 | Q | 答0 |
| 1 | 804.5 | 7.63 | 3.49 |
| 2 | 1243 | 7.63 | 3.49 |
| 3 | 1000 | 3.73 | 1 |
实际上,将较低增益、较低Q值的部分放在串中的第一个位置可能会很有用,以最大限度地提高信号电平处理能力。前两级增益要求的原因是它们的中心频率将相对于总滤波器的中心频率衰减(即,它们将位于其他部分的裙边)。
由于得到的Q是中等的(小于20),因此将选择多重反馈拓扑。参考文献1中多反馈带通滤波器的设计公式用于设计滤波器。图9显示了滤波器本身的原理图。
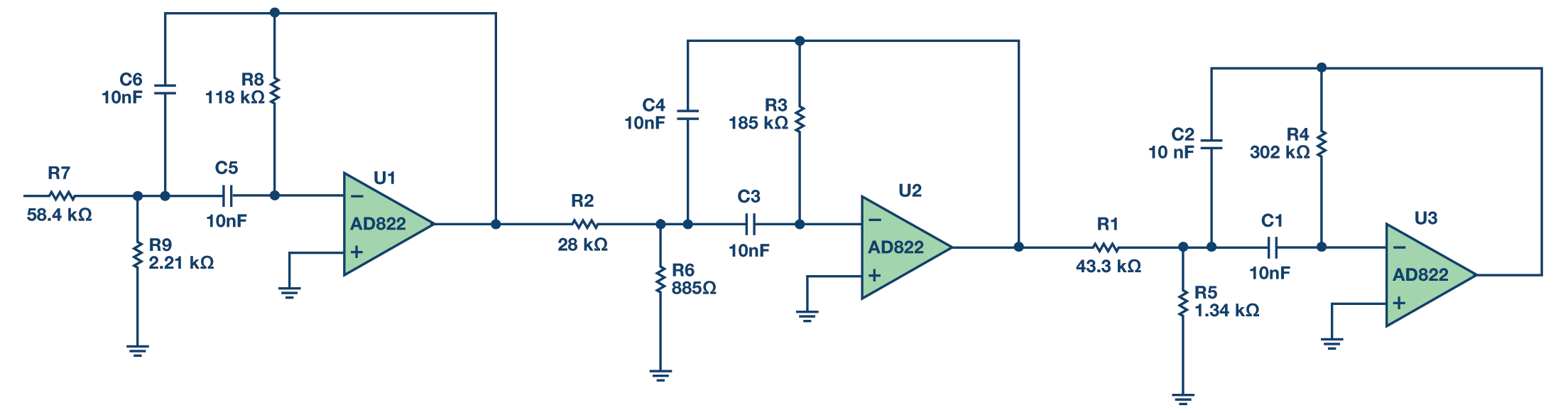
图9.1 kHz、6 极点、0.5 dB 切比雪夫带通滤波器。
在图10中,我们查看了整个滤波器的相移。该图显示了单独第一部分(第1部分)、前两部分一起(第2部分)和整个滤波器(第3部分)的相移。这些显示了“实际”滤波器部分的相移,包括放大器的相移和滤波器拓扑的反转。
图 10 中有几个细节需要注意。首先,相位响应是累积的。第一部分显示了180°的相位变化(滤波器函数的相移,不考虑滤波器拓扑的相移)。第二部分显示了360°的相变,这是由于有两个部分,两个部分各180°。请记住,360° = 0°。第三部分显示了540°的相移,每个部分为180°。另请注意,在高于10 kHz的频率下,由于放大器响应,我们开始看到相位略有滚降。我们可以看到,滚降再次是累积的,每个部分都在增加。
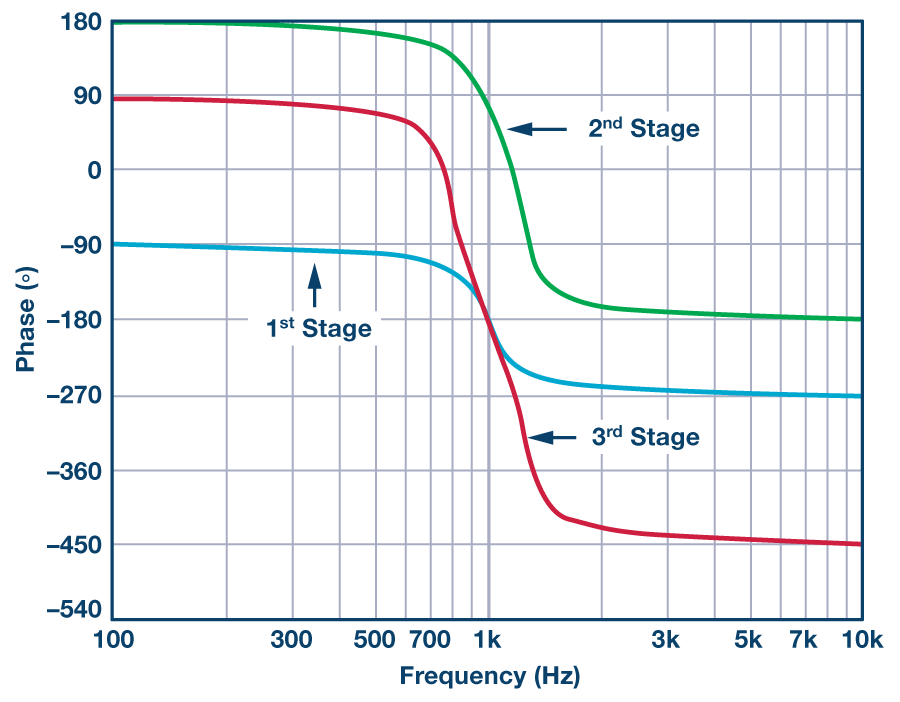
图 10.1 kHz、6极点、0.5 dB切比雪夫带通滤波器的相位响应。
在图11中,我们可以看到整个滤波器的幅度响应。
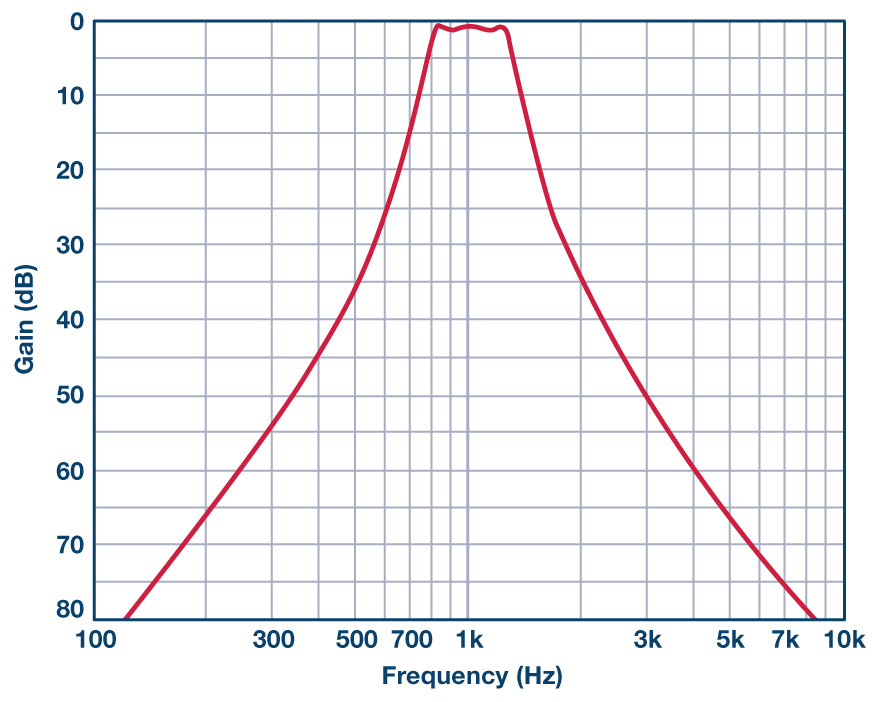
图 11.1 kHz、6 极点、0.5 dB切比雪夫带通滤波器的幅度响应。
结论
本文考虑带通滤波器的相移。在本系列的前几篇文章中,我们研究了与滤波器拓扑以及高通和低通拓扑相关的相移。在以后的文章中,我们将介绍陷波和全通滤波器。在最后一部分中,我们将将它们联系在一起,并研究相移如何影响滤波器的瞬态响应,研究群延迟、脉冲响应和阶跃响应,以及这对信号意味着什么。
审核编辑:郭婷
-
放大器
+关注
关注
143文章
13586浏览量
213380 -
滤波器
+关注
关注
161文章
7799浏览量
178012
发布评论请先 登录
相关推荐
有源滤波器
有源滤波器相位响应
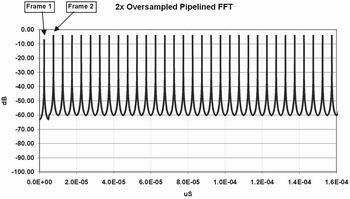
FFT、PFT和多相位DFT滤波器组瞬态响应的比较
有源电力滤波器分类
有源滤波器中的低通和高通响应的计算和相移分析




 有源滤波器中的相位响应
有源滤波器中的相位响应













评论