作者:Vicky Wong and Yoshinori Kusuda
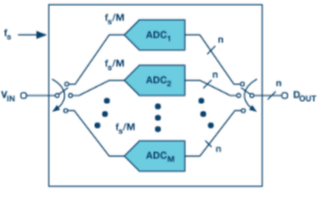
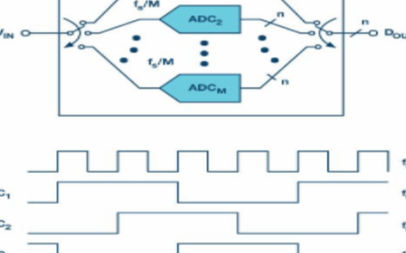
时间交错是一种允许使用多个相同的模数转换器的技术[1](ADC)以比每个单独数据转换器的工作采样速率更快的速率处理常规采样数据系列。简单来说,时间交错(IL)包括对M个相同ADC的并行阵列进行时间多路复用,如图1所示,以实现更高的净采样速率。fs(带采样周期Ts = 1/fs),即使阵列中的每个 ADC 实际上都以较低的速率采样(和转换)fs/米.因此,例如,通过交错四个10位/100 MSPS ADC,原则上可以实现一个10位/400 MSPS ADC。
为了更好地理解IL的原理,图1中模拟输入V。在(t) 由 M ADC 采样,并得出组合的数字输出数据序列D外.模数转换器1将采样 VIN(t0) 首先开始将其转换为 n 位数字表示。Ts几秒钟后,ADC2将样本五在(t0+ Ts) 并开始将其转换为 n 位数字表示形式。然后Ts几秒钟后,ADC3将样本五在(t0+ 2吨s)等等。在 ADCM 对 V 进行采样后在(t0 + (M – 1) × Ts),下一个采样周期从ADC1采样V开始在(t0+ 米 × Ts),这个旋转木马继续。
当ADC的n位输出按与采样操作相同的顺序提供时,这些数字n位字由同一图右侧所示的解复用器收集。这里重新组合的数据输出序列D外(t0+ 升),D外(t0+ 升 + 吨s),D外(t0+ L + 2Ts), ...获得。L代表每个ADC的固定转换时间,此重新组合的数据序列是具有采样速率的n位数据系列fs.因此,虽然单个ADC(通常称为“通道”)是n位ADC,采样速率为:fs/米,盒子中包含的融合相当于单个n位ADC采样fs,我们将其称为时间交错ADC(将其与通道区分开来)。基本上,输入由阵列中的ADC进行切片和单独处理,然后在输出端一致地重新组装以形成高数据速率表示D外的输入V在.
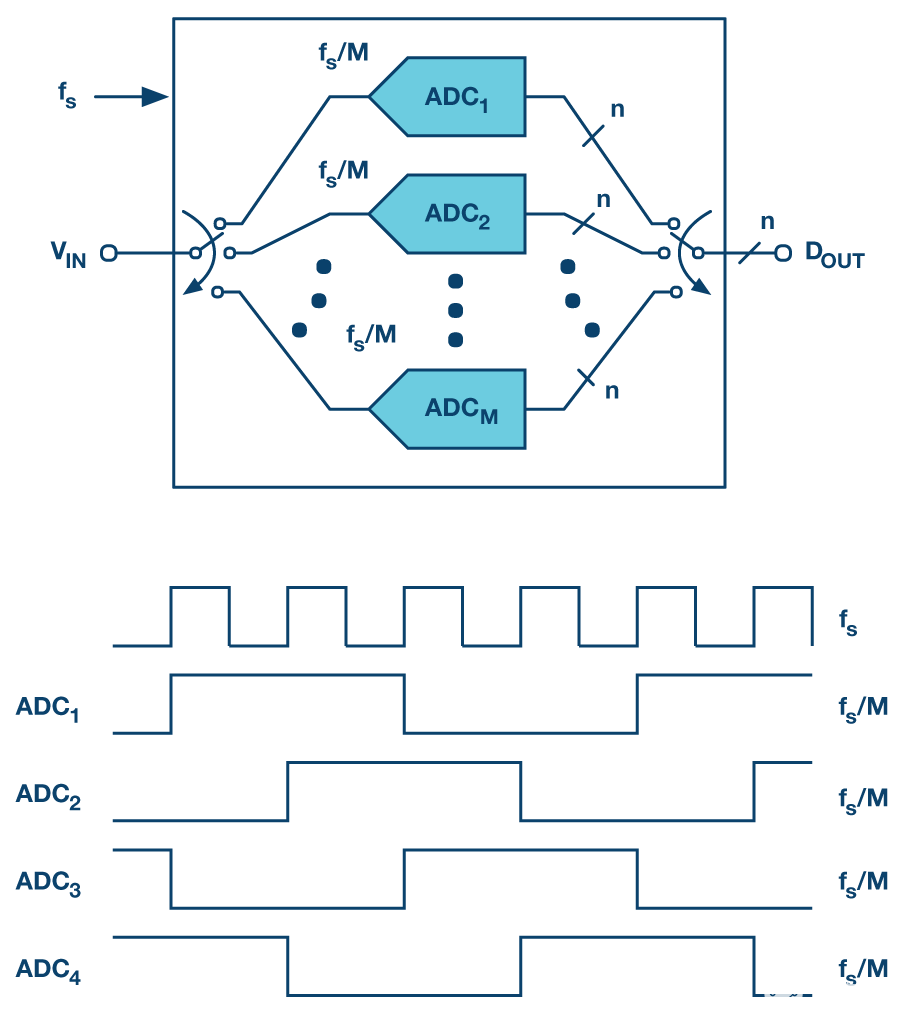
图1.M时间交错n位ADC阵列。每个的采样率为fs/米,得到的时间交错型ADC的采样速率为fs.该图的下半部分描述了M = 4情况下的时钟方案示例。
这种强大的技术并非没有实际挑战。当来自通道的M数据流以数字方式组合在一起以重建原始输入信号时,关键问题就显现出来了V在.如果我们看一下光谱D外,除了看到数字表示V在 以及模数转换引入的失真,我们还将看到额外的大量杂散内容,称为“交错杂散”(或简称IL杂散),IL杂散既不像高阶信号谐波那样具有多项式型失真的特征(2德·, 3RD等),也不是量化或 DNL 错误的签名。IL伪像可以看作是时域固定码型噪声的一种形式,是由通道中的模拟损伤引入的,由于交错过程,这些损伤与切片转换信号调制,最终出现在最终的数字化输出中D外.
让我们通过分析一个简单的例子来了解可能发生的事情。考虑具有正弦输入的双向交错ADC的情况V在 在频率f在.假设 ADC1有增益,G1和那个 ADC2有一个不同的增益,G2。在这种双向IL ADC中,ADC1和 ADC2将在采样中交替V在.所以如果 ADC1转换偶数样本和ADC2转换奇数样本,然后转换所有偶数数据D外振幅由 G 设定1,而所有奇数数据D外 振幅由 G 设定2.然后D外不仅包含V在 以及一些多项式失真,但它一直受到G的交替放大倍率的影响1和 G2就像我们在调幅一样V在 频率为方波fs/2.这将引入额外的虚假内容。具体说来D外将包括频率的“增益杂散”fs/2 –f在不幸的是,该杂散的频率跟踪输入f在 并且它位于交错 ADC 的第一奈奎斯特带内(即在fs/2)并且在所有其他奈奎斯特带上也有它的别名。这种交错杂散的功率/幅度取决于两个增益G之间的净差 1和 G2.换句话说,这取决于增益误差失配。[2]最后,这取决于输入的大小V在 本身。
如果输入不是简单的正弦波,而是像在实际应用案例中一样,它是一个全频段限制信号,那么“增益杂散”不仅仅是一个不需要的音调,而是出现在奈奎斯特频段内的带限制输入信号本身的完整缩放图像。这在某种程度上抵消了交错提供的带宽增加的好处。
虽然在上面的例子中,我们只考虑了通道之间的增益误差失配,但其他损伤也会引入交错杂散。失调失配(通道失调之间的差异)在固定频率下引入音调(“失调杂散”),功率与失调失配成正比。[3]当某些通道的采样时间比预期顺序早于或晚一点时,就会发生采样时间偏差。这引入了与增益杂散位于相同频率(并且加起来具有相同幅度)的“定时杂散”。[4]但随着权力越来越强大f在 随着输入幅度的增长而增长。各个通道之间的带宽不匹配会在频率上引入更多的杂散内容,具体取决于f在而且,就像时序杂散一样,杂散功率会随着f在本身,而不仅仅是输入幅度。同样,在所有情况下,输出频谱退化的严重程度不取决于通道损伤的绝对值(偏移、增益、时序、频段),而是取决于它们之间的相对不匹配/差异。
虽然时间交错的一般技术已经存在了几十年,但IL杂散可以保持在最低限度的程度限制了其过去对低分辨率转换器的适用性。然而,在通道失配校准和抑制残余IL杂散成分方面的最新进展,如今可以实现完全集成的超高速12位、14位和16位IL ADC。
此时,我们需要区分某些交错类。我们一般在两个交错通道的情况下称为“乒乓”操作。然后,我们可以区分“轻度交错”和“高度交错”,因为我们指的是通道数量减少的情况(例如,三个通道到四个通道)或大量通道的情况,例如分别说四个以上,通常为八个以上。
乒乓球(双向)交错
如图2(a)框图所示,当我们只交错两个通道以使净采样率加倍时,我们称之为“乒乓球”。这是一个特别简单的案例,具有一些有趣且有用的功能。在这种情况下,在 1圣交错ADC的奈奎斯特带,交错杂散位于直流,在fs/2和在fs/2 –f在.所以,如果输入信号V在 是窄带信号,中心在f在,如图2(b)的第一个奈奎斯特输出频谱所示,交错杂散将包括直流处的偏移杂散,另一个偏移失配杂散位于直流处fs/2,增益和时序杂散镜像居中fs/2 –f在 这看起来像输入本身的缩放副本。
如果输入信号V在(f) 完全绑定在 0 和fs/4,如图2(b)所示,交错杂散与数字化输入的频率不重叠。在这种情况下,坏消息是我们只能在奈奎斯特波段的一半进行数字化,即就像我们有一个单通道时钟一样fs/2,尽管我们仍然消耗至少两倍于这种单个通道的功率。奈奎斯特波段上端的交错杂散镜像可以在数字化后通过数字滤波抑制,并且不需要校正模拟损伤。
然而,好消息是,由于乒乓球ADC的时钟频率为:fs,数字化输出受益于动态范围内3 dB的处理增益。此外,与使用时钟频率为fs/2,乒乓球ADC的抗混叠滤波器设计有所放松。
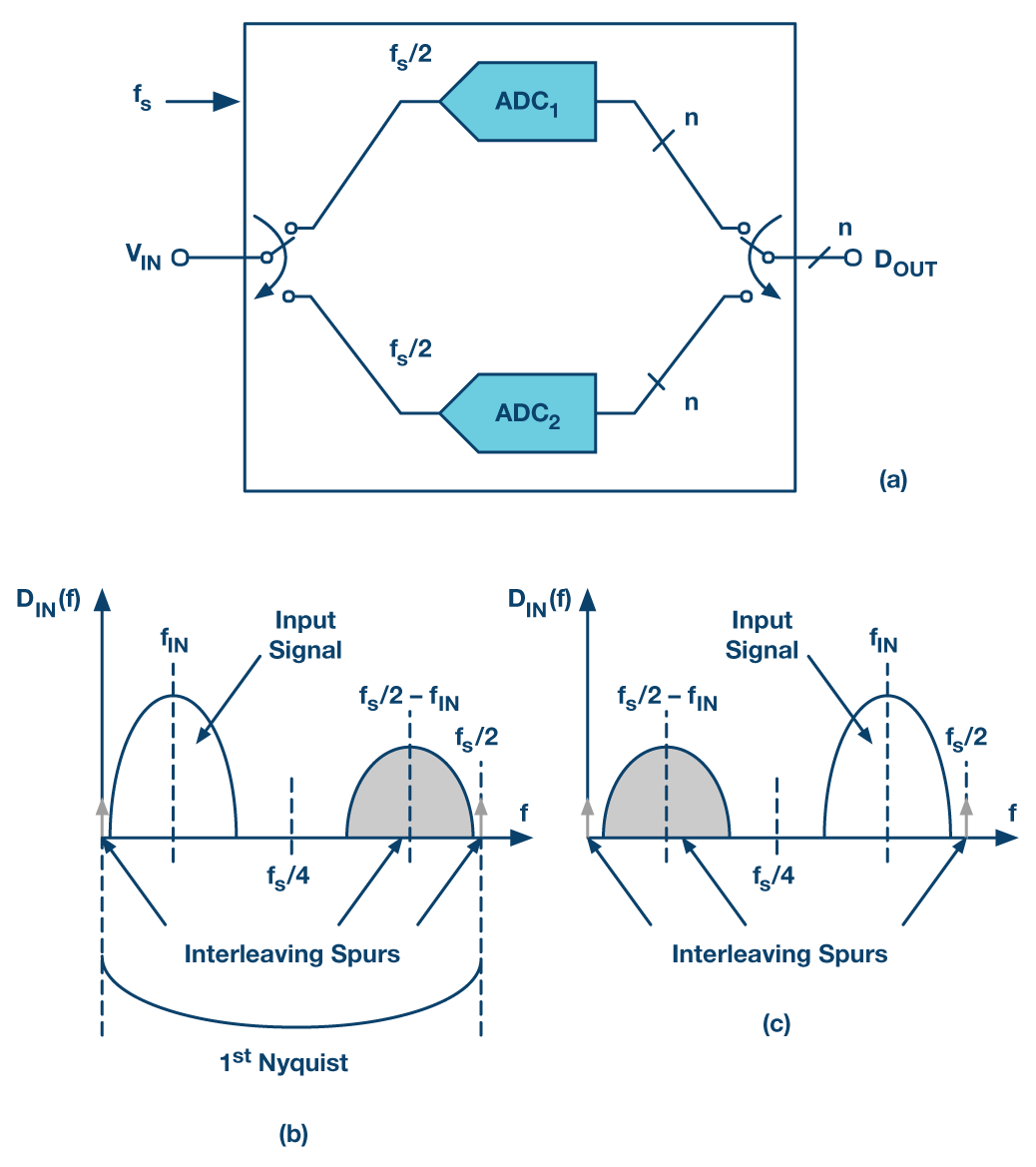
图2.(a) 乒乓球方案,(b) 窄带输入信号低于时的输出频谱fs/4 和 (c) 当输入信号位于fs/4和奈奎斯特频率fs/2.
如果窄带信号位于第一奈奎斯特频段的上半部分,则可以重复所有相同的考虑因素,如图2(c)所示,因为交错图像杂散移动到奈奎斯特频段的下半部分。同样,增益和时序杂散可以在数字化后通过滤波进行数字抑制。
最后,一旦输入信号频率位置越过fs/4行。在这种情况下,无法恢复所需的输入信号,并且乒乓球方案不可用。当然,除非通道间匹配足够接近,使交错杂散成分对于应用来说是可接受的低水平,或者采用校准来减少导致IL图像的原因。
总之,频率规划和一些数字滤波允许在乒乓方案中恢复窄带数字化输入,即使在存在信道不匹配的情况下也是如此。而与使用时钟频率为fs/2,乒乓方案提供3 dB处理增益,放宽抗混叠要求。
图3显示了未对通道失配及其产生的交错杂散进行任何校正的乒乓球示例。在这种情况下,双通道14位/1 GSPS ADC AD9680的两个ADC交替采样单个正弦波,因此以2 GSPS返回单个组合输出数据流。当我们看 1圣此乒乓方案输出频谱的奈奎斯特频段(介于直流和 1 GHz 之间)我们可以看到输入音调,这是左侧的强音调f在= 400 MHz,我们还可以看到强烈的增益/时序失配杂散fs/2 –f在= 2G/2 – 400 M = 600 MHz。由于两个通道自身的失真以及其他损伤,我们还看到了许多其他音调,但这些音调都低于–90 dB线。
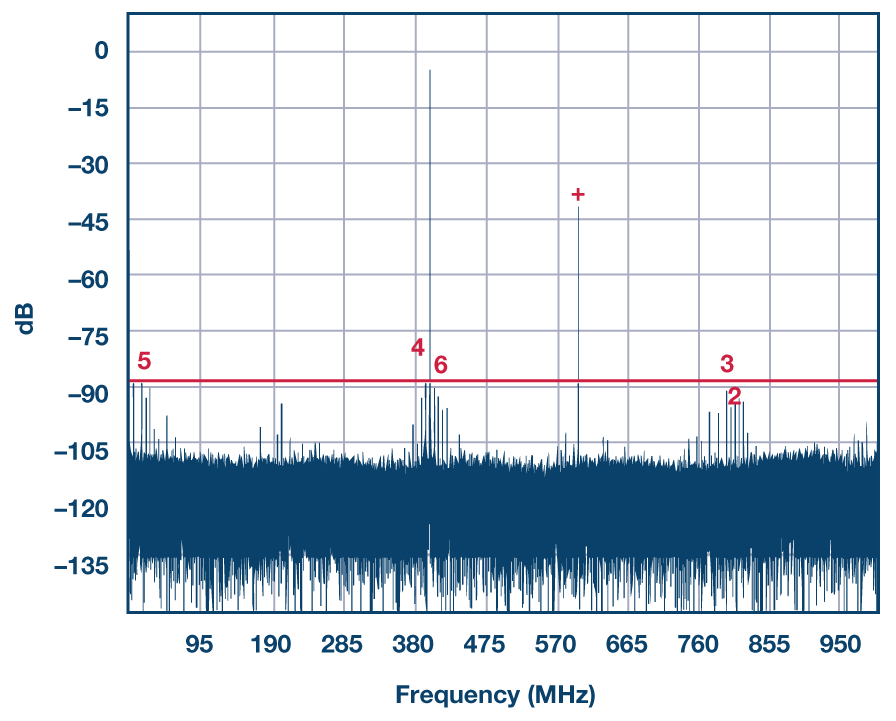
图3.乒乓球方案的2 GSPS组合输出数据频谱,方法是用1 GSPS时钟对AD9680的两个ADC进行时钟,但采样相移为180°。
高阶交错
当我们有两个以上的频道时,如上所述的频率规划不是很实用或有吸引力。交错杂散的位置不能局限于奈奎斯特带的一小部分。例如,考虑四路交错式ADC的情况,如图4(a)所示。在这种情况下,偏移失配会在直流时产生音调,fs/4和fs/2.而增益和时序交错图像位于fs/4 –f在,fs/4 +f在 和fs/2 –f在.交错式ADC输出频谱示例如图4(b)所示。可以清楚地看到,除非输入在小于fs/8,无论我们放在哪里f在,输入将与一些交错杂散重叠,如果输入是非常窄带的信号,我们不应该尝试使用宽带交错ADC对其进行数字化。
在这种情况下,我们需要最小化IL杂散功率,以获得完整的奈奎斯特和更干净的频谱。为此,使用校准技术来补偿通道之间的不匹配。随着失配的影响得到纠正,产生的IL杂散的功率降低。SFDR和SNR都受益于这种杂散功率的降低。
补偿方法受到测量和最终纠正不匹配的准确性的限制。为了进一步抑制残余杂散,使其超出通过校准达到的水平,可以间歇性和随机地打乱通道对输入进行采样的顺序。这样,前面讨论的转换输入信号由于未校准的失配而产生的调制效应从固定模式噪声变为伪随机噪声。结果,IL音调和不需要的周期性模式变成伪随机噪声样内容,随着转换器量化本底噪声的增加,并导致不需要的杂散图像和音调消失或至少传播。在这种情况下,与IL杂散成分相关的功率会增加本底噪声的功率。因此,虽然失真得到改善,但SNR会因增加噪声的IL杂散功率而降低。SNDR(SINAD)基本上没有变化,因为它结合了失真和噪声以及随机化;它只是将IL贡献从一个分量(失真)移动到另一个分量(噪声)。
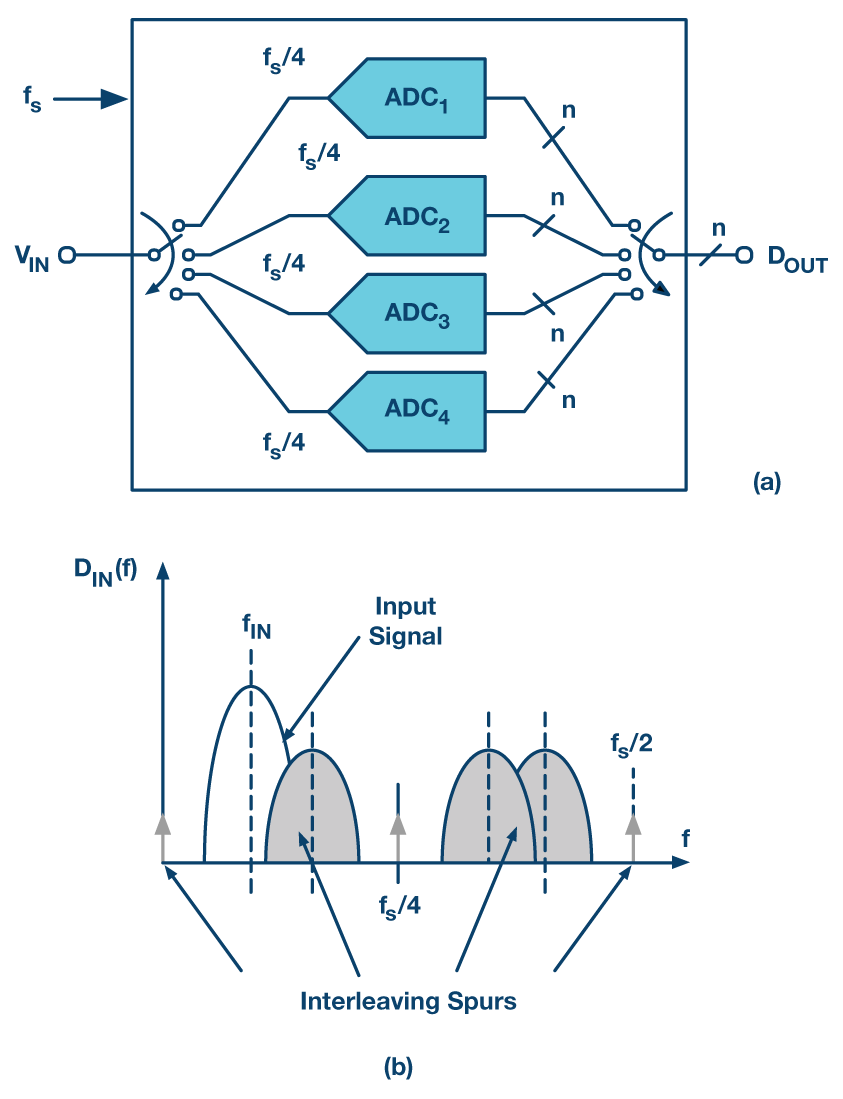
图4.(a) 四路交错式 ADC 和 (b) 相应的 1圣奈奎斯特输出频谱显示交错杂散。
我们来考虑一些交错ADC的例子。AD9625是一款12位/2.5 GSPS三路交错ADC。校准三个通道之间的失配,以尽量减少交错杂散。其输入接近1 GHz时的输出频谱示例如图5(a)所示。在此频谱中,除了 ~1 GHz 输入音调外,还可以看到通道的 2德·和 3RD500 MHz 附近的谐波失真和 4千基波附近的谐波失真。交错失配校准大大降低了交错杂散的功率,并且在整个频谱中可以看到大量额外的残余小杂散音。
为了进一步减少这种残留杂散成分,引入了信道随机化。添加第四个校准通道,然后通过间歇性地将其中一个交错通道与第四个通道交换,以随机变化的顺序对四个通道进行三路交错。人们可以把它比作一个杂耍演员在空中玩三个 Skittles,而第四个 Skittles 每隔一段时间就会换一次。这样,残余交错杂散功率被随机化并分布在本底噪声上。如图5(b)所示,通道随机化后,交错杂散几乎消失,而噪声功率略有增加,从而使SNR降低2 dB。当然,请注意,虽然图5(b)所示的第二个频谱的失真音调要干净得多,但洗牌不会影响2德·, 3RD和 4千谐波,因为这些不是交错杂散。
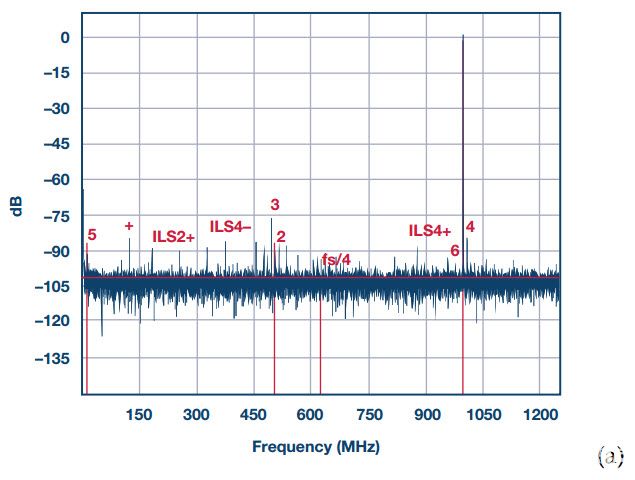
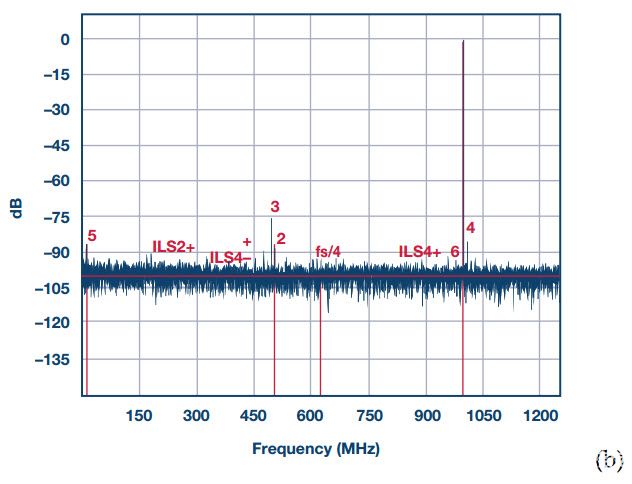
图5.AD9625的输出频谱,时钟频率为2.5 GSPS,输入音接近1 GHz。 (a) 顺序三路交错;SNR = 60 dBFS,SFDR = 72 dBc 受三次谐波的限制,接近 500 MHz;然而,在整个光谱中可以看到许多交错杂散。(b) 三向交错与随机通道洗牌;SNR = 58 dBFS,而SFDR = 72 dBc仍由三次谐波设定,所有交错杂散都已通过将其功率分散到本底噪声中而消除。
使用通道随机化的交错ADC的另一个示例是图6频谱所示。四路交错式16位/310 MSPS ADC AD9652就是这种情况。在图6所示的情况下,四个通道以固定顺序顺序交错,无需努力校准它们以减少通道失配。频谱清楚地显示了预测频率位置处的交错杂散,其大功率远大于2德·和 3RD谐波,并将无杂散动态范围限制在仅57 dBc。
但是,如果对同一ADC进行前台校准以减少通道失配,则交错杂散的功率会大大降低,如图7所示。与前面的例子类似,通道谐波失真不受影响,但是通过通道失配校准,交错杂散的功率大大降低。
最后,图7中的频谱纯度可以通过随机化通道顺序进一步提高,如图8所示。在这种情况下,随机化使用了一种专有技术,虽然间歇性地扰乱了四个通道的顺序,但不需要备用(5千) 通道,从而节省其相关功率。从图8可以看出,随机化后,所得频谱上只剩下常规谐波失真。
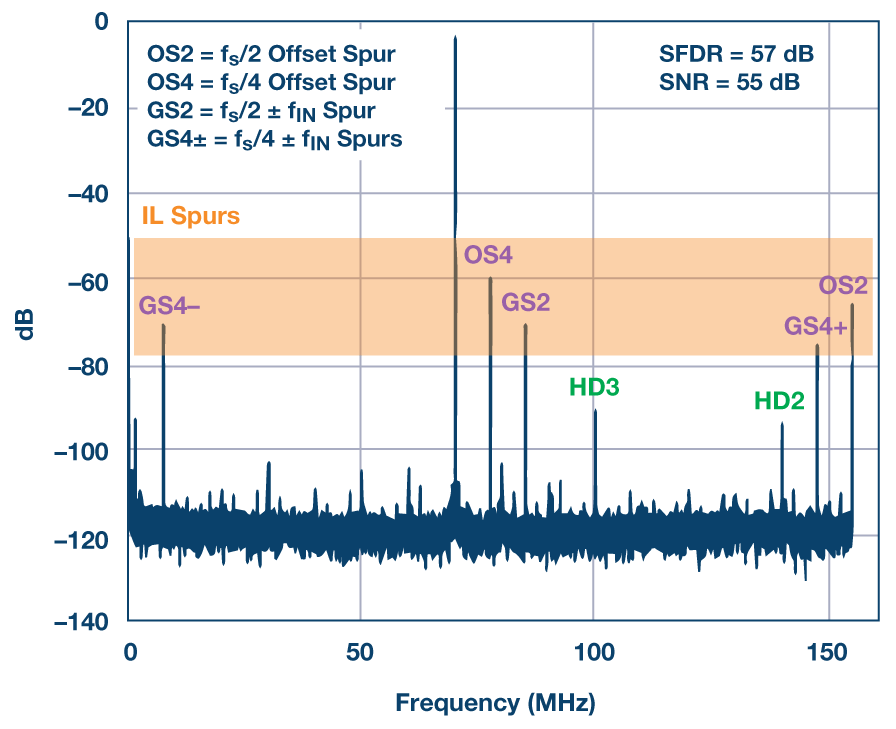
图6.AD9652的输出频谱,时钟为fs= 310 MHz,正弦输入f在~ 70 兆赫。在这种情况下,不应用通道校准和随机化。2德·(HD2) 和别名 3RD(HD3)谐波分别在~140 MHz和~100MHz处可见。交错 (IL) 杂散也可见。这些是直流时的偏移音,fs/2(图中的 OS2)和fs/4(图中的OS4)。此外,增益(/时序)杂散可以在fs/2 –f在(图中GS2),fs/4 +f在(图中的GS4+)和fs/4 –f在(图中的GS4)。此图中的SNR报价人为地较差,因为某些杂散成分与噪声功率混为一谈。
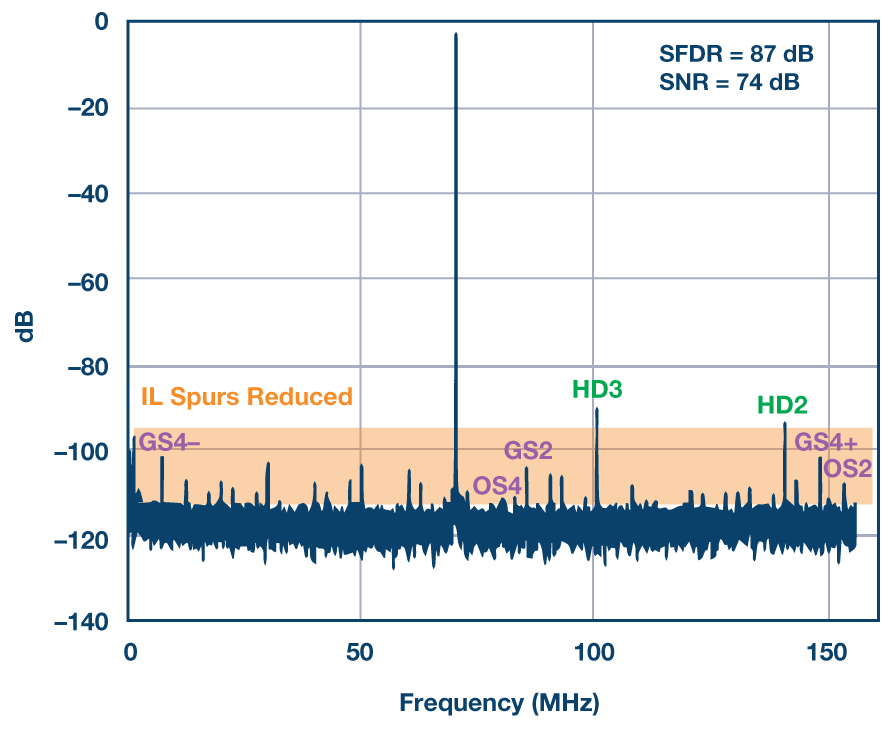
图7.相同AD9652的输出频谱,输入相同,但经过校准后,四个通道以减少其失配。与图6相比,而2德·和 3RD谐波不受影响,交错杂散的功率大幅降低,SFDR从57 dBc提高到87 dBc,提高了30 dB。
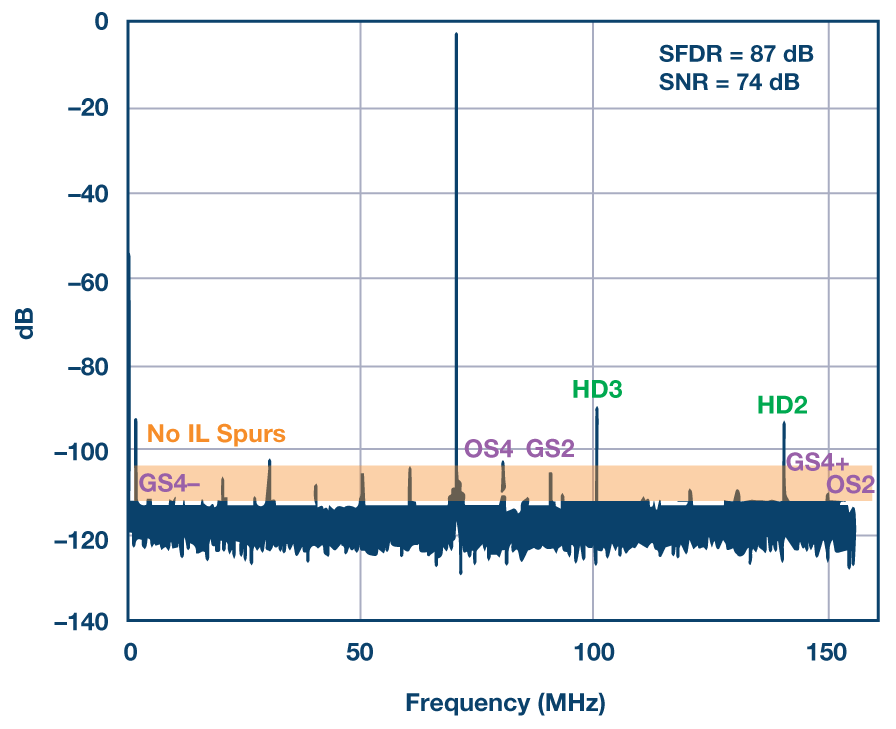
图8.打开交错顺序随机化后前一种情况的输出频谱。对残余交错杂散进行随机化,将其功率分布到本底噪声上,相应的峰值消失。只剩下常规的谐波失真。SNR几乎不受影响,因为在失配校准后,交错音的分布式杂散功率可以忽略不计。
结论
时间交错是增加数据转换器带宽的强大技术。失配补偿以及通过随机化技术消除残余杂散成分的最新进展使得超高速12位、14位和16位交错ADC得以完全集成。
在输入信号受频带限制的情况下,例如在许多通信应用中,乒乓(双向)交错方法允许通过频率规划将不需要的交错杂散从目标输入频带中分配出来。然后可以对虚假内容进行数字过滤。与非交错式ADC相比,这种方法消耗的功耗大约是捕获相同无杂散输入带宽所需的IL采样速率的两倍,但另一方面,由于IL采样速率较高,该方法既通过处理增益将动态范围增加了3 dB,又放宽了ADC之前的抗混叠和屋顶滤波器的滚降。
当需要IL转换器的全输入频段来捕获宽带输入信号时,适合使用高阶交错转换器。在这种情况下,校准和随机洗牌允许交错失真和杂散内容补偿和消除。
审核编辑:郭婷
-
转换器
+关注
关注
27文章
8653浏览量
146944 -
数据转换器
+关注
关注
1文章
359浏览量
27990
发布评论请先 登录
相关推荐
交错式ADC的基础知识
基于时间交错技术实现10位/400 MSPS ADC的设计
一文了解交错式ADC(数据转换器)
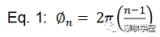
详解时间交错技术
交错ADC之间的增益不匹配
拓展一些关于交错ADC的观点
天文学家揭开快速射电暴的谜团
一文详细了解ADC时间交错技术
交错式ADC:基础知识
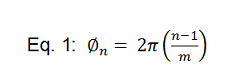




 交错ADC:揭开谜团
交错ADC:揭开谜团
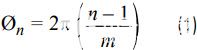










评论