MEMS IMU/陀螺仪对准的基础知识

传感器未对准通常是在其反馈回路中使用MEMS惯性测量单元（IMU）的高性能运动控制系统的关键考虑因素。对于IMU中的陀螺仪，传感器未对准描述了每个陀螺仪的旋转轴与系统定义的惯性参考系（也称为全局系）之间的角度差。管理未对准对传感器精度的影响可能需要独特的封装、特殊的装配工艺，甚至是最终配置中的复杂惯性测试。所有这些都会对重要的项目管理指标产生重大影响，例如进度、投资以及与每个系统中的 IMU 相关的总成本。因此，传感器对准是设计周期早期阶段需要考虑的指标，同时有时间围绕最有效的解决方案定义系统架构。毕竟，没有人愿意花掉80%的项目进度和预算来发现他们廉价的传感器需要数百甚至数千美元的意外成本加法器来满足最终用户不可协商的可交付成果。哎哟！

在为系统构建 IMU 功能时，需要了解和评估三个基本对准概念：误差估计、了解未对准对关键系统行为的影响以及电子对准（安装后）。初始误差估计应包括来自 IMU 和在运行期间将其固定到位的机械系统的误差贡献。了解这些错误对系统关键功能的影响有助于建立相关的性能目标，防止问题过度工作，同时管理错过关键性能和成本承诺的风险。最后，某种形式的电子对齐对于优化系统的性能/成本交易空间可能是必要的。

预测安装后的对齐误差

应用中的对准精度将取决于两个关键因素：IMU的对准误差和在操作过程中将其固定到位的机械系统的精度。乌兹别克斯坦伊斯兰运动的贡献（Ψ模压组）和系统的贡献（Ψ.SYS） 通常彼此不相关，因此估计总错位误差通常来自使用和方根计算将这两个误差源组合在一起：

一些 IMU 规格表通过轴到封装未对准误差或轴到帧未对准误差等参数来量化未对准误差。图1提供了ADIS16485中每个陀螺仪相对于其封装边缘的这些未对准误差的夸大视图。在此图中，绿色虚线表示包定义的参考系中的轴。实线表示封装内陀螺仪的旋转轴和 Ψ模压组表示三个错位项的最大值 （ΨX, ΨY, ΨZ).

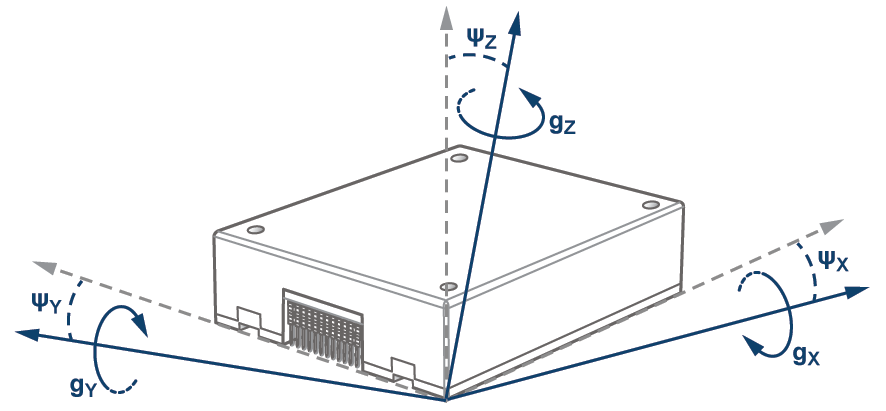
图1.ADIS16485轴帧未对准。

预测系统的贡献（Ψ.SYS在公式1中，未对准误差涉及分析任何机械缺陷的机会，这些缺陷可能会使IMU相对于全局框架在系统中的静止位置倾斜。使用焊接到印刷电路板的 IMU 时，这将涉及考虑原始放置精度、焊料沉积变化、焊料回流期间的浮子、关键 PCB 功能（如安装孔）的公差以及系统框架本身的公差。使用模块级IMU时，可以更直接地耦合到系统机箱，如图2所示。这种类型的接口具有两个关键的机械功能，有助于管理安装倾斜错误、安装壁架 （4×） 和安装套。

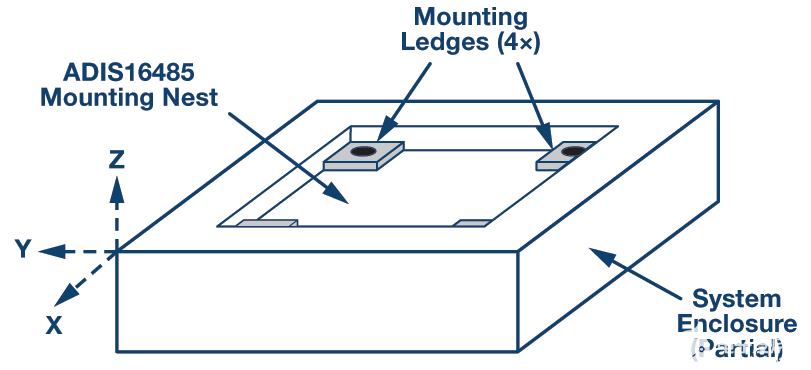
图2.嵌套底板设计理念。

在这种类型的安装方案中，四个安装壁架的高度变化是机械变化的一个例子，它可能导致 x 轴和 y 轴上的安装倾斜。图3提供了一个夸张的图示，以帮助解释这种变化（H1与H2）对安装偏斜（ΨX），相对于 x 轴。

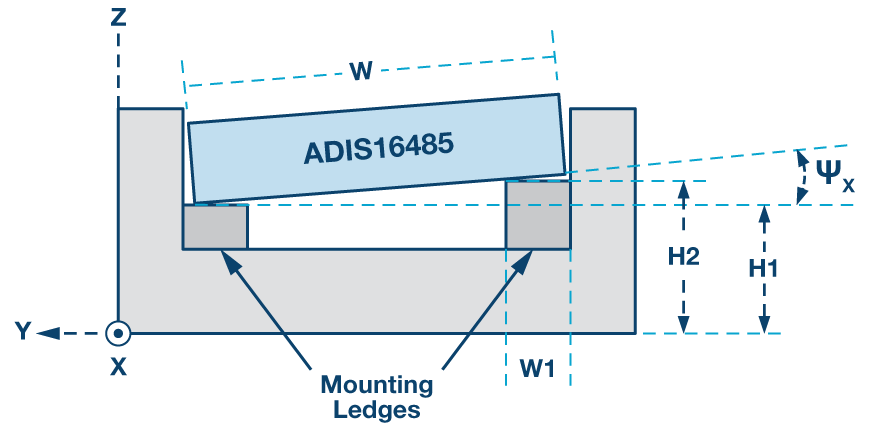
图3.由于安装壁架变化而导致的未对准误差。

公式2提供了用于预测x轴偏斜角（ΨX）与高度差（H2 到 H1）和两个接触点之间的跨度（W 到 W1）相关：

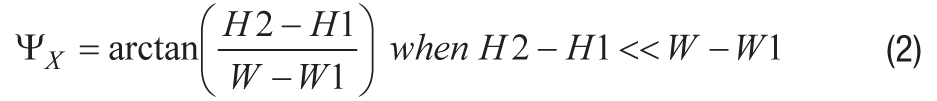
安装壁架高度的变化将对围绕 y 轴的安装倾斜产生类似的影响。在这种情况下，用封装长度（L）代替公式2中的宽度（W），以建立以下关系，用于估计y轴倾斜角（ΨY).

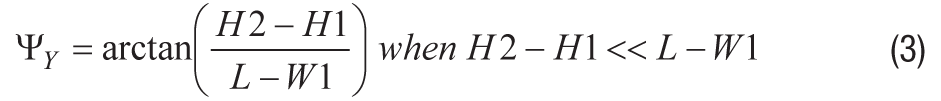
图 4 提供了另一个示例，说明机械属性如何影响围绕 z 轴的安装倾斜。在这种情况下，机器螺钉将滑过 IMU 主体上的安装孔（所有四个角），穿过安装壁架上的孔，然后滑入安装壁架背面的锁紧螺母中。在这种情况下，机床螺钉 （DM） 的直径与其在底板上的相关直通孔 （DH） 之间的差异会导致 z 轴出现歪斜。

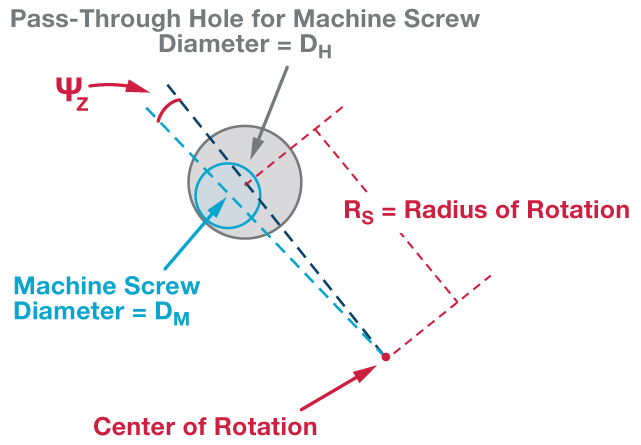
图4.安装螺钉/孔对 z 轴倾斜角度的影响。

公式4提供了预测z轴安装倾斜机会（ΨZ），基于直径和旋转半径的差异（RS），等于相对角上两个安装螺钉之间距离的一半。

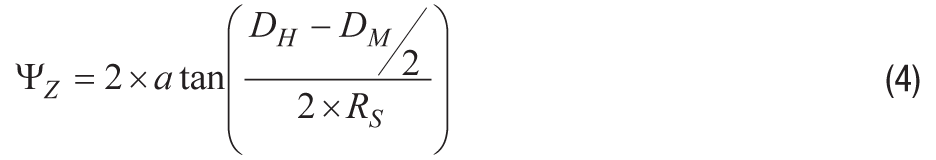
例 1

估算使用2 mm机械螺钉将ADIS16485安装到6 mm×6 mm安装壁架上的总体误差，这些壁架具有2.85 mm孔，高度公差为0.2 mm。

溶液

使用44 mm的标称宽度（W），x轴偏斜角（见图3）预测为0.3°。

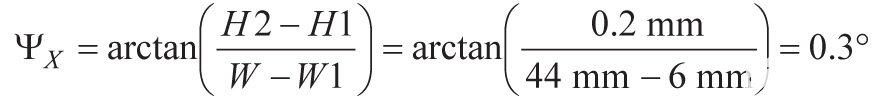
该封装两侧安装孔之间的标称距离分别为 39.6 mm 和 42.6 mm。这些尺寸形成直角三角形的两侧，其斜边等于包装相对角的两个孔之间的距离。旋转半径 （RS，参见图 4）等于该距离的一半 （29.1 mm），这导致预测 z 轴上的偏斜为 0.83°。

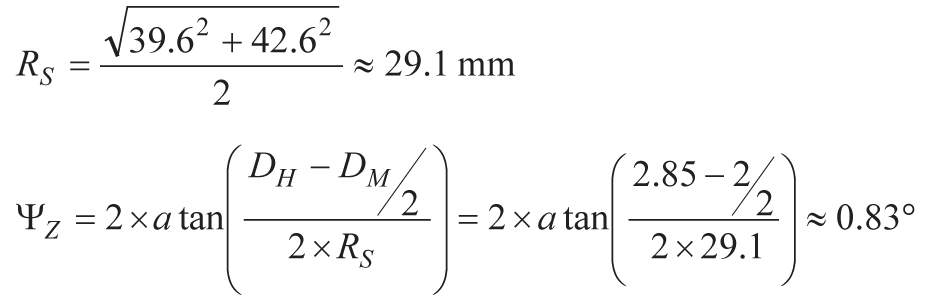
对于公式1中的复合预测公式，Ψ.SYS等于 ΨZ（估计值的最大值）和 Ψ模压组等于 1°，根据 IMU 数据手册中的轴到帧未对准误差规范。这将产生1.28°的总对准误差估计值。

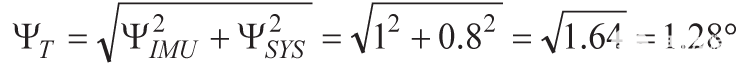
未对准对系统精度的影响

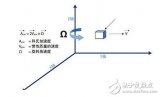
在为应用开发精度标准时，了解未对准误差及其对陀螺仪精度的影响之间的基本关系是一个很好的起点。为了开始此过程，图5提供了三轴陀螺仪系统的通用图示。在此图中，三条绿色实线表示全局框架中的三个轴，黑色实线表示所有三个陀螺仪的旋转轴，基于 Ψ 的标签表示全局框架和陀螺仪轴之间的未对准误差。等式5、等式6和等式7展示了对准误差对每个陀螺仪在全局坐标系中绕其指定轴旋转的响应的影响。在这些方程中，未对准角的余弦值引入了刻度误差。

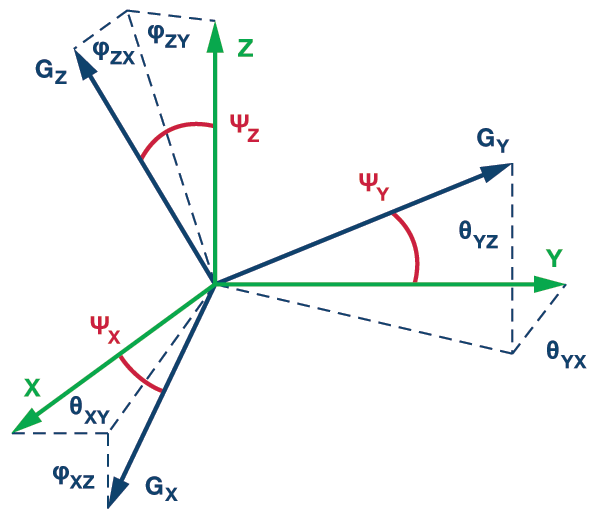
图5.具有对准误差的正交三轴陀螺仪。

未对准误差还会在每个轴上引入跨轴影响。量化这些影响需要将每个轴的未对准角度分解为两个分量，这两个分量与其他两个轴相关。例如，ΨX具有 y 轴组件 （φ扎伊） 和 z 轴组件 （φXZ），这导致 x 轴陀螺仪对全局坐标系中围绕所有三个轴旋转的响应展开如下 （ωX1 吨Y1 吨Z):

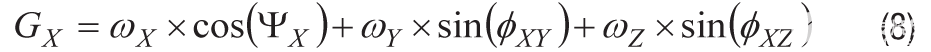
同样的扩展适用于 y 轴和 z 轴陀螺仪：

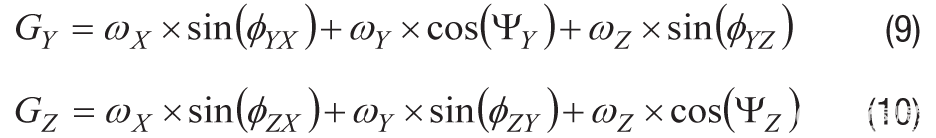
对等式8、等式9和等式10的两侧进行积分会产生类似的关系，即角度位移。在得到的公式11、公式12和公式13中，感兴趣角是围绕全局框架的角位移（θXω, θYω, θZω）和每个陀螺仪的积分（θXG, θ永格, θZG).

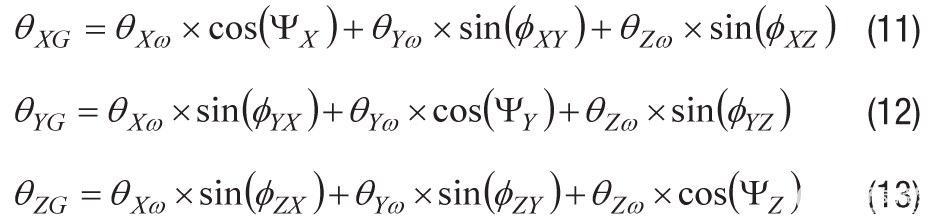
例 2

地面无人驾驶车辆（UV）正在使用MEMS IMU作为其天线的平台稳定控制（PSC）系统中的反馈传感器。该系统采用RSS调谐器环路，要求方位角和仰角保持在±1°以保持连续通信。在最动态的条件下，PSC 严重依赖 y 轴陀螺仪的测量进行仰角控制，并依赖 z 轴陀螺仪的测量进行方位角控制。在这些动态条件下，航向 （θZω） 的最大变化为 30°，并且没有围绕 x 轴或 y 轴 （θXω= θYω= 0） 在此操作期间。

溶液

围绕x轴和y轴的零旋转使公式8和公式9减少到如下：

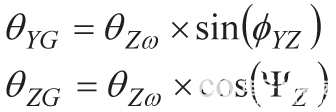
从 y 轴开始，为 θ 建立 1° 的最大边界永格并求解错位项 ΦYZ.该过程为y轴陀螺仪建立了1.9°的最大允许对准误差。

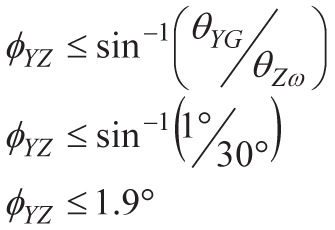
对于 z 轴，设置 θZω等于 30° 并建立 1° 的最大边界，对于 θ 之间的差值ZG和 θZω，然后求解 ΨZ.此过程在z轴陀螺仪上建立了14.8°的最大允许对准误差。

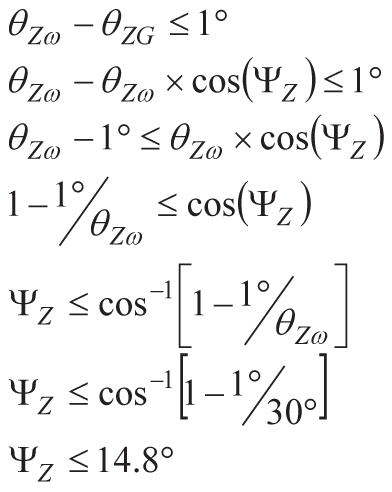
这些计算表明，对于这种特定的机动/场景，y轴和z轴之间的交叉轴行为将驱动~1.9°的对准精度要求。

电子对准

在 IMU 和附件系统无法满足关键系统目标的情况下，电子对准提供了一种减少错位误差的方法。此过程有两个关键步骤：表征未对准项（在IMU安装后）并开发一个校正对准矩阵，该矩阵校正陀螺仪，使其在应用于陀螺仪阵列时响应，就好像它们与全局帧对齐一样。公式14为此过程提供了一个系统模型，其中围绕全局帧中每个轴的旋转（ω）是三个系统输入，三个陀螺仪响应（G）是系统输出，3×3矩阵（M）表示输入和输出之间的系统行为（包括未对准）。

简单的代数操作确定陀螺仪测量值（G）和M（M）的倒数的乘积–1） 等于全局帧的旋转数组 （ω）。因此，对齐矩阵等于 M–1.

等式8、等式9和等式10为扩展等式14提供了基础，以包括等式16中的未对准项，以及等式17和等式18中的更一般的未对准项：

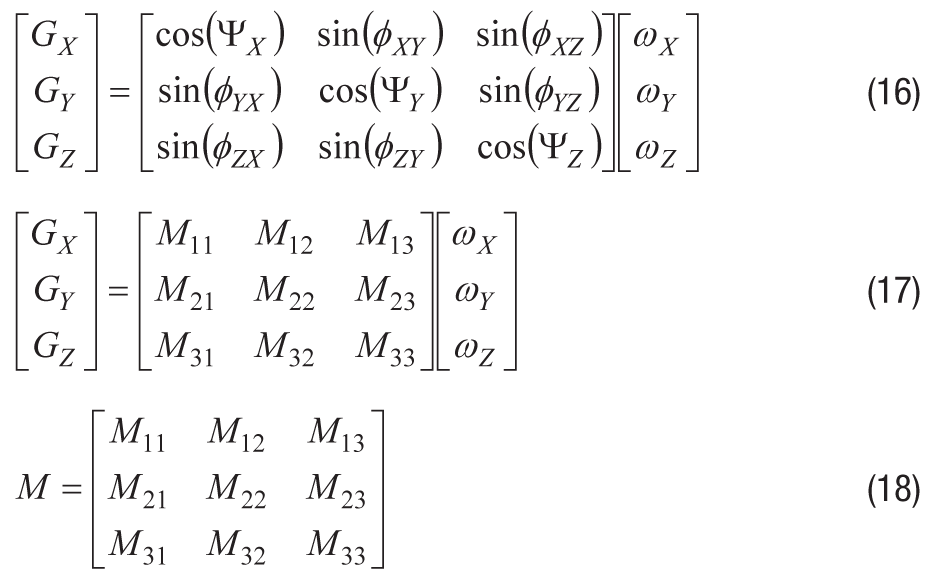
一次围绕一个轴旋转整个系统可以简化系统模型，足以将矩阵中的每个元件与陀螺仪测量值隔离开来。例如，围绕 x 轴旋转系统（ωX= ωTR<> 吨Y= 0, ωZ= 0），同时观察所有三个陀螺仪有助于将 M11、M21 和 M31 的关系简化为以下内容：

使用相同的方法，y 轴旋转 （ωX= 0, ωY= ωTR<> 吨Z= 0） 有助于将 M12、M22 和 M32 的关系简化为以下内容：

最后，z轴旋转（ωX= 0, ωY= 0, ωZ= ωTR） 有助于将 M13、M23 和 M33 的关系简化为以下内容：

显然，运动曲线（ω）和陀螺仪测量（G）的精度对这一过程有直接影响。特别是，离轴运动会对这一过程产生重大影响，因此在购买和部署将执行这些要求的惯性测试设备时，应该强烈考虑这一点。关于陀螺仪的精度，偏置和噪声是精度的两个威胁，在此过程中通常需要考虑。一种管理残余偏置误差影响的技术（bE）在陀螺仪测量中通过使用两种不同的旋转速率，它们彼此相等且相反。例如，当绕 y 轴沿正方向旋转 （ωY= ωTR<> 吨X= ωZ= 0），公式28描述了z轴陀螺仪响应，具有偏置误差。公式29描述了在负方向上绕y轴旋转时z轴陀螺仪响应（ωY= –ωTR<> 吨X= ωZ= 0）：

重新排列公式29以与偏置误差（bE），将其代入公式28，然后求解M32。注意偏置误差（bE） 从公式中掉出。

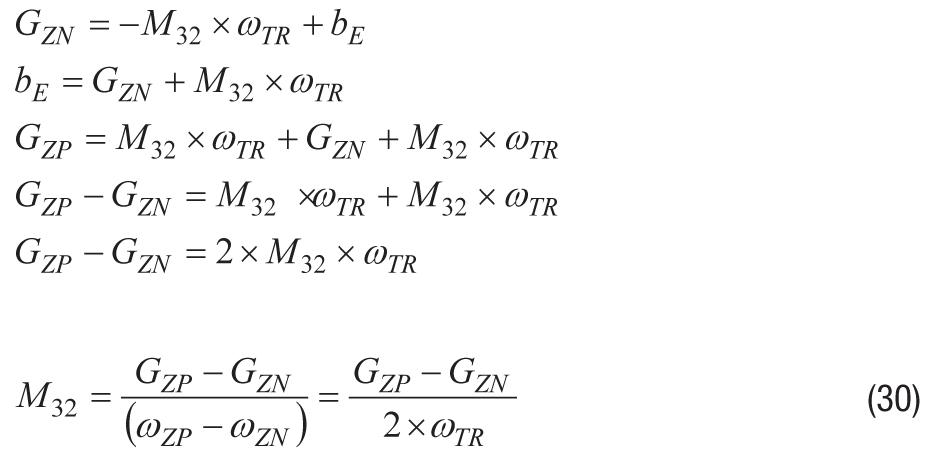
该公式假设在两次测量期间偏置误差都是恒定的，这不是一个现实的期望，因此明智的做法是了解测量之间变化的机会（温度、时间和噪声）。当连续进行测量时，在稳定的温度条件下，噪声通常是在此过程中需要管理的关键误差。陀螺仪测量中可接受的噪声水平将取决于对准精度目标（ΨT）和表征过程中每个轴上的旋转速率（ωTR).一种常见的降噪技术是在惯性条件恒定的情况下对陀螺仪数据的时间记录求平均值。艾伦方差曲线提供了一种工具，用于理解重复性（噪声）和平均时间之间的权衡。

例 3

如果检定期间的旋转速率为100°/s，对准精度目标为0.1°，噪声（rms）必须比未对准目标小10×，则需要ADIS16485的平均输出多长时间才能实现这些目标？

溶液

使用陀螺仪和输入之间的通用响应（在测试平台上旋转），以下计算表明每个陀螺仪中的总噪声（rms）必须小于62°/小时。

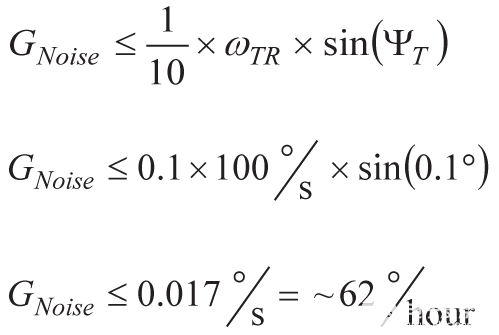
图 6 提供了一个示例，说明如何使用此 IMU 的艾伦方差曲线来选择满足此要求的平均时间。在这种情况下，0.1 秒的平均时间符合 62°/小时的可重复性目标，并具有一定的余量。

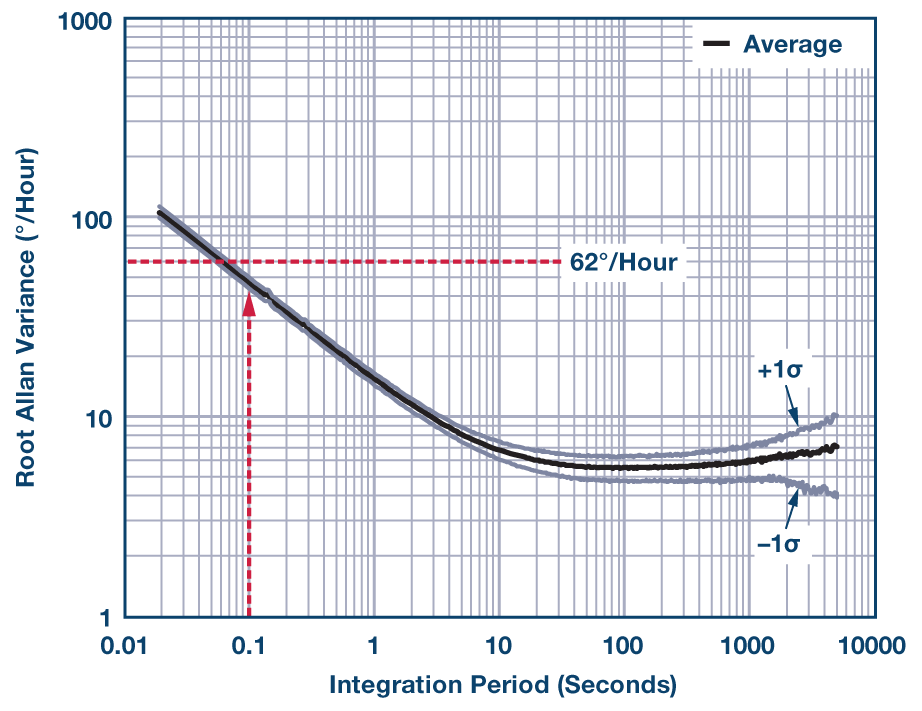
图6.ADIS16485 艾伦方差曲线。

请注意，这种方法仅考虑传感器本身的噪声。如果测试平台的振动增加了陀螺仪测量的噪声，则可能需要额外的考虑和过滤。

简化流程的提示和技巧

开发具有必要精度和环境控制温度的三轴惯性测试系统通常需要在资本设备和工程开发资源方面进行大量投资。对于那些正在开发第一代或第二代系统的人来说，在开发过程中有很多问题需要回答，这些类型的资源或时间可能不可用。这种情况需要一种更简单的解决方案，这可以通过仔细选择IMU并利用仪器或应用中可用的自然运动来实现。

例如，有时使用角度可能比使用角速率测量更方便。等式31结合了等式11、等式12和等式13，以围绕全局帧的角度表示系统行为（M）（θXω, θYω, θZω）和积分陀螺仪输出（θXG, θ永格, θZG):

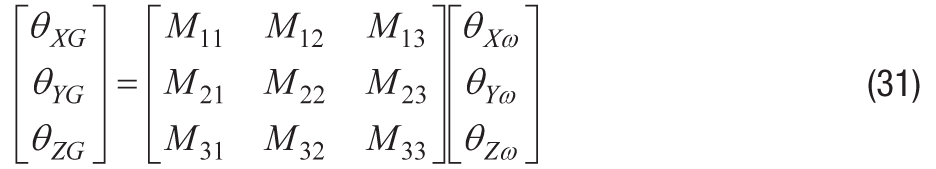
在器件选择方面，轴间未对准误差是需要考虑的关键参数，因为当它低于轴到封装未对准参数时，它有助于降低与电子对准相关的惯性测试曲线（在公式16中）的复杂性。虽然轴到封装未对准参数描述陀螺仪方向，但相对于外部机械参考，轴到轴未对准参数将每个陀螺仪相对于其他两个陀螺仪的方向相关联。大多数情况下，MEMS IMU中三个陀螺仪的理想方向是彼此相距90°，因此轴到轴的未对准与这种行为的另一个常见参数有关 - 交叉轴灵敏度。使用图 7 作为参考，轴到轴的未对准将表示以下三种关系中的最大值：

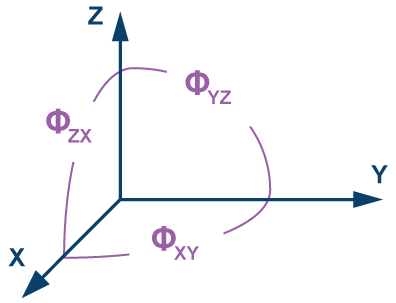
图7.轴到轴未对准图。

轴到轴未对准参数确定与在开发电子对准过程时假设传感器具有完美的正交对准相关的误差。使用完全正交假设，人们只能通过两个旋转轴对齐所有三个轴。例如，绕 y 轴和 z 轴旋转可直接观察 M12、M13、M22、M23、M32 和 M33。假设完全正交对齐并应用一些三角函数属性，可以使用六个元素和以下关系计算其他三个元素（M11、M21 和 M31）：

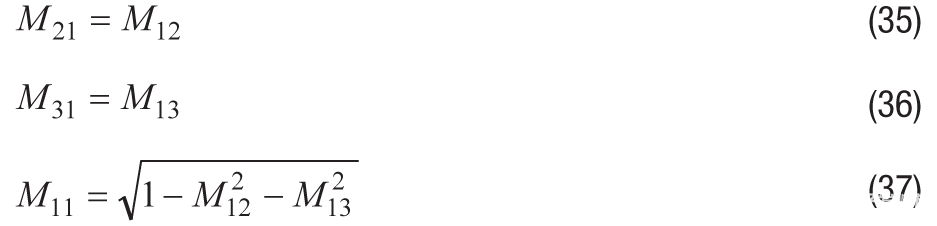
这些标识会导致对系统模型的以下更新，其中 M 矩阵中的所有九个元素都是来自 y 轴和 z 轴旋转的六个元素。

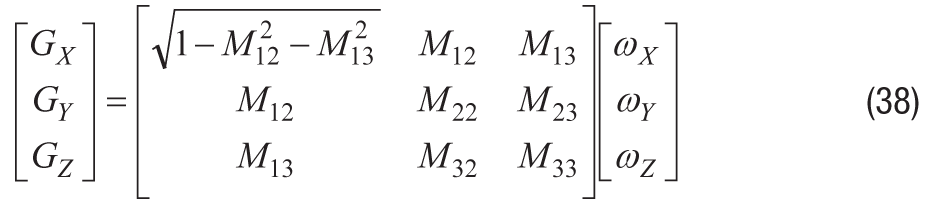
结论

惯性MEMS技术在过去几年中取得了惊人的进步，在复杂的贸易空间中为系统开发人员提供了广泛的选择，包括尺寸、重量、功耗、单位成本、集成成本和性能。对于那些第一次使用MEMS IMU构建运动控制系统的人来说，在选择合适的IMU和准备使用此IMU支持关键系统要求方面，有很多东西需要学习。由于对准精度会对关键性能、成本和进度目标产生重大影响，因此这是一个重要的考虑因素。即使是简单的分析工具也有助于在概念和架构设计阶段识别潜在风险项目，同时仍有时间影响器件选择、机械设计、装配后校准（电子校准）、初步成本预测和关键进度里程碑。更进一步，其他人将发现识别MEMS IMU关键指标和机会的价值，以用系统中可用的自然运动替换三轴惯性测试设备，从而从其系统中获得最佳价值（性能，总部署成本）。

审核编辑：郭婷