逻辑功能的门级实现受门扇入的限制。本文探讨了逻辑分解、分组和电平增加,以在有限的输入门下实现逻辑功能。
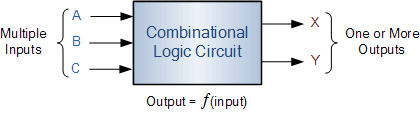
了解如何利用 组合逻辑功能 并简化组合逻辑电路!为了理解与这些过程相关的挑战,让我们首先建立一个真实世界的例子来演示这个概念。
为什么栅极输入的数量有限?
想象一下,我们正在设计一个逻辑系统,以便在六个紧急出口中的任何一个打开时启动警报信号(S)。报警系统的输出通常为高电平(逻辑 1),并通过变低(逻辑
0)来启动报警。门传感器(标记为 a 到 f)在关闭时分别输出逻辑 0,打开时输出逻辑 1。
我们可以很容易地将此逻辑函数表示为:
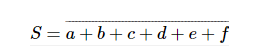
在具有六输入NOR门的单级逻辑功能中实现这一点非常简单。从理论上讲,我们可以扩展图1所示的双输入NOR门的设计,以支持所需的6个输入。

图1. CMOS 2 输入 NOR 栅极
六个并联的NMOS晶体管不一定是问题。然而,由于电源电压有限(V日嘎)。因此,基本逻辑门通常限制为某个最大输入数(通常为四个)。逻辑门的输入数量称为扇入。
使用具有有限输入的门进行分组设计
对于我们的报警系统问题,我们可以对输入进行分组和因子分解,以允许我们使用门实现组合电路设计,每个门最多有三个输入。对于低压逻辑过程来说,这是一个更合理的扇入。
实现此目的的一种可能的分解是:

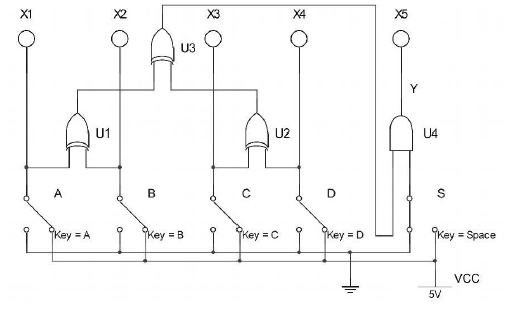
这里的结果是一个两电平逻辑系统,如图2所示,其中所有三个门最多有三个输入。

图2. 报警系统的门级逻辑限制为最多 3 个输入门
实现具有有限扇入的复杂逻辑功能
对于更复杂的逻辑功能,可以根据需要重复分解、重新分组和增加逻辑电平数的过程,直到所有门都达到所用逻辑技术的最大扇入限制。
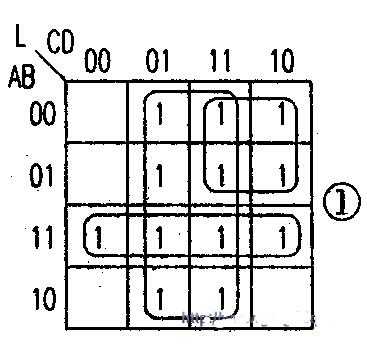
让我们仔细看看一个更复杂的逻辑函数,由 卡诺地图 图3。

图3. 卡诺地图
我们可以通过对相邻 1 的项进行分组,从 Karnaugh 映射中推导出逻辑方程。首先,我们可以对顶行进行分组,如图 4 所示。

图4. 卡诺地图的术语分组
对于顶行,我们可以将部分逻辑函数导出为:

类似地,我们可以创建相邻 1 项的四个附加分组,如图 5 所示。

图5. 卡诺地图的附加术语分组
对于这四个分组,我们可以推导出逻辑函数的其余项:

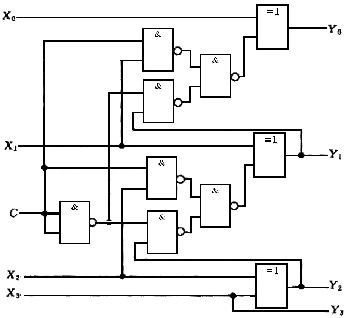
此功能现在可以通过最大扇入为三个的门来实现。由此产生的门级逻辑功能如图6所示。

图6. 用于逻辑功能的门级逻辑限制为最大三输入门
门级逻辑综合
在现代数字集成电路设计中,最常见的是,逻辑功能转换为门级实现将通过门级逻辑合成过程执行。数字标准单元逻辑库将具有一套逻辑门,用于在硬件中创建所需的功能。电子设计自动化(EDA)软件将转换以更高级语言描述的逻辑功能,例如
威瑞洛格 变成仅使用库中可用的门的物理门级实现。
标准单元库中可用栅极的扇入将受到目标半导体工艺以及电压和温度工作条件的限制。因此,EDA
软件必须执行本文中所述逻辑电平数的分解、重新分组和增加。
门级逻辑仿真
在理想的逻辑仿真中,输出会随着输入的任何变化而瞬时变化。在实际系统中,存在“传播延迟”,因为输入电压变化通过电路中的晶体管传播以引起输出电压的变化。输出负载以及输入和输出信号的上升和下降时间也会影响整个电路信号的传播特性。
时序图
让我们看一下逆变器时序图的简单示例,如图7所示。当输入 x 改变逻辑状态时,输出在延迟后会发生变化。
在本例中,下降输出传播延迟df比上升输出传播延迟dr更短,斜率更陡。延迟在两个逻辑电平之间的50%电平上测量。这种类型的不对称响应将发生在CMOS逆变器中,其中NMOS和PMOS晶体管尺寸相同。NMOS晶体管的较高驱动电流将比PMOS晶体管拉高输出的速度更快。

图7. 逆变器的时序图
时序图还可用于评估具有多个输入和门的逻辑电路。在图8的示例电路中,输入端的变化 一个 通过第一个 NAND 门传播到输出 x 具有输入至输出传播延迟
d.

图8. 多电平逻辑电路的时序图
值的变化 x 然后通过第二个 NAND 门传播到输出 y 具有额外的传播延迟 d。因此,总传播延迟从 一个 自 y 为 2d.
-
电路设计
+关注
关注
6673文章
2451浏览量
204168 -
仿真
+关注
关注
50文章
4071浏览量
133552 -
逻辑
+关注
关注
2文章
833浏览量
29464
发布评论请先 登录
相关推荐
组合逻辑电路的分析与设计-逻辑代数

基于组合逻辑电路实现方法的探究
Multisim在组合逻辑电路设计中的常用元件和详细作用分析
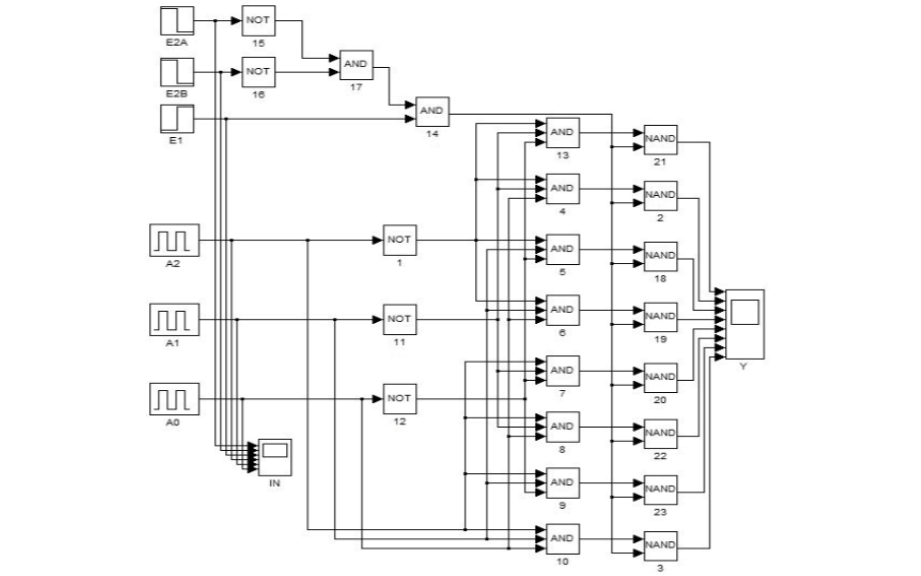
使用Matlab实现组合逻辑电路的设计与仿真




 使用栅极的组合逻辑电路设计和仿真
使用栅极的组合逻辑电路设计和仿真










评论