本文讨论运算放大器的直流限制及其影响,包括输入偏置电流、输入失调电压、CMRR、PSRR和输入阻抗。本文将使读者更好地了解这些限制如何在高精度应用中产生精度问题。
运算放大器是双端口集成电路(IC),它们对外部输入信号施加精确的增益,并提供放大后的输出:输入×闭环增益。精密运算放大器在低至中等频率和中等直流增益下工作时表现接近理想。然而,即使在这些条件下,运算放大器性能也会受到其他因素的影响,这些因素会影响精度并限制性能。在这些限制中,最常见的是高直流增益应用中占主导地位的折合到输入端的误差。
本文将讨论折合到输入端的误差对运算放大器的影响。这些误差包括输入偏置电流、输入失调电流、输入失调电压、CMRR、PSRR和有限输入阻抗。实际上,所有这些错误将同时发生。我们还解释了为什么设计人员应该警惕数据手册EC表中描述的运算放大器性能规格仅在该表顶部定义的条件下得到保证,除非另有说明的特定特性。实际上,当电源电压、共模电压范围和其他条件发生变化时,这些直流误差的影响会发生变化。
输入偏置和输入失调电流引起的误差
我们都熟悉我们周围的潜在危险,我们工程师往往会忘记在设计时也有危险的陷阱需要避免。让我们看看这对运算放大器有何影响。
我们从两个基本等式开始:
IB = (IBP + IBN)/2 …..
IOS = IBP - IBN …..
哪里:
IB是流入输入引脚的平均输入偏置电流;
IBP 是流入正输入端的输入偏置电流;
IBN是流入负输入的输入偏置电流;
IOS是输入失调电流。
输入偏置和输入失调电流是许多精密放大器应用中两个最关键的特性;它们通过阻性和容性反馈影响输出。许多反相、同相、求和和差分放大器在其有源输入设置为零后降至图2A和2B。对于此分析,我们将所有输入信号设置为零,以评估输入电流对输出精度的影响。我们将分别分析阻性反馈(图2A)和电容反馈(图2B)电路。
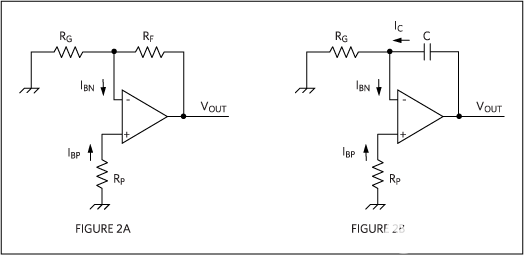
图 2A.带阻性反馈的运算放大器。图 2B.带电容反馈的运算放大器。示例器件包括MAX9620和MAX4238运算放大器。
应用图 2A 上的叠加定理可得到:
VOUT = (1 + RF/RG) × [(RF//RG) × IBN – RP × IBP] ……
从公式3可以得出以下推论:
在没有任何输入信号的情况下,电路产生有限的输出电压。这种不需要的输出误差也称为输出直流噪声。
输出电压通过将输入误差或输入直流噪声放大(1 + R)产生FRG).
输入直流噪声有两个分量:压降为I英国石油公司流经 RP和电压降,因为我亿流经 R 的组合FRG.
根据应用中所需的精度水平,我们必须对无源元件值和运算放大器本身做出一些谨慎的选择。这是消除输入偏置电流对输出精度影响的最佳方法。因此,选择 RP= RFRG收益 率:
VOUT = - (1 + RF/RG) × (RF//RG) × IOS …..
选择 RP= RFRG帮助我们减少数量级的输出误差。但对于传感器接口具有大增益(> 100V/V)的高精度应用,仍然最好选择低输入失调电流运算放大器。此外,添加 R 并不总是可行的P.最后,输入偏置电流和电阻大小在输出误差中起着重要作用。针对这些情况,设计人员应选择具有低输入偏置电流、低输入失调电压、低速度功率比以及高CMRR和PSRR的运算放大器,如MAX44260、MAX9620和MAX4238。
通过选择较低的R可以进一步降低输出误差F和 RG这反过来又增加了电路的功耗。在选择电阻尺寸时,需要在输出误差和功耗之间保持谨慎的权衡。
现在我们回到图 2B。正输入和负输入上的电压产生:
VIN+ = VIN- = -RP × IBP
其中 VHNJ是同相输入端的电压,V在-是反相输入端的电压。
应用基尔霍夫关于反转输入收益率的现行定律:
VIN-/RG + IBN - IC = 0…..
我们消除V在-在公式6中,用公式5代入,公式7得到输入偏置电流和通过反馈电容的电流:
IC = (RG × IBN - RP × IBP)/RG …..
现在应用迈克尔法拉第电容定律:
VC = 1/C ƒIC dt
其中 VC是电容器两端的电压,也是 V外.将等式7代入等式8得到:
VOUT = 1/(RG × C) × Integral(RG × IBN - RP × IBP)dt…..
公式9给出了图2B中的输出电压误差。若要最大程度地减少此错误,可以选择 RP= RG,这将公式 9 简化为:
VOUT = -1/(C) × Integral(IOS) dt …..
由于 C 和IOS相对恒定,随时间推移对公式10进行积分将得到:
VOUT = -IOS × t/C …….
等式11表示一个电压斜坡,驱动运算放大器达到饱和状态。
V 引起的错误操作系统和TCV操作系统
1
现在,我们将解释输入失调电压对运算放大器电路中典型阻性和容性反馈的影响。

图 3A.带阻性反馈的运算放大器。图 3B.带电容反馈的运算放大器。
从图3A可以看出,输出电压误差为:
VOUT = (1 + RF/RG) × VOS …..
其中 (1 + RF/RG) 是直流噪声增益。电阻越大,误差越大。
从图 3B 中,我们有 IC= IRG,用于输入偏置电流可忽略不计的运算放大器;对于 V在-= V操作系统,我们有我C= IRG = V操作系统/RG.使用法拉第电容定律可得到:
VOUT = Integral(VOS) dt/(RG × C) …..
同样,如果我们随着时间的推移对公式13进行积分,运算放大器输出会饱和到任一电源轨,具体取决于V的极性。操作系统.
从公式12和13可以得出一个重要结论:对于给定的无源电阻和电容值,失调电压是累积输出电压误差的主要因素。
现在是举个例子的时候了。失调电压(TCVos)和输入失调电压的热漂移在温度变化常见的精密应用中起着非常关键的作用。强调TCV的重要性操作系统对于精密应用中的运算放大器,我们比较了典型运算放大器(最大TCV操作系统= 5μV/°C 和最大值 V操作系统= 50μV),MAX9620 (最大TCV操作系统= 0.12μV/°C 和最大值 V操作系统= 10μV)。我们可以说:
Maximum VOS(T) = max VOS(+25°C) + maximum TCVOS × (T-25°C)
现在我们可以以MAX9620运算放大器为例。假设在给定应用中,温度从室温(+25°C)变为+125°C,并且最大V操作系统由于热漂移是:
Maximum VOS(T) = 10µV + 0.12µV/°C × (100°C) = 22µV ….
相比之下,运算放大器的最大失调电压为50μV,最大TCV为5μV/°C操作系统收益 率:
Maximum VOS(T) = 50µV + 5µV/°C × (100°C) = 550µV ….
这些结果表明,在应用中需要高精度的输入失调电压中,热漂移对于输入失调电压非常重要。
由 CMRR 和 PSRR 限制引起的错误
典型运算放大器中的有限共模抑制比(CMRR)会在输入端引入失调电压,从而降低精度。放大器的CMRR越高,对额定输入共模电压的输入失调电压变化越不敏感。在输入信号非常小的应用中,即在mV量级范围内,高CMRR绝对至关重要。
放大器的CMRR是差分增益(A差异) 至共模增益 (A厘米).CMRR也可以用输入失调电压相对于输入共模电压变化(V厘米) 1V。因此:
VOUT = ADIFF × [(VIN+ - VIN-) + ACM × VCM/ADIFF]
等式17也可以称为:
VOUT = ADIFF × (VIN+ - VIN-) + ACM × VCM ……………….
也:
CMRR = ADIFF/ ACM = delta (VCM)/delta(VOS)
有限电源抑制比(PSRR)在引入相对于电源电压变化的额外输入失调电压方面也起着重要作用。电源电压的变化(V抄送)改变内部晶体管的工作点,进而影响输入失调电压。PSRR越高,当电源电压变化时,放大器对输入失调电压的变化就越不敏感。
PSRR = delta (VCC)/delta (VOS)
除非另有说明,否则放大器数据手册的电气特性(EC)表中提供的CMRR和PSRR规格分别在特定输入共模电压和电源电压范围内指定。提供的CMRR规范在整个电源范围内并不相同,提供的PSRR规范在整个输入共模范围内也不相同。3
输入阻抗限制引起的误差
有限输入阻抗(R在) 的运算放大器将与源阻抗 (RS) 驱动放大器并引入增益误差。因此,输入阻抗非常高,大约为109需要欧姆以确保误差可以忽略不计。
在上述情况下输入信号量(V在放大器从源看到的取决于定义为以下的输入阻抗参数:
VIN = VSOURCE × [RIN/(RIN+RS)]………………………..S)].............................
从公式 18 如果 R在>>>·S,然后 V在= VS.
总结
总之,如果不解决输入失调电压、输入偏置电流和有限输入阻抗等直流误差,运算放大器测量将根本不准确。在精度至关重要的高精度应用中,这种性能是不可接受的。设计人员还必须了解数据手册EC表中定义的运算放大器性能规格的重要性和局限性。按照此处介绍的指南,设计人员可以选择正确的运算放大器和具有正确配置的无源元件。最终,在设计中使用最好的运算放大器将消除运算放大器误差并确保尽可能高的精度。
审核编辑:郭婷
-
电源
+关注
关注
185文章
17882浏览量
252295 -
集成电路
+关注
关注
5397文章
11654浏览量
363915 -
运算放大器
+关注
关注
215文章
4977浏览量
173764
发布评论请先 登录
相关推荐
LMP7731单组装与LMP7732双组装高精度运算放大器
运算放大器的测量方式简单介绍
如何通过运算放大器实现ppm精度?
复合放大器:具有高输出功率和高带宽的高精度放大器
如何在运算放大器串联时实现高精度和高输出的功率?
复合放大器:具有高输出功率和高带宽的高精度放大器
运算放大器应用基础
集成运算放大器及其基本应用




 运算放大器的直流误差特性及其对高精度应用的影响
运算放大器的直流误差特性及其对高精度应用的影响











评论