局域实在论与贝尔不等式介绍

1. 局域实在论与贝尔不等式

爱因斯坦以及两位年轻同事波多尔斯基（Boris Podolsky）和罗森（Nathan Rosen）发现量子纠缠与局域实在论的冲突，认为量子力学不完备[1,2]。意思是，除了量子力学中的量子态之外，物理系统还存在额外的变量，可以刻画系统的准确状态。这些额外的变量叫作隐变量，它们代表了所谓的实在论。如果一个代替量子力学的理论包含隐变量，它就叫作隐变量理论。如果这个理论还满足局域性，就叫局域隐变量理论，或者局域实在论。

在EPR论文之前，1931年，冯诺伊曼（von Neumann）就在数学上证明过隐变量不存在[3]。在EPR论文之后，1950到1960年代有一些关于隐变量理论的讨论，特别是玻姆（David Bohm）的一系列工作。1964年贝尔（John Bell）指出（1966年发表），冯诺伊曼的证明并不成立[4]。

1964年，贝尔又提出，局域实在论与量子力学是矛盾的，他发表了一个不等式，是任何局域隐变量理论都应该满足的不等式[5]。后来所有这一类的不等式都叫贝尔不等式，是关于两个子系统的测量结果的关联，每个子系统由一个局域的观察者对之进行测量。用局域隐变量理论计算各种测量结果的关联，其结果满足贝尔不等式，而在量子力学中，如果这两个子系统用某些量子纠缠态描述，那么根据量子力学计算的结果是违反贝尔不等式的。 在这篇题为“论爱因斯坦-波多尔斯基-罗森佯谬”的论文中，贝尔用了玻姆首创的形式，基于自旋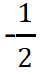语言，但是也适合其他类似的分立变量，如光子偏振。两个粒子的观测量A和B，是自旋值除以恰当的系数，取值都是1或者-1，依赖于隐变量与各自测量方向a和b，因此A(a,λ)=±1, B(b,λ)=±1。根据局域实在论，它们的关联是 P(a,b)=∫dλρ(λ)A(a,λ)B(b,λ)。对于A和B严格关联A(a,λ)=-B(a,λ)，贝尔证明了 1+P(b,c)≥|P(a,b)–P(a,c)|. 而对于自旋纠缠态

，

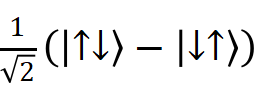量子力学给出P(a,b)= –a•b，选择适当的a、b、c，得到对不等式的违反。对于光子偏振的量子纠缠态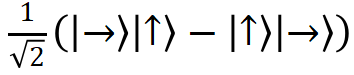




，P(a,b)=-cos2θ，其中θ是a和b的夹角。 量子力学基本问题曾被视为“只是哲学”，贝尔不等式表明，这是有理论、有实验的物理，将原来带有形而上学味道的讨论转变为可以用实验定量决定的判定，将哲学问题转化为定量的科学问题。 检验大自然是否满足贝尔不等式的实验叫作贝尔测试。

作贝尔测试需要使用分居两地又处于量子纠缠态的子系统，也需要迅速高效的探测，以及事先不可预测的对于每个测量装置的独立安排。所有有关贝尔不等式违反（或称贝尔定理）的工作都是在贝尔的开创性工作基础之上发展而来的。

实验判定量子力学胜利，局域实在论失败。但是长期以来，实验判定上存在逻辑漏洞或额外假设，直到近年来才基本消除。而贝尔不等式的提出和验证又与量子信息学的兴起密切相关，包括概念和实验技术。2022年的诺贝尔物理学奖工作就是对这两方面的重大贡献。

2. Bell-CHSH不等式与实验

2.1 CHSH不等式

贝尔最初的不等式的具体形式所依赖的假设过于理想化，比如严格关联，无法在实际实验中核实，因此不适合真实的实验。1969年，克劳泽（John Clauser）、霍恩（Michael Horne）, 西蒙尼（Abner Shimony）和霍尔特（Richard Holt）推广了贝尔的不等式，他们推广后的不等式通常称为CHSH或者Bell-CHSH不等式[6]。

Bell-CHSH不等式更适合实际情况，可以在现实的实验中检验。

延续上面我们对贝尔不等式的讨论。考虑A(a,λ)[B(b,λ)+B(b’,λ)]+A(a’,λ)[B(b,λ)-B(b’,λ)]。它肯定等于±2，因为B(b,λ)+B(b’,λ)与B(b,λ)-B(b’,λ)中必然有一个等于±2，一个等于0。由此得到S=P(a,b)+P(a,b’)+P(a’,b)-P(a’,b’) 满足

–2≤S≤2. 这就是Bell-CHSH不等式。而对于贝尔态，比如，可以达到S=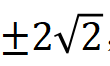，违反Bell-CHSH不等式。   

因此只要有局域实在性，Bell-CHSH不等式即可成立，而且可以在实验上检验。而量子力学违反它。所以，量子力学与局域实在论哪个正确，就看哪个与实验符合。

另外，1989年，塞林格（Anton Zeilinger）曾经与格林伯格（Daniel Greenberg）和霍恩（Michael Horne）发现一种三粒子量子纠缠态具有特别的性质，不需要统计平均，也不需要构造不等式，就与局域实在论存在冲突[7]。

2.2 Freedman-Clauser实验

1969年提出Bell-CHSH不等式时，克劳泽是分子天体物理专业博士生。1970年获博士学位后，他来到伯克利加州大学，成为汤斯（Charles Townes）的博士后，被允许自主研究贝尔不等式。在伯克利，1967年，康明斯（Eugene Commins）的学生科克（Carl Kocher）的博士论文工作是研究来自同一个原子源的光子对的时间关联[8]。

在这个系统中，级联跃迁产生纠缠光子对。钙原子的一个外层电子从基态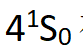被激发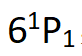到，又跃迁到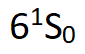，从这个能级跃迁到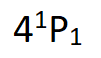，发出一个光子；再跃迁回基态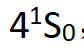，又发出一个光子。为了保持宇称守恒为偶宇称，角动量守恒为0，因此双光子偏振态必然是

。

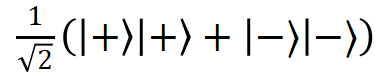在此纠缠态下，光子在两边都被探测到的符合率是，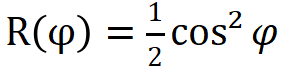

其中φ是检测两个光子的偏振片的夹角。但是科克所选择研究的两个检测光子的偏振片夹角是0度和90度，不能用来检验贝尔不等式。

克劳泽和康明斯的博士生弗里德曼（Stuart Freedman，现已去世）改造了这个实验装置，改进了偏振器的效率。这个系统中，CHSH不等式给出

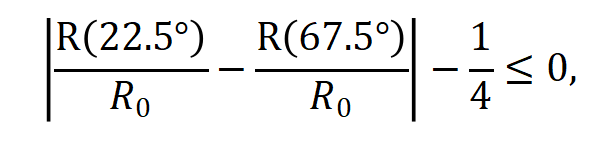
其中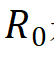是没有偏振器时的符合率。   克劳泽和弗里德曼实验上得到上式左边是0.05±0.008，以6个标准差的实验精度违反贝尔不等式[9]。

克劳泽和弗里德曼实验的漫画示意图（图片来自nobelprize.org） 这个初步的实验尝试有漏洞和局限——产生和探测粒子的效率低，测量也是事先设置好，因此逻辑上，有可能隐变量使得对粒子的探测有选择性，或者测量装置的设置（特别是偏振器的测量方向）影响了光子发出时的偏振，从而导致贝尔不等式的违反，而且不满足局域性要求。

局域性是贝尔不等式的一个关键前提假设。相互分离的两个子系统的测量必须相互独立，包括选择做哪种测量，比如位置还是动量，或者是横向的磁矩还是纵向的磁矩（磁矩正比于自旋），或者偏振片的透光方向。因此必须保证二者的测量时间差足够小，以至于不可能有物理信号从一方传到另一方。因为所有的信号速度不超过光速，实验上必须保证双方测量的时间差小于距离除以光速，用相对论的语言，这叫做类空间隔。弗里德曼-克劳泽实验的固定设置不满足局域性要求。

2.3 阿斯佩实验

1981至1982年，阿斯佩（Alain Aspect）与合作者格朗吉耶（Phillipe Grangier），罗歇（Gerard Roger）和达利巴尔（Jean Dalibard）做了3个实验，以高精度观察到了对Bell-CHSH不等式的违反，在很大程度上满足局域性要求。

在第一个实验中[10]，在发生级联过程前，通过两套激光，用双光子吸收直接将电子激发到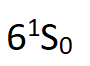，这比以前通过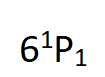有效得多。

在第二个实验中[11]，用双通道偏振器进行测量，得到很好的统计和很大的对贝尔不等式的违反，精度是几十个标准偏差。

贝尔当初就指出，实验设置要在粒子飞行过程中改变[5]。如果两边偏振测量方向做随机的改变，而且所费的时间小于两个粒子从源分别到达偏振器的时间，就能保证纠缠粒子被测量时，时空间隔是类空的，两边的测量没有因果关联。

这在阿斯佩的第三个实验中部分得到实现。这是三个实验中最重要的[12]。从钙原子到偏振片距离6米，光子飞行只有20纳秒，在光子飞行过程中是来不及旋转偏振器的。但是他们用了阿斯佩早些年设计的巧妙方法[13]。一对光子在到达一对偏振片之前，经过一个声光开关，被导向两对偏振器中的一对。声光开关每10ns切换一次。所使用的CHSH不等式给出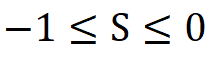，量子力学给出0.112。

实验得到0.101±0.020, 与量子力学一致，违反不等式。精度是5个标准偏差。

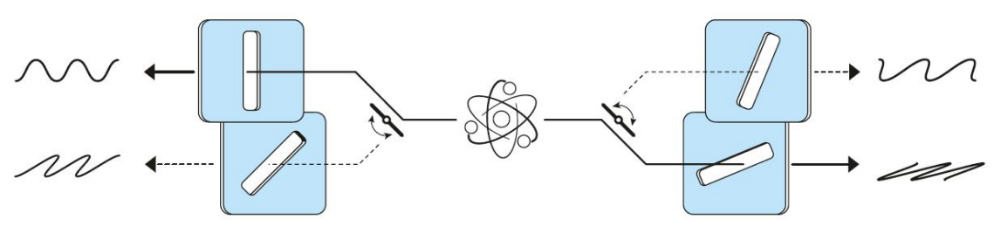
阿斯佩的第三个实验的漫画示意图（图片来自nobelprize.org） 这些实验以及后来的很多贝尔测试实验都判定量子力学胜利，局域实在论失败。但是这些工作中仍然存在技术性的逻辑漏洞，如在探测器效率或局域性上。

在阿斯佩的第三个实验中，因为在纠缠光子对离开源之后，偏振器的测量方向做了改变，所以逻辑上来说，在很大可能性上，光子产生时的偏振没有受到偏振器测量方向的影响。

但是，这两个偏振器之间距离很短，由于技术的局限性，做不到在光子飞行时，随机改变测量装置。因此在阿斯佩的第三个实验中，测量装置的改变并不是随机的，而是周期性的。具体来说，我觉得逻辑上，不能排除比较复杂的“阴谋论”：既然测量装置的改变是周期的，那么测量时的偏振器方向与过去的偏振器方向的关系是确定，所以后者也可能影响了光子产生时的偏振。因此阿斯佩的第三个实验并没有关闭局域性漏洞，但是仍然具有里程碑的历史地位。

2.4 塞林格组补上局域性漏洞

1997年，塞林格研究组的实验终于补上了局域性漏洞[14]。在他们的实验中，分析纠缠光子对的实验装置相距400米，以光速飞行则需要1300纳秒。纠缠光子对通过光纤传到偏振片。每个光子的偏振分析装置的方向有足够的时间进行快速的随机改变——用随机数产生器控制，用原子钟计时。一系列光子对的测量结束后，实验人员将两边的数据搜集起来，分析关联。

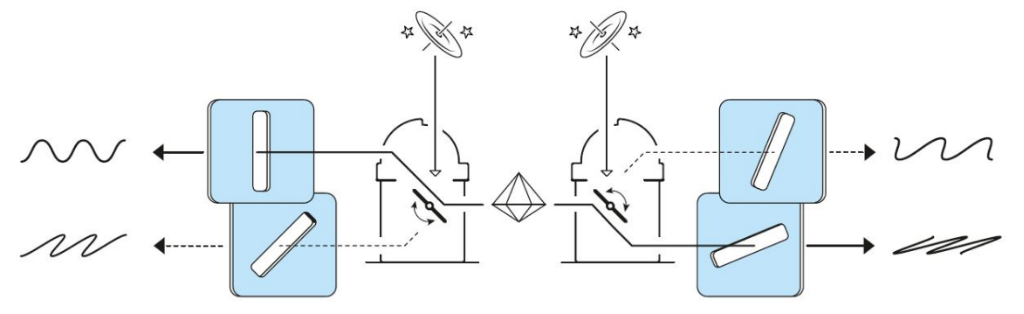
塞林格研究组的贝尔测试实验的漫画示意图（图片来自nobelprize.org）。 在补上局域性漏洞后，塞林格组又做过很多贝尔测试，其中一个实验用来自不同类星体的光子的波长信息来决定偏振测量方向[15]，这反映在漫画中。与此同时，潘建伟组的实验用来自不同恒星的光子的波长信息来决定偏振测量方向[16]。

在这个实验中，各种技术改进很多。值得指出，这里用第2类参量下转换（type-II parametric down conversion）方法产生纠缠光子对。这是一个非线性光学过程，用β-BBO（偏硼酸钡）晶体实现。β-BBO晶体是由中国科学院福建物质结构研究所首次发现和研制的紫外倍频晶体。这种方法产生的纠缠光子对，可以通过光纤传送，从而分开很大的距离。这个方法最早由欧泽宇和L. Mandel, 以及史砚华和C. O. Alley于1980年代实现，并以此做了贝尔测试[17,18]，后来欧泽宇， Pereira, Kimble和彭堃墀用这个方法实现了连续变量（所谓的光振幅）的纠缠以及贝尔测试[19]。后来人们用这个方法实现了相距几公里[20]和几十公里[21]的纠缠光子的贝尔测试。塞林格组对此方法的使用始于与史砚华的一个合作工作，在4分钟内实现了100标准偏差以上的贝尔不等式违反[22]。

我们前面说过，爱因斯坦等人揭示了量子纠缠与定域实在论（即定域性和实在论共同成立）的冲突，爱因斯坦是量子纠缠研究的最大功臣。但是正如阿斯佩曾经说过的，在相对论性分离（即类空间隔）下所选择的测量下，对贝尔不等式的违反，意味着“用粒子共同源决定的、由光子对携带的共同性质来解释关联”这样的爱因斯坦图像不能保持了，我们必须做出结论：纠缠粒子对确实是不可分离的整体，无法赋予其中每个粒子单独的局域性质[23]。

3.后续工作

在关于贝尔不等式的实验中，还长期存在“探测漏洞”。因为被探测到的纠缠粒子只是最初产生的纠缠对中的一部分，有多少被探测到与实验装置有关。

在公平取样的前提下，实验上得到的统计分析才可以用来检验贝尔不等式。但是探测器的效率是有限的，如果探测效率不够高，就可能做不到公平取样，这就是探测漏洞。

要补上探测漏洞，保证公平取样，必须满足这样的条件：当一边测量到光子时，另一边也探测到光子的概率大于2/3[24]。2001年和2008年的离子实验[25,26]补上了探测漏洞。2013年，塞林格组[27]和Kwiat组[28]在光子实验中也补上探测漏洞。

2015年，有几个实验都同时补上局域性漏洞和探测漏洞，塞林格组[29]和NIST的Shalm组[30]都用了可以快速改变的偏振片和高效率的光子探测器，Delft的Hensen组用两对电子-光子对[31]，测量两个光子，使得两个电子纠缠。后来，在2017年Weinfurter用相距398米的纠缠原子也同时补上这两个漏洞[32]。

下面再介绍一下“自由选择漏洞”。贝尔不等式是关于两个子系统的各种测量结果之间的关联，涉及测量装置的几种不同设置，比如测量的方向。这在贝尔不等式的推导中是完全自由的，与隐变量无关。

而在贝尔测试中，需要自由随机选择这几个不同设置。长期以来，在实验中，即使局域性漏洞和探测漏洞都补上了，也还是由仪器来随机选择实验装置的安排。这并不理想，因为万一这些仪器所作的选择本身就是由隐变量决定的呢？这叫做“自由选择漏洞”。贝尔曾提出可以用人的自由选择来保证实验装置的安排的不可预测性。但是当时的技术做不到。

2016年11月30日，一个叫做“大贝尔测试”（The Big Bell Test）的实验项目就是这样的实验，补上了这个“自由选择漏洞”。实验中所作的选择都是来自全球各地的约10万个志愿者。12小时内，这些志愿者通过一个网络游戏“The BIG Bell Quest”，每秒产生1000比特数据，总共产生了97347490比特数据。参加游戏的志愿者被要求在一定时间内输入一定的随机比特0或1，被用于对实验中所作选择的指令。有个机器学习算法会根据已输入的比特，提醒志愿者避免可预测性，但是对产生的数据不作选择。

全球五个洲的12个实验室在12个小时内做了13个贝尔实验。这些实验用10万名志愿者无规提供的这些数据来安排测量装置，不同的实验采用不同的数据。在不同系统的贝尔测试的结果表明了局域实在论在这些系统中被违反。其中几个是潘建伟组、塞林格组等分别完成的光子偏振实验。

2018年5月9日，Nature杂志以“用人的选择挑战局域实在论”为题， 发表了这13个贝尔实验的结果[33,34]，显示局域实在论在光子、单原子、原子系综与超导器件等系统中被违反。这一工作代表了对量子力学基本理论的检验又前进了一步。

最后提一下，既然局域实在论与量子力学冲突，那么矛盾的源泉来自哪里，局域论还是实在论？为研究这个问题，莱格特（Anthony J. Leggett）考虑一种“加密非局域实在论”：作为非局域性，对于确定的偏振方向，被测量量既依赖测量偏振片方向，也依赖于另一边的偏振片方向。但是物理态是各种偏振方向的统计平均，服从局域规律，如马吕斯定律。对此，莱格特导出莱格特不等式，被量子力学违反[35]。最近我们提出一个推广的莱格特不等式，特别适用于粒子物理中的纠缠介子，被量子力学和粒子物理违反[36]。

2022年诺贝尔物理学奖授予克劳泽、阿斯佩和赛林格，奖励他们关于纠缠光子的实验，奠定了贝尔不等式的违反，也开创了量子信息科学。他们的开创性实验使量子纠缠成为“有力的工具”，为量子科技的新纪元打下基础。

审核编辑：刘清