了解集成解决方案如何提高电阻电流检测的精度

在本文中，我们将讨论为什么分立式实现无法提供高精度的电阻电流检测。

分立放大器和一些外部增益设置电阻可用于提高电流检测电阻两端的电压。 虽然这种分立式解决方案具有成本效益，但由于外部元件的匹配有限，它们无法提供高精度。 尝试使用高精度电阻网络可以抵消使用简单分立解决方案可能节省的成本。

电阻电流检测的分立式实现

在一个
上一篇文章，我们讨论了基于运算放大器的同相配置可用于检测和增益低侧电流检测电阻两端的电压。 同相配置具有单端输入，并检测其相对于地的输入电压。 这就是为什么我们不能在高端检测配置中使用该放大器的原因。

另一方面，经典差动放大器具有差分输入。 由于它检测分流电阻器两端的压降，而不是节点相对于地的电压，因此可用于低侧和高侧电流检测应用，如 图1.

在本文中，我们将讨论使用差动放大器时可能影响精度的两个重要误差源。

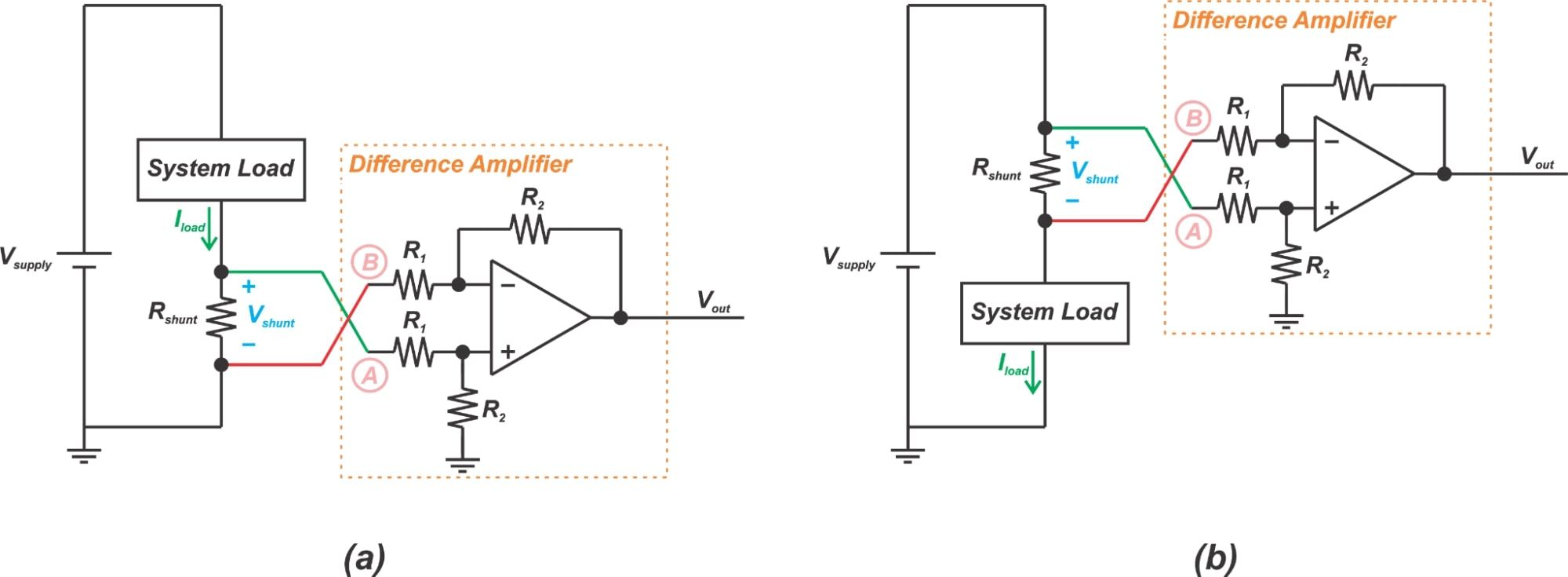
图1. 在（a）低端和（b）高边电流检测中使用差动放大器。

共模抑制比：关键特性

共模抑制比是差分输入放大器抑制两个输入共有的信号的能力。 放大器的传递函数可以表示为：

[v_{out}=A_{dm}v_{d}+A_{cm}v_{c}]

等式 1.

其中\\（A_{dm}\\）和\\（v_{d}\\）分别是放大器的差模增益和放大器输入端的差分信号。 类似地，\\（A_{cm}\\） 和 \\（v_{c}\\）
是施加到放大器的共模增益和共模信号。 根据 等式 1，放大器输出端出现的电压是输入共模值的函数。 在
图1（b），理想情况下，我们期望输出是差分信号V的函数分流。 然而，实际上，输出也是电源电压V的函数。 供应。

当我们改变 V 时供应，放大器输入端的共模信号，因此放大器的输出电压发生变化。 即使我们保留 V 也会发生这种情况分流
不断。 为了减少这种非理想效应，我们需要使共模增益厘米
远小于差模增益A分米。 共模抑制比（CMRR）定义为差分增益除以共模增益，它规定了放大器在放大差分信号时抑制共模信号的能力。

分立式实现具有低 CMRR

考虑 中所示的差动放大器 图2.

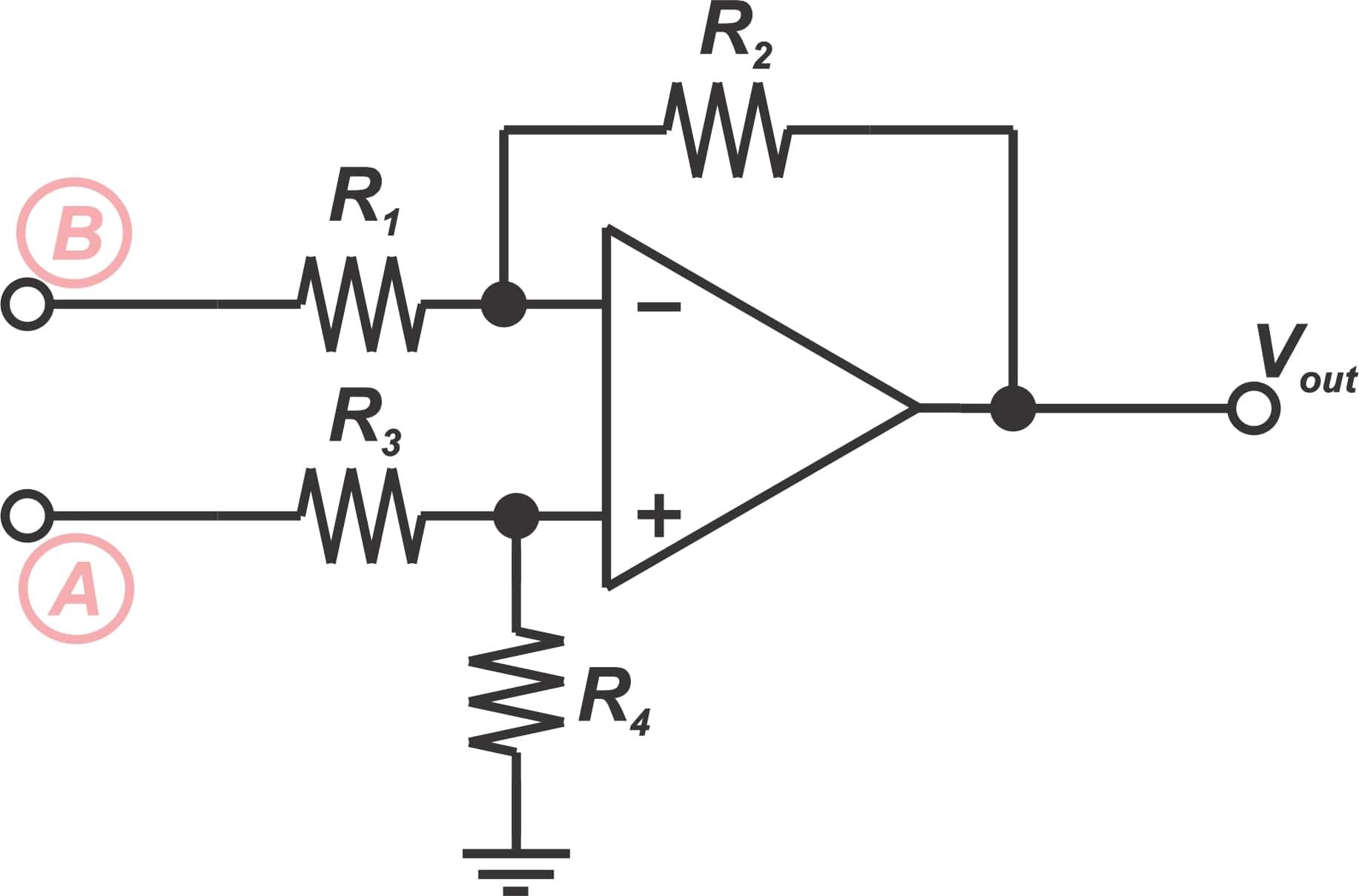
图2.

对于理想的运算放大器，差动放大器的传递函数由下式给出：

[v_{out}=\\frac{R_{4}}{R_{1}}\\times\\frac{R_{1}+R_{2}}{R_{3}+R_{4}}\\timesv_{A}-\\frac{R_{2}}{R_{1}}\\times v_{B}]

对于\\（\\frac{R_{2}}{R_{1}}=\\frac{R_{4}}{R_{3}}\\），我们有：

[v_{out}=\\frac{R_{2}}{R_{1}}\\left（v_{A}-v_{B}\\right）]

等式 2.

这个公式表明，任何共模电压都将被放大器完全抑制，即\\（v_{A}=v_{B}\\），我们有\\（v_{out}=0\\）。 然而，在实践中，差动放大器的共模抑制将受到限制，因为比值\\（\\frac{R_{2}}{R_{1}}\\）不完全等于\\（\\frac{R_{4}}{R_{3}}\\）。
可以显示 差动放大器的CMRR由下式给出：

[CMRR\\simeq \\frac{A_{d}+1}{4_{t}}]

等式 3.

Ad是差动放大器的差分增益，等于 R2/R1; t是电阻容差。 例如，当差分增益为1%和0.1%电阻时，我们有：

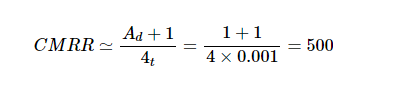
以dB表示该值，我们得到的CMRR约为54 dB。 请注意， 等式3基于运算放大器是理想且具有非常高的CMRR的假设得出的。 如果运算放大器的CMRR不比公式3获得的值大多少，则需要使用 更复杂的方程。

集成解决方案可导致高 CMRR

因此，即使使用理想的运算放大器，差动放大器的CMRR也相对较低，并受到增益设置电阻匹配的限制。 为了解决这个问题，我们可以使用一系列匹配的电阻网络，例如LT5400.LT®5400 是一款四通道电阻器网络，具有 0.005% 的出色匹配，可用于创建具有高 CMRR 的差动放大器，如
图3.使用匹配的电阻网络，应该可以实现约80 dB的CMRR。

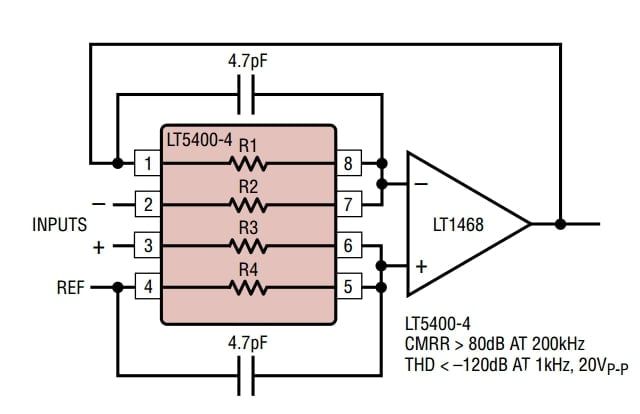
图3. 电阻阵列可用于创建具有非常高CMRR的差动放大器。 图片由 凌力尔特

分立放大器和一些外部增益设置电阻可被视为低成本电流测量解决方案。 但是，如您所见，增益设置电阻的匹配决定了放大器的CMRR。 尝试使用单独的高精度电阻网络可以抵消使用简单差动放大器可能节省的成本。

我们可以使用完全单片的解决方案，例如 AMP03ADI公司将激光调整电阻集成到精密运算放大器封装中，以实现电阻之间的高度匹配。 这种集成解决方案可以获得大于100 dB的CMRR。

另一个误差源：增益设置电阻的温度漂移

增益设置电阻的温度漂移是影响测量精度的另一个因素。 如上所述，增益设置电阻的容差决定了放大器在室温下的初始精度。 但是，为了使电阻比恒定，电阻在工作温度范围内应表现出类似的行为。

为了更好地理解温度漂移如何产生增益误差，让我们考虑一个例子。 假设电阻值在 等式2 R1=5 kΩ 和 R2=100kΩ。 此外，假设电阻的温度系数为±50 ppm/°C，环境温度可能比参考温度（室温）高100°C。

差分增益的最大值和最小值是多少 R2R1R2R1？

高于基准温度100 °C的温升可使±50 ppm/°C电阻的值改变±0.5%。 因此，最大差分增益由下式给出：

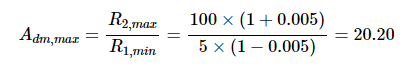
最小增益由以下公式获得：

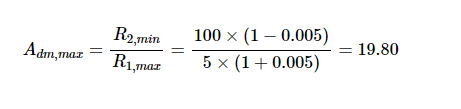
请注意，电阻器可能会沿相反方向漂移。 在本例中，1%的增益误差仅由漂移效应引起，因为我们假设电阻在室温下具有其标称值。

有趣的是，对于匹配的电阻网络，例如 LT5400 或完全单片式电流检测解决方案，集成电阻器可以表现出近乎完美的初始误差和温度漂移匹配。
图5.

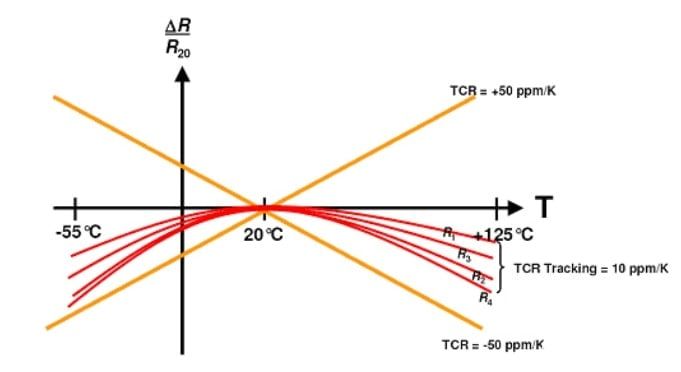
图5. 图片由 维沙伊

在此图中，橙色线表示单个±50ppm/°C电阻的值变化限值，当温度从参考温度（20°C）向任一方向变化时。 红色曲线表示匹配电阻阵列的四个集成电阻的温度行为。

虽然来自匹配电阻网络的单个电阻可以表现出±50ppm/°C的温度系数，但四个集成电阻的温度行为非常匹配。 电阻值随着温度的变化而相互跟踪。 这些匹配电阻使我们能够在工作温度范围内保持放大器增益相对恒定。

结论

分立放大器和一些外部增益设置电阻可用于提高电流检测电阻两端的电压。 虽然这种分立式解决方案具有成本效益，但由于外部元件的匹配有限，它们无法提供高精度。

增益设置电阻的匹配决定了放大器的CMRR。 为了实现高CMRR，电阻的初始误差和温度漂移需要近乎完美的匹配。 这就是为什么集成解决方案可以轻松击败CMRR方面的离散实现。 请注意，尝试使用单独的高精度电阻网络可以抵消使用简单分立解决方案可能节省的成本。