射频设计基础—传输线简介

了解电压波及其与射频 （RF） 电路设计的重要基本概念（传输线）的关系。

电路设计中的一个重要因素是电路元件和互连相对于正在处理的信号波长的物理尺寸。 当信号频率足够低，以至于互连的物理尺寸小于信号波长的十分之一左右时，我们可以假设沿导线的不同点具有相同的电位并且具有相同的电位
当前。

从实际的角度来看，这是一个令人满意的假设，可以显着简化低频电路设计。 但是，当我们进入更高的频率时，我们可能需要将信号描述为沿导线传播的波。 在这种情况下，信号幅度是时间和位置的函数。

电压波沿导线传播的信号

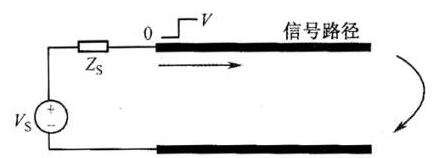
例如，考虑应用正弦输入 Vs源阻抗为 R 的 cos（⍵t）s 到负载阻抗 RL 通过一对长线（图1（a））。

图1. 使用一对长导线 （a）、时间正弦函数波形 （b） 和显示沿导线电压的波形 （c） 的示例。

假设 x 轴方向的导线的长度远大于信号波长。 此外，假设互连具有统一的结构和不同的参数，例如导体尺寸、导体之间的间距等，沿导线相同。

沿导线出现的稳态电压和电流信号取决于许多参数的值; 但是，为了描绘该电路行为的定性图景，我们假设电压波可以用公式1来描述：

v（x，t）=Acos（ωt−βx）v（x，t）=Acos（ωt−βx）等式 1.

其中A和β是一些取决于电路参数的常数。 如图所示，电压信号是时间（t）和位置（x）的函数。 在固定位置 x =x1，βx项是一个常相位项，上面的波形只是时间的正弦函数（图1（b））。 此正弦函数的周期 T 为：

ωΔt=2π→T=Δt=2poΔt=2π→T=Δt=2po

为了检查波形与位置的依赖性，我们可以查看特定时刻的波形 t = t1.在这种情况下，项 ⍵t 变为常相项，我们观察到电压信号是位置 x

的正弦函数。图1（c）中的示例波形显示了在给定时间点沿导线的电压如何沿互连正弦变化。该波形可以被认为是x在导线长度上的周期函数。期间由以下人员给出：

βΔx=2π⇒Δx=2πββΔx=2π⇒Δx=2πβ

上式指定了给定时刻沿导线的两个连续相等信号值之间的距离。这实际上是通常由公式2表示的波长的定义：

λ=2πβλ=2πβ等式 2.

传播方向和速度

就像水波在特定方向上传播一样，电波也会在特定方向上传播。例如，考虑公式1中的波函数。在给定时间（t2），位置 （x ） 处的函数值2） 是：

v（x2，t2）=Acos（ωt2−βx2）v（x2，t2）=Acos（ωt2−βx2）

考虑到这一点，假设此值对应于图 2（a） 中的点 A。

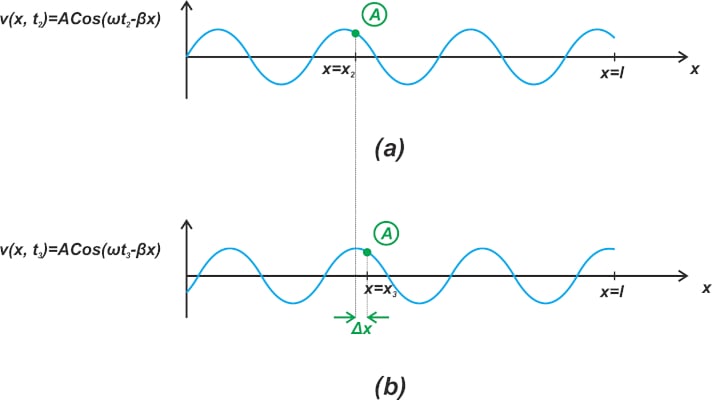
图2. 示例波形，其中 （a） 显示位置 （x2） 为 A，（b） 显示位置 （x3） 是向右移动的 A。

随着时间的流逝，点 A 将朝哪个方向移动？如果点 A 的下一个位置是 x3 在时间，T3，（图2（b）），我们应该有：

v（x3，t3）=v（x2，t2）⇒cos（ωt3−βx3）=cos（ωt2−βx2）v（x3，t3）=v（x2，t2）⇒cos（ωt3−βx3）=cos（ωt2−βx2）

简化为公式3：

ωt2−βx2=ωt3−βx3→x3−x2t3−t2=ωβωt2−βx2=ωt3−βx3→x3−x2t3−t2=ωβ等式 3.

假设β是正值，并注意到3 》 吨2， x3 应大于 x2.换句话说，点 A 沿正 x 方向行进。但是，您可能想知道，公式4中的以下波函数呢？

v（x，t）=Acos（ωt+βx）v（x，t）=Acos（ωt+βx）等式 4.

该波上给定点的下一个位置对应于保持 ⍵t + βx 恒定的 x 值。由于术语 ⍵t 随时间增加，因此 x

应该减小。因此，该波沿负x方向传播。公式3实际上给出了传播速度（也称为相速度（vp） 的波）：

vp=ωβvp=ωβ

射频波反射

幸运的是，各种类型的波，包括机械波、电波、声波和光波，其行为基本相似。这有助于我们利用来自更具体类型（例如水波）的直觉来更好地理解其他类型的行为。各种波的一个相似之处是，当它们所经历的介质的某些特性发生变化时，它们会反射。

例如，当向岸边行进的水波与岩石碰撞时，它会反射并传播回海洋。同样地 当波介质的阻抗发生变化时，电压波会反射。

在图1（a）所示的示例中，当负载阻抗R时，沿正x方向传播的波反射L 与互连的特殊属性不匹配，称为特性阻抗（通常用Z表示0）。反射后，产生负x方向的波，从负载向电压源传播。因此，一般来说，我们可以预期入射波和反射波沿着导线同时传播。反射电压与入射电压之比定义为 反射系数 并用ΓΓ 表示。

阻抗匹配：射频工程师的痴迷

由于某些入射功率会反射回电源，因此负载无法接收到电源提供的最大功率。因此，反射系数是一个重要参数，它决定了实际到达负载的可用功率。为了实现最大的功率传输，负载阻抗应与线路的特性阻抗相匹配。

负载不匹配的另一个问题是入射波和反射波的叠加会沿导线产生较大的峰值电压，从而损坏我们的电路组件或互连。上面的讨论表明，在处理高频信号时，我们需要具有精确控制参数的互连，以预测波沿互连传播时的行为。例如，应精确控制导体的尺寸、它们之间的距离以及分隔导体的电介质类型。这些专用互连称为输电线路 将它们与普通互连区分开来。

射频波尺寸

根据经验，如果电线的物理长度约为λ15λ15，则应将电信号视为穿过导线的波。

图 3 可帮助您直观地了解将导线长度限制为 λ15λ15 如何减少随位置变化的信号。

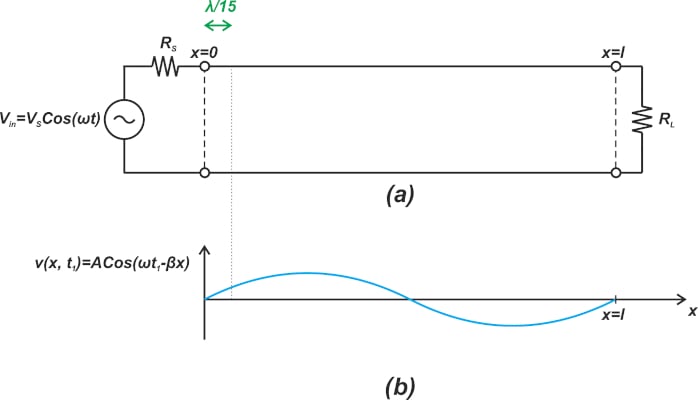
图3. 一个示例，显示通过限制导线尺寸 （a） 使信号如何随位置 （b） 而变化。

一些参考文献建议物理大小为 λ10λ10 作为信号随位置变化的阈值，预计在该阈值上，信号随位置的变化会很大。

现在我们对电波和传输线有了定性的理解，让我们来看看传输线的等效电路，看看如何消除反射。

传输线等效电路

当导线尺寸与波长相当时，我们正在处理沿导线传播的电波。 在这种情况下， 基尔霍夫电路定律 （电压定律 和 电流定律）不能直接应用。 但是，我们仍然可以找到高频双导体互连的等效电路。 为此，将线划分为长度无穷小的单元，并且每个元素被建模为一个网络 感应器一个 电容器和两个电阻。 如图 4 所示。

图4. 显示传输线元件的示例：电感器、电容器和两个电阻器。

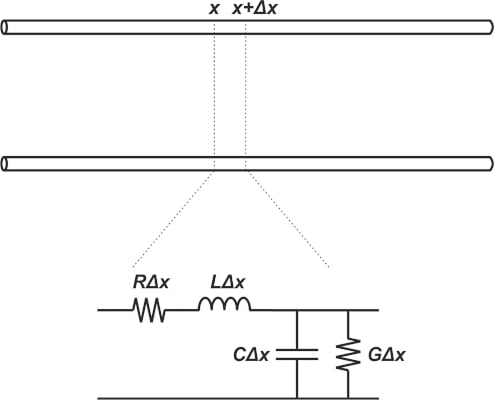
在这里，R 和 G 分别表示 电阻 每单位长度的导线和分离导体的电介质的每单位长度的电导。 L和C表示传输线每单位长度的电感和电容。

在射频下，串联电抗通常远大于串联电阻，而并联电抗通常远小于并联电阻，因此我们可以假设这两个电阻都可以忽略不计。 忽略R和G分量，可以通过图5所示的无限梯形网络对无损传输线进行建模。

图5. 无限梯形图网络的模型。

通过阻抗匹配消除反射

有了无限长的传输线，入射波将永远向前传播，并且不会有反射！ 让我们看看我们是否可以通过适当选择实际有限长度传输线的参数来模拟这种理论情况。 对于无限长的传输线，等效电路中有无限数量的段，如图5所示。

如果我们向这个无限梯形网络添加另一个无穷小部分，输入阻抗应该保持不变。 换句话说，如果图6中的图表对应于一条无限长的传输线，则从节点A和B“看到”的输入阻抗是相同的。

图6. 无限长的传输线示例。

因此，我们可以简化上图，如图 7 所示。

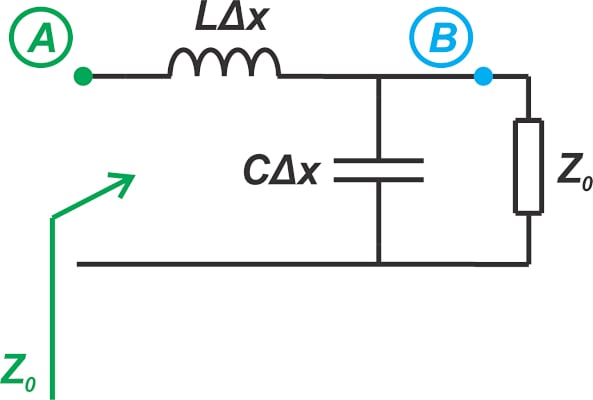
图7. 图6的无限长传输线示例的简化。

在此图中，输入阻抗为：

Z_0 = L \\Delta x s+\\big（ \\frac{1}{C \\Delta x s} \\parallel Z_0 \\big）Z_0 = L
\\Delta x s+\\big（ \\frac{1}{C \\Delta x s} \\parallel Z_0 \\big）

使用一点代数，我们得到：

CZ20−L−LCΔxZ0s=0CZ02−L−LCΔxZ0s=0

由于 Δx →→ = 0，我们可以忽略第三项，导致：

Z0=√LCZ0=LC

上式给出了理想、无损、无限传输线的输入阻抗。 由于这是传输线的重要特性，因此赋予了它一个特殊名称：传输线的特性阻抗。 我们如何利用这些信息来消除有限长度传输线中的反射？ 如上所述，从源的角度来看，图6和图7中的电路是等效的。 这表明，如果将传输线端接到等于线路特性阻抗的负载电阻，则从源的角度来看，传输线将显示为无限长的线，并且不会发生反射。

耗散能量的无功组件网络！

有趣的是，虽然整个网络由电抗元件组成，但输入阻抗是一个正的实值。 纯电抗元件无法耗散功率; 然而，上面的分析表明，整个网络可以通过一个电阻器建模，因此，它正在耗散能量！

答案在于假设网络是无限长的。 这样的结构是一个有趣的抽象，但在物理上是不可能的。 在无限传输线中，能量永远沿着输电线路向动。 它不会被任何电感器或电容器消耗。 这条线就像一个能量黑洞。

当我们设置 R 时L = Z0，负载电阻器以无限长的传输线能够永久吸收能量的方式永久耗散能量。 因此，反射被省略。