使用数字电位计校准电源

电阻反馈网络通常用于设置电源的输出电压。机械电位器（电位器）方便地解决了调节电源的问题。为了便于自动校准，可以用数字电位器代替机械电位器。本应用笔记介绍了一种使用数字电位器的校准解决方案，因为数字电位器更小，不会随着年龄或振动而移动，并且可以远程重新校准。该解决方案降低了系统对数字电位器端到端电阻容差的敏感性，使该解决方案成为设计人员的最佳选择。本应用笔记还解释了计算电阻链值和以这种方式使用数字电位器所需的一些公式。提供具有标准 reisistor 值的电子表格，以便于计算。

介绍

电阻反馈网络通常用于设置电源的输出电压，因为固定电阻器易于使用且成本低。但是，由于固定网络不可调，因此无法准确设置输出电压。因此，许多电源在反馈网络中使用机械电位器（电位器）来设置输出电压。为了便于自动校准，可以用数字电位计代替机械电位计。数字电位计更小，不会随着年龄或振动而显着移动，甚至可以远程重新校准。本应用笔记解释了以这种方式使用数字电位器所需的一些计算，并提供了一个电子表格，以便于计算。

常规电源反馈

电源通常使用阻性反馈来设置输出电平。然而，由于器件容差很多，都会影响输出电压，因此固定电阻分压器通常是不够的。在这些情况下，使用可变电阻比，以便在最终测试中校准系统。

虽然传统上会使用机械电位计，但在许多应用中，这些元件已被数字电位计所取代。数字电位器不会受到明显的老化影响，并且在最终测试中自动调整要简单得多。

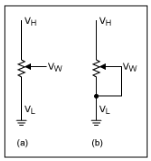
固定电阻和机械电位计方案如图1和图2所示。

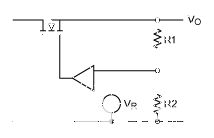
图1.传统的固定电阻反馈。

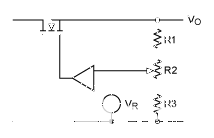
图2.传统的可变电阻反馈。

以具有2.5V基准电压的12V电源的典型示例为例。基准电压和系统中的所有其他器件将具有容差。方便的是，所有公差都可以表示为基准上的附加公差。在本例中，我们将使用 ±5% 的典型总公差作为参考。

计算固定电阻反馈的值基于一个简单的公式：

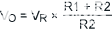（公式1）

由于在此示例中，VR将具有 ±5% 的容差，这导致输出电压的容差为 5%。如果这在应用中不可接受，则需要使电阻分压器可变。通常不会用机械电位计代替R1和R2，因为这会导致输出电压范围很宽，并且对调整非常敏感。随着时间的推移和温度，电位器位置的任何漂移都会产生不可接受的输出电压漂移。因此，图2展示了一种减小输出范围的方案，现在更容易调整，也更稳定。

假设，我们应该能够用数字电位器代替R2，并且我们应该有一个电动可调系统。然而，事情并没有那么简单。首先，需要对数字电位器进行一些解释。

数字电位器的基本结构

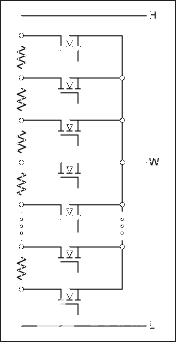
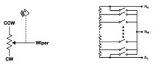
图3.典型的数字电位计结构。

数字电位器通常是一串电阻，每个节点都有一个开关，如图3所示。为简单起见，这些开关显示为单个MOSFET。通常，这些开关将是两个BiCMOS晶体管（一个“P”和一个“N”），以产生低导通电阻。

这种结构通常用于多达 256 个水龙头的锅。当电位器高于 256 个抽头时，使用更复杂的分段结构可能更有效。但是，这超出了本应用说明的范围。

由于所有电阻器都在同一芯片上制造，因此它们将非常紧密地匹配。不幸的是，端到端电阻可能没有那么明确定义。典型的数字电位器是MAX5402，这是一款单通道、256抽头器件，端到端电阻为10kΩ （典型值）。然而，端到端电阻容差为±20%。在比率学上，它的定义要好得多，积分非线性（INL）为0.5 LSB（最大值）。因此，它非常适合用作电位分隔器。

使用数字电位器校准电源

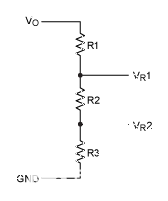
图4.初始电阻串。

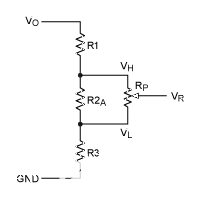
图5.最终电阻串。

电阻值R1、R2和R3的计算方法如图4所示。我们将使用以下示例：

VO= 12V
VR= 2.5V ±5%
RT= R1 + R2 + R3

初始方程很简单，定义如下：

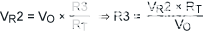（公式2）

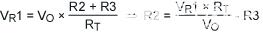（公式3）

R1 = RT- R3 - R2

（公式4）

第一步是定义 R 的总电阻T，使用 （R1 + R2 + R3）。由于这是任意的，我们将从 R 开始T= 20kΩ。（如果需要，我们以后可以随时更改它，以便为 R1、R2 和 R3 提供更真实的值。从公式2中，我们发现R3 = 3.598kΩ。根据公式3，R2 = 417Ω，从公式4，R1 = 15.625kΩ。

显然，计算出的理想电阻值通常不可用，因此需要使用标准电阻值。最接近的1%值替换为R1和R3：R1 = 15.8kΩ，R3 = 3.92kΩ。（为方便起见，我们在电子表格中包含了标准电阻值图表。

现在我们可以向后计算以找到R2的理想值，如公式5所示。R2 最终将变为可变值。因此，计算其值，以便 VO当 R2 倾斜且 V 倾斜时将是正确的R是其标称值。

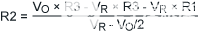（公式5）

因此，R2 = 646Ω。

我们需要考虑到这样一个事实，即数字电位器的端到端容差非常差。将大值数字电位器与小值固定电阻并联是降低电位器端到端容差差影响的简单方法。如图 5 所示。因此，R2的并联组合一个和 RP生成 R2。

使用公式6，最后一步是计算并联固定电阻的值，给定一个电位计标称端到端电阻。

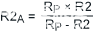（公式6）

因此，使用10kΩ电位器进行RP，R2 的理想值一个为690Ω。最接近的1%值为698Ω。如果我们计算这个和数字电位器在其公差极值下的并联组合，我们得到R最低= 642Ω 和 R.MAX= 660Ω.由于锅的端到端公差为20%，因此公差仅为1%。我们使用698Ω电阻作为R2一个，因为这是最接近的标准 1% 值。

最终计算证实，使用实际值时，数字电位器可以覆盖基准电压源容差所需的5%范围。我们可以使用星三角变换，如图 6 所示。我们显然不需要计算 R6。

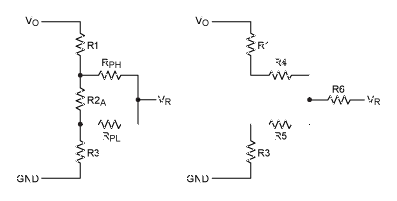
图6.使用星三角变换。

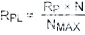（公式7）

其中 N 是抽头位置，NMAX 是最大抽头位置。

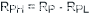（公式8）

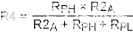（公式9）

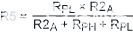（公式10）

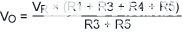（公式11）

使用这些公式，我们确认电位器的范围将涵盖参考的公差范围。

要汇总要求和所选组件值，请执行以下操作：

VO= 12V （输出电压）
VR= 2.5V ±5% （基准电压） R1 = 15.8kΩ （上部电阻）
R1 = 15.8kΩ (upper resistor)
R2一个= 698Ω （并联电阻）
RP= 10kΩ （数字电位计） R3 = 3.92kΩ （下电阻）
R3 = 3.92kΩ (lower resistor)

以下抽头点将所需的输出电压设置在基准容差的极端值。

VR= 2.375V， 抽头 = 44， VO= 11.99842V
VR= 2.625V，抽头 = 210，VO= 11.99773V

可以进一步优化以降低输出电压阶跃。但是，电位计在两端确实有一些开销，以考虑任何进一步的容差。

总结

本应用笔记讨论了调整电源的问题，以及如何使用机械电位器解决这个问题。此外，本文还介绍了使用数字电位器的校准解决方案，因为数字电位器更小，不会随着年龄或振动而移动，并且可以远程重新校准。该解决方案还降低了数字电位计端到端电阻的容差，使该解决方案成为设计人员的最佳选择。开发了计算电阻链值所需的公式，并提供了包含标准电阻值图表的电子表格。

审核编辑：郭婷