步进电机原理与驱动附件中附带电路与程序

步进电机概述：

步进电机驱动器的细分原理介绍，步进电机安装有带永久磁性的转子，而定子至少具有两个绕线。当转子磁性与定子绕线保持一致时，将驱动第二个绕线。两个绕线交替开启和关闭，这将导致电机锁定在想要的步进位置。通过绕线的电流方向还可反向。在带有两个定子绕线的步进电机中，有四个步进以 90 °隔开。步进电机驱动器的细分原理介绍，根据向定子绕线提供的脉冲，可精确控制步进电机移动的步进。步进电机的速度控制可通过向绕线提供脉冲频率实现，而旋转方向可通过反向脉冲序列进行更改。电机内部的极片有许多齿，有助于定位相对于定子的转子位置。一些步进电机的定子级也有齿。根据使用的控制技术，可全步进、半步进或微步进控制步进电机。简单的方形脉冲可以控制处于全步进的电机，而先进控制技术（如脉宽调制 (PWM)）可用于微步进。步进电机驱动器的细分原理介绍，在国内，大家对细分还不是特别了解，有的只是认为，细分是为了提高精度，其实不然，细分主要是改善电机的运行性能，现说明如下：步进伺服电机的细分控制是由驱动器精确控制步进电机的相电流来实现的，以二相电机为例，假如电机的额定相电流为3A，如果使用常规驱动器（如常用的恒流斩波方式）驱动该电机，电机每运行一步，其绕组内的电流将从0突变为3A或从3A突变到0，相电流的巨大变化，必然会引起电机运行的振动和噪音。如果使用细分驱动器，在10细分的状态下驱动该电机，电机每运行一微步，其绕组内的电流变化只有0.3A而不是3A，且电流是以正弦曲线规律变化，这样就大大的改善了电机的振动和噪音，因此，在性能上的优点才是细分的真正优点。由于细分驱动器要精确控制电机的相电流，所以对驱动器要有相当高的技术要求和工艺要求，成本亦会较高。需要注意的是，国内有一些驱动器采用平滑来取代细分，有的亦称为细分，但这不是真正的细分，一定要分清两者的本质不同。

步进电机驱动器的细分1．平滑并不精确控制电机的相电流，只是把电流的变化率变缓一些，所以平滑并不产生微步，而细分的微步是可以用来精确定位的。步进电机驱动器的细分2．电机的相电流被平滑后，会引起电机力矩的下降，而细分控制不但不会引起电机力矩的下降，相反，力矩会有所增加。步进电机驱动器的细分原理介绍，步进电机安装有带永久磁性的转子，而定子至少具有两个绕线。当转子磁性与定子绕线保持一致时，将驱动第二个绕线。两个绕线交替开启和关闭，这将导致电机锁定在想要的步进位置。通过绕线的电流方向还可反向。

全步和半步：步进驱动器控制步进电机的运行方式，步进电机常用的励磁模式有全步、半步和微步三种。这些励磁模式对电机提供的运行特性和扭矩都有影响。每次将输入脉冲施加到电机时，步进电机都会将电子信号转换为机械运动。每个脉冲以固定增量移动轴。如果步进电机的步进分辨率为1.8°，那么为了让轴旋转一整圈，在全步进操作中，步进电机需要接收200个脉冲，360°÷1.8=200。 有两种全步励磁模式： 在单相全步中，电机一次仅在一个相通电的情况下运行。在任何激励模式中，这种模式需要来自驱动器的最少功率。

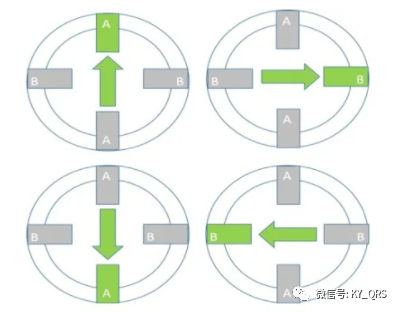
在双相全步中，电机在两相同时通电的情况下运行。此模式提供了改进的扭矩和速度性能。两相开启比单相开启提供大约30%到40%的扭矩，但它需要来自驱动器的两倍功率。

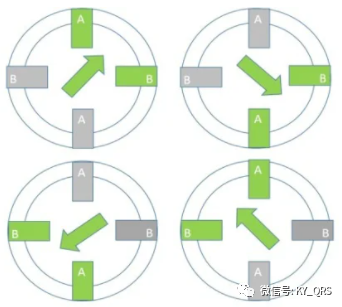
半步励磁模式是一相开启和两相开启全步模式的组合。这导致基本步距角的一半。由于角度分辨率的提高，这个较小的步距角提供了更平滑的操作。半步产生的转矩比两相全步低约15%，但修改后的半步通过增加单相通电时施加到电机的电流来消除转矩降低。

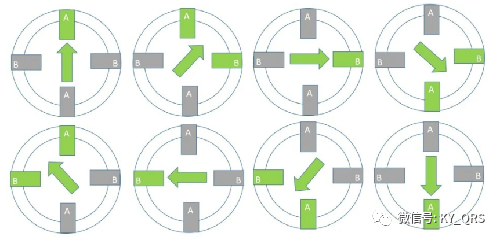
微步可实现更好的控制和更平稳的操作： 微步可以将电机的基本步长分割多达256倍，使小步距变小。微型驱动器使用两个相隔90°的电流正弦波，这非常适合实现电机的平稳运行。您会注意到电机运行安静，没有真正可检测到的步进动作。

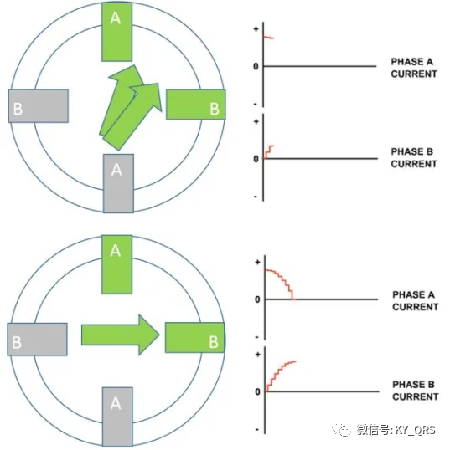
通过控制每个绕组中电流的方向和幅度，分辨率提高，电机特性改善，振动更小，运行更平稳。因为正弦波一起工作，所以从一个绕组到另一个绕组的平滑过渡。当一个电流增加时，另一个电流减小，从而实现平稳的步进进展并保持扭矩输出。 细分的原理和输出控制：

一个理想的步进电机电流曲线应该是相位相差90度的正弦曲线如下图：

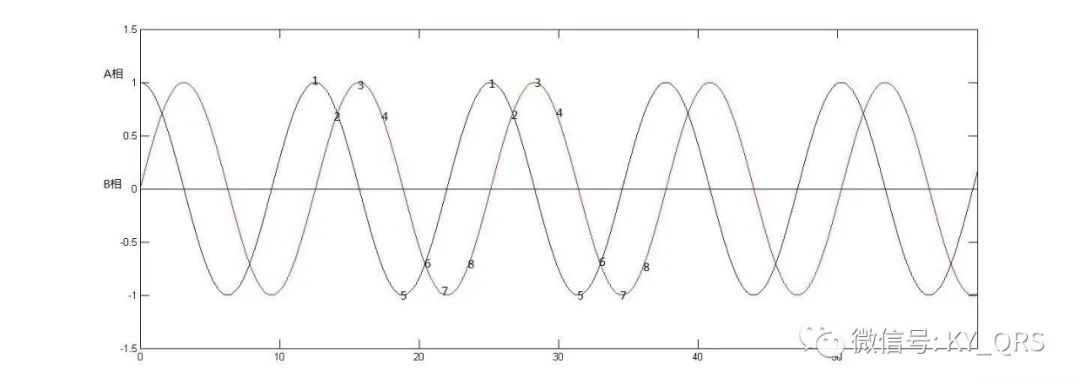
图中蓝色线时A相电流，红色线是B相电流。如果把A相正负极值视为A+A-，B相正负极值视为B+B-，比较一下四拍方式正转A+B+A-B-和反转A+B-A-B+不难看出四排方式实际上是用一个脉冲来代替一个正弦半周期，相位点从左到右变化则电机正转，从右到左电机反转。类似的我们把八拍方式A+;A+B+;B+;B+A-;A-;A-B-;B-;B-A+;放到曲线里也可以找到对应点，图中标出了各拍的相位点1，2，3…，不难看出用A+B+代替第2拍点用B+A-代替第四拍点都是近似的做法。那么这种近似和理想情况的电流的差值去哪里了呢？这些电流被无谓的消耗掉了而且多余的电流会引起电机转动的不平稳。为什么要细分呢？实际细分的终极目标就是在正弦的周期中插入若干个点使得相电流接近正弦变化，细分可以提高定位精度和电机运转的平稳性。

spwm运算和输出 Spwm的产生可以分为软件方法和硬件方法，硬件方法通过硬件产生一路三角波一路正弦波，经过一个比较器比较正弦波幅值与三角波幅值的关系即可得到spwm波。这种方法也应用于很多spwm集成芯片。硬件方法在波形产生上不需要软件参与，并且调频和调幅控制上都是比较简单的。硬件方法的功能和性能取决于芯片本身，对于比较复杂的应用上会受到限制。 软件方法的思路是使得pwm波以spwm的脉宽数据变化滤波后就可以得到正弦波形，通过计算得到占空比的波形数据，按波形数据调整pwm。其实软方法和硬方法也并不是绝对的，比如ti的dsp芯片内部的spwm发生器，他的做法是在内存中存储一张正弦表，然后用一个和定时器时钟同步的计数器正负计数模拟一个三角波，每个时钟将正弦表的值与三角计数值作比较输出即得到spwm，实际上可以看成是一种半软件半硬件的做法。软件方法的优势在于成本低且更灵活，成本低不用说了，灵活性上举个例子：调制正弦波性的极性是由独立的控制位实现的（双极性），如果输出标准的正弦波形硬方法需要三角波发生器和正弦波发生器的起始点精确对齐，这在硬件电路实现上需要附带锁相环电路才能保证，而软件方法则不需要任何附加操作。现在为了改善步进电机的驱动性能，我们希望极性翻转点落后输出几个微秒，要做到这一点硬件方法改动肯定是难上难，而软件方法上只需要增加个定时滞后输出就行了。 为了减少运算开销也可以使用查表法，把计算好的spwm数据存储在rom里，按顺序输出表中的值即可。这种方法的数据计算可以在pc机上通过matlab软件进行，将数据算好粘贴到源程序中就可以了。查表法的局限在于参数的变化和存储开销的矛盾，参数越复杂占用存储空间越大。 (1)三角波向锯齿波的转换 载波为三角波时输出的是一个左右不对称的pwm波形，只有这种波形能够调制出半周期对称的正弦波，这种方法称为非对称的自然采样法。其它方法（规则采样等效面积…）都是为了减小计算量或不得以而采取的近似方法。非对称pwm开点与关闭点没有必然关系，必须由中央对齐的pwm模式通过一个周期的两次更新来输出。三角波可以看成是两个锯齿波的组合，因此我们可以通过锯齿波的数据来简化程序结构。我们比较下面三张图：

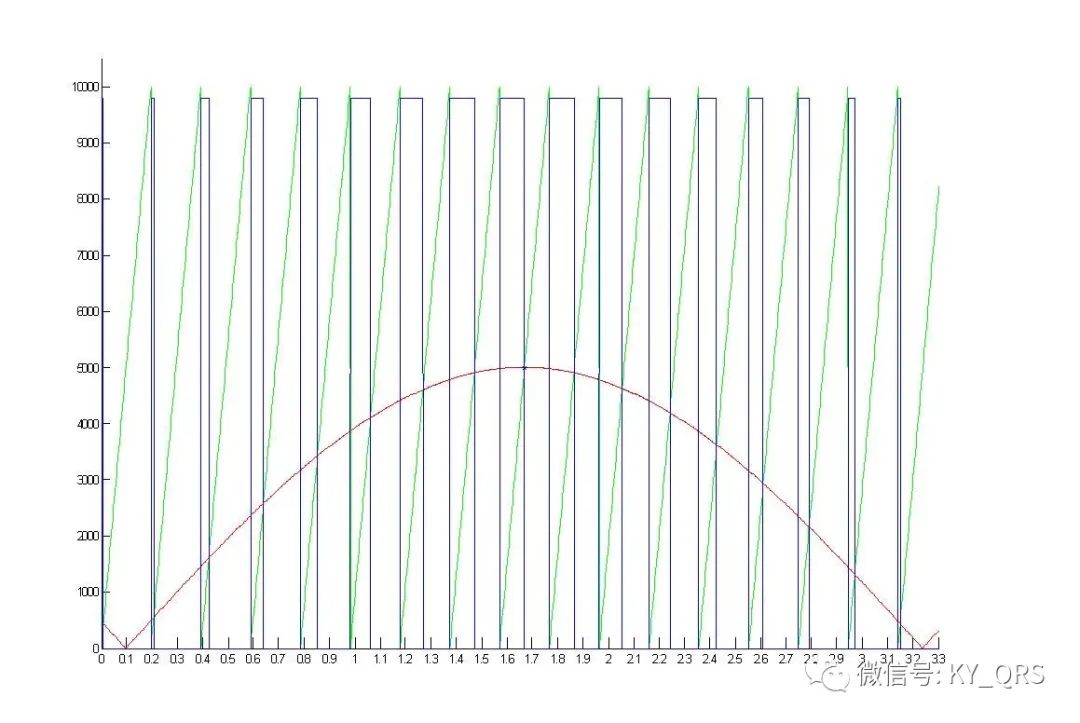
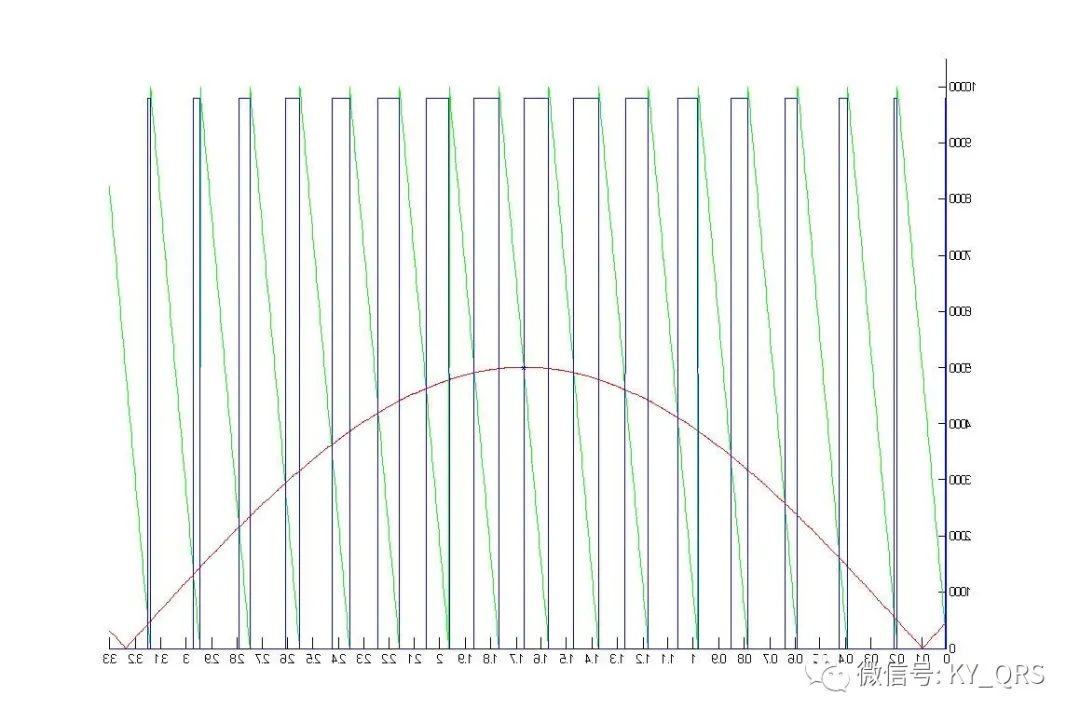
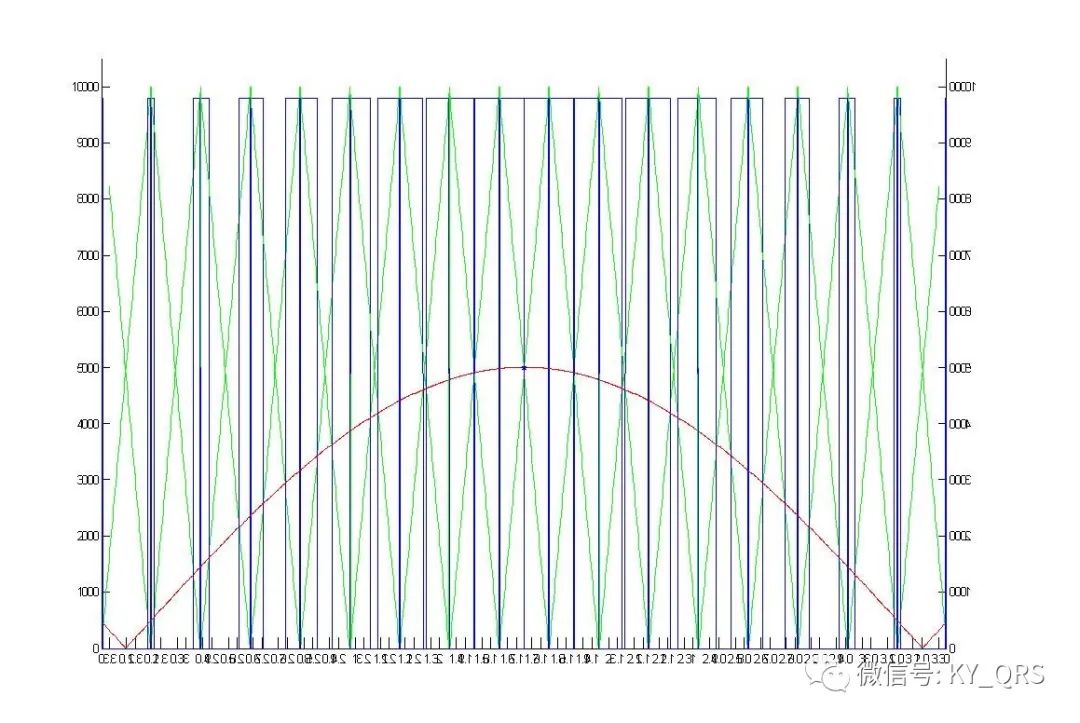
图1是一个锯齿波幅值为1，载波比N=16，正弦幅值0.5，正弦与锯齿波相差为半个锯齿波周期；图2是图1水平翻转的结果；图3是图1和图2的叠加结果。图三中看到三角波形的spwm数据了吗？没错就这么简单，锯齿波正弦幅值比为2：1，相差半个锯齿波周期，计算出来的数据首尾组合成三角波数据。算法上就很简单了，假设数组中存放上述的锯齿波spwm数据，编号0~15共16个，依次取0，1，2，…15为三角波形开点输出数据，则反向取15，14，13，…0为三角波形关点数据即可。特别的如果载波比为奇数时三角波也为奇数，中间的数自然和自己组合的数据仍然是正确的。 注意这里提及的方法可以把三角波形的计算转换为锯齿波，但并不能减少计算量，因为如果是偶数个三角波只要计算四分之一周期就够了其他的是对称的，而锯齿波形数据需要计算半个周期。至此我们可以使用锯齿波的方法计算按三角波的数据输出。 (2)spwm迭代运算 为计算spwm占空比首先要求得锯齿波斜线与正弦交点，即方程KX+B=Y与Sin(X)=Y的解。这个方程是一个超越方程，只能通过迭代的方法计算。我们将直线方程变为X=(Y-B)/K，首先任取一个X值（这个值就是迭代初值），将它带入Sin(X)求一个Y值再将Y值代入(Y-B)/K求一次X值，再将X带入Sin(X)求一个Y值…如此反复若干次后可以得到一个结果就是方程式的解，这个就叫做迭代法。迭代次数越多；迭代初值越接近结果精度越高。每一组数据计算有这样几个参数1：正弦幅值（三角幅值与之成比例）2：载波比N值即半周期中三角波个数。另外pwm的占空比即定时器的通道值是和pwm的周期值有关系的，因此为了计算定时器通道值还需要一个周期值，对于stm32f这个值就是定时器ARR寄存器的值，它决定pwm周期（或频率）。附件中有个matlab_spwm.rar，matlab下计算定时器spwm数值和绘图的小工具上面几个图就是用它画的，开始部分可以置参数 s_M=32768/65536 %正弦波幅值比0~1 s_N=16 %半周期三角波个数 s_Pre=16384 %单片机定时器模数值 执行分为三部分，计算spwm数据；将数据按周期值换算为定时器设定值；画图；
计算定时器设定结果在TimerSetting中，复制粘贴替换tab字符成逗号就行了，下面是上述参数的计算结果： 1780 5246 8444 11221 13461 15088 16063 16384 16075 15182 13764 11893 9645 7102 4346 1463 (3)spwm实时运算的优化 如前所述简单的应用查表法就可以解决了但是复杂一点的功能就不能满足要求了，比如步进电机大范围调速、不同转速下恒力矩输出、恒加速运动等等。网上有很多文章介绍自然采样法的数学方法，并给出了各种优化算法，这些算法力图精确求解三角方程与正弦方程的交点，由于运算中带有大量的浮点运算若没有dsp或高速浮点处理芯片的支持必然会造成运算时间过长对实时调控产生影响。实际上我们需要的计算精度和每载波周期可能的开关点数量有关系，此数值用C来表示，称其为控制比数值上=载波周期/pwm周期，同步调制方式中此值为整数，可以理解为用多少个pwm周期控制一个载波周期。pwm频率实际上是开关电路的极限频率或最理想工作的频率，假设每载波周期可能的开关点数量为512个则需要二进制的9位计算精度如果再加一位存疑位最多计算10位就够了。如果采用数据类型IEEE32浮点数迭代运算将得到24位（二进制）精度的计算结果，与实际需要相差甚远,也就是说你算了半天大部分是没有意义的计算,这种计算资源浪费发生在每一次运算中,因此累计起来就比较惊人了。从另一个角度看由于pwm频率的限制有高精度的计算结果也无法实施高精度的开关控制,这么说就好理解了。对计算采取一定的优化是必须的它将直接影响系统的实时性能。 步进电机运行控制 至此假设我们可以很快的在单片机上进行实时的迭代运算了。迭代计算一个半周期的spwm其输入的原始参数只和三个数值有关:
1.M正弦的幅值这个值将决定步进电机的相电流大小,也就是步进电机的输出力矩。步进电机的优点之一是它的低速性能,当步进电机低速运转时转子始终受到磁场力的牵引转动,这个力的大小直接取决于励磁电流的大小,很小的速度下却可以用很大的力牵引转动。而直流电机的低速运动只能靠减小励磁电流实现,实际上就是小力矩实现低速,这样控制就不可能很精确特别是启停阶段尤其麻烦。步进电机在高速时力矩下降很快这个原因也不难理解,因为在步进电机励磁线圈里有多组磁极快速划过产生很大的感生电动势抵消了驱动的电压致使励磁电流变小力矩变小。为了改善高速性能解决办法只有一个提高工作电压。根据电机转速自动调整相电流的大小就可以实现恒定的力矩输出了,即低转速小幅值高转速大幅值。 2.载波比N和控制比C,这两个参数和调制频率F的关系是: F*2C*2N=TF(TF是定时器的时钟频率) 我们慢慢来解释一下这个式子,调制频率就是我们实际想要的电机转速,从上面式子可以看出要让电机速度增加有两个方法即减小C或减小N(TF也是可以变的暂不考虑); C实际上就是定时器的模数值(ARR),他的含义是使用几个定时器时钟周期产生一个pwm周期,前面的2是由于定时器工作在中央对齐模式下,定时器+-计数一轮产生一个完整的三角波周期。ARR的取值范围不可以太小,因为需要定时器中断来更新个通道的值,太小的数值两次更新时间过短而无法实现计算和更新步计数等操作。ARR的值如果太大则输出的pwm频率过低效果不佳。 N是载波比也就是半周期的三角波的数量,他的含义是使用几个pwm周期调制出一个正弦周期,其实也就是我们常说的细分数,它决定一个正弦周期(一个步距角)内可以控制的位置点的数量。在常见的驱动器中这个数值都是由拨码开关事先设定的,工作中是一个固定值,原因是硬件电路无缝的调整细分度几乎是不可能的。软件运算则没有这个问题,N的取值可以是任意的，唯一受影响的就是极性控制，上面算式里N前面的2含义是正弦正半周期和负半周期。N的取值还要考虑内存和计算占用；迭代算法如果有接近结果的初始值将使得运算效率大幅提高，因此对于有初始值的运算每一个计算点都要有存储空间占用，过大的N值要考虑内存资源，如果无初值的计算则要考虑计算资源。特别的当N值变化时初值会与真实值有差距，所以应尽量减少N的变动。 步值计数产生AB极性逻辑和正反转：
先来梳理一下目前已经现在做到的内容，内存中有一个数组存放整个正弦半周期的实时运算的spwm数据，这个数据是根据当前的pwm周期折算过，因此每个pwm周期依次将数组内容赋值给定时器通道值就可以在定时器通道管脚输出正弦变化的pwm了。另外使用一个（l6205是两个，也可以用非门）io口来控制极性输出，比如高电平输出正弦负半周，低电平输出正弦正半周。
接下来需要安排一个合理而简单的数据结构把步进计数、细分和极性控制合为一体。首先我们用一个s32 stepcounter全局量来做步进计数,它的数值与步进电机的实时位置对应，这个变量是一个很关键的变量，因为任意时刻的AB两相spwm数据输出点和极性控制信号都由它产生。假设我们把它的低八位视为细分步计数（256为最大细分）,则这个计步值除256对应整步位置。另外安排一个u8 microstep用来控制细分步进,它的取值和当前的细分度有关，如果256细分则microstep=1,128细分microstep=2,以此类推.如果电机正转前进一个微步则stepcounter+=microstep，如果反转一个微步则stepcounter-=microstep（微步进这部分可以放到中断程序里），OK正反转很简单，微步前进自动更新整步。关键点在于如何使用这个计数值产生两个相位的极性信号输出控制和A相B相的spwm数据位置，这里解释一下为什么会希望控制都由这一个变量产生：因为这样的程序最简单，虽然这里讲一大堆但是在编程实现时你就看到了就几行搞定；不容易出错，效率最高，你可以想象的到如果涉及的变量越多操作的代码越多需要考虑的可能性越多也越容易错；便于封装和功能扩展，比如你想做一个AD采样值与电机位置按一个比例同步的程序即转滑阻电机跟着动的小玩意儿，稍微改改把AD采样值赋给计步值其它都不用管了。
先说第一个数据的输出，spwm数组256个，如果不考虑极性则数据位置只和stepcounter的低8位有关，因此A相数据用stepcounter的低8位作指针从数组取数就可以（A相0值点为计步0值点），B相与A相相差为90度，所以A=0，1，2，255，0 则B=128，129，130，127，128能看出来吗？（A的数据指针+128）%256等同于 A的数据指针^128就是B的数据指针。
程序上这样写：
A通道值=spwm数组[（u8）stepcounter]；
B通道值=spwm数组[（u8）stepcounter^128]；
这里数组大小是256，所以一个逻辑异或就解决，如果你非要取大小是100个的话你就得（point+50）%100才能找到B相位点了。 步进电机基本算法，S算法：

为了实现步进电机的平缓启停以及避免转高转速时不失步停转。在步进电机启动、停止过程中，需要采用加减速的算法对启动过程进行控制。S曲线是加减速控制最理想的方案。但是S曲线的公式以及控制过程都比较复杂。

将S曲线离散化，在整个加减速过程中，以一定的时间间隔更新频率，总的更新次数为2*N，i表示为第i次的更新，则第i次更新的频率f(i)表示为：

其中fb为开始的频率，fr是最终运行的频率，α是曲线的伸缩系数，一般可以取3-5之间的常数。

比如，启动加速，开始频率为400Hz，运行频率为5KHz。

停止减速，开始频率为5KHz，停止频率为400Hz，

加减速的时间均为1s，按10ms的时间间隔更新频率，总共更新100次，α取5。

通过以下步骤实现实现步进电机的S曲线的加减速控制：

配置1ms的定时器以及1ms的中断程序在中断程序中对加减速的频率更新次数i进行计数配置产生步进电机驱动信号的PWM模块，设置PWM的定时中断以及中断程序在PWM的定时中断程序中，计算当前更新次数对应的频率，并按出来的频率更新PWM的频率以及占空比在PWM的定时中断程序中，计算步进电机运行的步数，如果达到设置的步数减去停止的S曲线减速运行所设置的步数，则开始减速运行。同时检测外部输入，如果有需要停止运行的输入条件，则开始减速运行。

整个加减速控制过程的难点在于：

步进电机的计步以及频率更新需要在每一个PWM中断中进行。步进电机的运行频率最高到40KHz，这种频率下，PWM的定时中断周期达到了25us，PWM定时器中断程序运行总时间尽量小，根据经验至少小于中断周期的30%，即7.5us。一旦超过这个数值，导致所有中断程序（包括PWM定时中断程序）漏运行，基本主程序无法运行，导致整个控制器假死现象。根据S曲线的公司是一个复杂的非线性的指数浮点数运算，需要耗费大量的时间，直接调用C语言的库函数计算这一数值可能耗费几十上百毫秒。

为了解决S曲线的运算时间问题，基于STM32F103，我采用了查表法，具体步骤如下：

1. 将α值定义5，

的取值范围为-5~5之间。

2. 在整个加减速过程中，表达式

在取值范围-5~5内均匀取1024个数值，得到数值表。

3. 定义一个unsigned short型有1024个元素的const类型的数组，用于存储数值表。

4. Const数组存储在内部的flash，数值表共占用2048字节。

STM32F103RTC6共256K，程序组和设置参数占用48K，bootloader程序占用了8K，远程升级空间占用了100K，目前应用程序只用到40K左右。

剩余60K左右的空间，腾出2K的空间来存储数值表，有空间，就是这么任性。

5. 在中断程序中，根据总的更新次数以及当前的更新计数值，计算

值，再映射到0-1023的数值有的索引值，通过索引获取数值。

6. 需要注意的是stm32f103不支持浮点数的运算，所以对于浮点数的运算，需要换算成乘以一个数再除以另一个数，比如*α，需要转变为*65535/13107。

下面一段代码是根据更新的计数值获取频率的函数：

U16 fnMC_GetFreq(U16 n, U16 halftn, U16 alpha, U16 minfreq, U16 maxfreq){//alpha=alpha * 4096

signed int udataA;

signed short uiDataA;

U16 uiRes;

U32 uwData;

udataA=(signed int)alpha * (signed int)n;

udataA=(signed int)udataA / halftn;

if(udataA > 32767){

udataA=32767;

}

uiDataA=(signed short)alpha - (signed short)udataA;

uiDataA=(signed short)4 * 4096 - uiDataA;

if(uiDataA < 0){

uiDataA=0;

}

uiRes=(U16)uiDataA;

uiRes=uiRes / 32;//*1023/8/4096

if(uiRes > 1023){

uiRes=1023;

}

udataA=(signed int)(maxfreq - minfreq) * g_mc_uchExp[uiRes];

udataA=udataA / 65535;

uiDataA=(signed int)udataA;

uiDataA +=minfreq;

if(uiDataA < 200){

uiDataA=200;

}

return(uiDataA);

}

下面一段代码是产生步进电机控制信号的PWM周期中断程序：

int data;

U16 freq;

STRMotorRegs *motor;

motor=&g_motor_regs[0];

MOTOR_A_CLEARINT();

motor->steps ++;

data=(int)MOTOR_A_STEPS_GET();

if(motor->direction==0)

{

data=data + 1;

}

else

{

data=data - 1;

}

MOTOR_A_STEPS_SET(data);

freq=motor->runfrequency;

if(motor->runstate==MOTOR_RUN_STATE_INC){

if(motor->runtimer >=motor->starttime){

motor->runstate=MOTOR_RUN_STATE_IDLE;

}else{

freq=fnMC_GetFreq(motor->runtimer, motor->halfstarttime, motor->alpha, motor->startfreq, motor->runfrequency);//U16 n,U16 halftn,U16 alpha,U16 maxfreq,U16 minfreq)

}

motor->runsnapfreq=freq;

}else if(motor->runstate==MOTOR_RUN_STATE_IDLE){

if(motor->totalstep <=(motor->steps + motor->stopremainstep)){

motor->runstate=MOTOR_RUN_STATE_DEC;

motor->runtimer=0;

}

motor->runsnapfreq=freq;

}else{

if(motor->runtimer >=motor->stoptime){

freq=motor->stopfreq;

}else{

freq=fnMC_GetFreq(motor->runtimer, motor->halfstoptime, motor->alpha, motor->runsnapfreq, motor->stopfreq);//U16 n,U16 halftn,U16 alpha,U16 maxfreq,U16 minfreq)

}

}

if(motor->steps >=motor->totalstep)

{

motor->starting=FALSE;

}

if(FALSE==motor->starting)

{

MOTOR_A_DISABLE();

}else{

motor->curfrequency=freq;

fnMT_Cal_MotorA_TimeConf();

}

下面是生成S曲线数值表、控制步进电机启动、停止的视频，从视频上可以明显看到启动时慢加速->快加速->慢加速的过程，以及停止时慢减速->快减速->慢减速的过程。

部分程序代码（需要代码可以下载完整程序）

审核编辑 ：李倩