作者 | Victor Zhou
有个事情可能会让初学者惊讶:神经网络模型并不复杂!『神经网络』这个词让人觉得很高大上,但实际上神经网络算法要比人们想象的简单。
这篇文章完全是为新手准备的。我们会通过用Python从头实现一个神经网络来理解神经网络的原理。本文的脉络是:
介绍了神经网络的基本结构——神经元;
在神经元中使用S型激活函数;
神经网络就是连接在一起的神经元;
构建了一个数据集,输入(或特征)是体重和身高,输出(或标签)是性别;
学习了损失函数和均方差损失;
训练网络就是最小化其损失;
用反向传播方法计算偏导;
用随机梯度下降法训练网络。
砖块:神经元
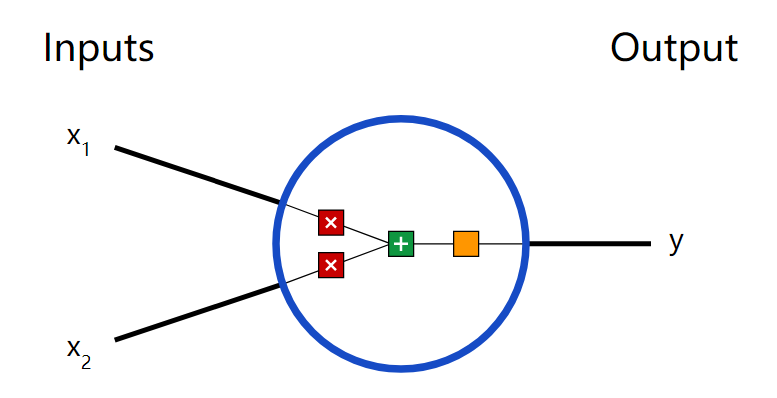
首先让我们看看神经网络的基本单位,神经元。神经元接受输入,对其做一些数据操作,然后产生输出。例如,这是一个2-输入神经元:
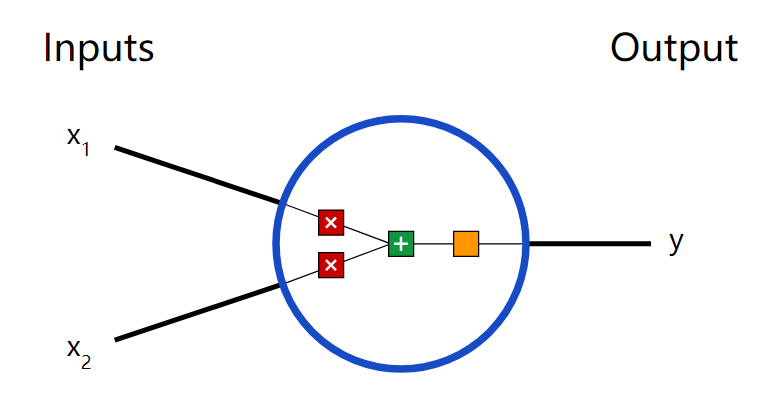
这里发生了三个事情。首先,每个输入都跟一个权重相乘(红色):
然后,加权后的输入求和,加上一个偏差b(绿色):
最后,这个结果传递给一个激活函数f:
激活函数的用途是将一个无边界的输入,转变成一个可预测的形式。常用的激活函数就就是S型函数:
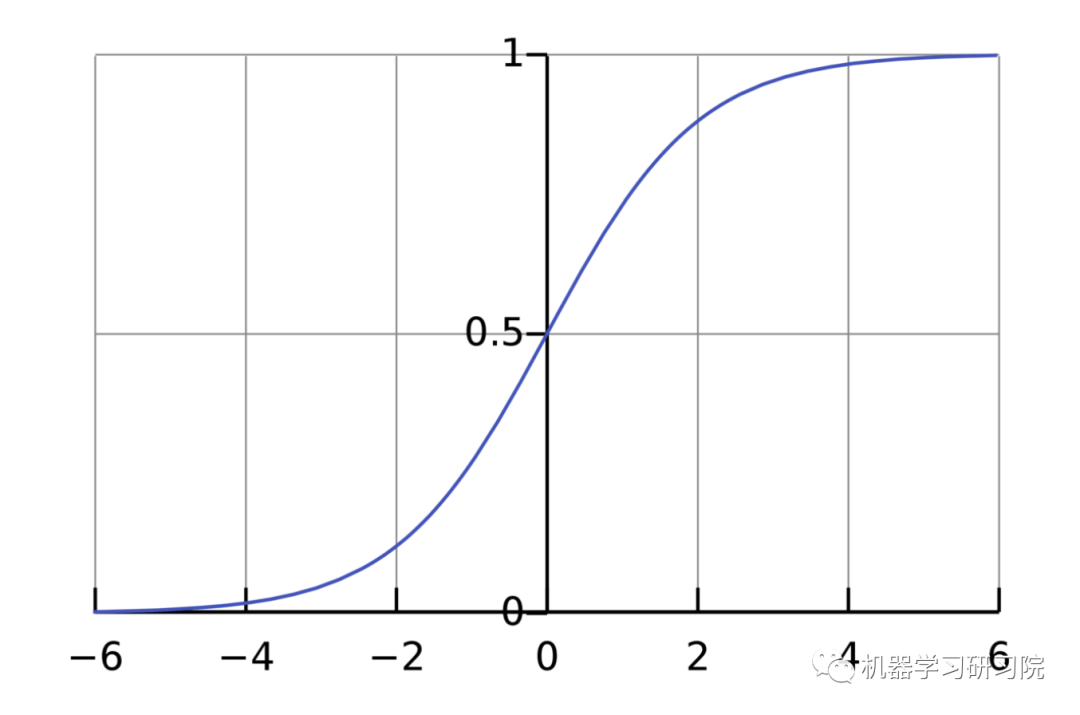
S型函数的值域是(0, 1)。简单来说,就是把(−∞, +∞)压缩到(0, 1) ,很大的负数约等于0,很大的正数约等于1。
一个简单的例子
假设我们有一个神经元,激活函数就是S型函数,其参数如下:
就是以向量的形式表示。现在,我们给这个神经元一个输入。我们用点积来表示:
当输入是[2, 3]时,这个神经元的输出是0.999。给定输入,得到输出的过程被称为前馈(feedforward)。
编码一个神经元
让我们来实现一个神经元!用Python的NumPy库来完成其中的数学计算:
importnumpyasnp defsigmoid(x): #我们的激活函数:f(x)=1/(1+e^(-x)) return1/(1+np.exp(-x)) classNeuron: def__init__(self,weights,bias): self.weights=weights self.bias=bias deffeedforward(self,inputs): #加权输入,加入偏置,然后使用激活函数 total=np.dot(self.weights,inputs)+self.bias returnsigmoid(total) weights=np.array([0,1])#w1=0,w2=1 bias=4#b=4 n=Neuron(weights,bias) x=np.array([2,3])#x1=2,x2=3 print(n.feedforward(x))#0.9990889488055994
还记得这个数字吗?就是我们前面算出来的例子中的0.999。
把神经元组装成网络
所谓的神经网络就是一堆神经元。这就是一个简单的神经网络:
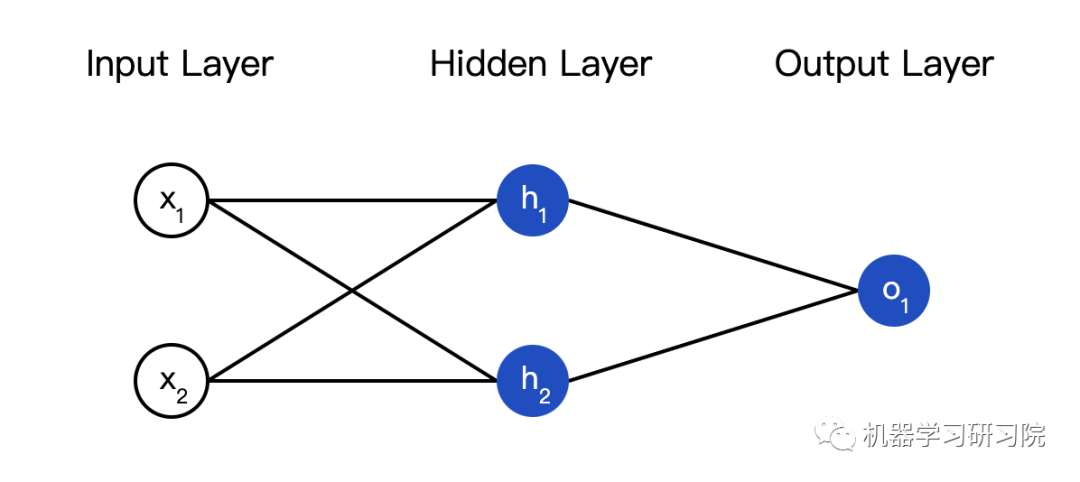
这个网络有两个输入,一个有两个神经元(和)的隐藏层,以及一个有一个神经元() )的输出层。要注意,的输入就是和的输出,这样就组成了一个网络。
隐藏层就是输入层和输出层之间的层,隐藏层可以是多层的。
例子:前馈
我们继续用前面图中的网络,假设每个神经元的权重都是,截距项也相同,激活函数也都是S型函数。分别用表示相应的神经元的输出。
当输入时,会得到什么结果?
这个神经网络对输入的输出是0.7216,很简单。
一个神经网络的层数以及每一层中的神经元数量都是任意的。基本逻辑都一样:输入在神经网络中向前传输,最终得到输出。接下来,我们会继续使用前面的这个网络。
编码神经网络:前馈
接下来我们实现这个神经网络的前馈机制,还是这个图:
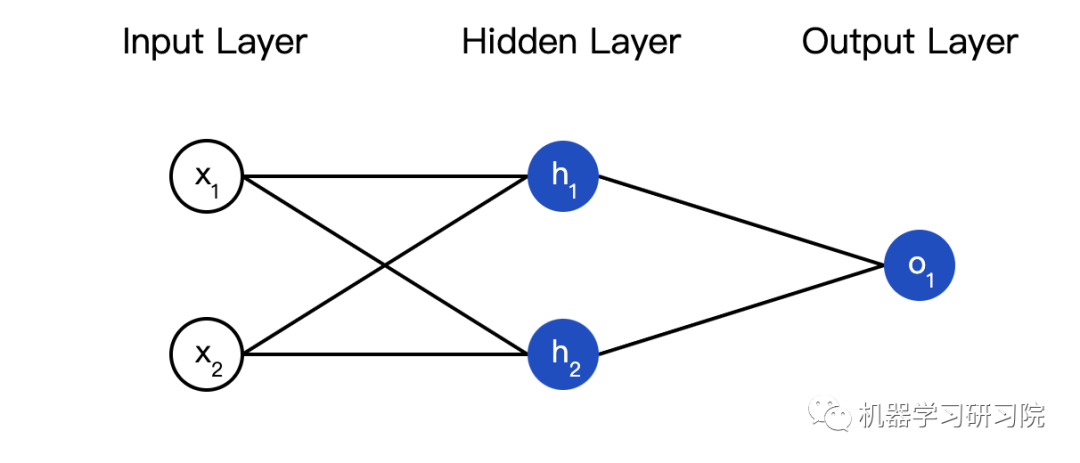
importnumpyasnp #...codefromprevioussectionhere classOurNeuralNetwork: ''' Aneuralnetworkwith: -2inputs -ahiddenlayerwith2neurons(h1,h2) -anoutputlayerwith1neuron(o1) Eachneuronhasthesameweightsandbias: -w=[0,1] -b=0 ''' def__init__(self): weights=np.array([0,1]) bias=0 #这里是来自前一节的神经元类 self.h1=Neuron(weights,bias) self.h2=Neuron(weights,bias) self.o1=Neuron(weights,bias) deffeedforward(self,x): out_h1=self.h1.feedforward(x) out_h2=self.h2.feedforward(x) #o1的输入是h1和h2的输出 out_o1=self.o1.feedforward(np.array([out_h1,out_h2])) returnout_o1 network=OurNeuralNetwork() x=np.array([2,3]) print(network.feedforward(x))#0.7216325609518421
结果正确,看上去没问题。
训练神经网络 第一部分
现在有这样的数据:
| 姓名 | 体重(磅) | 身高 (英寸) | 性别 |
|---|---|---|---|
| Alice | 133 | 65 | F |
| Bob | 160 | 72 | M |
| Charlie | 152 | 70 | M |
| Diana | 120 | 60 | F |
接下来我们用这个数据来训练神经网络的权重和截距项,从而可以根据身高体重预测性别:
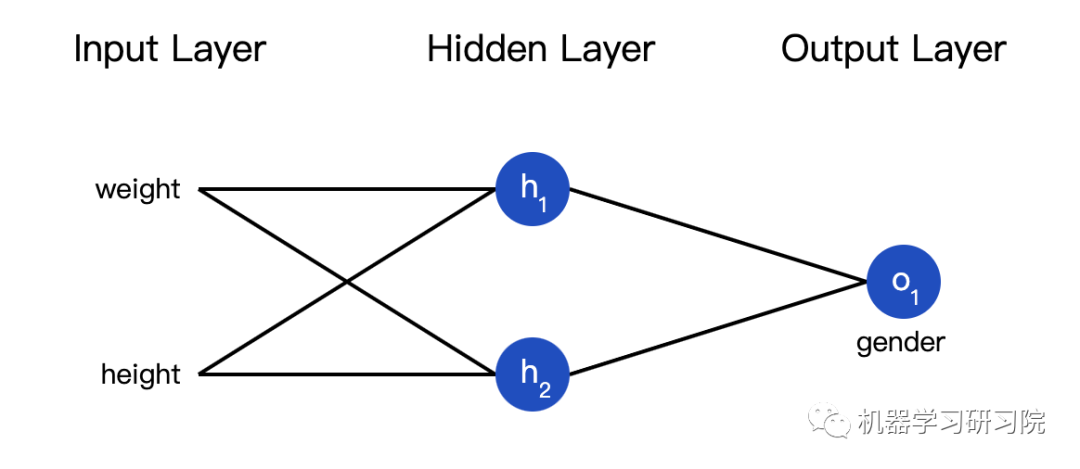
我们用0和1分别表示男性(M)和女性(F),并对数值做了转化:
| 姓名 | 体重 (减 135) | 身高 (减 66) | 性别 |
|---|---|---|---|
| Alice | -2 | -1 | 1 |
| Bob | 25 | 6 | 0 |
| Charlie | 17 | 4 | 0 |
| Diana | -15 | -6 | 1 |
我这里是随意选取了135和66来标准化数据,通常会使用平均值。
损失
在训练网络之前,我们需要量化当前的网络是『好』还是『坏』,从而可以寻找更好的网络。这就是定义损失的目的。
我们在这里用平均方差(MSE)损失:,让我们仔细看看:
是样品数,这里等于4(Alice、Bob、Charlie和Diana)。
表示要预测的变量,这里是性别。
是变量的真实值(『正确答案』)。例如,Alice的就是1(男性)。
变量的预测值。这就是我们网络的输出。
被称为方差(squared error)。我们的损失函数就是所有方差的平均值。预测效果越好,损失就越少。
更好的预测 = 更少的损失!
训练网络 = 最小化它的损失。
损失计算例子
假设我们的网络总是输出0,换言之就是认为所有人都是男性。损失如何?
| Name | y_true | y_pred | (y_true - y_pred)^2 |
|---|---|---|---|
| Alice | 1 | 0 | 1 |
| Bob | 0 | 0 | 0 |
| Charlie | 0 | 0 | 0 |
| Diana | 1 | 0 | 1 |
代码:MSE损失
下面是计算MSE损失的代码:
importnumpyasnp defmse_loss(y_true,y_pred): #y_trueandy_predarenumpyarraysofthesamelength. return((y_true-y_pred)**2).mean() y_true=np.array([1,0,0,1]) y_pred=np.array([0,0,0,0]) print(mse_loss(y_true,y_pred))#0.5
如果你不理解这段代码,可以看看NumPy的快速入门中关于数组的操作。
好的,继续。
训练神经网络 第二部分
现在我们有了一个明确的目标:最小化神经网络的损失。通过调整网络的权重和截距项,我们可以改变其预测结果,但如何才能逐步地减少损失?
这一段内容涉及到多元微积分,如果不熟悉微积分的话,可以跳过这些数学内容。
为了简化问题,假设我们的数据集中只有Alice:
假设我们的网络总是输出0,换言之就是认为所有人都是男性。损失如何?
| 姓名 | 体重 (减 135) | 身高 (减 66) | Gender |
|---|---|---|---|
| Alice | -2 | -1 | 1 |
那均方差损失就只是Alice的方差:
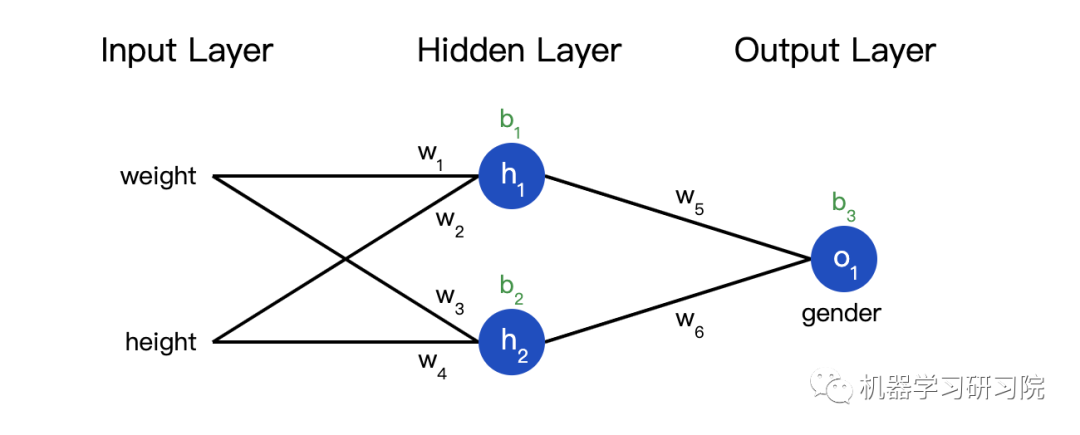
也可以把损失看成是权重和截距项的函数。让我们给网络标上权重和截距项:

这样我们就可以把网络的损失表示为:
假设我们要优化,当我们改变时,损失会怎么变化?可以用来回答这个问题,怎么计算?
接下来的数据稍微有点复杂,别担心,准备好纸和笔。
首先,让我们用来改写这个偏导数:
因为我们已经知道,所以我们可以计算
现在让我们来搞定。分别是其所表示的神经元的输出,我们有:
由于只会影响(不会影响),所以:
对,我们也可以这么做:
在这里,是身高,是体重。这是我们第二次看到(S型函数的导数)了。求解:
稍后我们会用到这个。
我们已经把分解成了几个我们能计算的部分:
这种计算偏导的方法叫『反向传播算法』(backpropagation)。
好多数学符号,如果你还没搞明白的话,我们来看一个实际例子。
例子:计算偏导数
我们还是看数据集中只有Alice的情况:
| Name | |||
|---|---|---|---|
| Alice | 1 | 0 | 1 |
| 姓名 | 身高 (minus 135) | 体重 (minus 66) | Gender |
|---|---|---|---|
| Alice | -2 | -1 | 1 |
把所有的权重和截距项都分别初始化为1和0。在网络中做前馈计算:
网络的输出是,对于Male(0)或者Female(1)都没有太强的倾向性。算一下
提示:前面已经得到了S型激活函数的导数。
搞定!这个结果的意思就是增加也会随之轻微上升。
训练:随机梯度下降
现在训练神经网络已经万事俱备了!我们会使用名为随机梯度下降法的优化算法来优化网络的权重和截距项,实现损失的最小化。核心就是这个更新等式:
是一个常数,被称为学习率,用于调整训练的速度。我们要做的就是用减去
如果是正数,变小,会下降。
如果是负数,会变大,会上升。
如果我们对网络中的每个权重和截距项都这样进行优化,损失就会不断下降,网络性能会不断上升。
我们的训练过程是这样的:
从我们的数据集中选择一个样本,用随机梯度下降法进行优化——每次我们都只针对一个样本进行优化;
计算每个权重或截距项对损失的偏导(例如、等);
用更新等式更新每个权重和截距项;
重复第一步;
代码:一个完整的神经网络
我们终于可以实现一个完整的神经网络了:
| 姓名 | 身高 (减 135) | 体重 (减 66) | Gender |
|---|---|---|---|
| Alice | -2 | -1 | 1 |
| Bob | 25 | 6 | 0 |
| Charlie | 17 | 4 | 0 |
| Diana | -15 | -6 | 1 |
importnumpyasnp defsigmoid(x): #Sigmoidactivationfunction:f(x)=1/(1+e^(-x)) return1/(1+np.exp(-x)) defderiv_sigmoid(x): #Derivativeofsigmoid:f'(x)=f(x)*(1-f(x)) fx=sigmoid(x) returnfx*(1-fx) defmse_loss(y_true,y_pred): # y_true和y_pred是相同长度的numpy数组。 return((y_true-y_pred)**2).mean() classOurNeuralNetwork: ''' Aneuralnetworkwith: -2inputs -ahiddenlayerwith2neurons(h1,h2) -anoutputlayerwith1neuron(o1) ***免责声明***: 下面的代码是为了简单和演示,而不是最佳的。 真正的神经网络代码与此完全不同。不要使用此代码。 相反,读/运行它来理解这个特定的网络是如何工作的。 ''' def__init__(self): #权重,Weights self.w1=np.random.normal() self.w2=np.random.normal() self.w3=np.random.normal() self.w4=np.random.normal() self.w5=np.random.normal() self.w6=np.random.normal() #截距项,Biases self.b1=np.random.normal() self.b2=np.random.normal() self.b3=np.random.normal() deffeedforward(self,x): # X是一个有2个元素的数字数组。 h1=sigmoid(self.w1*x[0]+self.w2*x[1]+self.b1) h2=sigmoid(self.w3*x[0]+self.w4*x[1]+self.b2) o1=sigmoid(self.w5*h1+self.w6*h2+self.b3) returno1 deftrain(self,data,all_y_trues): ''' -dataisa(nx2)numpyarray,n=#ofsamplesinthedataset. -all_y_truesisanumpyarraywithnelements. Elementsinall_y_truescorrespondtothoseindata. ''' learn_rate=0.1 epochs=1000#遍历整个数据集的次数 forepochinrange(epochs): forx,y_trueinzip(data,all_y_trues): #---做一个前馈(稍后我们将需要这些值) sum_h1=self.w1*x[0]+self.w2*x[1]+self.b1 h1=sigmoid(sum_h1) sum_h2=self.w3*x[0]+self.w4*x[1]+self.b2 h2=sigmoid(sum_h2) sum_o1=self.w5*h1+self.w6*h2+self.b3 o1=sigmoid(sum_o1) y_pred=o1 #---计算偏导数。 #---Naming:d_L_d_w1represents"partialL/partialw1" d_L_d_ypred=-2*(y_true-y_pred) #Neurono1 d_ypred_d_w5=h1*deriv_sigmoid(sum_o1) d_ypred_d_w6=h2*deriv_sigmoid(sum_o1) d_ypred_d_b3=deriv_sigmoid(sum_o1) d_ypred_d_h1=self.w5*deriv_sigmoid(sum_o1) d_ypred_d_h2=self.w6*deriv_sigmoid(sum_o1) #Neuronh1 d_h1_d_w1=x[0]*deriv_sigmoid(sum_h1) d_h1_d_w2=x[1]*deriv_sigmoid(sum_h1) d_h1_d_b1=deriv_sigmoid(sum_h1) #Neuronh2 d_h2_d_w3=x[0]*deriv_sigmoid(sum_h2) d_h2_d_w4=x[1]*deriv_sigmoid(sum_h2) d_h2_d_b2=deriv_sigmoid(sum_h2) #---更新权重和偏差 #Neuronh1 self.w1-=learn_rate*d_L_d_ypred*d_ypred_d_h1*d_h1_d_w1 self.w2-=learn_rate*d_L_d_ypred*d_ypred_d_h1*d_h1_d_w2 self.b1-=learn_rate*d_L_d_ypred*d_ypred_d_h1*d_h1_d_b1 #Neuronh2 self.w3-=learn_rate*d_L_d_ypred*d_ypred_d_h2*d_h2_d_w3 self.w4-=learn_rate*d_L_d_ypred*d_ypred_d_h2*d_h2_d_w4 self.b2-=learn_rate*d_L_d_ypred*d_ypred_d_h2*d_h2_d_b2 #Neurono1 self.w5-=learn_rate*d_L_d_ypred*d_ypred_d_w5 self.w6-=learn_rate*d_L_d_ypred*d_ypred_d_w6 self.b3-=learn_rate*d_L_d_ypred*d_ypred_d_b3 #---在每次epoch结束时计算总损失 ifepoch%10==0: y_preds=np.apply_along_axis(self.feedforward,1,data) loss=mse_loss(all_y_trues,y_preds) print("Epoch%dloss:%.3f"%(epoch,loss)) #定义数据集 data=np.array([ [-2,-1],#Alice [25,6],#Bob [17,4],#Charlie [-15,-6],#Diana ]) all_y_trues=np.array([ 1,#Alice 0,#Bob 0,#Charlie 1,#Diana ]) #训练我们的神经网络! network=OurNeuralNetwork() network.train(data,all_y_trues)
随着网络的学习,损失在稳步下降。
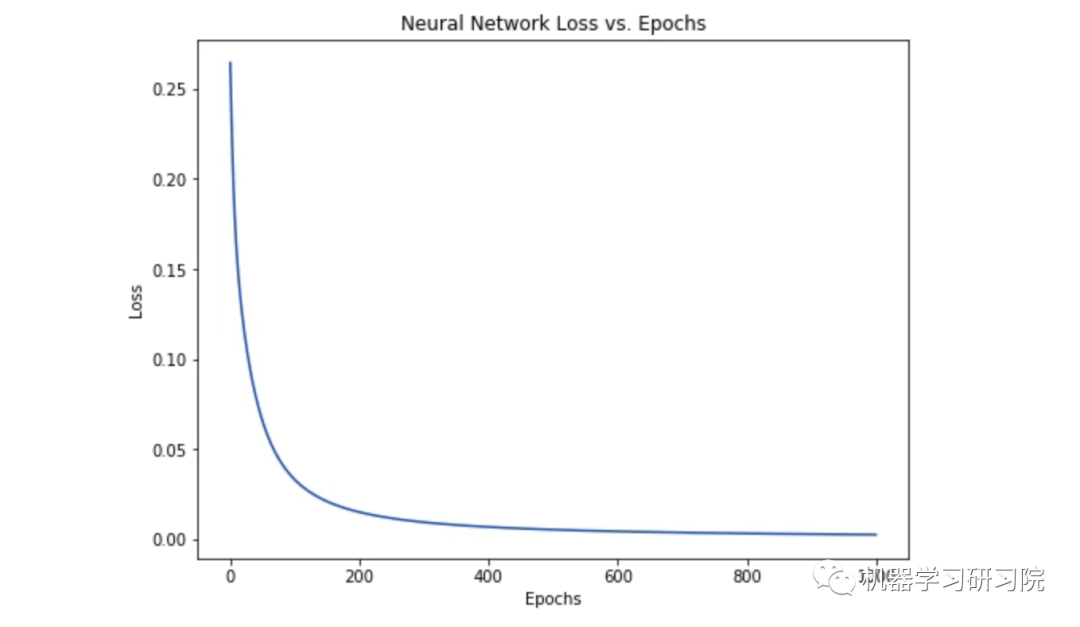
现在我们可以用这个网络来预测性别了:
#做一些预测
emily=np.array([-7,-3])#128磅,63英寸
frank=np.array([20,2])#155磅,68英寸
print("Emily:%.3f"%network.feedforward(emily))#0.951-F
print("Frank:%.3f"%network.feedforward(frank))#0.039-M
接下来?
搞定了一个简单的神经网络,快速回顾一下:
介绍了神经网络的基本结构——神经元;
在神经元中使用S型激活函数;
神经网络就是连接在一起的神经元;
构建了一个数据集,输入(或特征)是体重和身高,输出(或标签)是性别;
学习了损失函数和均方差损失;
训练网络就是最小化其损失;
用反向传播方法计算偏导;
用随机梯度下降法训练网络;
接下来你还可以:
用机器学习库实现更大更好的神经网络,例如TensorFlow、Keras和PyTorch;
其他类型的激活函数;
其他类型的优化器;
学习卷积神经网络,这给计算机视觉领域带来了革命;
学习递归神经网络,常用于自然语言处理;
审核编辑:汤梓红
-
神经网络
+关注
关注
42文章
4789浏览量
101616 -
网络
+关注
关注
14文章
7655浏览量
89649 -
函数
+关注
关注
3文章
4355浏览量
63321 -
神经元
+关注
关注
1文章
368浏览量
18562 -
python
+关注
关注
56文章
4813浏览量
85316
原文标题:从 0 到 1 实现神经网络(Python)
文章出处:【微信号:vision263com,微信公众号:新机器视觉】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
使用Python卷积神经网络(CNN)进行图像识别的基本步骤
labview BP神经网络的实现
【PYNQ-Z2试用体验】神经网络基础知识
人工神经网络实现方法有哪些?
神经网络移植到STM32的方法
用Python从头实现一个神经网络来理解神经网络的原理1
用Python从头实现一个神经网络来理解神经网络的原理2
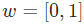
用Python从头实现一个神经网络来理解神经网络的原理3

用Python从头实现一个神经网络来理解神经网络的原理4





 从0到1实现神经网络(Python)
从0到1实现神经网络(Python)










评论