有源滤波器中的低通和高通响应

本文将研究滤波器传递函数本身的相移。虽然滤波器主要针对其幅度响应而设计，但相位响应在延时仿真、级联滤波器级，尤其是过程控制环路等应用中可能很重要。

本文将重点介绍低通和高通响应。本系列的后续文章将研究滤波器的带通和陷波（带抑制）响应、全通响应以及脉冲和阶跃响应。

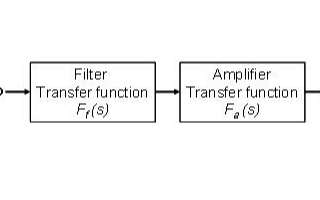
回顾一下，有源滤波器的传递函数可以看作是滤波器传递函数和放大器传递函数的级联响应（图1）。

图1.滤波为两个传递函数的级联。

低通传递方程

首先，我们将重新检查传递方程的相位响应。

对于单极点低通情况，传递函数的相移由下式给出：

(1)

其中 ω 表示弧度频率（ω = 2πf 弧度每秒;1 Hz = 2π 弧度每秒）和 ω0表示滤波器的弧度中心频率。中心频率也可以称为截止频率。就相位而言，中心频率将是相移处于其范围50%的频率。由于弧度频率是用一个比率，频率比，楼/楼0，可方便地替代 ω/ω0.

图2（左轴）评估了公式1从低于中心频率二十倍频到高于中心频率二十倍频的十倍频程。由于单极点低通具有90°的相移范围（从0°到90°），因此中心频率的相移为–45°。在 ω = ω 时0归一化中心频率为 1。

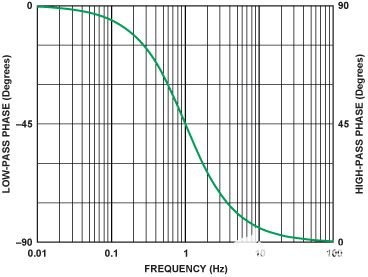
图2.中心频率为1的单极点低通滤波器（左轴）和高通滤波器（右轴）的相位响应。

类似地，单极点高通滤波器的相位响应由下式给出：

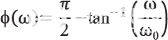(2)

图2（右轴）计算了公式2从低于中心频率二十倍频程到高于中心频率二十倍频程的系数。中心频率（=1）的相移为+45°。

如果低通通带定义为低于截止频率的频率，高通通带定义为高于中心频率的频率，请注意，最低相移（0°至45°）在通带内。相反，最高相移（45°至90°）发生在阻带（高于低通截止频率和低于高通截止频率的频率）。

在低通情况下，滤波器的输出滞后于输入（负相移）;在高通情况下，输出领先于输入（正相移）。图3显示了波形：输入正弦波信号（中心迹线）、1 kHz截止单极点高通滤波器的输出（顶部迹线）和1 kHz截止单极点低通滤波器的输出（底部迹线）。信号频率也是1 kHz，即两个滤波器的截止频率。波形的45°超前和滞后清晰可见。

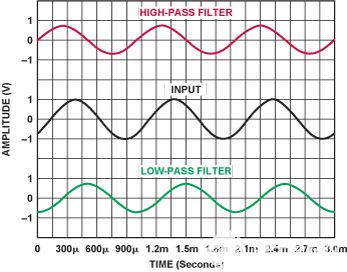
图3.单极点高通滤波器（顶部迹线）和低通滤波器（底部迹线）的输入（中心迹线）和输出。

对于二阶低通情况，传递函数的相移可以近似为：

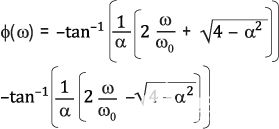
(3)

图4（左轴）从中心频率以下二十倍频到高于中心频率二十倍频的计算（使用α = √2 = 1.414）。这里的中心频率为1，相移为–90°。

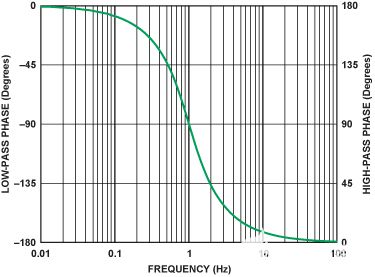
图4.中心频率为2的1极点低通滤波器（左轴）和高通滤波器（右轴）的相位响应。

α，在公式3中，滤波器的阻尼比是Q的倒数（即Q = 1/α）。它决定了幅度（和瞬态）响应的峰值和相变的尖锐度。1.414 的α表征了 2 极巴特沃斯（最大平坦）响应。

2极点高通滤波器的相位响应近似公式为：

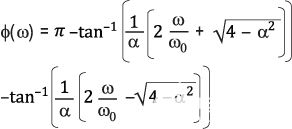
(4)

在图4（右轴）中，该方程用α = 1.414从低于中心频率二十倍频二十倍频到高于中心频率二十倍频的计算。在中心频率（=1）处，相移为90°。

图2和图4使用单曲线，因为高通和低通相位响应相似，只是偏移了90°和180°（π/2和π弧度）。这相当于相位符号的变化，导致低通滤波器的输出滞后，高通滤波器的输出超前。

实际上，高通滤波器实际上是一种宽带带通滤波器，因为放大器的响应至少会引入一个低通极点。

图5显示了2极点低通滤波器的相位和增益响应，绘制为Q的函数。传递函数表明，相变可以分布在相当宽的频率范围内，并且变化的范围与电路的Q成反比。虽然本文主要讨论相位响应，但相位变化率和幅度变化率之间的关系值得考虑。

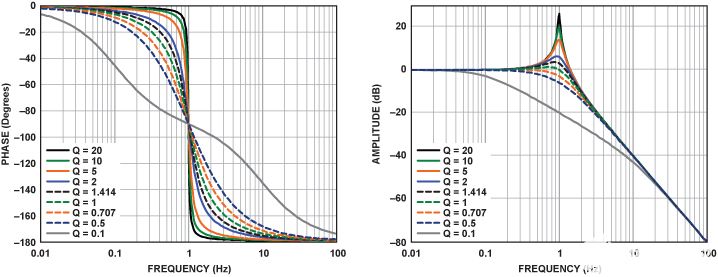
图5.2极点低通滤波器部分的相位和幅度响应与Q的函数关系。

请注意，每个 2 极部分提供最大 180° 的相移;在四肢，–180°的相移虽然滞后了360°，但与180°的相移具有相同性质的角度。出于这个原因，多级滤波器通常会在有限的范围内绘制，例如 180° 到 –180°，以提高读取图形的准确性（见图 9 和图 11）。在这种情况下，必须认识到，绘制的角度实际上是 360° ×正负 m 的真实角度。虽然在这种情况下，图形的顶部和底部似乎存在不连续性（当绘图过渡±180°时），但实际相位角正在平滑而单调地变化。

图6显示了具有不同Q值的2极点高通滤波器的增益和相位响应。传递函数表明，180°的相变可以在较大的频率范围内发生，并且变化的范围与电路的Q成反比。另请注意，曲线的形状非常相似。特别是，相位响应具有相同的形状，只是范围不同。

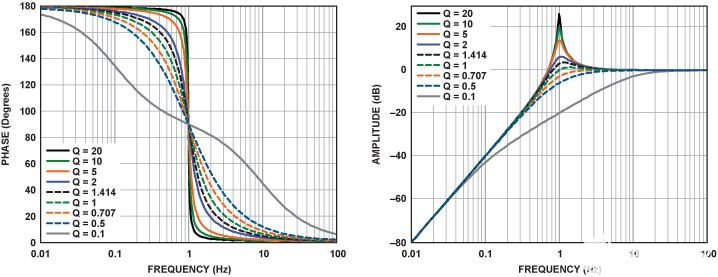
图6.2极点高通滤波器部分的相位和幅度响应与Q的函数关系。

放大器传递函数

放大器的开环传递函数基本上是单极点滤波器的传递函数。如果是反相放大器，它实际上是在插入180°的额外相移。放大器的闭环相移通常被忽略，但如果其带宽不足，它会影响复合滤波器的整体传输。本文选择AD822进行滤波器仿真。它会影响复合滤波器传递函数，但仅限于较高频率，因为它的增益和相移保持在比滤波器本身的转折频率高得多的频率。数据手册中AD822的开环传递函数如图7所示。

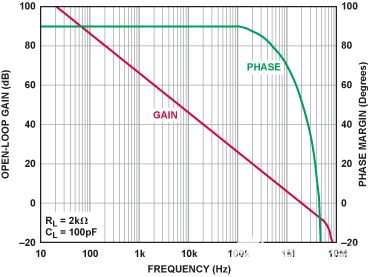
图7.AD822 博德图增益和相位。

示例 1：1kHz、5 极点、0.5 dB 切比雪夫低通滤波器

例如，我们将研究一个1 kHz、5极点、0.5 dB切比雪夫低通滤波器。此特定选择的几个原因：

1）与巴特沃斯的情况不同，各个部分的中心频率都不同。这允许图形将跟踪进一步展开，因此图形更有趣。

2）Q通常更高一些。

3）奇数极强调单极和双极截面之间的差异。

滤波器部分是使用ADI公司网站上的滤波器设计向导设计的。

这f0各节的 和 Q 如下：

f01= 615.8 赫兹	f02= 960.8 赫兹	f03= 342 赫兹
Q1 = 1.178	Q2 = 4.545

图8显示了整个滤波器的原理图。选择的滤波器拓扑——多反馈（MFB）——也是任意的，选择将单极部分作为有源积分器而不是简单的缓冲无源RC电路也是如此。

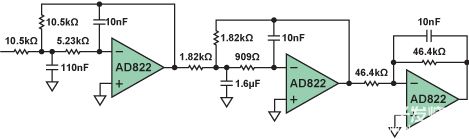
图8.1kHz、5极点、0.5 dB切比雪夫低通滤波器。

图9显示了整个滤波器每级的相移。该图显示了第一部分（第 1 部分 - 蓝色）、前两部分（第 1 部分和第 2 部分 - 红色）和完整滤波器（第 1、2 和 3 部分 - 绿色）的相移。其中包括滤波器部分的基本相移、每个反相放大器贡献的 180° 以及放大器频率响应对整体相移的影响。

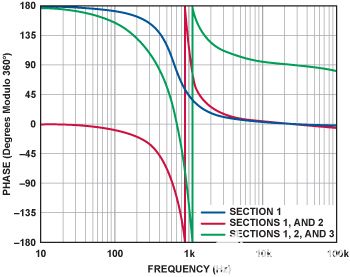
图9.图1中5 kHz、0极点、5.8 dB切比雪夫低通滤波器的相位响应。

一些有趣的细节：首先，相位响应是净滞后，会累积为负数。由于低频时的放大器相位反转，第一个 2 极部分从 –180° （=180° 模 360°） 开始，在高频下增加到 –360° （=0° 模 360°）。第二部分增加了另一个从–540°（=180°模360°）开始的反相，在高频下相位增加到–720°（=0°模360°）。 第三部分在低频下从–900°（= 180°模360°）开始，在高频下增加到–990°（= 90°模360°）。 另请注意，在高于10 kHz的频率下，由于放大器的频率响应，相位会略有滚降。这种滚降被认为是累积的，每个部分都在增加。

示例 2：1kHz、5 极点、0.5 dB 切比雪夫高通滤波器

第二个示例（见图10）考虑了1 kHz、5极点、0.5 dB切比雪夫高通滤波器的相位响应。在这种情况下，滤波器设计（再次使用滤波器设计向导）采用Sallen-Key电压控制电压源（VCVS）部分，而不是多反馈（MFB）。虽然VCVS是一个任意选择，但每个2极部分只需要两个电容器，而不是MFB的每个部分三个电容器，并且前两个部分是同相的。

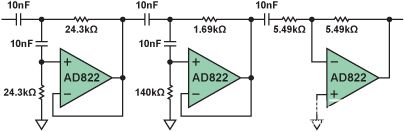
图 10.1kHz、5极点、0.5 dB切比雪夫高通滤波器。

图11显示了滤波器各部分的相位响应。第一部分的相移在低频时从180°开始，在高频下下降到0°。第二部分在低频时增加 180°，从 360°（= 0° 模 360°）开始，在高频时下降到 0°。第三部分增加了相位反转，从低频的–180° + 90° = 90°开始，下降到–540°（= –180°模360°）。再次注意由于放大器频率响应而在高频下的额外滚降。

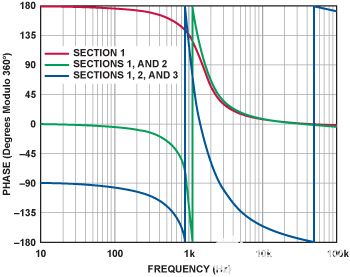
图 11.图1中5 kHz、0极点、5.8 dB切比雪夫低通滤波器的相位响应。

结论

本文考虑低通和高通滤波器的相移。本系列的上一篇文章研究了与滤波器拓扑相关的相移。在以后的文章中，我们将介绍带通、陷波和全通滤波器——在最后一部分中，我们将将它们结合在一起，并研究相移如何影响滤波器的瞬态响应，研究群延迟、脉冲响应和阶跃响应。

审核编辑：郭婷