本章将描述一维卡尔曼滤波器,主要目标是简单直观地解释卡尔曼滤波器的概念,所以,这个过程并不会使用看起来复杂和令人困惑的数学工具,我们将一步一步的向卡尔曼滤波方程靠近。
- 首先,我们通过一个没有过程噪声的简单示例来推导出卡尔曼滤波方程。
- 然后,我们添加过程噪声。
无过程噪声的一维卡尔曼滤波器
正如我前面提到的,卡尔曼滤波器有五个方程,我们已经熟悉了其中两个:
- 状态更新方程。
- 状态推导方程
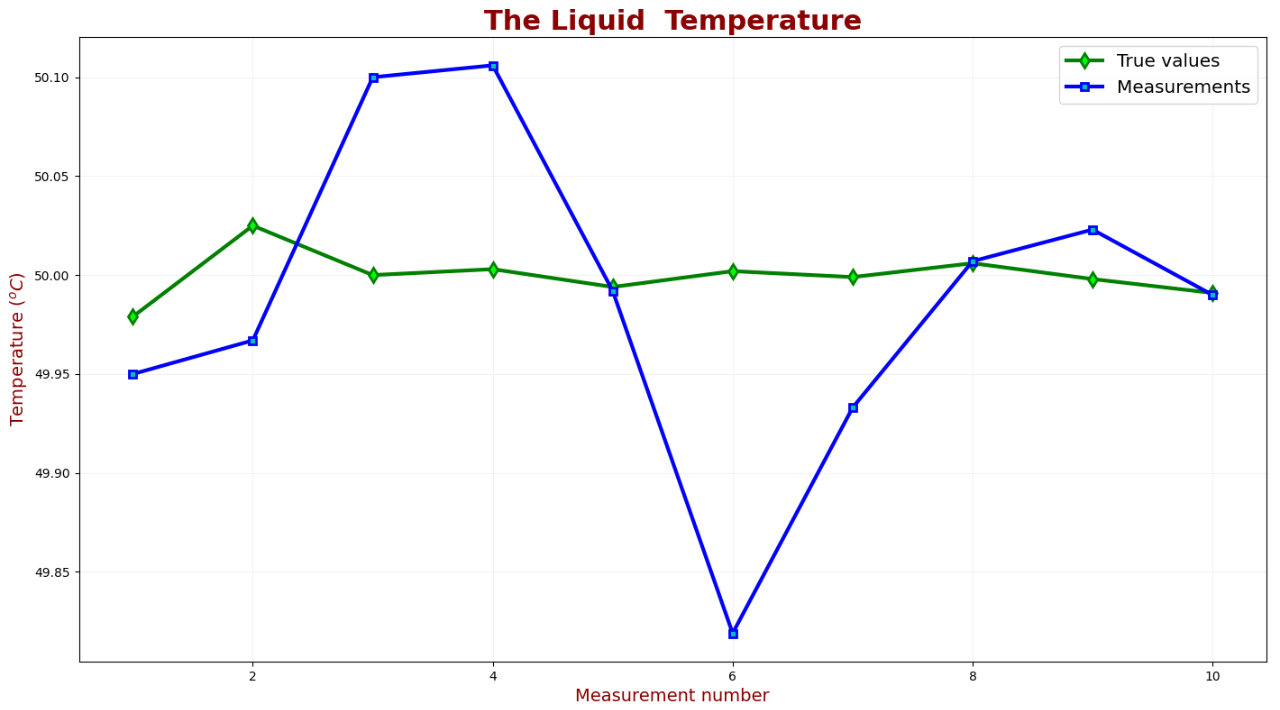
在本章中,我们将导出另外三个卡尔曼滤波方程。让我们回忆一下我们的第一个例子(金条重量测量);我们进行了多次测量,并通过计算平均值作为估计值。我们得到了以下结果:
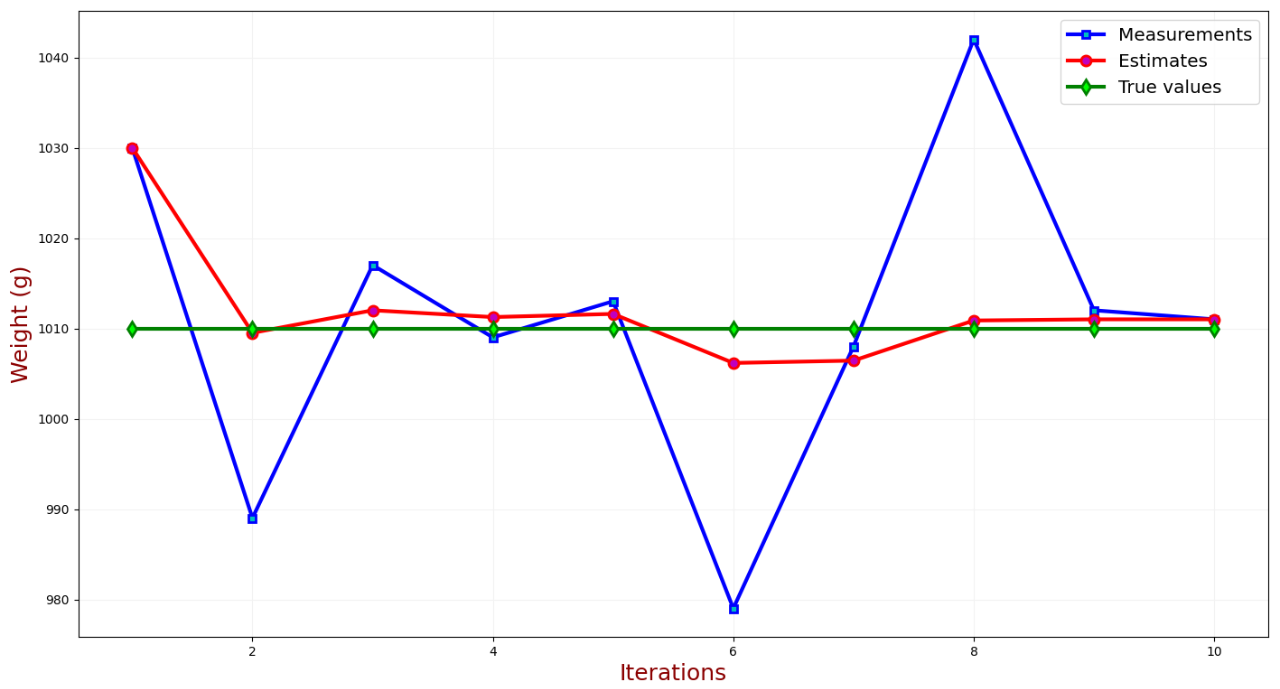
在上图中,可以看到不同迭代过程黄金重量的真实值、估计值以及测量值。测量值(蓝色线)和真实值(绿色线)之间的差异被称为测量误差,由于测量误差是随机的,我们可以用方差(σ2)来描述它。测量误差的方差可由天平供应商提供或通过校准程序得到,测量误差的方差也被称为测量不确定程度。我们用
r
表示测量不确定度。
估计值(红线)和真实值(绿线)之间的差异被称为估计误差,可以看到,当我们进行的测量越多,估计误差变得越来越小,并趋向于0,估计值趋向真实值,虽然我们不知道怎么精确描述估计误差,但我们可以对估计过程中存在的不确定性进行近似估计。我们用
p
表示估计的不确定度。
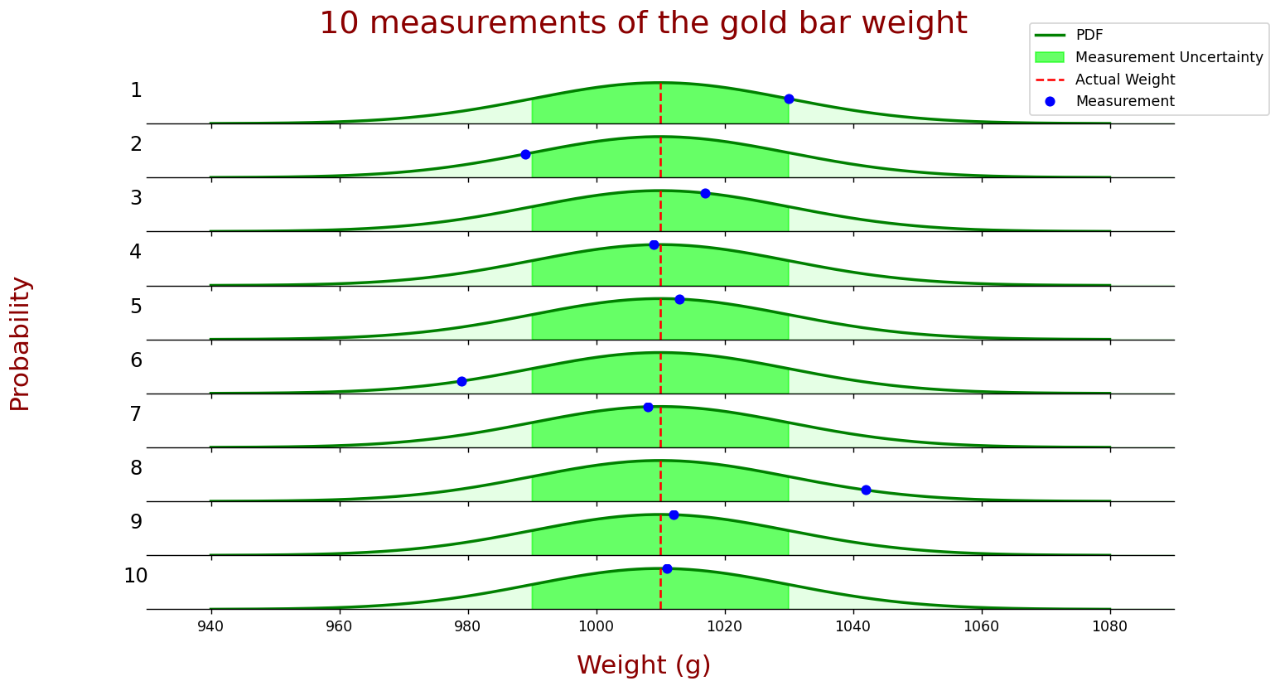
让我们看看重量测量PDF(概率密度函数)。下图显示了金条重量的十个测量值。
- 蓝色圆圈表示测量值。
- 真实值由红色虚线表示。
- 绿线描述了测量的概率密度函数。
- 深绿色区域是测量的标准偏差(σ),即测量值位于该区域内的概率为68.26%
如图所见,10次测量中有8次接近真实值,都位于1σ区域内。测量不确定度(r)就是测量的方差(σ2)。
一维下的卡尔曼增益方程
下面我先直接给出五个卡曼方程中的第三个方程:卡尔曼增益方程,数学推导将在后续章节中给出。卡尔曼增益(由Kn表示)决定当前状态估计值和测量值的权重,与α-β-γ参数不同,卡尔曼增益是每次迭代过程中动态计算的。在一维中,卡尔曼增益方程如下:
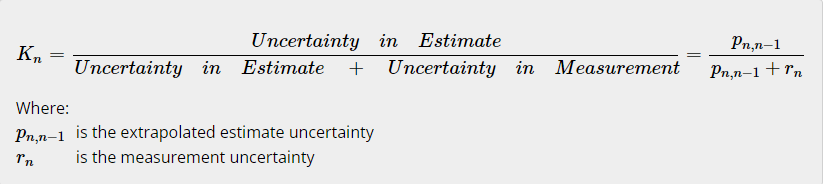
卡尔曼增益是介于0和1之间的数字:
0≤Kn≤1
让我们重写状态更新方程:
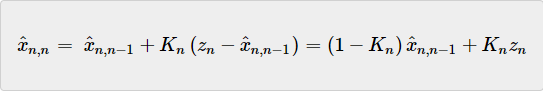
由公式可见,卡尔曼增益(Kn)决定了测量值的权重,(1−Kn)决定了估计值的权重。当测量不确定度非常大且估计不确定度很低时,卡尔曼增益接近于零,说明测量值不太可信,因此,我们对估计值给予很大的权重,对测量值给予较小的权重。相反,当测量不确定度很低且估计不确定度大时,卡尔曼增益接近1,说明估计值不太可信,因此,我们对估计值给予了较低的权重,对测量值给予了较大的权重。如果测量不确定度等于估计不确定度,则卡尔曼增益等于0.5,说明两者可信度一样,最终结果取两者平均。
卡尔曼增益表示测量值对估计值的影响。
卡尔曼增益方程是第三个卡尔曼滤波器方程。
一维下的估计不确定度
更新方程
下式定义了估计不确定度更新方程:

该方程更新了当前状态的估计不确定度,它又被称为协方差更新方程,为什么是协方差?我们将在后续章节中看到这一点。从方程中可以看出,因为(1−Kn)≤1,随着滤波器迭代次数增多,估计的不确定度不断变小,当测量不确定度大时,卡尔曼增益小,因此,估计不确定度的收敛将会很慢,然而,当测量不确定度很小时,卡尔曼增益很高,因此,估计的不确定度将迅速收敛为零。
协方差更新方程是第四个卡尔曼滤波方程。
一维下的估计不确定度
推导方程
与状态推导方程一样,估计不确定度的推导方程也取决于动态系统的类型。在我们的第二个例子中,一维雷达的情形,预测的目标位置是:
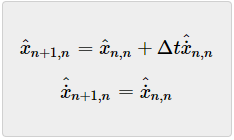
预测位置等于当前估计位置加上当前估计速度乘以时间,预测速度等于当前速度估计值(假设恒定速度模型)。估计不确定度推导方程为:

预测位置的估计不确定度等于当前位置估计不确定度加上当前速度估计不确定度乘以时间平方,预测速度估计不确定度等于当前速度估计不确定度(假设恒定速度模型)。在我们的第一个例子(金条重量测量)中,系统是恒定的,因此,估计不确定度推导方程为:
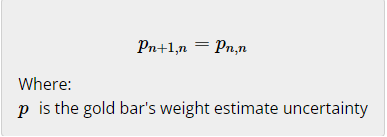
估计不确定度推导方程也被称为协方差推导方程,这是第五个卡尔曼滤波方程。
汇总到一起:
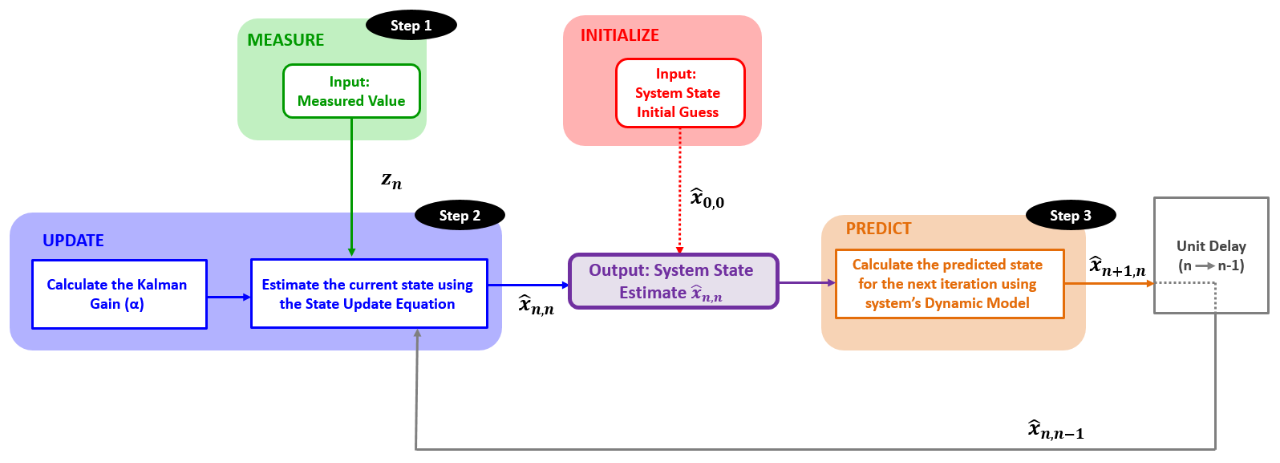
将所有前面提到的碎片组合成一个算法,与α、β、γ滤波器一样,卡尔曼滤波器也使用“测量、更新、预测”算法。下图提供了算法的低级示意图描述:
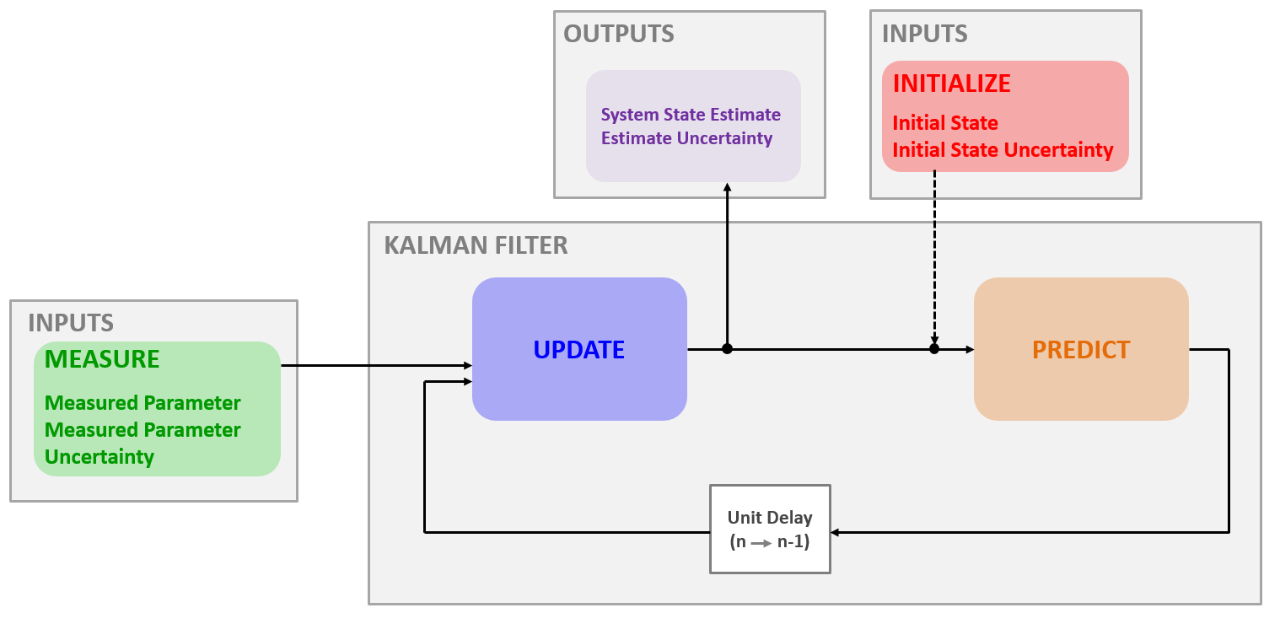
滤波器的输入:
- 初始化
初始化只执行一次,它提供两个参数: 初始系统状态
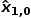
初始状态不确定度(p1,0)初始化参数可以由另一个系统、另一个过程(例如,雷达中的搜索过程)或基于对经验、理论知识的猜测提供,即使初始化参数不精确,卡尔曼滤波器也能够收敛到接近真实值。
- 测量
每个滤波器周期都要进行测量,并提供两个参数:除了测量值之外,卡尔曼滤波器还需要测量不确定度参数,通常,该参数由设备供应商提供,或可通过设备校准得出,雷达测量的不确定度取决于几个参数,如SNR(信噪比)、波束宽度、带宽、目标时间、时钟稳定性等,并且雷达每次测量都有不同的信噪比、波束宽度和目标时间,因此,雷达每次都需要重新计算测量的不确定度,并将其报告给跟踪器。
滤波器输出为:
系统状态估计(
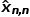
)估计不确定性(pn,n)除了系统状态估计,卡尔曼滤波器还提供了估计不确定度!这个在前面已经提到了,估计不确定度由以下公式给出:
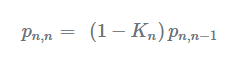
并且pn,n随着滤波器迭代增加不断变小,因为(1−Kn)≤1.因此,可以根据任务要求的精度来决定测量多少次,如果我们正在测量建筑物高度,并且我们要求误差在3厘米(σ)内,我们应该持续进行测量,直到估计不确定度(σ2)小于9。下表总结了五个卡尔曼滤波器方程:
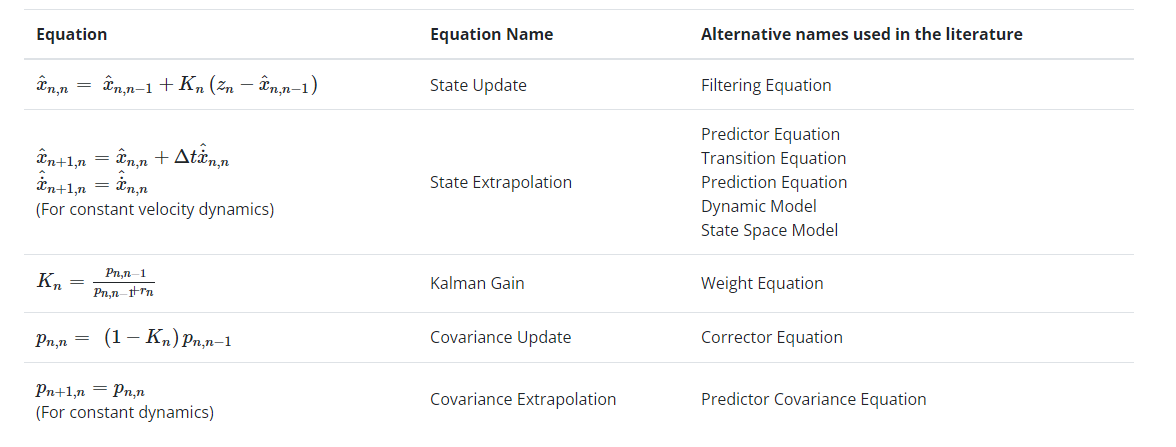
注意1: 状态推导方程和协方差推导方程取决于系统模型。注意2: 上表展示了针对特定情况定制的卡尔曼滤波器方程的特殊形式,方程的一般形式将在后面的矩阵表示法中给出,现在,我们的目标是理解卡尔曼滤波器的概念。
下图提供了对于卡尔曼滤波器框图的详细描述:

步骤0:初始化如上所述,初始化只执行一次,它提供两个参数:初始系统状态(
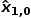
)初始状态不确定性(p1,0)初始化之后是预测。步骤1:测量 测量过程提供两个参数:系统状态测量值(zn)测量不确定度(rn)步骤2:状态更新状态更新过程负责对系统当前状态的估计状态更新过程输入包括:测量值(zn)测量不确定度(rn)前一个系统状态估计(
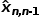
)估计不确定度(pn,n−1 )基于输入,状态更新过程计算卡尔曼增益并提供两个输出:当前系统状态估计(
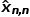
)当前状态估计不确定性(pn,n)这些参数是卡尔曼滤波器输出步骤3:预测预测过程基于动态系统模型,根据当前系统状态和当前系统状态估计不确定度推导得到下一个系统状态,在第一次滤波器迭代时,初始化输出被视为先前状态估计和不确定度,预测输出变成后续滤波器迭代中前一个状态估计和不确定度。
卡尔曼增益直观理解
在计算新的估计时,卡尔曼增益定义了测量的权重和先前估计的权重。
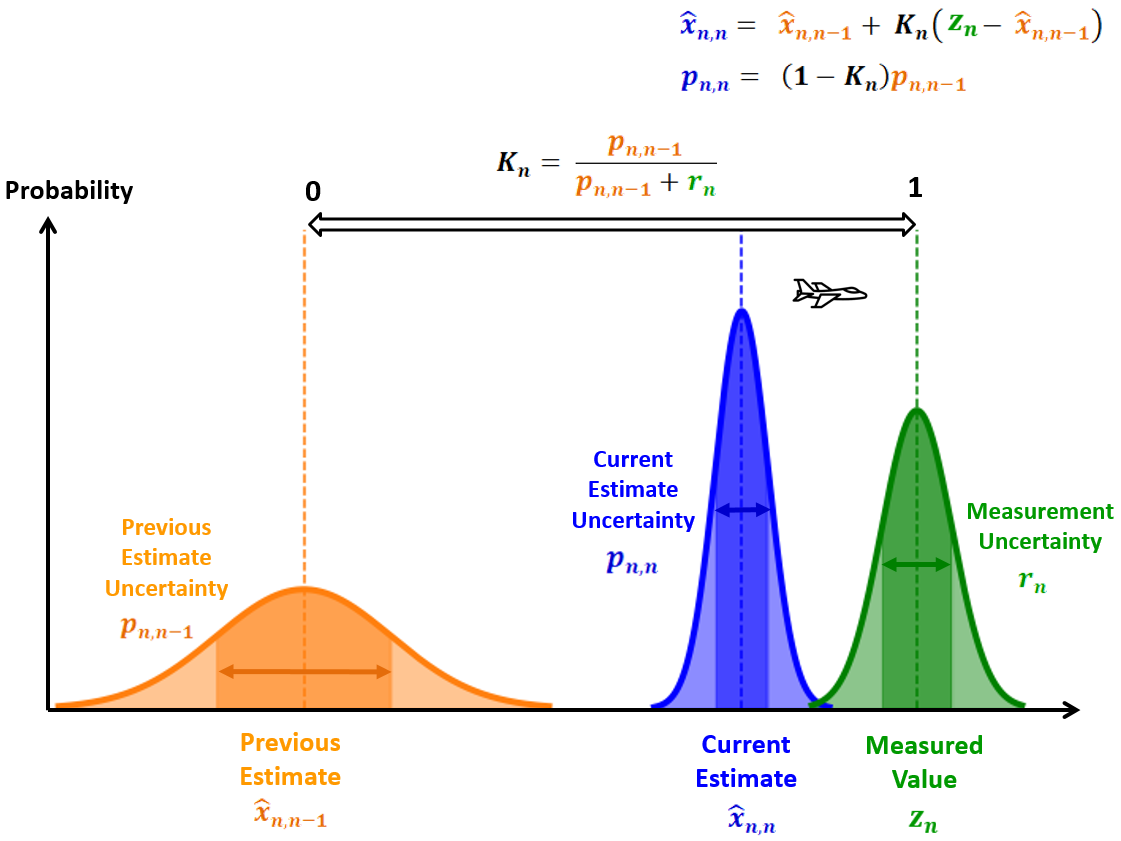
高卡尔曼增益:
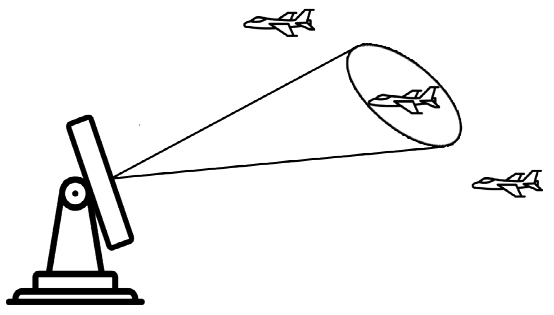
相对于估计不确定度,低测量不确定性将导致高卡尔曼增益(接近1),因此,新的估计值将接近测量值,下图说明了飞机跟踪应用中高卡尔曼增益对估计的影响。
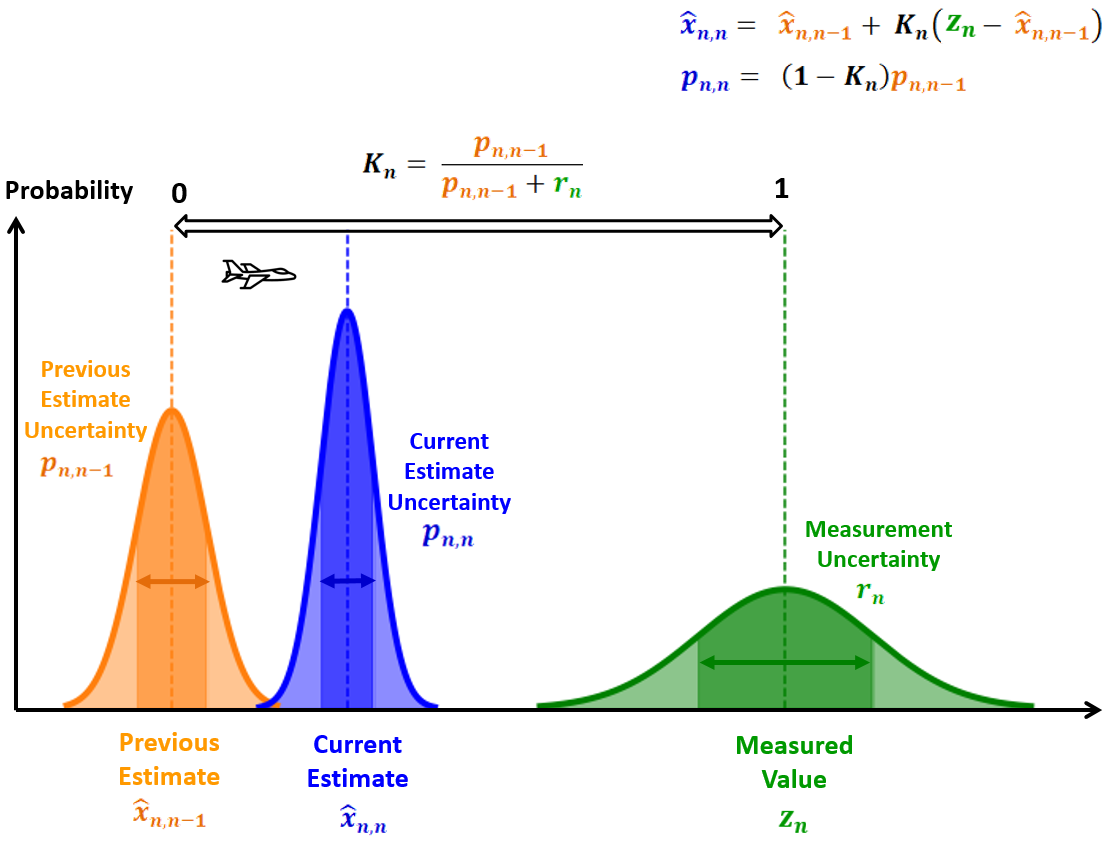
低卡尔曼增益:
相对于估计不确定度,高测量不确定度将导致低卡尔曼增益(接近0),因此,新的估计值将接近先前的估计值,下图说明了低卡尔曼增益对飞机跟踪应用中估计值的影响。
现在我们了解了卡尔曼滤波算法,并准备好了第一个数值示例。
-
滤波器
+关注
关注
162文章
8003浏览量
180382 -
卡尔曼
+关注
关注
0文章
21浏览量
12242
发布评论请先 登录
相关推荐
卡尔曼滤波器的使用原理
卡尔曼滤波器原理
如何理解卡尔曼滤波器?卡尔曼滤波器状态方程及测量方程
卡曼滤波器入门教程概述
卡曼滤波器入门教程数学基础1
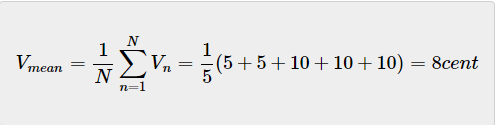





 卡曼滤波器入门教程一维卡曼滤波器 1
卡曼滤波器入门教程一维卡曼滤波器 1
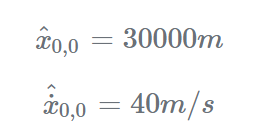

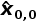










评论