电与电路的基本知识

一、电的基本概念

1、电

电是物质内所含粒子（质子、电子）运动时的一种能量表现形式，实质上是一种能量，常称作电能。

2、电子

电子是最早发现的基本粒子，带负电，电量为1.602×10⁻¹⁹库仑，是电量的最小单元，质量为9.1×10⁻³¹kg，常用符号e表示。

电子和中子、质子组成原子，电子带负电，中子不带电，质子带正电。

3、电荷

带电的基本粒子称为电荷。带正电的粒子叫正电荷，符号为（“+”）；带负电的粒子叫负电荷，符号为（“﹣”）。同种电荷相互排斥，异种电荷相互吸引。

4、电量

带电粒子（质子、电子）所带电荷的多少叫电量。符号Q，单位库仑（C）。

5、电流

单位时间内通过导体任一横截面的电量叫电流。符号I，单位安（A）。电荷在电场力的作用下定向移动形成电流。正电荷定向移动的方向规定为电流方向。

电流分为直流和交流两类：大小和方向不随时间变化的电流为直流（DC）；大小和方向随时间变化的电流为交流（AC）。

6、电位

电位又叫电势，是指单位电荷在静电场中某一点所具有的电势能。符号φ，单位伏(V)。它的大小和电势参考点选择有关。参考点的电位为零，通常把大地作为参考点。

7、电压

电路中任意两点之间的电位差称为电压。符号U，单位伏（V）。电压大小与电位参考点的选择无关。

电场力移动正电荷的方向规定为电压方向。

8、电动势

即电子运动的趋势，能够克服导体电阻对电流的阻力，使电荷在闭合的导体回路中流动的一种作用。符号E，单位伏V。大小等于非静电力把单位正电荷从电源负极经电源内部移到电源正极所做的功。方向规定为从电源负极经电源内部指向电源正极，与电源端电压的方向相反。

9、电阻

导体阻碍电流通过的能力叫电阻。符号R，单位欧（Ω）。电阻和温度及导体的材质有关，同一导体的电阻大小与导体的长度成正比，与导体的截面积大小成反比。

10、电导

导体传导电流的能力叫电导。符号G，单位西（S）。电导和电阻互为倒数。

11、电容

是指给定电压下自由电荷的储存量，符号C，单位法（F）。大小等于极板上储存电量与极板间电压之比。

12、电感

当电流通过线圈后，在线圈中形成感应磁场，感应磁场又会产生感应电流来抵制通过线圈中的电流。这种电流与线圈的相互作用关系称为电抗，也叫电感，符号L，单位亨利（H）。

13、电功

将电能转换成其他形式能量的过程中，电流所做的功叫电功。符号W，单位焦耳J。生活中常用度kwh做单位。电功大小与电压、电流、通电时间成正比，等于三者的乘积。

14、电功率

电流在单位时间内做的功叫做电功率。符号P，单位瓦W。是表示电流做功快慢的物理量，大小等于导体两端电压与通过导体电流的乘积。

15、电路

电流经过的路径称为电路。

电路一般包括四个部分：电源、负载、连接导线与控制设备。

电路有三种状态：通路、开路和短路。

二、直流电路

直流电路根据其结构不同，可分为简单电路和复杂电路。一般认为不能用电阻串、并联关系简化为无分支电路的就是复杂电路，否则就是简单电路。

1、欧姆定律

欧姆定律是分析和计算电路的最基本定律。

1）部分电路欧姆定律

部分电路欧姆定律是研究不包括电源的一段电路中的电流与两端的电压及电阻三者的关系。其内容是：流过导体的电流强度与这段导体两端的电压成正比，与这段导体的电阻成反比。 I=U/R

2）全电路欧姆定律

全电路是指含有电源的闭合电路。如下图所示，虚线框中的E代表电源电动势，r代表电源内电阻。电源内部的电路称为内电路，电源外部的电路称为外电路。

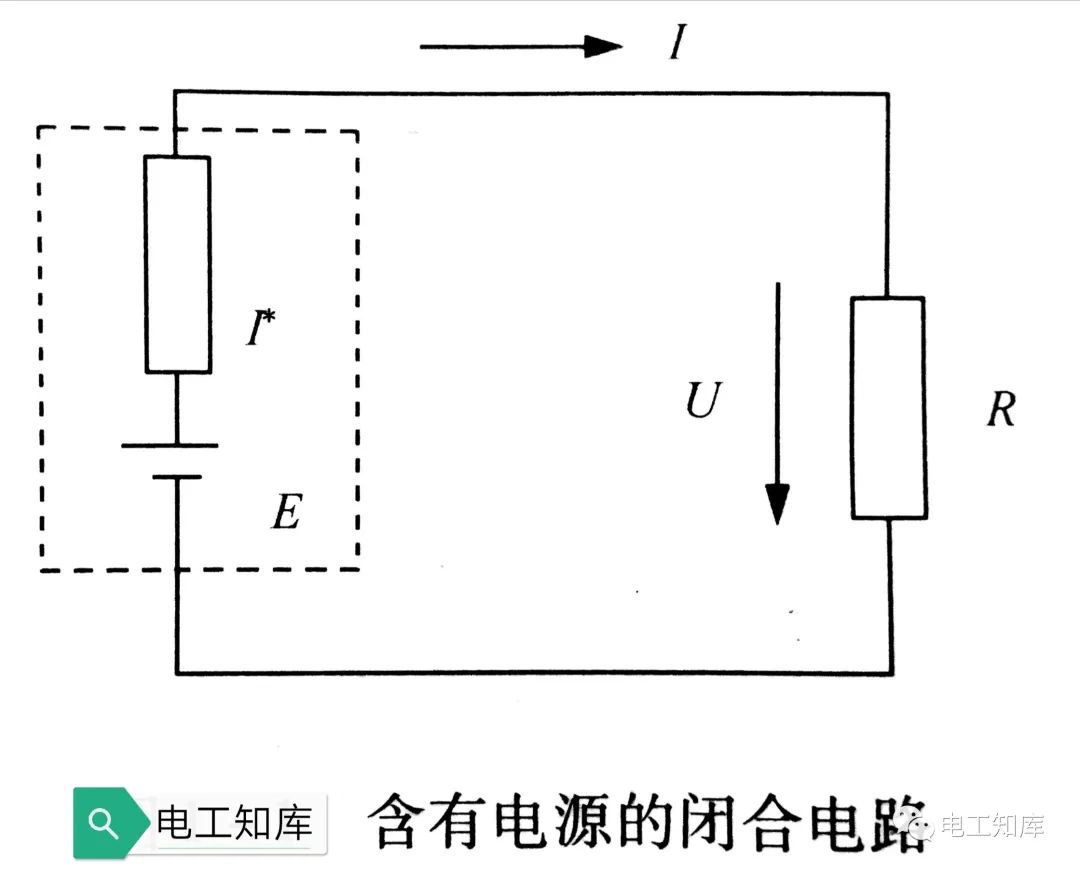全电路欧姆定律的内容是：全电路中的电流强度与电源的电动势成正比，与整个电路的电阻（内电路和外电路）成反比。 I=E/(R+r)

由上式可得 E=ⅠR+Ⅰr=U外+U内

故全电路欧姆定律又可叙述为：电源电动势在数值上等于闭合电路中的各部分电压之和。

外电路电压（U外）是指电路接通时电源两端的电压，又称端电压。

根据全电路欧姆定律分析电路，应有以下三种状态：

（1）通路

合上电路开关，使电源与负载接通，此时的电路称为通路，又叫闭合电路。电路中有电流通过负载，电路处于工作状态即负载状态。

（2）开路

电路的电源断开或保险丝熔断时，电路就处于开路状态即空载状态。此时外电路电阻无穷大，电路中没有电流，电源的端电压等于电动势，电源不输出电能，电路不工作。

I=0 U内=0 U外=E

（3）短路

短路是指电路中不同电位的两点直接接通，即电源未经过负载而直接由导体接通的现象，接通处的电阻极低，一般可视为零，短路状态可能发生在电路的任何地方，但最严重的是电源短路。

U外=0 U内=E

2、基尔霍夫定律

基尔霍夫定律是复杂电路分析计算的基本定律。下图所示是一个比较复杂的直流电路，虽然它的结构看起来简单，元件数很少，但由于R₁、R₂、R₃之间既不是串联关系，也不是并联关系，无法用串、并联进行简化。

对于复杂直流电路，直接用欧姆定律求解是不可能的，复杂电路的计算需用基尔霍夫定律。

1）复杂电路常用术语

（1）支路

由一个或几个元件串联组成的无分支电路称为支路。同一支路中各元件上流过的电流相等。上图中R₁和E₁构成一条支路，R₃单独构成一条支路。

（2）节点

三条或三条以上的支路的交汇点称为节点。如上图中的A点和B点。

（3）回路

电路中任一闭合路径称为回路。如上图中A-R₁-E₁-B-R₃-A构成一个回路。

（4）网孔

不能再分的最简单的回路称为网孔。如上图中A-R₁-E₁-B-R₃-A构成最简单不能再分的一个回路，称为网孔。

2）基尔霍夫第一定律（KCL定律）

又称节点电流定律。基尔霍夫第一定律是关于节点电流的，其内容是：电路中流进任一节点的电流之和恒等于流出该节点的电流之和。又可叙述为：电路中任一节点处电流的代数和恒为零。

基尔霍夫第一定律表明电路中电流的连续性，电荷在任一节点上既不能积累也不能消失。

3）基尔霍夫第二定律（KVL定律）

又称回路电压定律。基尔霍夫第二定律是关于回路电压的，其内容是：任一回路中电动势的代数和恒等于各电阻上的电压降的代数和。如下图：

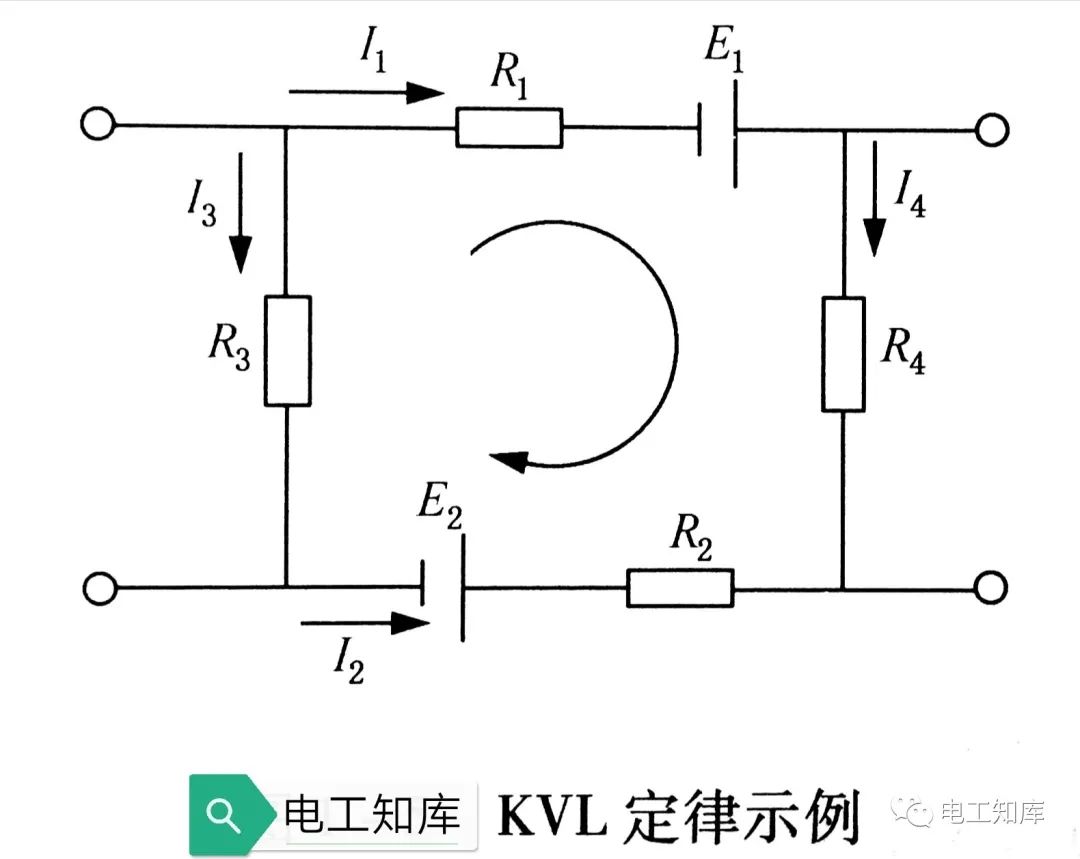E₁- E₂=I₁R₁- I₂R₂ - I₃R₃ + I₄R₄

上式可写成：

I₁R₁- I₂R₂ - I₃R₃ + I₄R₄ - E₁ + E₂=0

故基尔霍夫第二定律又可叙述为：任一回路中各元件上的电压降之代数和恒为零。

基尔霍夫第二定律对不完全由实际元件构成的假想回路仍然适用，如下图：

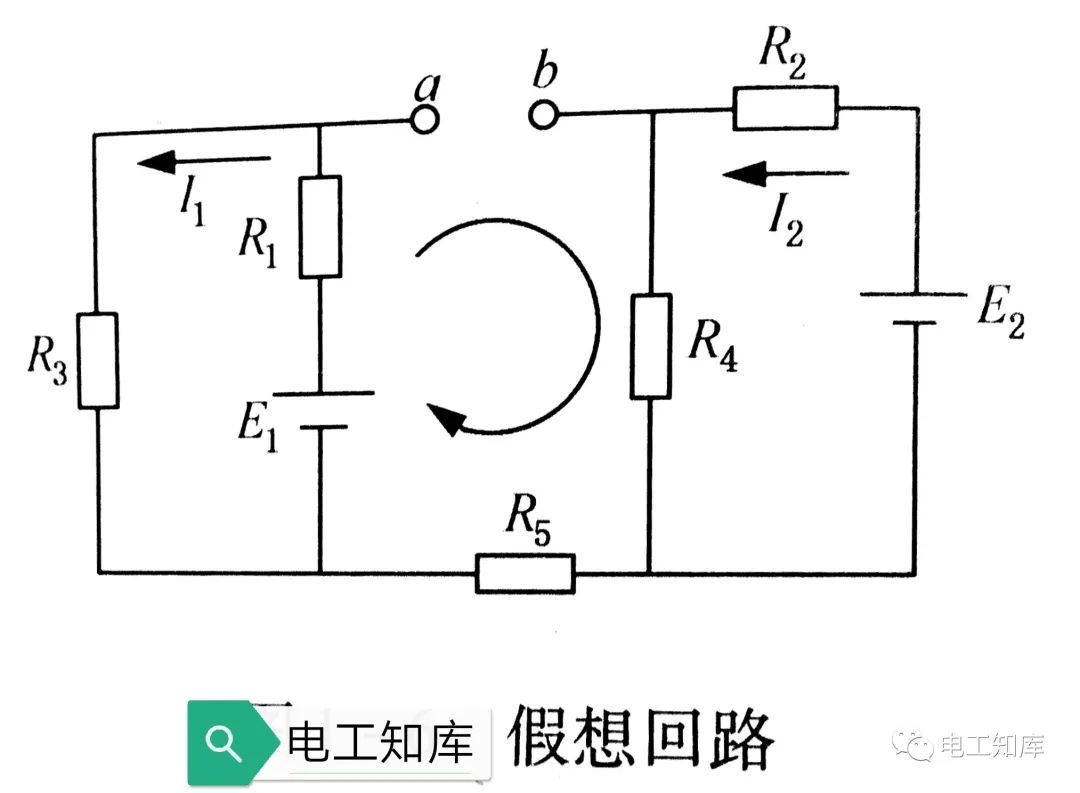Uab + I₂R₄ - E₁ + I₁R₁=0

3、支路电流法

支路电流法是求解复杂电路最基本的方法。解题思路是：以各支路电流为未知量，根据基尔霍夫定律，列出节点电流方程、回路电压方程，解方程组得到各支路电流。一般步骤如下：

1）假设各支路电流参考方向和选定回路绕行方向；

2）根据基尔霍夫第一定律列出独立的节点电流方程；

3）根据基尔霍夫第二定律列出独立的回路电压方程；

4）联合独立的节点电流方程和独立的回路电压方程，然后代入数据解方程组。

4、戴维南定理

比较复杂的电路称为网络，若电路具有两个输出端，则称为二端网络。网络内有电源的称为有源二端网。如下图：

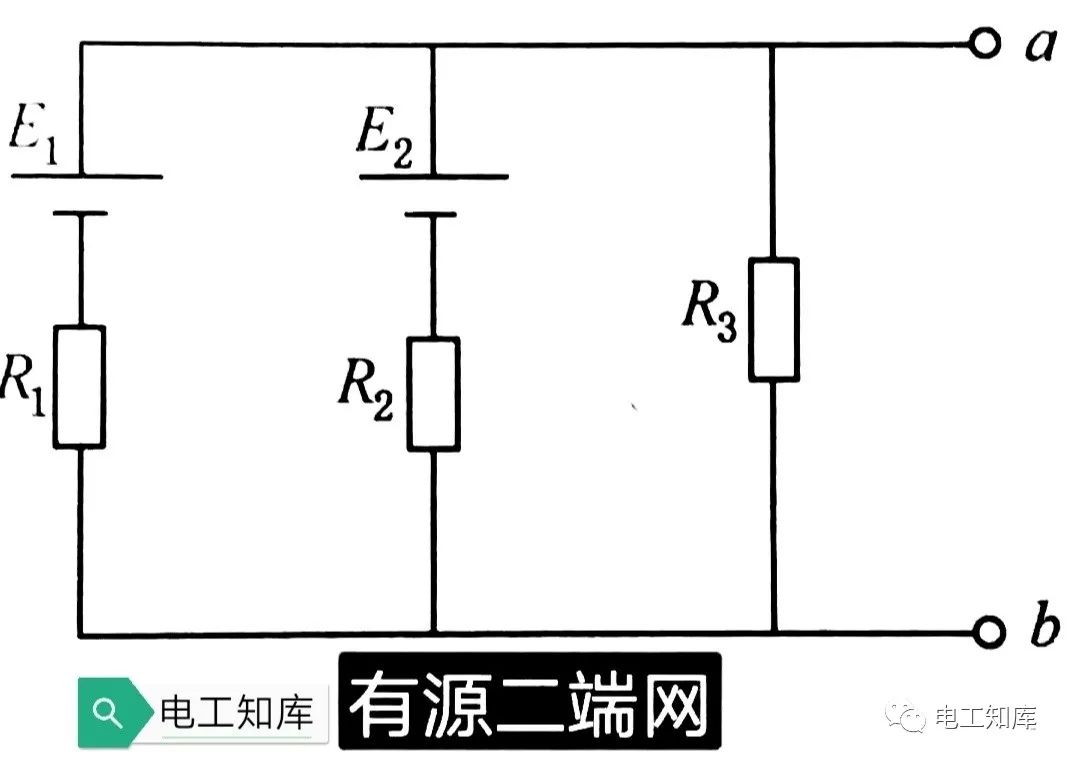不含电源的称为无源二端网。如下图：

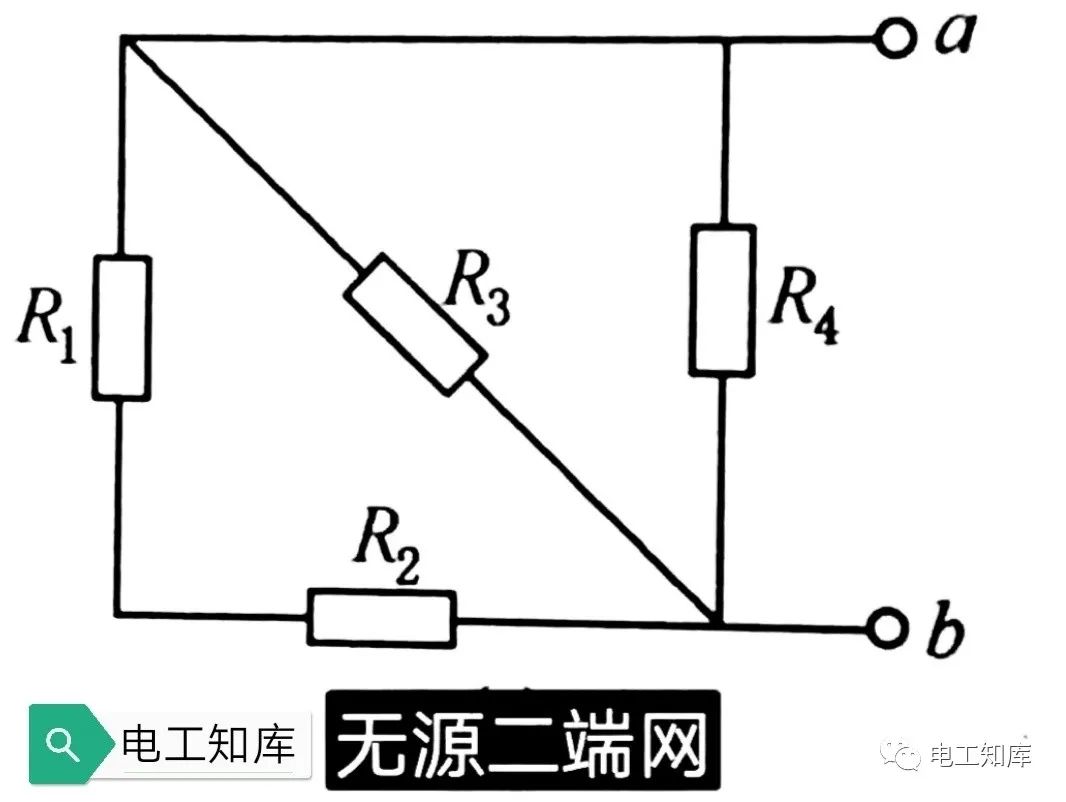有源二端网络相当于一个电源，可以简化为一个具有电动势E₀和电阻Rⅰ的等效电源。如下图所示：

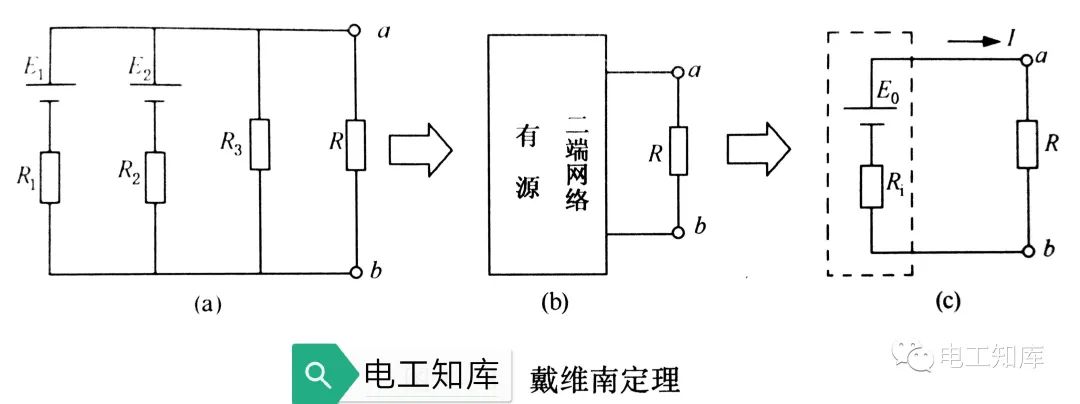戴维南定理指出：任何一个线性有源二端网络对外电路来说，都可以用一个具有电动势E₀和内电阻Ri的等效电源等值替代。电动势E₀的值就等于有源二端网络两点间的开路电压，内阻Ri的值就等于网络内所有电源均不起作用时无源二端网络的等效电阻。

1）用戴维南定理求解某一支路电流的一般步骤如下：

（1）将原电路划分为待求支路和有源二端网络两部分；

（2）断开待求支路，求出有源二端网络的开路电压；

（3）将网络中的各电动势短路，内电阻保留，求出无源二端网络的等效电阻；

（4）画出等效电源，接入待求支路，根据全电路欧姆定律，求出该支路的电流。

2）运用戴维南定理需要注意以下几点：

（1）戴维南定理只适用于线性电路；

（2）根据戴维南定理求出的等效电源只是对外电路等效；

（3）将有源二端网络化为无源二端网络时，网络内的电动势短路，但内阻不能短路；

（4）画等效电源时，电动势的方向必须根据开路电压的正负来确定。

三、正弦交流电路

1、基本概念

1）正弦交流电

按正弦规律变化的交流电称为正弦交流电。正弦交流电任一时刻的值称为正弦交流电的瞬时值，分别用小写字母i、u 、e表示电流、电压、电动势。

2）正弦交流电的三要素

正弦交流电的三要素是最大值、频率、初相角。

（1）最大值

最大值指正弦交流电在一个周期内出现的最大瞬时值的绝对值，分别用Ⅰm、Um、Em表示电流、电压、电动势。

（2）频率

频率是指交流电在1秒中内变化的次数，用f表示，单位为赫兹（Hz），简称赫。

正弦交流电在1秒内所变化的电角度称为角频率，用ω表示，单位为弧度/秒（rad/s）。

交流电每变化一次，所经历的时间为周期，用T表示，单位为秒（S）。交流电每变化一次，电角度变化2π弧度，所以有ω=2πf=2π/T。

（3）初相角

发电机的转子线圈平面开始计时（t=0）时与磁中性面夹角为 α，发电机运行时线圈平面与磁中性面的夹角连续变化。设发电机旋转角速度为ω，则在任一时刻t，线圈与磁中性面的夹角为（ωt+α），所以t时刻线圈中的感应电动势为 e=EmSin（ωt+α） 式中（ωt+α）称交流电的相位角。t=0时的相位角叫初相角。e的初相角是α。

相位差是两个同频率的正弦交流电的初相角之差。

3）正弦交流电的有效值

一个交流电流i和一个直流电流I分别流过完全相同的电阻R，如果在交流电一周期内它们在各自电阻上所产生的热量相等，则交流电流i的有效值就等于直流电流I的大小。正弦交流电有效值与最大值的关系为：I=1/√2Im U=1/√2Um

2、表示方法

1）解析法

用三角函数表示正弦交流电的方法称为解析法。

2）图形法（曲线法）

在直角坐标系中，用横坐标表示时间或电角度，纵坐标表示交流电的瞬时值，根据解析式做出的曲线称为交流电的波形图，如下图：

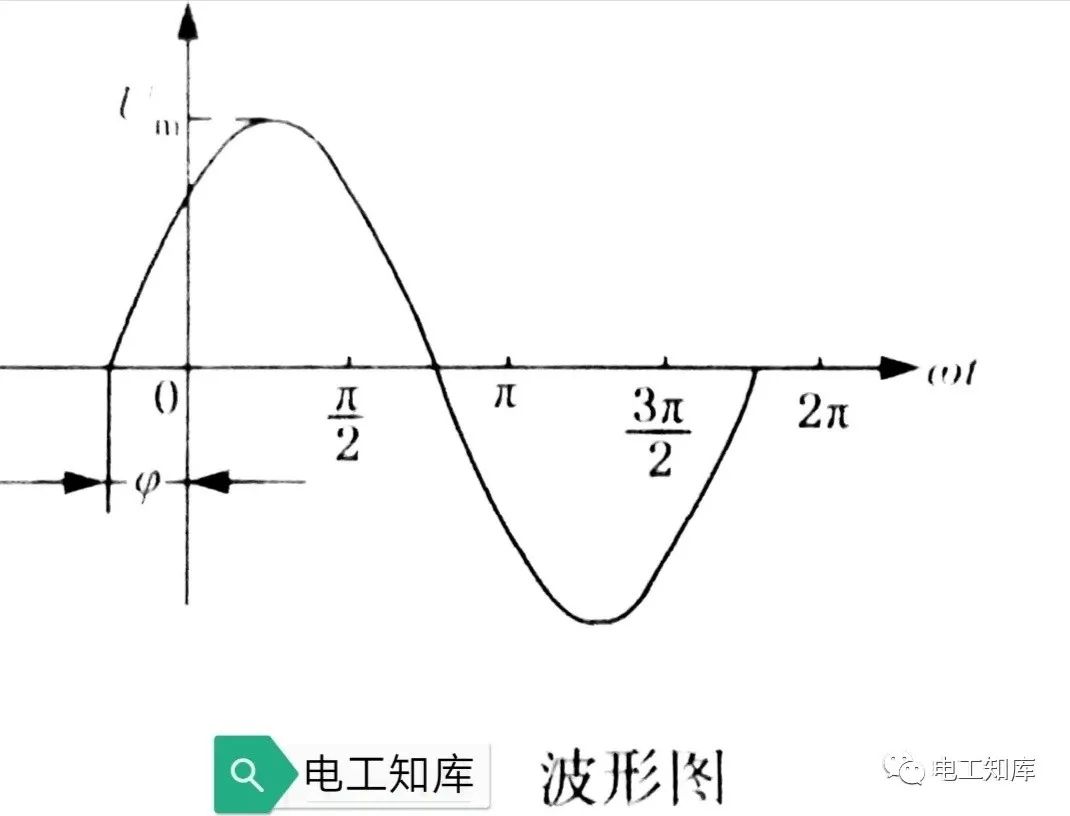用波形图来表示交流电的方法称为图形法。图形法可直观地表示出正弦交流电最大值及初相角的大小，角频率可通过运算求得。

3）旋转矢量法

可以简化正弦交流电的一般加减运算。如下图所示：

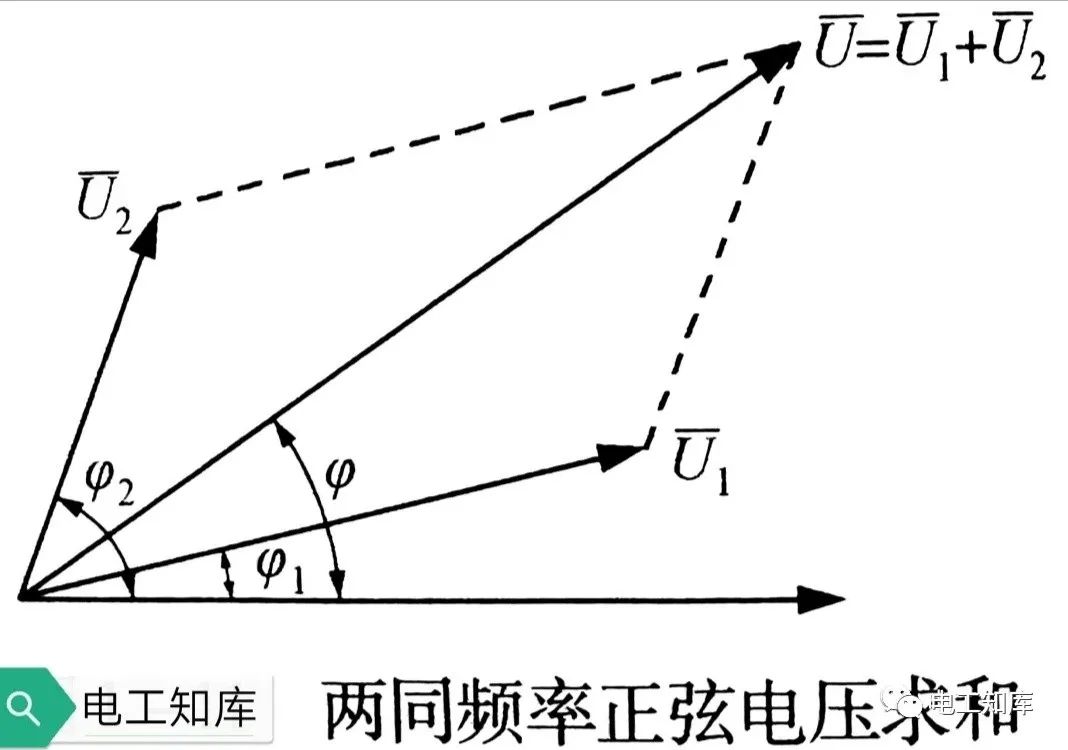两同频率正弦量的求和转化为两旋转矢量的求和，可用平行四边形法则。

4）相量法

正弦量可以用复数来表示，用复数表示正弦量的方法称为相量法。

四、对称三相交流电路

1、对称三相电路的有关概念

1）对称三相电源

三个频率相同，最大值相等，相位互差120°的正弦交流电动势称为对称三相电源 。

2）对称三相负载

对称三相负载是指三相负载的大小相等，性质相同，即负载的复阻抗相等。

3）相序

三相电源中各相电动势（或电压、电流）到达零值（或最大值）的顺序叫做相序。相序有正序、负序和零序三种。

4）对称三相电路

对称三相电源和对称三相负载组成的三相电路称为对称三相电路。

2、对称三相电路的特点

1）相电压与线电压的关系

（1）相电压

相线与零线间的电压称为相电压。用Uu、Uv、Uw表示。

（2）线电压

相线与相线间的电压称为线电压。用Uuv、Uvw、Uwu表示。

（3）负载丫连接时，线电压为相电压的√3倍，且线电压超前相应的相电压30°。

2）相电流与线电流的关系

（1）相电流

各相电源或负载中流过的电流称为相电流。

（2）线电流

相线中流过的电流称为线电流。

（3）负载△连接时，线电流为相电流的√3倍，且线电流滞后相应的相电流30°。

3）三相对称电路的功率

负载丫连接时，U相=U线/√3 I相=Ⅰ线

负载△连接时，U相=U线 l相=Ⅰ线/√3

故不论三相负载作何种连接都有

P=3U相Ⅰ相cosφ=√3U线I线cosφ

Q=3U相Ⅰ相 sinφ=√3U线I线 sinφ

S=3U相I相=√3U线I线

五、电阻串、并联及混联电路

1、电阻串联电路

1）电阻的串联

两个或两个以上的电阻按顺序一个接一个连成一串，使电流只有一条通路的连接方式，称为电阻的串联。

2）电阻串联电路特点

（1）串联电路中各处电流都相等；

（2）串联电路两端的总电压等于各电阻端电压之和；

（3）串联电路的等效电阻等于各串联电阻阻值之和；

（4）串联电路中各个电阻阻值相等时，等效电阻为单个电阻的n倍；

（5）串联电路中各电阻上的电压分配与其阻值成正比，即Ui=Ri/R*U，此式称为分压公式，Ri/R称为分压比；

（6）串联电路的总功率等于各串联电阻所消耗的功率之和；

（7）串联电路中各电阻所消耗的功率与其阻值成正比。

2、电阻并联电路

1）电阻的并联

两个或两个以上的电阻一端连在一起，另一端也连在一起，使每一电阻两端都承受相同的电压，电阻的这种连接方式叫做并联。

2）电阻并联电路特点

（1）并联电路中各支路两端的电压相等，并且等于电路两端的电压；

（2）并联电路中的总电流等于各支路电流之和；

（3）并联电路等效电阻的倒数等于各并联电阻的倒数之和；

（4）并联电路中各个电阻阻值相等时，等效电阻为单个电阻的1/n；

（5）并联电路中任一支路的电流与该支路的电阻值成反比，即Ii=R/Ri*l，此式称为分流公式，R/Ri称为分流比；

（6）并联电路的总功率等于各并联电路所消耗的功率之和；

（7）并联电路中各电阻所消耗的功率与其阻值成反比。

3、电阻混联电路

1）电阻的混联

电路中既有电阻的串联，又有电阻的并联，这种连接方式叫做电阻的混联。

2）混联电路计算步骤

（1）把串联的电阻和并联的电阻分别用等效电阻代替，逐步简化电路，最终求出电路中的等效电阻。

（2）由总等效电阻和电路的端电压计算电路的总电流。

（3）根据电阻串联的分压关系和电阻并联的分流关系，求出各电阻上的电压、电流及功率。

3）等电位法化简混联电路

（1）确定等电位点，标出相应的符号

导线的电阻和理想电流表的电阻可忽略不计，可以认为导线和电流表联接的两点是等电位点。对等电位点标出相应的符号，如a点的等电位点用a′标示。

（2）画出串、并联关系清晰的等效电路图

由等电位点先确定电阻的连接关系，再画出电路图。先画电阻最少的支路，再画次少的支路，从电路的一端画到另一端。

（3）求解

根据欧姆定律，电阻串联、并联的特点和电功率的计算公式列出方程求解。

六、电阻、电感与电容电路

电阻、电感与电容是交流电的三个基本参数。当这些参数是不随电压、电流的大小和时间而改变的常量时，这一电路为线性电路。

1、纯电阻电路

1）在交流电路中，凡由电阻作为负载，如白炽灯、电炉、电烙铁等组成的电路都叫纯电阻电路。

2）纯电阻电路的电压和电流相位相同，电压、电流和电阻之间的关系符合欧姆定律。

3）交流电通过电阻时，总是从电源吸收电能转换成热能，电阻从电源吸收的能量用来做功而消耗掉。交流电通过电阻电路时的平均功率又称有功功率。P=UI=I²R=U²/R

2、纯电感电路

1）在纯电感电路中，由于交流电的大小和方向在不断地变化，因此在电感线圈中会产生自感电动势阻碍电流的变化，这种由电感对交流电产生的阻碍作用叫做感抗。用XL表示，单位为Ω，感抗的大小与通过它的电流频率成正比。XL=ωL=2πfL。在直流路中，由于电流不变化，所以感抗为零，相当于短路。

2）交流纯电感电路中，电压瞬时值超前电流瞬时值90°，电压、电流和感抗之间的关系符合欧姆定律。

3）电感线圈中不消耗有功功率，电源与电感线圈之间不断进行能量交换，这部分功率称为无功功率，单位是var。

3、纯电容电路

1）Xc=1/ωC=1/2πfC，Xc叫容抗，单位为Ω，在直流情况下f=0 ，Xc为无穷大，说明电容有隔直流通交流，阻低频通高频的特性。

2）交流纯电容电路中，电流瞬时值超前电压瞬时值90°，电压、电流和容抗之间的关系符合欧姆定律。

3）纯电容电路中不消耗有功功率，电源与电容之间不断进行能量交换，这部分功率为无功功率，单位是var。

4、R、L、C串联电路

1）阻抗

感抗XL=ωL=2πfL

容抗Xc=1/ωc=1/2πfC

电抗X=XL+Xc

总阻抗Z=√R²＋X²

2）R、L、C分电压

电阻上电压U=IR，U与I同相。

电感上电压U=IXL，U超前电流90°。

电容上电压U=IXc，U滞后电流90°。

3）总电压、总电流关系

总电压与总电流有效值关系符合欧姆定律，I=U/Z。

XL=Xc时，电路呈纯阻性，电压与电流同相位。

XL＞Xc时，电路呈感性，电压超前电流。

XL＜Xc时，电路呈容性，电压滞后电流。

七、功率和功率因数

1、功率

1）电功率

电流在单位时间内所做的功叫做电功率。它是表示电流做功快慢的物理量，用P表示，它的单位是瓦特（Watt），简称"瓦"，符号是W。电功率等于导体两端电压与通过导体电流的乘积。

2）有功功率

在交流电路中，消耗在电阻元件上、不可逆转换的那部分功率（如转变为热能、光能或机械能）称为有功功率，简称“有功”，用“P”表示，单位是瓦（W）或千瓦（KW）。它是交流电在一个周期内瞬时功率的平均值，故又称平均功率。大小等于电阻元件两端电压有效值与通过电阻元件中电流有效值的乘积。

3）无功功率

在交流电路中，电感性或电容性的元件，通电后便会建立起电感线圈的磁场或电容器极板间的电场。在交流电每个周期内的上半部分（瞬时功率为正值）时间内，它们将会从电源吸收能量以建立磁场或电场，而下半部分（瞬时功率为负值）的时间内，其建立的磁场或电场能量又返回电源。即电源的能量与磁场能量或电场能量进行着可逆的能量转换，并不消耗功率。将电感或电容元件与交流电源往复交换的功率称为无功功率，简称“无功”，用“Q”表示。单位是乏（Var）或千乏(KVar)。

4）视在功率

交流电源所能提供的总功率，称为视在功率，在数值上是交流电路中电压与电流的乘积。视在功率用S表示。单位为伏安（VA）或千伏安（KVA）。它通常用来表示交流电源设备（如变压器）的容量大小。它包括有功功率和无功功率。

2、功率因数

1）功率因数的概念

在交流电路中，电压与电流之间的相位差(Φ)的余弦叫做功率因数，用符号cosΦ表示，在数值上，功率因数是有功功率和视在功率的比值，即cosΦ=P/S。有功功率和视在功率的比叫功率因数。它是衡量电气设备效率高低的一个系数。

2）电气设备功率因数低的原因

功率因数低的原因是常用电气设备是电感性的负载，除白炽灯、电阻、电热器等功率因数接近于1外，其他如交流电动机、变压器，电抗器、架空线路及电气仪表的功率因数都小于1。生产中最常见的交流异步电动机在空载时的功率因数只有0.20.3，轻载时约为0.5左右，额定负载时约为0.70.9。其它设备如工频炉、电焊变压器以及日光灯等，负载的功率因数也都较低。这样供电设备的容量不能得到充分利用，例如容量为1000kVA的变压器，如果cosΦ =1,即能送出1000kW的有功功率；而在cosΦ =0.7时，则只能送出700kW的有功功率。

3）提高功率因数的意义

（1）可以提高发电机、变压器等用电设备有功功率的输出，从而提高设备利用率，降低成本。

（2）可以减少电力系统的电能损耗，改善供电质量。

（3）可以减少电力线路的电压损失，满足末端用户电压要求。

（4）通过各元件损失的减少及功率因数提高的电费优惠减少用户的电费支出。

4）提高功率因数的方法

（1）提高自然功率因数，包括合理选择电气设备，避免变压器轻载运行，合理安排工艺流程。

（2）通过人工补偿提高功率因数，最常用的是并联补偿电容器。

（3）条件允许时，尽量采用同步电动机和同步调相机。