4、几何非线性matlab代码实现
(1)非线性求解算法流程总结
在前面的部分中,描述了通过增量迭代数值方法求解线性化平衡方程组的过程。通用求解算法的流程图如图19所示。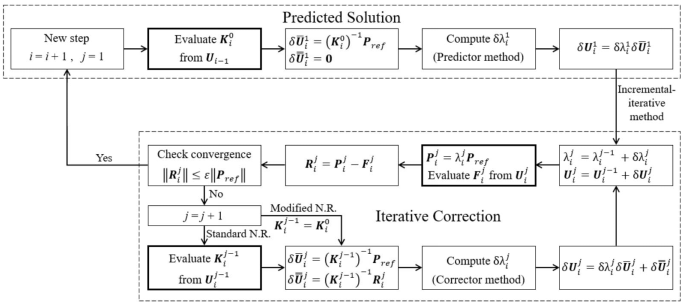
图19
(2)matlab代码实现
① 切线刚度矩阵的matlab代码
根据公式(24),切线刚度矩阵中的弹性刚度矩阵实现代码如下:
根据公式(25),切线刚度矩阵中的几何刚度矩阵实现代码如下,注释掉的部分为应变张量的高阶项,可根据需要决定计算与否:
在上述弹性刚度矩阵和几何刚度矩阵得到后,单元的切线刚度矩阵实现代码为:
② 非线性系统求解的matlab代码
主函数首先初始化节点位移向量 U、载荷比值 lr。然后,增量迭代过程以一个while循环开始,该循环一直运行直到达到最大步数。增量步数计数器在增量循环开始时立即递增。预测阶段从更新UL公式的参考构型开始。
在当前的平衡构型下,即在上一步结束时获得的单元内力和节点位移基础上,计算预测阶段的切线刚度矩阵 Kt。因此,tangStiffMtxUL()函数接收单元结构体数据的向量和节点位移的向量,两者都使用上一步的结果进行了更新。然后,切线刚度矩阵用于计算位移的切线增量d_Ut,通过使用参考载荷矢量求解线性系统,求解线性系统函数solveLinearSystem()。
下一步是计算预测阶段荷载比增量。当增量步是第一步时,预测增量的初始符号s设置为正数,且负载率增量 d_lr认为指定,另外存储第一步中位移切线增量d_Ut的范数的平方值,n2。该值用来在后续步骤中计算GSP。对于剩余的增量步(增量步>1),GSP根据公式(41)计算,增量符号在根据公式(42)进行调整,即每次 GSP 值为负时必须反转预测阶段荷载比增量的符号。
之后,根据式(40)获得增量大小的调整因子J。需要指出表达式中的变量 iter存储上一步执行的迭代次数,必须将其增加1以避免被零除,因为预测的解对应于零次迭代。如果用户选择以恒定增量执行分析,则调整因子J的值设置为一。最后,根据公式(38)计算预测的荷载比增量。得到荷载率预测增量后,根据式(36)计算位移预测增量d_U(仅使用位移的切线增量),并对当前增量步的载荷比和位移增量(D_lr 和 D_U)进行更新。
迭代校正阶段,首先迭代次数的计数器iter被初始化为零,因为假设第一次校正迭代仅在预测阶段的收敛之后才开始。然后迭代循环开始于一个while循环中,该循环运行直到达到最大迭代次数或者不收敛时停止。
在迭代循环开始时,载荷比和节点位移的总值用上次迭代获得的修正增量更新,或者如果刚进入循环则用预测阶段的增量更新。外部节点力矢量 P 很容易从总载荷比lr中获得,而内部节点力矢量 F 需要在通过intForcesUL()函数针对当前节点位移进行计算。然后通过外力和内力矢量之间的差获得残余力矢量 R。
基于残余力范数的标准检查当前迭代的收敛性,如公式(43) 所示。如果与参考荷载向量的比足够小,则迭代收敛,算法退出循环进入下一个增量步。否则,算法继续进行下一次迭代校正并立即递增迭代次数inter。 荷载和位移增量校正迭代前先要选择迭代方案。如果选择标准的 Newton-Raphson 迭代,将使用更新后的构型来计算新的切线刚度矩阵,即使用在上一次迭代结束时获得的单元内力和节点位移。否则,如果选择修正Newton-Raphson 迭代法,则继续使用在预测阶段的得到的切线刚度矩阵。
位移校正的切线增量d_Ut和残余增量d_Ur分别使用参考载荷Pref和残余力R用线性系统计算。荷载比比的迭代校正选用恒定圆柱弧长法的表达式,由方程式(45)给出。最终根据方程(36)得到节点位移的迭代修正。一旦获得载荷和位移的修正值,运用其增量值来更新前增量步。最后,更新总的位移和荷载。
对于给定的位移计算内力基于UL公式通过函数intForcesUL()实现,首先初始化内力的全局向量,然后,对所有单元执行循环,计算局部坐标系下每个单元的内力矢量,将其转换为全局坐标系下的内力矢量,并将其组装至全局矢量中。在循环开始时,计算单元伸长率D_L,是通过当前单元长度 L_c 与参考配置(每个增量步开始时)的长度 L_1 之间的差值获得的。
之后,计算单元刚体旋转角度(单元与全局坐标系X轴的角度),即每个增量步开始时的角度angle_1+刚体旋转增量 rbr。当前角度在单元结构体中更新。
内力增量矢量D_f1弹性刚度矩阵与相对位移矢量(变形矢量)的乘积计算得出的。此增量添加到总内力矢量,获得局部坐标系中当前构型下的总内力fl存储在单元数据结构中,用于计算切线刚度矩阵(几何刚度矩阵)。通过将局部坐标系中的内力矢量乘以旋转矩阵,获得全局坐标系下的内力矢量。最后,使用单元索引矢量将单元内力插入到全局矢量中。
(预测阶段代码) function Result = solve(Model,Anl,Elem,Pref) % 初始化节点位移和荷载比 U = zeros(Model.neq,1); lr = 0; % 初始化result结构体,并插入初始平衡点 Result = struct('U_step',[],'U_iter',[],'lr_step',[],'lr_iter',[]); Result.U_step(:,1) = U; Result.U_iter(:,1) = U; Result.lr_step(1) = lr; Result.lr_iter(1) = lr; %===========开始增量步求解过程==================================== step = 0; while (step < Anl.max_steps) step = step + 1; % 更新参考构型下的UL方程(L_1根据上一增量步结束时的位移U进行更新;angle_1随着迭代步更新并将上一增量步结束的angle作为该步angle_1;内力fi_1同angle) % 此处更新的L_1,angle_1和phi_1会在求解内力的函数中用到intForcesUL for i = 1:Model.nel Elem(i).L_1 = elemLength(Elem(i),U); %L_1 Length from beggining of step Elem(i).angle_1 = Elem(i).angle; %angle_1 Angle with horizontal axis from beggining of step Elem(i).fi_1 = Elem(i).fi; %fi_1 Vector of internal forces in local system from beggining of step end % 切线刚度矩阵(根据Ui-1更新Ki0) [Kt,Elem] = tangStiffMtxUL(Model,Anl,Elem,U) ; %%根据i-1增量步的位结束移向量更新节点位置后得到的单元刚度矩阵(单元长度,单元角度),但返回的Elem只更新了Ke用来接下来计算内力 % 预测解位移的切线增量delta_Ui1 d_Ut = solveLinearSystem(Model,Kt,Pref);%delta_Ui1预测阶段的位移的切线增量,接下来是计算预测阶段的荷载比增量(增量步是否为第一增量步对应的荷载比增量公式不同) if (step == 1) s = 1; %第一增量步的预测阶段的增量的符号默认为正 d_lr = Anl.init_incr; %delta_lamda_11 人为规定预测阶段d_lr n2 = d_Ut'*d_Ut;%第一增量步中位移切线增量的范数的平方值,会在后续分析步计算GSP else GSP = n2 / (d_Ut'*d_Ut_1);%公式(41) % Generalized Stiffness Parameter if (GSP < 0) s = -s; %公式(42) 增量步符号 end % 增量步调整系数J % J = sqrt((Anl.trg_iter + 1) / (iter + 1));%目标迭代次数/上一增量步步的迭代次数(公式(40))必须将其增加 1 以避免被零除,因为预测的解对应于零次迭代 J = 1; %% 预测阶段荷载比增量 采用圆柱弧长法 % Extract free DOF components D_U_temp = D_U(1:Model.neqf); d_Ut_temp = d_Ut(1:Model.neqf); d_lr = J * sqrt((D_U_temp'*D_U_temp) /(d_Ut_temp'*d_Ut_temp));%公式38:圆柱弧长法 % Apply correct sign d_lr = s * d_lr; end % 荷载比要小于规定值(==1) if ((Anl.max_ratio > 0.0 && lr + d_lr > Anl.max_ratio) ||... (Anl.max_ratio < 0.0 && lr + d_lr < Anl.max_ratio)) d_lr = Anl.max_ratio - lr;%保证恰好达到最终的荷载比增量1实现荷载的全部施加 end d_U = d_lr * d_Ut;%根据公式(36)预测阶段假定残差为零因此,只有前一项切线增量 % Store predicted results d_lr_1 = d_lr; d_Ut_1 = d_Ut; d_U_1 = d_U; % 前步的载荷比和位移增量(后续会随着迭代不断更新叠加) D_lr = d_lr; D_U = d_U; % 总荷载比和位移 lr = lr + d_lr; U = U + d_U; %
(校正迭代阶段代码) % Start iterative process iter = 0; conv = 0; while (conv == 0 && iter < Anl.max_iter) % External and internal forces P = lr * Pref; [F,Elem] = intForcesUL(Model,Elem,U,D_U,1);%采用上一次迭代计算得到的Ke,并根据D_U对Ele.angle和Ele.fi进行更新 R = P - F; %残余力矢量 % Store iteration results Result.U_iter(:,size(Result.U_iter,2)+1) = U; Result.lr_iter(size(Result.lr_iter,2)+1) = lr; % Check for convergence conv = (norm(R(1:Model.neqf))/norm(Pref(1:Model.neqf)) < Anl.tol); if (conv == 1) break; end % Start/keep corrective cycle of iterations iter = iter + 1; [Kt,Elem] = tangStiffMtxUL(Model,Anl,Elem,U); %每次迭代更新,标准牛顿拉普森方法,Elem.ke更新 % Tangent and residual increments of displacements d_Ut = solveLinearSystem(Model,Kt,Pref); d_Ur = solveLinearSystem(Model,Kt,R); % 荷载比修正(公式(45))恒定弧长法-圆柱法 a = d_Ut'*d_Ut; b = d_Ut'*(d_Ur + D_U); c = d_Ur'*(d_Ur + 2*D_U);%D_U为上一迭代步的值,d_Ur为本步更新后的值 s_iter = sign(D_U'*d_Ut); d_lr = -b/a + s_iter*sqrt((b/a)^2 - c/a); %如果增量步过大可能会出现复数 if (~isreal(d_lr)) conv = -1; break; end % 公式(36) d_U = d_lr * d_Ut + d_Ur; % Increments of load ratio and displacements for current step D_lr = D_lr + d_lr; D_U = D_U + d_U; % Total values of load ratio and displacements lr = lr + d_lr; U = U + d_U; end %----------------------------------------------------------------------------------
(内力计算) function [F,Elem] = intForcesUL(Model,Elem,U,D_U,update_angle) % Initialize global vector of internal forces F = zeros(Model.neq,1); for i = 1:Model.nel % Lengths: Beginning of step, current, and step increment L_1 = Elem(i).L_1;%每个增量步开始时进行更新 L_c = elemLength(Elem(i),U); D_L = L_c - L_1; % Rigid body rotation from step beginning and current angle rbr = elemAngleIncr(Elem(i),U,D_U);%rbr带有符号,增加正值,减少负值 angle = Elem(i).angle_1 + rbr; % Update element angle if (update_angle) Elem(i).angle = angle; end % Rotation matrix from local to global coordinate system c = cos(angle); s = sin(angle); rot = [ c -s 0 0 0 0; s c 0 0 0 0; 0 0 1 0 0 0; 0 0 0 c -s 0; 0 0 0 s c 0; 0 0 0 0 0 1 ]; % Relative rotations(变形转角) r1 = D_U(Elem(i).n1.dof(3)) - rbr; r2 = D_U(Elem(i).n2.dof(3)) - rbr; % Vector of local displacements dl = [0; 0 ; r1; D_L; 0; r2];%没有y向变形,只有轴向和转动变形??? % Increment of internal forces in local system D_fl = Elem(i).ke * dl; % Total internal forces in local system fl = Elem(i).fi_1 + D_fl; % Store total internal forces in local system Elem(i).fi = fl; % Transform internal forces from local system to global system fg = rot * fl; % Assemble element internal forces to global vector gle = Elem(i).gle; F(gle) = F(gle) + fg; end end
审核编辑:刘清
-
matlab
+关注
关注
186文章
2983浏览量
231257 -
GSPM
+关注
关注
0文章
2浏览量
6131 -
MATLAB编程
+关注
关注
1文章
13浏览量
8482
原文标题:SimPC博士:几何非线性有限元基本原理及matlab编程(下)
文章出处:【微信号:sim_ol,微信公众号:模拟在线】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
MATLAB有限元分析与应用
OASYS.Suite.13.1.WINDOWS.LINUX.64通用非线性瞬态动力分析有限元软件
线性电源的基本原理是什么
有限元法的原理
膜式空气弹簧非线性弹性特性有限元分析
有限元分析及应用_曾攀
电机内电磁场的有限元计算

如何使用Matlab进行有限元分析和硬盘的选购与使用资料说明
基于Matlab有限元编程的变截面悬臂梁分析
基于六面体单元热应力问题的Matlab有限元编程求解
SimPC博士:几何非线性有限元基本原理及matlab编程
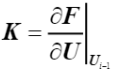




 几何非线性有限元基本原理及matlab编程
几何非线性有限元基本原理及matlab编程










评论