先说答案,这是肯定的,所有递归代码都可以转为非递归代码。
之所以所有的递归都能转为迭代算法是因为递归借助函数调用,函数调用本身就是基于调用栈这种结构实现的,只不过这一切都是自动完成的,我们当然也可以用代码手动模拟出来。
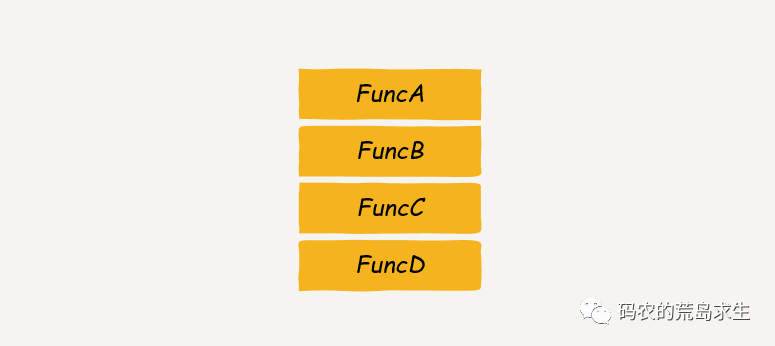
我们知道将递归调用全部展开后其实会形成一棵树,把递归转为非递归无非就是在遍历这棵树,那么遍历树就有很多技术了,基于栈的深度优先遍历Depth-first traversal,或者基于队列的广度优先遍历breadth-first traversal都是可以的:
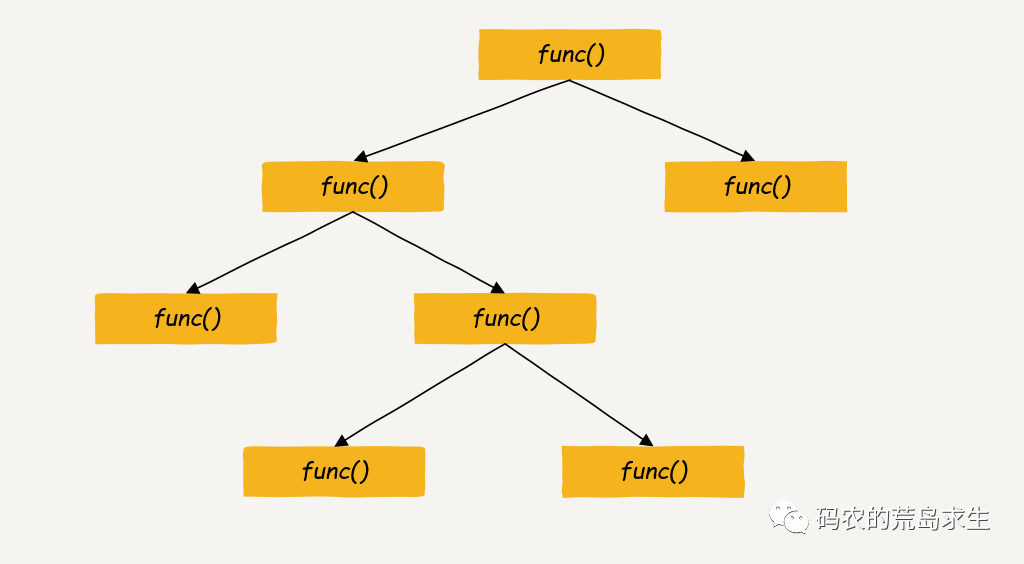
说会递归转为非递归这个话题,更理论一些的解释是这样的,不管是递归还是非递归,这两者都是图灵完备的,既然是图灵完备,那么它们在表达能力上就是等价的,不存在谁不能转为谁的问题。
只不过这存在一个难易程度的问题。
大家都知道尾递归最容易转为非递归的迭代形式,本质上是这棵树不是多叉的而是单叉的,单叉的不就退化成链表了嘛,遍历链表当然是简单的,但如果是多叉的话问题就没那么简单了, 这里最有趣的是不存在一种模板可以让我们直接用套路的形式把递归转为非递归 ,因此这里存在一个问题:为什么你要把递归转为非递归呢?因为最终你会发现将递归转为非递归无非就是你自己接手了编译器本来已经替你完成的工作, 你会发现自己在手动模拟函数调用 。
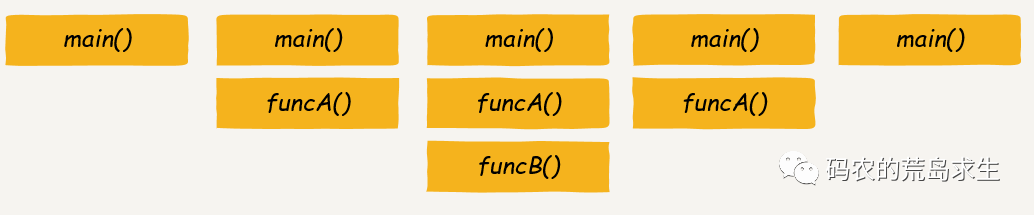
递归的优势很明显:代码简洁,容易理解和维护,其为人诟病的地方在于执行效率“可能”没有非递归版本的高,但你最好理解这句话到底在说什么,到底哪里效率就不高了?
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
相关推荐
关于递归,或许在labview中很少听过或者使用,不过了解下,算是一种娱乐吧,labview是确实支持递归的关于递归一个可以调用自己的VI就叫做递归
发表于 01-05 15:07
("LEVEL %d: n location %p\n" , n, &n);}输出如下:递归的基本原理每级递归都使用其私有变量(如例子中的n)每次函数调用都返回前一级(调用他那级
发表于 02-05 20:06
可以用循环替代,但递归这种思想符合人类思考问题的方式。在很多问题中,采用递归可以大大提高代码的可读性,而且编程容易实现。而这时如若非要才要循
发表于 02-14 22:06
我的上一遍主题写了“三个水桶等分8升水问题”,在其中提到了递归的重要性以及LabVIEW如何设置VI才能使得该VI可以实现递归调用。而最近看了下《算法的乐趣》中,看到爱因斯坦问题这一章之后,更是让我
发表于 02-19 11:52
一.NI提供的递归调用使用的步骤如下1.将VI设置成重载模式2.使用静态调用调用调用VI,实现自身调用看见下图NI自带递归方法二、如果将静态调用改成直接调用自身也可得到相同的结果,而且程序更直
发表于 05-18 10:36
Labview递归函数的使用案例,简单的1+2+3...+100求和,简单易懂,充分理解递归函数的思想
发表于 10-09 09:37
LabVIEW中使用递归算法LabVIEW支持递归吗?如何在LabVIEW中创建递归的VI?LabVIEW确实支持递归。按照下面的步骤来创建一个递归
发表于 04-17 20:11
文中提出一种通用递归算法的设计模式,并结合实例说明该模式的应用方法和有效性,为研究递归算法提供了有效的解决方案,可推广性强。同时给出了递归程序在调试过程中的一些方法和
发表于 11-03 15:04
•24次下载
LabVIEW中使用递归调用不是很方便。并且递归并不是编程必须程序结构,任何需要使用递归调用的地方,都可以用循环结构来代替。但是在某些情况下,使用递
发表于 03-25 16:39
•2次下载
之所以所有的递归都能转为迭代算法是因为递归借助函数调用,函数调用本身就是基于调用栈这种结构实现的,只不过这一切都是自动完成的,我们当然也可以用代码
![的头像]() 发表于
发表于 04-19 15:02
•2127次阅读
那么我通过一道简单的面试题,模拟面试的场景,来带大家逐步分析递归算法的时间复杂度,最后找出最优解,来看看同样是递归,怎么就写成了O(n)的代码。
![的头像]() 发表于
发表于 07-13 11:30
•2279次阅读
Python支持递归函数——即直接或间接地调用自身以进行循环的函数。递归是颇为高级的话题,并且它在Python中相对少见。然而,它是一项应该了解的有用的技术,因为它允许程序遍历拥有任意的、不可预知的形状的结构。递归甚至是简单循环
![的头像]() 发表于
发表于 02-21 14:28
•656次阅读
与原问题相似的规模较小的问题来解决,递归策略只需少量的程序就可描述出解题过程所需的多次重复计算,大大地减少了程序的代码量。
![的头像]() 发表于
发表于 02-21 15:57
•591次阅读
要说到递归如果不说栈的话,我觉得有点不合适,递归特点就是不断的调用同一个函数,如果这个函数没有一个递归界限,那么就是死循环了,所以讨论递归,就必须要讨论
![的头像]() 发表于
发表于 06-06 15:24
•1024次阅读
当我们碰到诸如需要求阶乘或斐波那契数列的问题时,使用普通的循环往往比较麻烦,但如果我们使用递归时,会简单许多,起到事半功倍的效果。这篇文章主要和大家分享一些和递归有关的经典案例,结合一些资料谈一下个人的理解,也借此加深自己对递归
![的头像]() 发表于
发表于 08-05 15:57
•346次阅读








 递归代码都转为非递归可以吗
递归代码都转为非递归可以吗











评论