一.项目背景
AQI(air Quality Index)指空气质量指数,用来衡量空气清洁或者污染程度。值
越小,表示空气质量越好。近年来因为环境问题,空气质量越来越受到人们重视。
上篇文章[AQI分析与预测(一)](http://mp.weixin.qq.com/s?__biz=MzIzODI4ODM2MA==&mid=2247486525&idx=1&sn=a92d40e0d715f9ab63563b4e8b054a0d&chksm=e93ae0bade4d69ac57407216484cdbb6d7a8a812baef1c0e4ab0d5aeae0c7f0aff9fd274127b&scene=21#wechat_redirect)我们进行了初步分析,主要分析了空气质量最好/差城市和临海城市是否空气质量优于内陆城市这两个问题,本篇我们在之前基础上继续研究如下问题。
1.空气质量受那些因素影响
2.关于空气质量验证
3.构建空气质量预测模型
二.实现过程
1.空气质量受那些因素影响
》》指标:协方差和相关系数
》》图形:热力图
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
sns.set(style="darkgrid", font_scale=1.2)
plt.rcParams["font.family"] = "SimHei"
plt.rcParams["axes.unicode_minus"] = False
warnings.filterwarnings("ignore")
#读取文件
data = pd.read_csv("data.csv")
#查看数据
data.head()

#kind:绘制图像的类型。可选值:
#scatter:散点图(默认值)。
#reg:带有回归线的散点图。
#vars:显示哪些变量之间的两两关系,默认为显示所有变量。
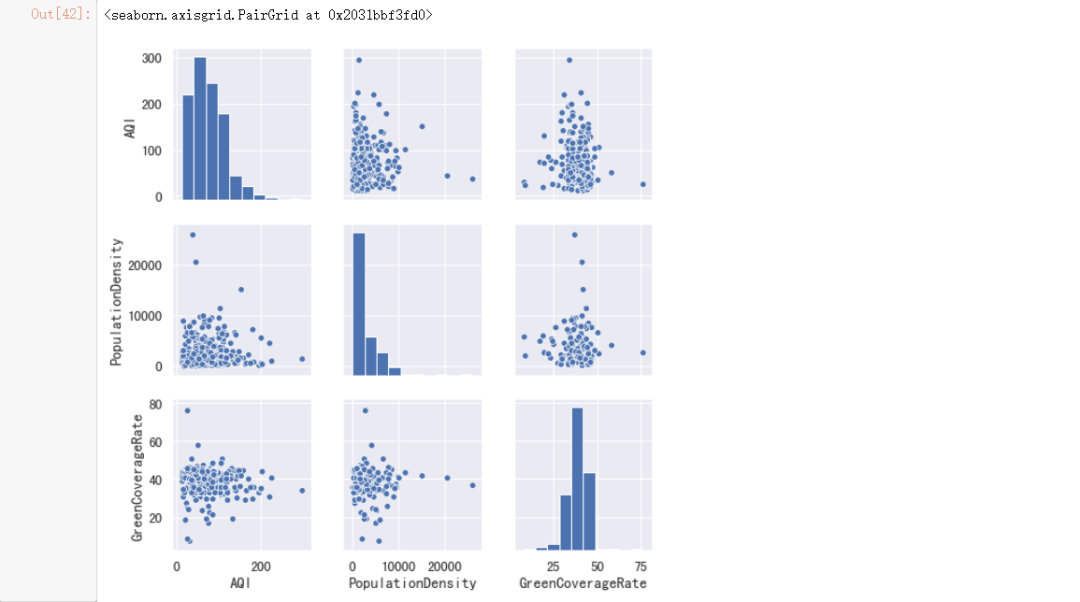
sns.pairplot(data, vars=["AQI", "PopulationDensity", "GreenCoverageRate"])

#计算相关数据
x = data["AQI"]
y = data["Precipitation"]
#计算AQI与Precipitation的协方差。
a = (x - x.mean()) * (y - y.mean())
#计算协方差
cov = np.sum(a) / (len(a) - 1)
print("协方差:", cov)


#计算AQI与Precipitation的相关系数。
corr = cov / np.sqrt(x.var() * y.var())
print("相关系数:", corr)

#pandas封装了相关方法
print("协方差:", x.cov(y))
print("相关系数:", x.corr(y))

#初始化画布
plt.figure(figsize=(15, 10))
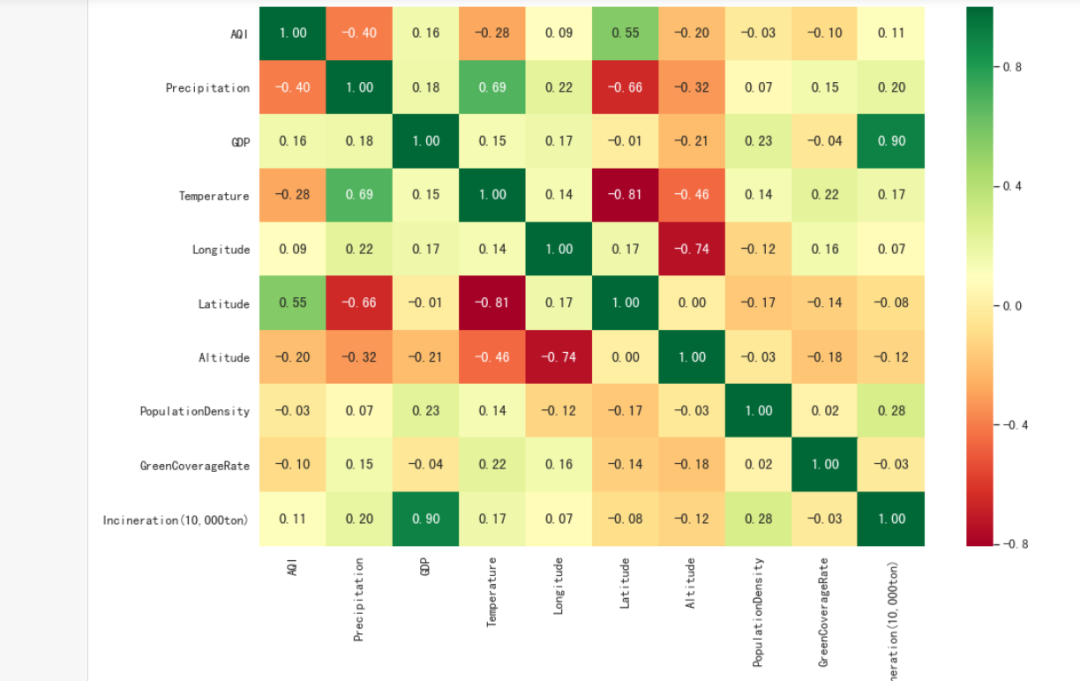
#绘制热力图
ax = sns.heatmap(data.corr(),
cmap=plt.cm.RdYlGn,
annot=True,
fmt=".2f")
结论:降雨量越多,空气质量越好;维度越低,空气质量越好
2.关于空气质量验证
》》问题:全国所有城市的空气质量指数均值在71左右,请问此结论准确吗?
》》方法:假设检验
该需求是验证样本均值是否等于总体均值,根据条件,我们可以使用单样本t检验,
置信度为95%。
#进行单样本t检验
r = stats.ttest_1samp(data["AQI"], 71)
#输出检验统计量
print("t值:", r.statistic)
#输出p值
print("p值:", r.pvalue)
结论:我们可以看到P值是大于0.05的,y因此我们无法拒绝原假设,因此接受原假设

#计算均值
mean = data["AQI"].mean()
#计算标准差
std = data["AQI"].std()
#计算置信区间
stats.t.interval(0.95, df=len(data) - 1, loc=mean, scale=std / np.sqrt(len(data)))
结论:我们就计算出全国城市平均空气质量指数,95%的可能大致在70.63~80.04之间

3.构建空气质量预测模型
》》对于一些城市,如果能够已知降雨量,温度,经纬度等指标,我们是否能够预测该
城市的空气质量指数呢?因此我们需要构建模型,预测新的数据。
》》过程:基模型构建,异常值处理后构建模型和特征选择后构建模型,将结果与基模
型进行对比,看看是否进行优化。
#进行类别转换
data["Coastal"] = data["Coastal"].map({"是": 1, "否": 0})
#统计类别数目
data["Coastal"].value_counts()
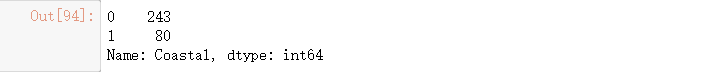
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
#City(城市名称)对预测毫无用处,删掉。
X = data.drop(["City","AQI"], axis=1)
#目标值
y = data["AQI"]
#分离测试集和训练集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
#构建基础线性回归模型
lr = LinearRegression()
#训练模型
lr.fit(X_train, y_train)
#输出训练集模型评分
print(lr.score(X_train, y_train))
#输出测试集模型评分
print(lr.score(X_test, y_test))

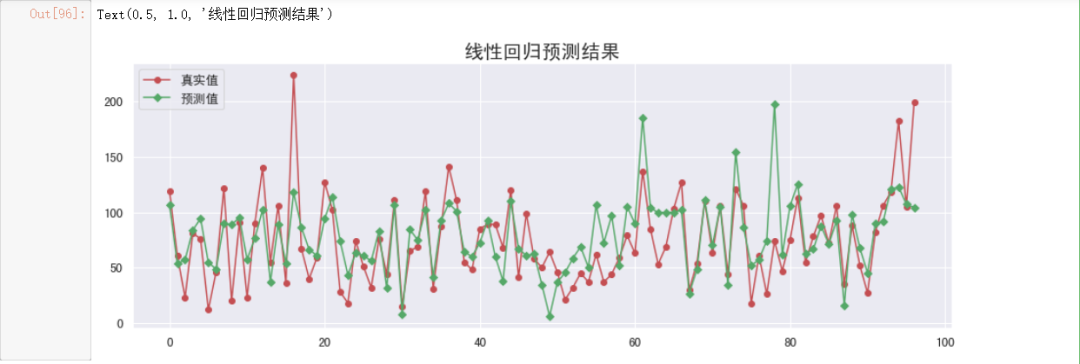
#绘制图形观察
#预测y值
y_hat = lr.predict(X_test)
#初始化画布
plt.figure(figsize=(15, 5))
#绘制真实值折线图
plt.plot(y_test.values,
"-r",
label="真实值",
marker="o")
#绘制预测值折线图
plt.plot(y_hat,
"-g",
label="预测值",
marker="D")
#设置图例
plt.legend(loc="upper left")
#设置标题
plt.title("线性回归预测结果", fontsize=20)
# Coastal是类别变量,映射为离散变量,不会有异常值。
#遍历列
for col in X.columns.drop("Coastal"):
#对数值型数据进行判断
if pd.api.types.is_numeric_dtype(X_train[col]):
#获取分位数
quartile = np.quantile(X_train[col], [0.25, 0.75])
#计算IQR
IQR = quartile[1] - quartile[0]
#计算正常数值下限
lower = quartile[0] - 1.5 * IQR
#计算正常数值上限
upper = quartile[1] + 1.5 * IQR
#用边界值进行填充异常值
X_train[col][X_train[col] < lower] = lower
X_train[col][X_train[col] > upper] = upper
X_test[col][X_test[col] < lower] = lower
X_test[col][X_test[col] > upper] = upper
#训练模型
lr.fit(X_train, y_train)
#去除异常值后评估模型效果
print(lr.score(X_train, y_train))
print(lr.score(X_test, y_test))
结论:去除异常值后所构建模型效果相比之前有所改进

#对数据进行标准化处理,
from sklearn.preprocessing import StandardScaler
#数据标准化
s = StandardScaler()
#对训练集进行标准化
X_train_scale = s.fit_transform(X_train)
#对测试集进行标准化
X_test_scale = s.transform(X_test)
#对数据进行特征选择,目的是提高模型准确率和训练速度
REFCV方法
》》RFE(REcursive feature elimination):递归特征消除,用来对特征进行重要性评级
》》CV(Cross Validation):交叉验证,通过交叉验证,选择最佳数量特征
具体过程如下:
RFE阶段:
1.初始特征集为所有可用特征
2.使用当前特征集进行建模,然后计算每个特征的重要性
3.删除最不重要的一个或者多个特征,更新特征集
4.跳到步骤2,直到完成所有特征集重要性评级
CV阶段
1.根据REF阶段确定的特征重要性,依次选择不同数量特征
2.对选定的特征集进行交叉验证
3.确定平均分最高的特征数量,完成特征选择。
from sklearn.feature_selection import RFECV
#estimator:要操作的模型。
#step:每次删除的变量数。
#cv:使用的交叉验证折数。
#n_jobs:并发的数量。
#scoring: 评估的方式。
rfecv = RFECV(estimator=lr,
step=1,
cv=5,
n_jobs=-1,
scoring="r2")
rfecv.fit(X_train_scale, y_train)
#返回经过选择之后,剩余的特征数量。
print(rfecv.n_features_)
#返回经过特征选择后,使用缩减特征训练后的模型。
print(rfecv.estimator_)
#返回每个特征的等级,数值越小,特征越重要。
print(rfecv.ranking_)
#返回布尔数组,用来表示特征是否被选择。
print(rfecv.support_)
#返回对应数量特征时,模型交叉验证的评分。
print(rfecv.grid_scores_)

#绘制图形
plt.plot(range(1, len(rfecv.grid_scores_) + 1),
rfecv.grid_scores_,
marker="o")
#设置x轴标签
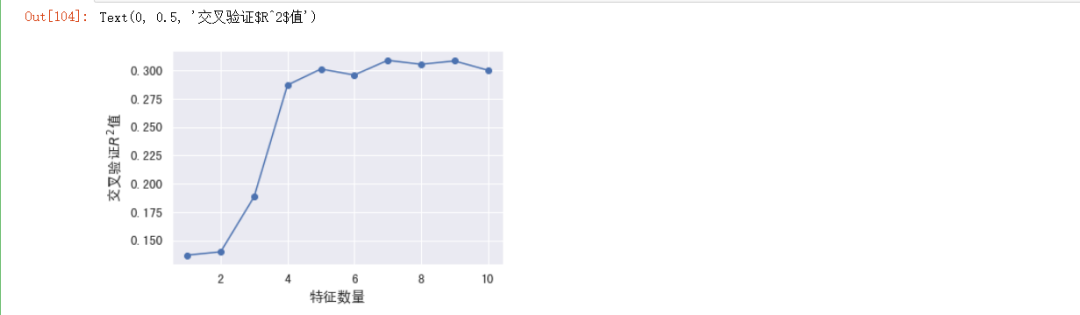
plt.xlabel("特征数量")
#设置y轴标签
plt.ylabel("交叉验证$R^2$值")
print("剔除的变量:", X.columns.values[~rfecv.support_])
#应用到训练集
X_train_eli = rfecv.transform(X_train_scale)
#应用到测试集
X_test_eli = rfecv.transform(X_test_scale)
#输出模型评分
print(rfecv.estimator_.score(X_train_eli, y_train))
print(rfecv.estimator_.score(X_test_eli, y_test))

#获取列名与对应的权重,构成一个元组,作为列表的元素。
li = list(zip(X.columns.values[rfecv.support_], rfecv.estimator_.coef_))
#根据权重的绝对值,对列表进行降序排列。
li.sort(key=lambda x: abs(x[1]), reverse=True)
#转换为Series
s = pd.Series(dict(li))
#初始化画布
plt.figure(figsize=(15, 5))
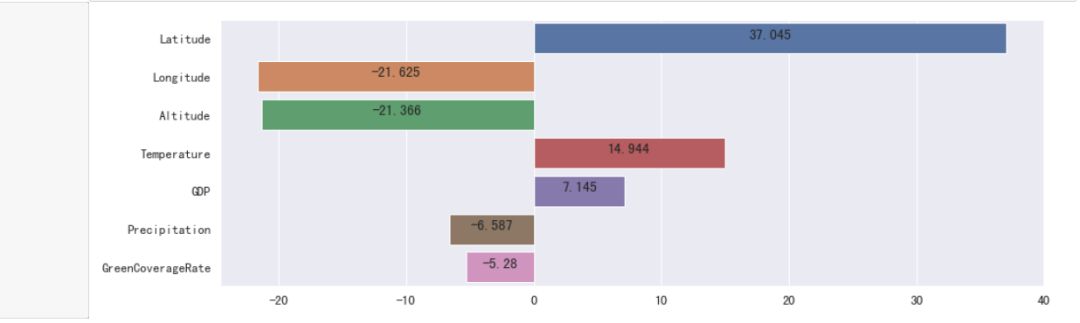
#绘制柱状图
ax = sns.barplot(y=s.index, x=s.values)
for y, x in enumerate(s):
#绘制标注
t = ax.text(x / 2, y, round(x, 3))
#设置居中对齐
t.set_ha("center")
#显示图形
plt.show()
from sklearn.preprocessing import KBinsDiscretizer
#KBinsDiscretizer K个分箱的离散器。用于将数值(通常是连续变量)变量进行区间离散化操作。
#n_bins:分箱(区间)的个数。
#encode:离散化编码方式。分为:onehot,onehot-dense与ordinal。
# onehot:使用独热编码,返回稀疏矩阵。
# onehot-dense:使用独热编码,返回稠密矩阵。
# ordinal:使用序数编码(0,1,2……)。
#strategy:分箱的方式。分为:uniform,quantile,kmeans。
#uniform:每个区间的长度范围大致相同。
#quantile:每个区间包含的元素个数大致相同。
#kmeans:使用一维kmeans方式进行分箱。
#对数据进行分箱操作
k=KBinsDiscretizer(n_bins=[4, 5, 10, 6],
encode="onehot-dense",
strategy="uniform")
#定义离散化的特征。
discretize=["Longitude", "Temperature", "Precipitation", "Latitude"]
#训练集数据转换为DataFrame
X_train_eli=pd.DataFrame(data=X_train_eli, columns=X.columns[rfecv.support_])
#测试集数据转换为DataFrame
X_test_eli=pd.DataFrame(data=X_test_eli, columns=X.columns[rfecv.support_])
#应用到训练集
r=k.fit_transform(X_train_eli[discretize])
r=pd.DataFrame(r, index=X_train_eli.index)
#获取除离散化特征之外的其他特征。
X_train_dis=X_train_eli.drop(discretize, axis=1)
#将离散化后的特征与其他特征进行重新组合。
X_train_dis=pd.concat([X_train_dis, r], axis=1)
#对测试集进行同样的离散化操作。
r=pd.DataFrame(k.transform(X_test_eli[discretize]), index=X_test_eli.index)
X_test_dis=X_test_eli.drop(discretize, axis=1)
X_test_dis=pd.concat([X_test_dis, r], axis=1)
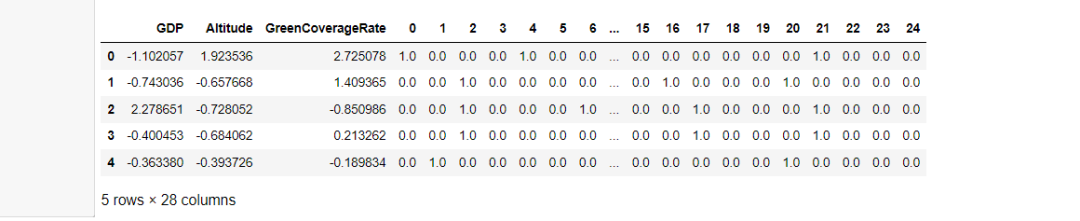
#查看转换之后的格式。
display(X_train_dis.head()
#训练模型
lr.fit(X_train_dis, y_train)
#去除异常值后评估模型效果
print(lr.score(X_train_dis, y_train))
print(lr.score(X_test_dis, y_test))
结论:离散化后模型效果进一步提升

声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
环境
+关注
关注
0文章
125浏览量
16206 -
空气质量
+关注
关注
0文章
37浏览量
8286
发布评论请先 登录
相关推荐
零售数据分析之销售预测一:我们图的到底是什么?
一个目标,定一个参考,当实际与预测差异较大时,我们可以去寻找并分析原因;2、作为标准,结合库存,作为补货的参考。在刚才的实践中,我们会发现预测的偏差率还是比较大的,那为什么呢?因为我们
发表于 09-08 14:23
微型空气质量监测仪【恒美仪器HM-AQI】解决方案
微型空气质量监测仪【恒美仪器HM-AQI】是根据十三五及各地大气污染监测治理政策生产的新型空气质量在线多参数监测系统,微型空气质量监测仪【恒美仪器HM-AQI】严格按照国家标准对四气(CO、SO2、NO
发表于 05-19 10:20
•700次阅读
MAX6921AQI+ PMIC - 显示驱动器
电子发烧友网为你提供Maxim(Maxim)MAX6921AQI+相关产品参数、数据手册,更有MAX6921AQI+的引脚图、接线图、封装手册、中文资料、英文资料,MAX6921AQI+真值表,MAX6921
发表于 02-10 20:04

MAX6921AQI+T PMIC - 显示驱动器
电子发烧友网为你提供Maxim(Maxim)MAX6921AQI+T相关产品参数、数据手册,更有MAX6921AQI+T的引脚图、接线图、封装手册、中文资料、英文资料,MAX6921AQI+T真值表,MAX6921
发表于 02-10 20:14

如何改善AQI空气质量监测站的状况-欧森杰
随着大气污染的日益严重,AQI空气质量监测站的状况也日趋恶化。本文将从硬件、软件、人员等多个角度,给出具体的建议,改善AQI空气质量监测站的状况。 一、硬件方面 1.1、AQI空气质量监测站的设备
预测分析介绍及行业应用案例
汽车制造商 1、预测需求和预测供应商绩效 问题:一家汽车制造商希望预测需求、优化库存水平并预测供应商绩效。 目标:提高效率并改进供应链管理。 解决方案:通过
AQI空气质量监测站的重要性-欧森杰
随着交通工具的发展,工业化的进步,空气污染问题日益突出,因此,AQI空气质量监测站的重要性也不容忽视。 一、AQI空气质量监测站的定义 AQI空气质量监测站是指建立在城市或者大中城市等地区,用于定期
AQI空气质量监测站——保护空气质量的重要一环
空气污染,是当今社会最严重的环境问题之一,也是人们最关心的环境问题。为了保护空气质量,AQI空气质量监测站至关重要。 一、AQI空气质量监测站的定义 AQI(Air Quality Index
电磁轨迹预测分析系统
智慧华盛恒辉电磁轨迹预测分析系统是一个专门用于预测和分析电磁运动轨迹的系统。该系统结合了电磁学、运动学、数据分析以及可能的人工智能或机器学习
电磁轨迹预测分析系统设计方案
智慧华盛恒辉电磁轨迹预测分析系统的设计方案是一个综合性的项目,它结合了电磁学、运动学、数据分析以及可能的人工智能或机器学习技术,以实现对电磁运动轨迹的精确预测和深入




 AQI分析与预测-2
AQI分析与预测-2










评论