1.1 傅里叶变换
1.1.1 傅里叶变换概述
傅里叶变换是一种可以将满足某个条件的函数表示成三角函数(正弦或余弦)表示的线性组合,最初,傅里叶分析是作为热过程解析分析的工具被提出的,在电路中,这是一种分析非正弦周期信号的最便捷的工具,傅里叶是法国数学家和物理学家,在1807年的法国科学学会上发表了运用正弦曲线来描述温度分布,但是论文中有一个具有争议性的判定,即任何连续周期信号都可以由一组适当的正弦曲线组合而成,当时拉普拉斯与其他审查者投票通过并要发表这个论文,但是拉格朗日认为傅里叶提供的方法无法表示带有棱角的信号,由于一些原因,这篇论文直到拉格朗日去世15年后才被发表,其实拉格朗日当时的想法是对的,正弦曲线的确无法组合一个带有棱角的信号,但是我们可以采用正弦曲线组合成的信号来无限的逼近这个信号,直到两种信号不存在能量差别。
通过上面的描述可以得到一个结论,傅里叶变换是一种将不规则信号通过正弦信号的线性组合表示出来的方法,但是为什么不用方波或者三角波来表示原信号呢,这是因为分解信号的方法是无穷的,但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单,因为正余弦拥有原信号所不具有的性质:正弦曲线保真度。一个正弦曲线信号输入后,输出的仍是正弦曲线,只有幅度和相位可能发生变化,但是频率和波的形状仍是一样的。且只有正弦曲线才拥有这样的性质,正因如此我们才不用方波或三角波来表示。
我们从物理系统的特征信号角度来解释为什么不能用其他信号的线性组合来表示原始信号,我们生活中常见的现象大多属于 线性时不变系统 (输入信号与输出信号满足线性关系,且系统参数不随时间变换),无论你采用微分方程或者传递函数还是状态空间,所以可以说正弦信号是系统的特征向量,当然指数信号也是系统的特征向量,用于标识能量的衰减与累计,系统中的衰减或扩散现象大多数是指数形式或者复指数形式,但是如果输入的是方波或者三角波,那输出就不一定是什么形式了,所以,除了指数信号与正弦信号外其他信号都不是线性系统的特征信号。
1.1.2 时域与频域
从我们出生开始,我们看到的世界都是以时间贯穿,人的身高走势,汽车的轨迹都会随着事件发生改变,这种以时间作为参照来观察分析动态世界的方法就属于时域分析,频域则是描述信号在频率方面特性时用到的一种坐标系,频域不是真实存在的,只是一种数学构建的领域,是一个遵循特定规则的数学范畴,正弦信号是频域中唯一存在的波形,即正弦信号是对频域的描述。
1.1.3 定义

也就是说我们只需要求出上面的几个参数的值,就可以根据定义式将函数转化为傅里叶级数的形式。与傅里叶级数相对应的就是傅里叶变换,这个定义式就简单的多。
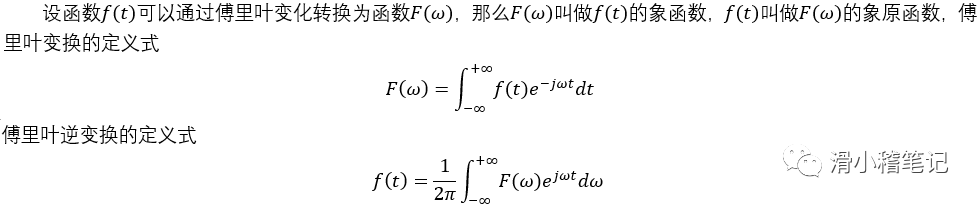
根据上面的两个公式可以发现,傅里叶变换后的象函数是以频率作为自变量的函数,而逆变换后的函数则是以时间作为自变量的函数,我们将象函数用图像的形式表示出来就成了自变量是频率的二维图像,这个图像就称为频谱图。

1.2 频域图像
在电路分析基础中,傅里叶经常被用于分析非正弦周期信号电路中,即讲一个输入激励构建数学模型,采用积分的方式转化为傅里叶级数,通过计算每个频率状态下的电参数最终分析电路整体的电参数,这就不仅需要最终的级数形式,还需要频域图像来辅助分析,在这里,我们采用MATLAB来把上面例题中的频域图像绘制出来,MATLAB的源代码如下:
clc
clear
%系数计算(用于构建傅里叶级数)
syms t n;
m = 100 ; %高次谐波叠加次数
T = 2 ; %信号的周期
f = t^2 ; %函数表达式
a0 = int( f, t, -T/2, T/2 )/T ;
an = int( f*cos(n*pi*t), t, -T/2, T/2 ) ;
bn = int( f*sin(n*pi*t), t, -T/2, T/2 ) ;
%转换定义式的形式
n = -round(T+1):1:round(T+1);
anVal = eval( an ) ; %生成an系数矩阵
bnVal = eval( bn ) ; %生成bn系数矩阵
An = sqrt( anVal.^2+bnVal.^2 ) ; %幅值开平方计算
An( round( length(n)/2 ) ) = a0 ;
phi = atan( -bnVal./anVal ) ; %相位计算
phi( round( length(n)/2 ) ) = 0 ;
%绘制幅度谱
figure(1);
subplot( 2, 1, 1 ) ;
stem( n, An ) ;
title( '幅度谱' ) ;
xlabel( 'n' ) ;
ylabel( 'An' ) ;
%绘制相位谱
subplot( 2, 1, 2 ) ;
plot( n, phi ) ;
title( '相位谱' ) ;
xlabel( 'n' ) ;
ylabel( '¦×n' ) ;
%高次谐波拟合函数曲线
figure( 2 ) ;
t = -T: 0.01: T ;
f = a0 ;
for n=1:m
f = f+eval(an)*cos(n*pi.*t);
f = f+eval(bn)*sin(n*pi.*t);
end
plot( t, f ) ;
title( strcat( num2str( n ), '次谐波叠加') ) ;
xlabel( 't' ) ;
ylabel( 'f(t)' ) ;
最终仿真的结果如下图所示。
1.3 DFT算法的MATLAB实现
傅里叶变换主要分为4类:
(1)傅里叶级数:将周期性连续函数转换为离散频率点
(2)连续傅里叶变换:将连续函数变换为连续频率函数
(3)离散时间傅里叶级数DFS:将离散函数变换为连续频率的函数
(4)离散傅里叶变换DFT:将有限长离散函数变换为离散频率点上的函数
利用MATLAB自带的fft函数实现DFT运算,源代码如下。
%45点采样
subplot( 2, 2, 1 );
N = 45 ;
n = 0:N-1 ;
t = 0.01*n ;
q = n*2*pi/N ;
x = 2*sin(4*pi*t)+5*cos(8*pi*t) ;
y = fft( x, N ) ;
plot( q, abs(y) ) ;
title('DFT N=45')
%50点采样
subplot( 2, 2, 2 ) ;
N = 50 ;
n = 0:N-1 ;
t = 0.01*n ;
q = n*2*pi/N ;
x = 2*sin(4*pi*t)+5*cos(8*pi*t) ;
y = fft( x, N ) ;
plot( q, abs(y) ) ;
title('DFT N=50')
%55点采样
subplot( 2, 2, 3 ) ;
N = 55 ;
n = 0:N-1 ;
t = 0.01*n ;
q = n*2*pi/N ;
x = 2*sin(4*pi*t)+5*cos(8*pi*t) ;
y = fft( x, N ) ;
plot( q, abs(y) ) ;
title('DFT N=55')
%60点采样
subplot( 2, 2, 4 ) ;
N = 60 ;
n = 0:N-1 ;
t = 0.01*n ;
q = n*2*pi/N ;
x = 2*sin(4*pi*t)+5*cos(8*pi*t) ;
y = fft( x, N ) ;
plot( q, abs(y) ) ;
title('DFT N=60')
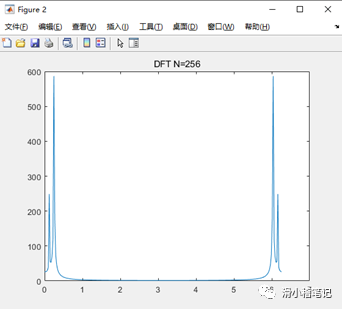
MATLAB运行截图如下所示。
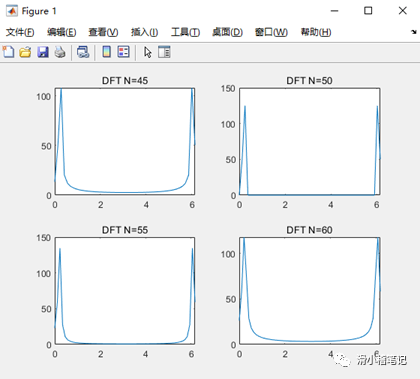
我们进一步增加截取长度与DFT点数,例如增加到256:
N = 256 ;
n = 0:N-1 ;
t = 0.01*n ;
q = n*2*pi/N ;
x = 2*sin(4*pi*t)+5*cos(8*pi*t) ;
y = fft( x, N ) ;
plot( q, abs(y) ) ;
title('DFT N=256')
此时信号的频谱如下图所示。
假设采样频率f=100Hz,采样间隔T=0.01s时,取样点N的值越大,则谱分辨率F=f/N越小,说明此时分辨率越高,加入采样点为256时,既可以实现两个不同频率信号的区分。
1.4 FFT算法的MATLAB实现
FFT是离散傅立叶变换DFT的快速计算方法,适用于离散信号,并且注意变换后的点数与信号的采样点数一致,尽管可以将信号补0,但补0不能提高频域的分辨率。matlab中提供了函数fft做一维的FFT。
(1)时域谱和频域谱是相互对应;时域的信号长度,决定频域的采样间隔,它们成导数关系;
(2)时域中信号有N点,每点间隔dt,所以时域信号长度为Ndt;那么频谱每点的间隔就是1/(Ndt)。
clc
clear
N = 256 ;
dt = 0.02 ;
n = 0:N-1 ;
t = n*dt ;
x = sin(2*pi*t) ;
m = N ;
a = zeros( 1, m ) ;
b = zeros( 1, m ) ;
c = zeros( 1, m ) ;
for k=0:m-1
for i=0:N-1
a( k+1 )= a( k+1 )+2/N*x( i+1 )*cos( 2*pi*k*i/N ) ;
b( k+1 )= b( k+1 )+2/N*x( i+1 )*sin( 2*pi*k*i/N ) ;
end
c( k+1 ) = sqrt( a( k+1 )^2+b( k+1 )^2 ) ;
end
%时域图
subplot( 2, 1, 1 ) ;
plot( t, x ) ;
title( '原始信号' ) ;
xlabel( 't' ) ;
ylabel( 'f(t)' ) ;
%频域图像
f = ( 0:m-1 )/( N*dt ) ;
subplot( 2, 1, 2 ) ;
plot( f, c ) ;hold on
title( 'Fourier' ) ;
xlabel( '频率/HZ' ) ;
ylabel( '幅值' ) ;
%计算频率
ind = find( c==max(c), 1, 'first' ) ; %查找频率第一个最大值
x0 = f( ind ); %得到横坐标
y0 = c( ind ); %得到纵坐标
plot( x0, y0, 'ro' );hold off
text( x0+1, y0-0.1, num2str( x0, '频率=%f' ) ) ;
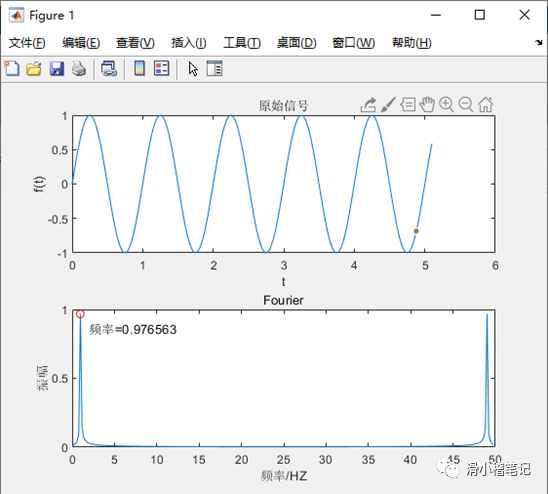
MATLAB运行结果如下图所示。
1.3基于51单片机的频谱设计
1.3.1 功能
我们现在使用51单片机来实现频谱的显示,通过输入音频信号来输出对应的频段的幅值,这次选用的是STC12C5A60S2,运行时钟33MHz,内置ADC采样,利用LED组成点阵显示屏幕,通过ADC不停的采样音频数据,将数据转换为频域幅值显示在LED上面。
1.3.2 原理图分析
(1)最小系统电路
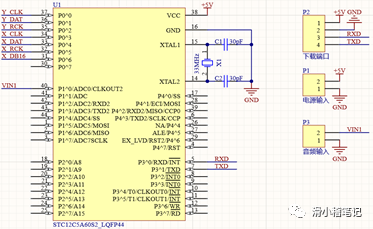
单片机系统采用国产的51单片机,在之前的51单片机中我们已经具体了解过51单片机的应用,这里不再详细赘述,我们这次采用的是33MHz的晶振,STC12C系列相对于传统的51单片机来说,运行速度快了接近12倍,可以运行256位的FFT算法,程序采用串口的方式烧录进去,其中P1口可以设置为ADC输入口,内置8通道10位ADC转换器,采用直流5V供电。
(2)LED驱动电路
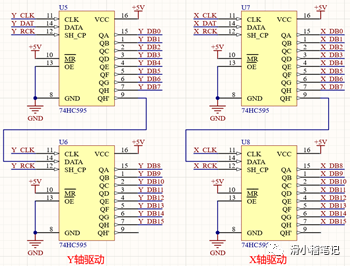
由于我们使用的单片机只有44个引脚,实际能用的IO端口仅有35个,而我们是用的是17×16的矩阵,需要33个端口,去掉1组串口,1个ADC,剩下的端口速度各不相同,已经无法满足驱动的需要,所以采用74HC595芯片作为驱动电路,74HC595是一个可以将串行数据转换为并行数据的芯片,并且可以通过级联的方式输出数据,我们采用2片595芯片的级联来实现串行数据转16位并行的的效果,其余的1位数据通过IO口来达到控制的目的。74HC595的时序图如下图所示。
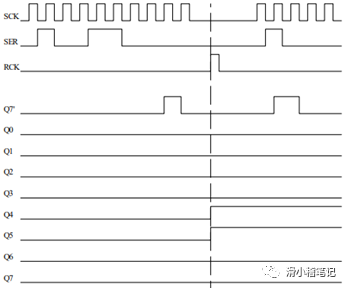
(3)点阵显示电路
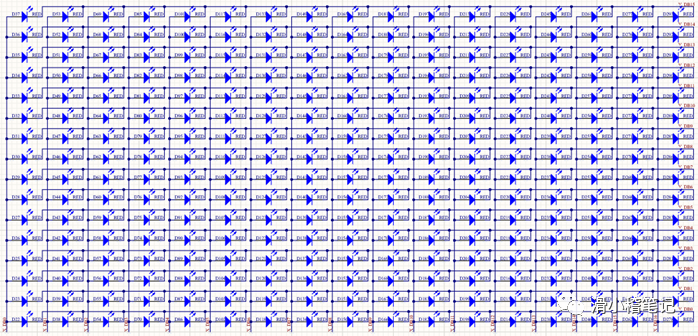
这里采用17×16的点阵作为显示,这种点阵连接的方式可以通过控制17+16=33个端口来实现17*16=272个LED亮灭的控制。
-
matlab
+关注
关注
185文章
2976浏览量
230559 -
线性
+关注
关注
0文章
198浏览量
25162 -
傅里叶变换
+关注
关注
6文章
441浏览量
42607
发布评论请先 登录
相关推荐
学习傅里叶变换意义和方法
DSP变换运算-傅里叶变换
小波变换比傅里叶变换好在哪里_小波变换与傅里叶变换详解

MATLAB学习笔记之傅里叶变换2
傅里叶变换如何用于深度学习领域

傅里叶变换基本性质 傅里叶变换本质 傅里叶变换的应用
傅里叶变换的定义 傅里叶变换的意义
傅里叶变换基本原理及在机器学习应用





 MATLAB学习笔记之傅里叶变换1
MATLAB学习笔记之傅里叶变换1










评论