有个事情可能会让初学者惊讶:神经网络模型并不复杂!『神经网络』这个词让人觉得很高大上,但实际上神经网络算法要比人们想象的简单。
这篇文章完全是为新手准备的。我们会通过用Python从头实现一个神经网络来理解神经网络的原理。本文的脉络是:
- 介绍了神经网络的基本结构——神经元;
- 在神经元中使用S型激活函数;
- 神经网络就是连接在一起的神经元;
- 构建了一个数据集,输入(或特征)是体重和身高,输出(或标签)是性别;
- 学习了损失函数和均方差损失;
- 训练网络就是最小化其损失;
- 用反向传播方法计算偏导;
- 用随机梯度下降法训练网络。
***01 ***砖块:神经元
首先让我们看看神经网络的基本单位,神经元。神经元接受输入,对其做一些数据操作,然后产生输出。例如,这是一个2-输入神经元:
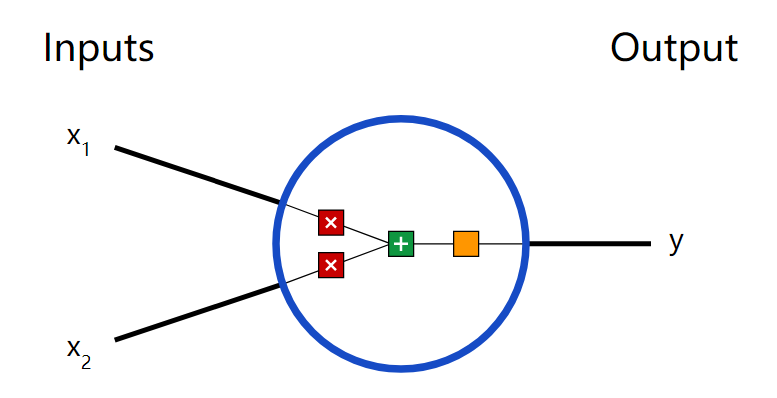
这里发生了三个事情。首先,每个输入都跟一个权重相乘(红色):
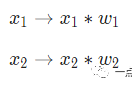
然后,加权后的输入求和,加上一个偏差b(绿色):
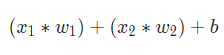
最后,这个结果传递给一个激活函数f:
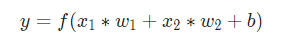
激活函数的用途是将一个无边界的输入,转变成一个可预测的形式。常用的激活函数就就是S型函数:
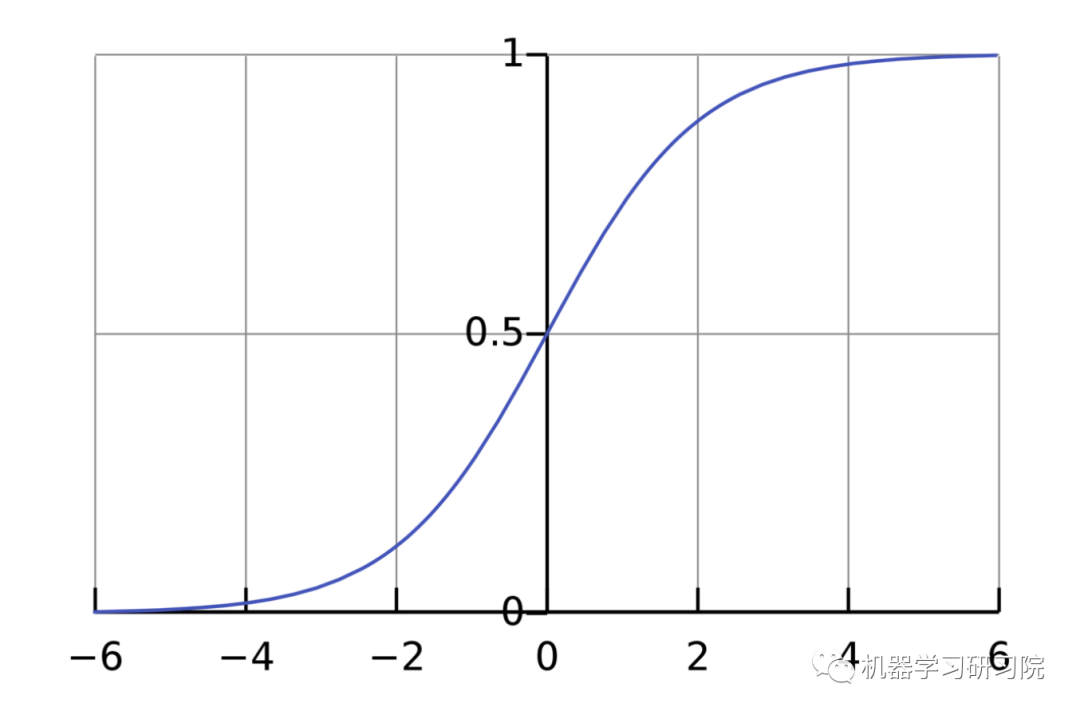
S型函数的值域是(0, 1)。简单来说,就是把(−∞, +∞)压缩到(0, 1) ,很大的负数约等于0,很大的正数约等于1。
***02 ***一个简单的例子
假设我们有一个神经元,激活函数就是S型函数,其参数如下:
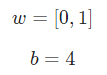
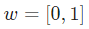 就是以向量的形式表示
就是以向量的形式表示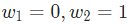 。现在,我们给这个神经元一个输入
。现在,我们给这个神经元一个输入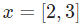 。我们用点积来表示:
。我们用点积来表示:
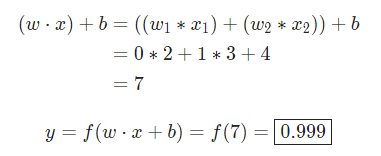
当输入是[2, 3]时,这个神经元的输出是0.999。给定输入,得到输出的过程被称为前馈(feedforward)。
***03 ***编码一个神经元
让我们来实现一个神经元!用Python的NumPy库来完成其中的数学计算:
import numpy as np
defsigmoid(x): # 我们的激活函数: f(x) = 1 / (1 + e^(-x)) return 1 / (1 + np.exp(-x))
classNeuron: def__init__(self, weights, bias): self.weights = weights self.bias = bias
deffeedforward(self, inputs): # 加权输入,加入偏置,然后使用激活函数 total = np.dot(self.weights, inputs) + self.bias return sigmoid(total)
weights = np.array([0, 1]) # w1 = 0, w2 = 1bias = 4 # b = 4n = Neuron(weights, bias)
x = np.array([2, 3]) # x1 = 2, x2 = 3print(n.feedforward(x)) # 0.9990889488055994***04 ***把神经元组装成网络
所谓的神经网络就是一堆神经元。这就是一个简单的神经网络:
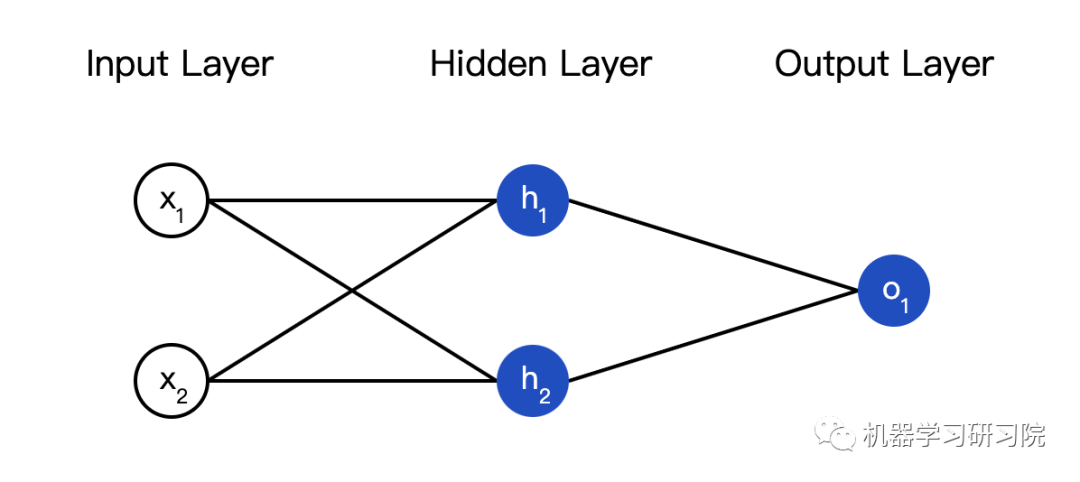
这个网络有两个输入,一个有两个神经元(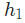 和
和 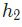 )的隐藏层,以及一个有一个神经元(
)的隐藏层,以及一个有一个神经元(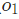 )的输出层。要注意,
)的输出层。要注意,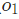 输入就是
输入就是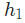 和
和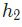 的输出,这样就组成了一个网络。
的输出,这样就组成了一个网络。
隐藏层就是输入层和输出层之间的层,隐藏层可以是多层的。
-
神经网络
+关注
关注
42文章
4793浏览量
102044 -
神经元
+关注
关注
1文章
368浏览量
18666 -
python
+关注
关注
56文章
4821浏览量
85674
发布评论请先 登录
相关推荐
labview BP神经网络的实现
卷积神经网络如何使用
【案例分享】ART神经网络与SOM神经网络
人工神经网络实现方法有哪些?
如何构建神经网络?
基于BP神经网络的PID控制
卷积神经网络一维卷积的处理过程
用Python从头实现一个神经网络来理解神经网络的原理2
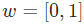
用Python从头实现一个神经网络来理解神经网络的原理3

用Python从头实现一个神经网络来理解神经网络的原理4






 用Python从头实现一个神经网络来理解神经网络的原理1
用Python从头实现一个神经网络来理解神经网络的原理1










评论