什么是模糊算法

3.1 概述

所谓模糊控制，就是对难以用已有规律描述的复杂系统，采用自然语言（如大，中，小）加以描述，借助定性的，不精确的以及模糊的条件语句来表达，模糊控制是一种基于语言的智能控制。

传统的自动控制器的综合设计都要建立在被控对象准确的数学模型（即传递函数模型或状态空间模型）的基础上，但是实际上，很多系统的影响因素很多，通常找出精确的数学模型，这种情况下，模糊控制的诞生就显得意义重大，因为模糊控制不需要建立数学模型，不需要预先知道过程精确的数学模型。模糊控制与传统的PID控制，具有如下优点：

（1）无需知道被控对象的数学模型

（2）反映人类智慧思维的智能控制

（3）易被人们所接受，是一种语言变量控制器

（4）构造容易，从属于智能控制的范畴，尤其适用于非线性，时变，滞后系统的控制

（5）抗干扰能力强，响应速度快，并对系统参数的变化有较强的鲁棒性

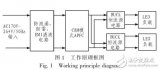
3.1.1 工作原理

把各种传感器测出的精确量转换为适用于模糊运算的模糊量，然后将这些量在模糊控制器中加以运算，最后再将运算结果中的模糊量转换为精确量，以便对各执行器进行具体的操作控制，这就说明在模糊控制中，存在着一个模糊量与精确量之间相互转化的问题，如下图所示：

模糊控制原理图如下图所示：

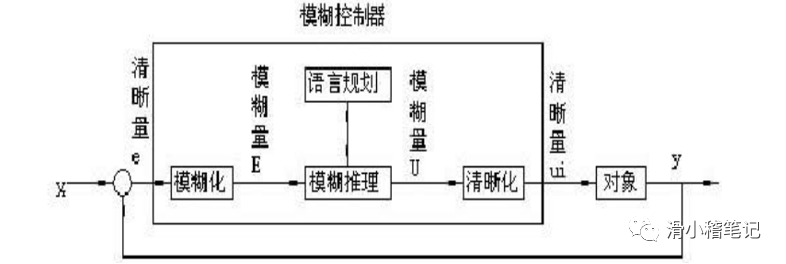
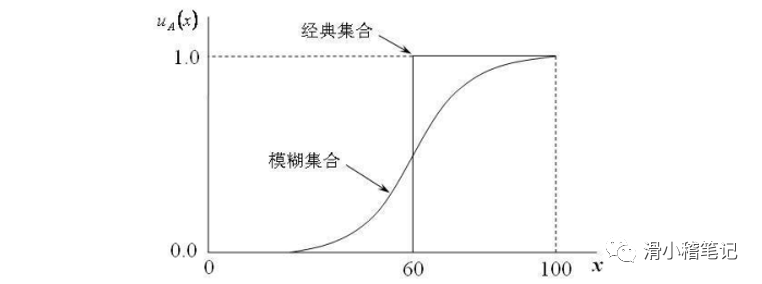
3.1.2 模糊语言集

模糊语言集用表示，一般有={负大，负中，负小，零，正小，正中，正大}，用模糊语言变量E来描述偏差，或者用符号表示：

负大：Negative Big，简称NB

负中：Negative Medium，简称NM

负小：Negative Small，简称NS

零：Zero，简称ZE

正小：Positive Small，简称PS

正中：Positive Medium，简称PM

正大：Positive Big，简称PB

3.1.3 隶属函数

各参数相对应子集的隶属函数分别由不同的函数族决定，参数的相应子集指该参数被人为地划分成的等级所构成的一组模糊集合，相应子集的多少，由控制精度决定，例如，参数“温差”的相应子集可以是“正大，正中，负小，负大”，也可以是“正大，正中，正小，负小，负中，负大”，后者比前者模糊子集多，所以控制精度更高（在其他相同条件的情况下）。

常用的隶属函数如下所示。

（1）z型隶属度函数zmf

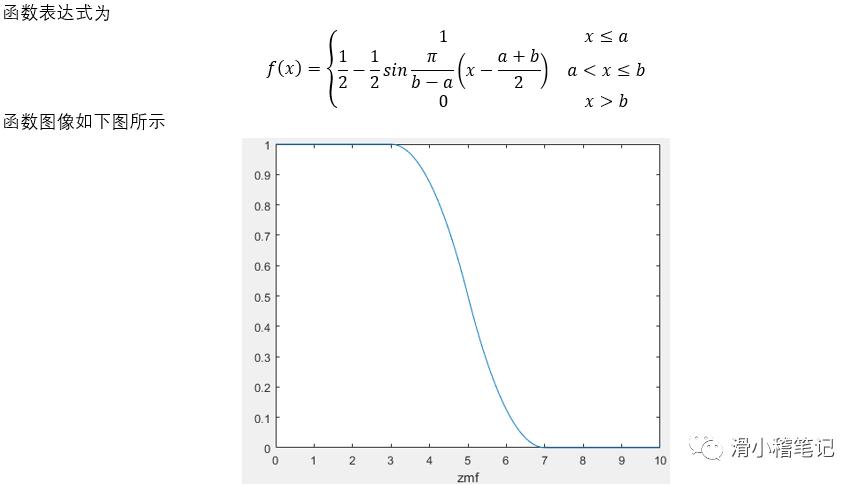
（2）S型隶属度函数smf

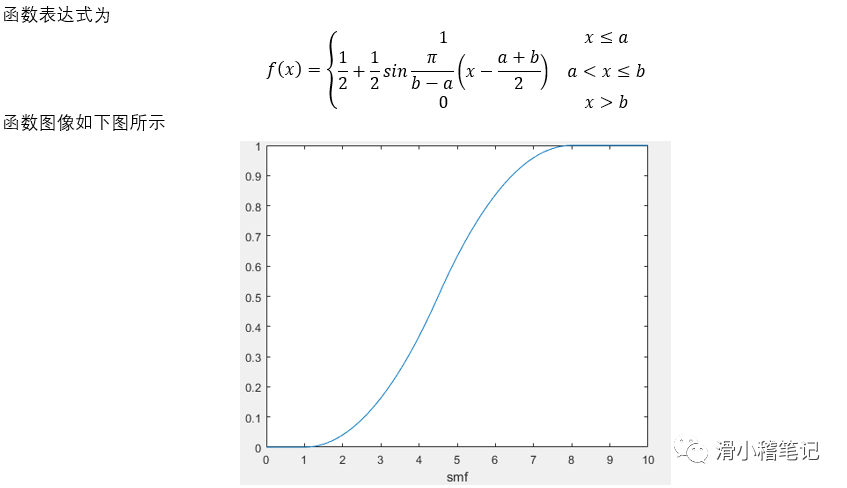
（3）三角形隶属度函数trimf

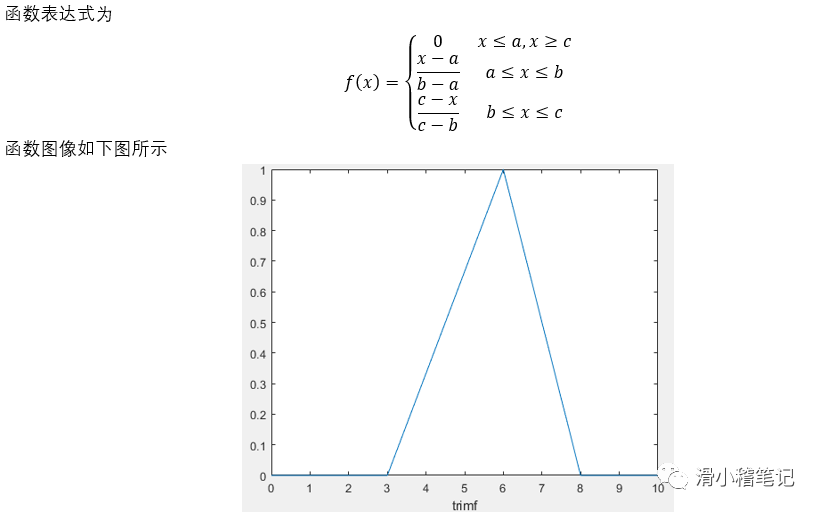
**3.2 **模糊控制数学基础

3.2.1 模糊控制集合的代数运算

3.2.2 模糊关系

（1）普通关系：两个集合中的元素之间是否有关联。

（2）模糊关系：两个模糊集合中的元素之间关联程度的多少。

3.2.3 模糊关系的合成

3.2.4 模糊推理

3.2.5 模糊决策

模糊决策（模糊判决，解模糊，清晰化）：由模糊推理得到的结论或者操作是一个模糊向量，转化为确定值的过程。

（1）最大隶属度法

（2）加权平均判决法

（3）中位数法

3.1.6 模糊推理的运用

3.2.7 模糊控制系统的组成

与一般的计算机控制系统不同的是，模糊控制系统的控制器是模糊控制器，模糊控制器是基于模糊条件语句描述的语言控制规则，又称为模糊语言控制器。

输入输出变量

（1）模糊控制的输入变量通常取E或E，EC或E，EC，ER，分别构成所谓的一维，二维，三维模糊控制器，一般选择控制量的增量作为模糊控制器的输出变量。

（2）描述模糊控制器的输入，输出变量状态：负大（NB），负中（NM），负小（NS），零（O），正小（PS），正中（PM），正大（PB）。

（3）描述误差变量的词集一般取为：负大（NB），负中（NM），负小（NS），负零（NO），正零（PO），正小（PS），正中（PM），正大（PB）。

模糊变量E的赋值表

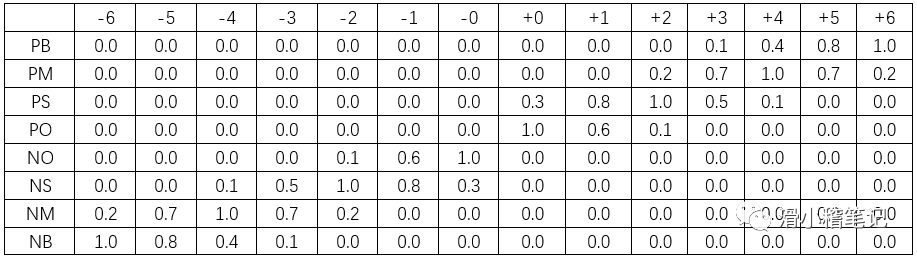
模糊控制规则

（1）条件语句的基本类型为：if A or B and C or D then E

例如水温控制规则之一为：若水温高或偏高，且温度上升快或较快，则加大冷水流量。

用条件语句表达为：if E=NB or NM and EC=NB or NM then U=PB

3.2.8 模糊控制算法的工程实现

在大型的模糊控制系统中常采用软件模糊推理法，模糊关系，模糊推理以及模糊判决的运算可以离线进行，最后得到模糊控制器输入量的量化等级E，EC与输出量即系统控制量的量化等级U之间的确定关系，这种关系通常称为控制表。

3.3 水位控制系统

3.3.1 控制目标

控制模型如下图所示，控制进水阀S1和出水阀S2，使水箱水位保持在目标水位O处。

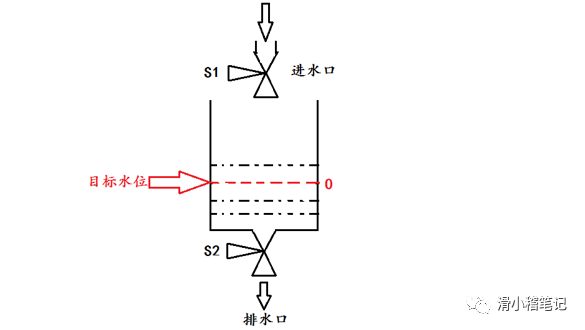
3.3.2 控制规则

（1）若当前水位高于目标水位，则向外排水，差值越大，排水越快

（2）若当前水位低于目标水位，则向内注水，差值越大，注水越快

（3）若当前水位和目标水位相差很小，则保持排水速度和注水速度相等

注：建立模糊控制规则的基本思想：当误差大或较大时，选择控制量应该以尽快消除误差为主，而当误差较小时，选择控制量要防止超调，以系统的稳定性为主要出发点。

3.3.3 控制步骤

（1）我们选择目标水位和当前水位的差值e作为观察量，选取阀门开度u为控制量。

（2）将偏差e划分为5个模糊集，负大（NB）、负小（NS）、零（ZO）、正小（PS）、正大（PB），e为负表示当前水位低于目标水位，e为正表示当前水位高于目标水位。设定e的取值范围为[-3,3]，隶属度函数如下图所示。

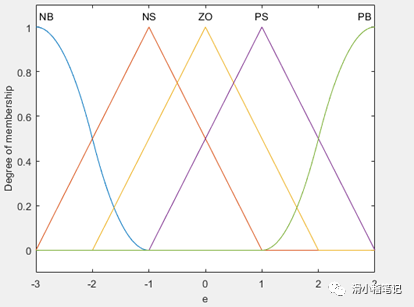
此时偏差e对应的模糊表如下表所示。

	-3	-2	-1	0	1	2	3
PB	0	0	0	0	0	0.5	1
PS	0	0	0	0.5	1	0.5	0
ZO	0	0	0.5	1	0.5	0	0
NS	0	0.5	1	0.5	0	0	0
NB	1	0.5	0	0	0	0	0

（3）将控制量u划分为5个模糊集，负大（NB）、负小（NS）、零（ZO）、正小（PS）、正大（PB），u为负表示增大进水阀门S1的开度（同时减小出水阀门S2的开度），u为正表示减小进水阀门S1的开度（同时增大出水阀门S2的开度）。设定u的取值范围为[-4,4]，隶属度函数如下。

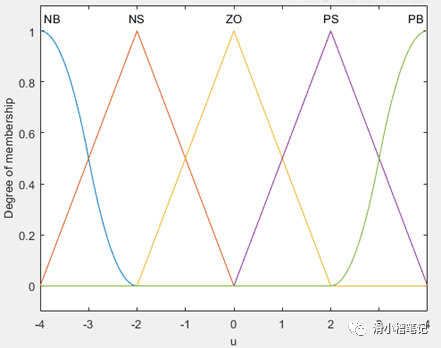
此时控制量u对应的模糊表如下表所示。

	-4	-3	-2	-1	0	1	2	3	4
PB	0	0	0	0	0	0	0	0.5	1
PS	0	0	0	0	0	0.5	1	0.5	0
ZO	0	0	0	0.5	1	0.5	0	0	0
NS	0	0.5	1	0.5	0	0	0	0	0
NB	1	0.5	0	0	0	0	0	0	0

（4）制定模糊规则：模糊规则的制定是模糊控制的核心内容，控制性能的好坏很大程度上由模糊规则决定，目前主要是根据经验来制定相应的规则

若e负大，则u负大

若e负小，则u负小

若e为零，则u为零

若e正小，则u正小

若e正大，则u正大

（6）进行模糊决策：最终需要的控制量u即为模糊控制的输出，u可由偏差矩阵e和模糊关系矩阵R合成得到

（7）控制量的反模糊化

我们模糊决策得到的控制量u是一个矩阵，并不能直接应用在工程上，因此需要将u解释为实际中的特定行为，即反模糊化操作。目前常用的反模糊化方法有以下几种：

最大隶属度法：应用于计算简单控制要求不高场合

重心法：可以使得输出更平滑

加权平均法：工业上应用最广泛

3.4 模糊控制算法实现

3.4.1 MATLAB代码

clc
clear
%创建模糊控制器
a = newfis('fuzzy tank');
%输入变量
a = addvar(a,'input','e',[-3,3]);                           %设置变量e为输入且定义域[-3,3]
a = addmf(a,'input',1,'NB','zmf',[-3,-1]);                  %Z型隶属度函数
a =addmf(a,'input',1,'NS','trimf',[-3,-1,1]);               %三角形隶属度函数
a =addmf(a,'input',1,'ZO','trimf',[-2,0,2]);                %三角形隶属度函数
a =addmf(a,'input',1,'PS','trimf',[-1,1,3]);                %三角形隶属度函数
a = addmf(a,'input',1,'PB','smf',[1,3]);                     %S型隶属度函数
%输出变量
a = addvar(a,'output','u',[-4,4]);                            %设置变量u为输出且定义域[-4,4]
a = addmf(a,'output',1,'NB','zmf',[-4,-2]);                 %Z型隶属度函数
a =addmf(a,'output',1,'NS','trimf',[-4,-2,0]);             %三角形隶属度函数
a =addmf(a,'output',1,'ZO','trimf',[-2,0,2]);               %三角形隶属度函数
a =addmf(a,'output',1,'PS','trimf',[0,2,4]);                %三角形隶属度函数
a = addmf(a,'output',1,'PB','smf',[2,4]);                    %S型隶属度函数
%建立模糊规则
rulelist=[1 1 1 1;
          2 2 1 1;
          3 3 1 1;
          4 4 1 1;
          5 5 1 1];
a = addrule(a,rulelist);
%设置反模糊化算法
a1 = setfis(a,'DefuzzMethod','mom');                         %采用最大隶属度平均法进行反模糊化
writefis(a1,'tank');                                         %保存tank文件
a2 = readfis('tank');                                        %读取tank文件
%绘制图像
figure(1);  plotfis(a2);                                     %绘制模糊控制器结构
figure(2);  plotmf(a,'input',1);                              %绘制输入隶属度函数图像
figure(3);  plotmf(a,'output',1);                             %绘制输出隶属度函数图像
%打开模糊调试器
showrule(a);
ruleview('tank');

MATLAB仿真结果如下图所示。

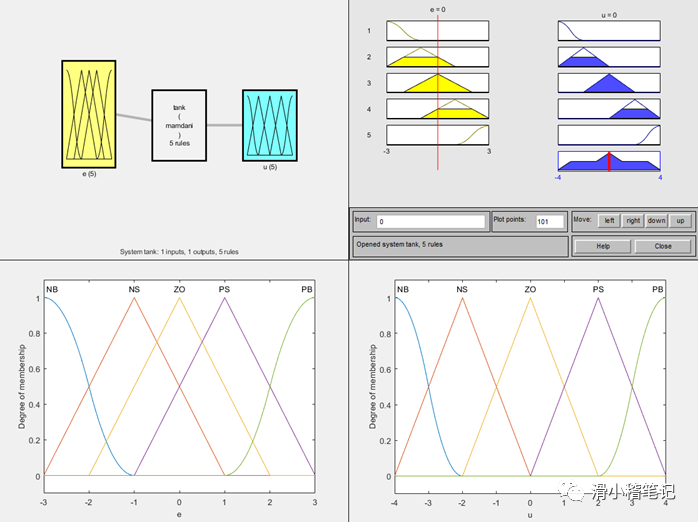
3.4.2 C语言代码

#include 
#include 
#include 
#define  N  7                      //定义量化论域模糊子集的个数
//模糊语言定义
#define  NB  -3
#define  NM  -2
#define  NS  -1
#define  ZO  0
#define  PS  1
#define  PM  2
#define  PB  3
struct
{
  //规则表
  int rule[ N ][ N ] ;                //模糊规则表
  //隶属度函数
  char *f_type_e ;                  //e的隶属度函数类型
  char *f_type_de ;                  //de的隶属度函数类型
  char *f_type_u ;                  //u的隶属度函数类型
  float paras_e[ 3*N ] ;                //e的隶属度函数的参数
  float paras_de[ 3*N ] ;              //de的隶属度函数的参数
  float paras_u[ 3*N ] ;                //u的隶属度函数的参数
  //模糊运算参数
  float Ke ;                    //Ke=n/emax,量化论域为[-3,-2,-1,0,1,2,3]
  float Kde ;                    //Ke=n/demax,量化论域为[-3,-2,-1,0,1,2,3]
  float Ku ;                    //Ke=umax/n,量¢化论域为[-3,-2,-1,0,1,2,3]
  float umax ;                    //输出的上限
  float emax ;                    //误差基本论域上限
  float demax ;                    //误差变化率基本论域的上限
  //控制目标参数
  float target ;                  //控制目标
  float actual ;                  //实际值
  float e ;                    //误差
  float e_pre ;                    //上一次的误差
  float de ;                    //误差的变化率
}_fuzzy_;
/*******************************************************
Name      :trimf
Function    :三角隶属度函数
Parameter  :
      x:自变量
      (a,b,c):定义域
Return    :结果
*******************************************************/
float trimf( float x, float a, float b, float c )
{
  float u ;
  if( ( x>=a )&&( x<=b ) )
    u = ( x-a )/( b-a ) ;
  else if( ( x>b )&&( x<=c ) )
    u = ( c-x )/( c-b ) ;
  else
    u = 0 ;
  return u ;
}
/*******************************************************
Name      :gaussmf
Function    :正态隶属度函数
Parameter  :
      x:自变量
      ave:均值
      sigma:方差
Return    :结果
*******************************************************/
float gaussmf( float x, float ave, float sigma )
{
  float u ;
  if( sigma<0 )
    printf("方差不允许小于0\\n");
  else
    u = exp( -pow( ( ( x-ave )/sigma ), 2 ) ) ;
  return u ;
}
/*******************************************************
Name      :trapmf
Function    :梯形隶属度函数
Parameter  :
      x:自变量
      (a,b,c,d):定义域
Return    :结果
*******************************************************/
float trapmf( float x, float a, float b, float c, float d )
{
  float u ;
  if( ( x>=a )&&( xelse if( ( x>=b )&&( x

**
最终代码运行结果如下图所示。

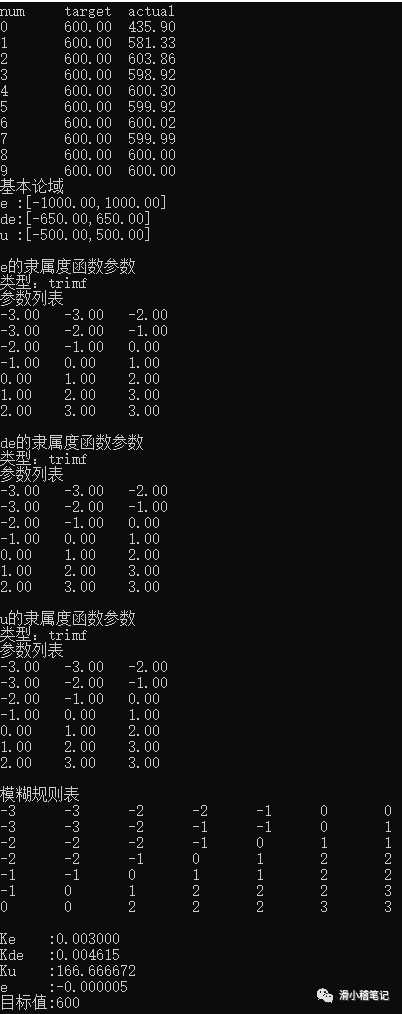
参考于CDSN

**