1、换路定理:换路前后,电容两端的电压不能突变,电感中的电流不能突变,此关系称为换路定则。
2、一阶电路时域分析
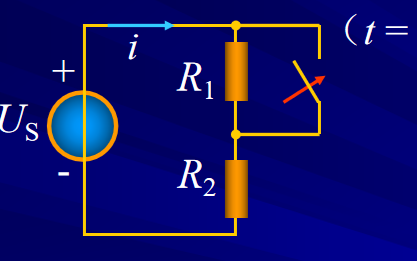
(1)微分方程的建立:电路中存在单个动态元件(一个电容或一个电感)的电路称为一阶电路,常见的一般有一阶RC电路和一阶RL电路。如下图所示
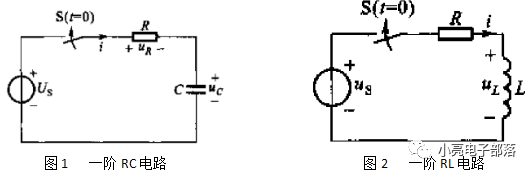
建立微分方程的步骤如下:确定电路中的中间变量(比如电流或电压);通过中间变量确定输入与输出之间的参数方程,消去中间变量即可得到输入与输出之间的方程。
对于一阶RC电路微分方程的建立步骤如下:由于电路是串联,所以取电流i作为中间变量,输入电压为Us,所以根据KVL建立方程
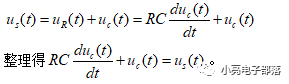
对于一阶RL电路微分方程的建立步骤如下:由于电路是串联,所以取电流i作为中间变量,输入电压为Us,所以根据KVL建立方程
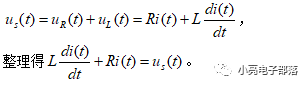
根据换路定理,一般在一阶RL电路中,建立的是电感电流和电压激励的关系,在一阶RC电路中建立的是电压激励和电容电压的关系。
(2) 零输入响应 :所谓零输入响应就是当电路的激励为零的时候,动态元件依靠初始储能完成的输出响应,对应到一阶微分方程上,就是求一阶微分方程的齐次解。对于一阶RC电路,零输入响应为
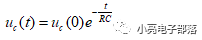
对于一阶RL电路,零输入响应为
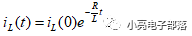
(3) 零状态响应 :所谓零状态响应就是当电路存在输入激励且动态元件的初始状态为0的时候,动态元件依靠输入激励完成的输出响应,对应到一阶微分方程上,就是求一阶微分方程的通解,对于一阶RC电路,零状态响应为
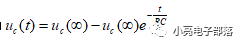
对于一阶RL电路,零状态响应为
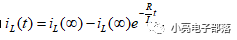
其中无穷代表的是稳态时候的值。
(4)一阶系统的 全响应 :当一个电路的激励和初始状态均不为0的时候产生的响应称为一阶电路的全响应,全响应一般可以拆分为零输入响应和零输出响应的叠加,或者是稳态分量与暂态分量的叠加,所谓暂态分量就是指其幅值随着时间趋向无穷大而趋向于0的部分。所以一阶电路的全响应的求解可以采用三要素法,其中的三要素就是稳态值,初始值和时间常数,即全响应
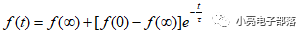
其中对于一阶RC电路来说时间常数等于RC;对于一阶RL电路来说时间常数等于L除以R。
3、二阶电路时域分析
(1)微分方程的建立:二阶系统即电路中同时存在两个动态元件,一般是电容和电感同时存在,此时建立的方程是一个二阶常系数非齐次线性微分方程,这种方程的求解通常比较复杂,因此不要求掌握,理解即可。方程的建立方式与一阶系统一样。
(2)零输入响应
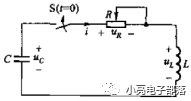
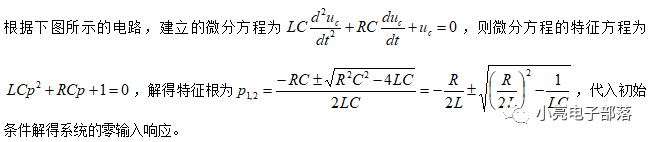
(3)零状态响应与全响应:二阶系统的零状态响应与全响应只需要求解对应的微分方程通解即可,本部分不再赘述。
3、阶跃响应与冲激响应:当输入为阶跃信号与冲激信号时系统产生的响应称为阶跃响应与冲激响应。由于一阶系统和二阶系统一般为LTI系统(线性时不变连续系统),所以满足线性性质,微分性质和积分性质。


5、例题分析
例题1:已知图中开关在位置1处很久,当t=0时刻转换到位置2,求换路后的电感的电流和电感两端的电压。
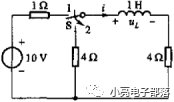

例题2:已知图中开关在位置1处很久,当t=0时刻转换到位置2,求换路后的100K电阻上的电流和电容两端电压。
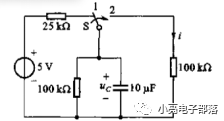

例题3:已知微分方程为
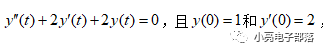
求解系统的零输入响应。

例题4:计算
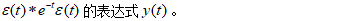
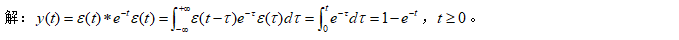
-
电路
+关注
关注
173文章
5989浏览量
173478 -
RC电路
+关注
关注
2文章
164浏览量
30448 -
RL电路
+关注
关注
0文章
7浏览量
6207
发布评论请先 登录
相关推荐
第7章 一阶电路和二阶电路的时域分析
第7章 一阶电路和二阶电路的时域分析
二阶有源低通滤波器_最简单的二阶低通滤波器电路图
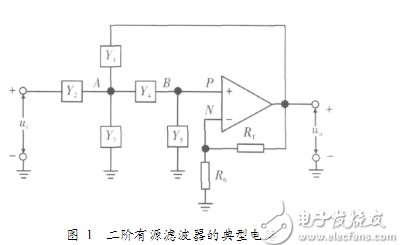




 一阶电路与二阶电路的时域分析
一阶电路与二阶电路的时域分析
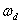











评论