采用低成本微控制器的高性能计算

微控制器 （μC） 比以往任何时候都更具有类似 DSP 的功能，以及更传统的 ALU 内核。遗憾的是，许多不熟悉DSP算法和编码技术的固件开发人员未能充分利用这些设备提供的功能。本文是固件开发人员在低成本μC中使用信号处理技术的入门书。

微控制器角色的转变

不久前，使用μC进行设计意味着CPU本身周围有大量的外设和支持芯片。即使CPU有足够的嵌入式ROM和RAM，任何重要的项目都需要外部支持芯片提供的功能。当系统涉及任何类型的模拟信号时，这一点从未如此真实。即使是最简单的模拟信号要求，系统复杂性也会膨胀。但是，这就是问题所在——声音、温度、压力和其他自然现象的现实世界仍然是模拟的。实际上，能够在模拟世界中运行的系统需要：

传感器和模拟模拟信号调理器，用于将物理现象转换为电信号

数据采集子系统至少由具有足够精度和速度的模数转换器（ADC）和数模转换器（DAC）组成

能够处理采样数据的数字信号处理器 （DSP）

具有足够吞吐量的μC来管理DSP、数据采集子系统和其他外设，并具有足够的剩余带宽以平稳执行控制和用户界面功能;μC还可能包含程序ROM和数据RAM

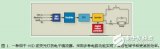
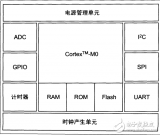
这些复杂的设备提高了最终产品的成本，使其价格超出了低端应用的范围。然而，一类新的μC已经出现，它通过在同一芯片上嵌入高性能数据采集子系统、类似DSP的功能和RISC CPU内核来简化与模拟世界的接口。现代μC的集成示意图如图1所示。

新一代μC的一个例子是MAXQ3120。除了常用的UART、定时器和I/O端口阵列外，MAXQ3120还集成了一组外设，使模拟接口变得简单：

16 位、1 周期 RISC 内核

一对 16 位、Σ-Δ ADC

能够在PWM模式下工作的16位定时器

带 16 位累加器的 16 x 40 乘法器

MAXQ3120还包括一个时间时钟、一个LCD控制器和硬件，以方便与IR通信通道接口。在下面的例子中，周期计数或存储要求将特指MAXQ3120 μC。

现代μC在器件内集成了大多数必要的系统功能，包括模拟外设和MAC。

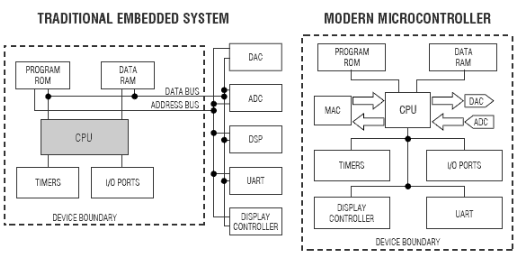
图1.传统的嵌入式系统必须公开地址和数据总线，以便连接外部I/O设备以完成系统。

思考问题

涉及信号处理的问题最好分三个阶段解决：

你想做什么？仔细剖析问题并将其分解为尽可能小的功能单元。问题是否涉及滤波、信号辨别或特定类型信号的生成？将问题划分为一系列更简单的子任务后，即可进行下一步。

你是怎么做到的？现在搜索文献、网络或其他资源，找到与每项任务相关的算法。您可能会发现您的大多数概念问题已经解决。您所要做的就是最后一步。

编码它。将算法转换为代码的任务是熟悉的任务，可用的硬件资源使其比以往任何时候都更容易。

在下面的示例中，我们坚持三个步骤：描述问题，呈现算法和方法，并提供解决问题的代码示例。

功率监控和测量示例 模拟至μC接口的一个常见示例
是测量交流电路的电压和电流，以确定负载消耗的功率。乍一看，这似乎相对简单——如果电压和电流波形是正弦的，则RMS电压和电流仅为峰值电压或电流的1/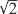倍。将RMS电压和电流相乘，结果就是以瓦特为单位的功率。还有什么比这更简单的呢？

这种分析有两个问题。首先，虽然电力公司提供的电压通常非常接近正弦，但电流波形不是。灯调光器、开关电源和荧光灯都为电源线提供非正弦电流曲线。简单地乘以常数不会得到 RMS 电流值。其次，即使电流波形是正弦的，除非电压和电流波形精确地同相，否则简单地乘以RMS值并不能提供以瓦特为单位的实际功率使用情况。通常，实际负载包含容性电抗，或者更常见的是感抗。因此，必须考虑无功功率。我们必须回到根本，找到更好的方法。

在每个时刻，瞬时电压和电流的乘积就是瞬时功率。图2显示了这种瞬时功率如何上升和下降，甚至可能在部分周期内降至零以下，具体取决于电流。总有功功率只是瞬时电压和瞬时电流乘积的时间平均值。找到实际功率很简单——将电压样本和电流样本相乘，然后将结果添加到累加器中。累积足够数量的样本后，只需将总和除以样本数即可获得以瓦特为单位的功率。要将其转换为以瓦特秒为单位的能量，请乘以样本累积的时间（以秒为单位）。

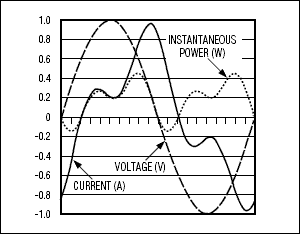
图2.虽然电压波形（虚线）通常非常接近正弦，但电流波形（实线）可能与纯正弦波形有很大差异。此外，电流波形可能会同相偏移，导致线路周期某些部分的瞬时功率（虚线）变为负值。

无功功率的计算并不那么简单。首先，请注意，对于正弦电压和电流，无功功率定义为：

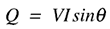
其中V是RMS电压，I是RMS电流，

是电流和电压波形之间的相位差。

电抗元件产生的功率可以随时通过计算差值来确定：

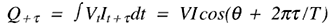
和

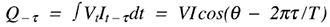
其中 Vt和我t是任何时间电压和电流的瞬时值，是任意延迟，

T是一个线路周期的周期。区别在于：

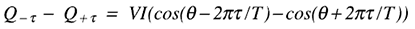
使用三角恒等式 cos（A+B） = cosAcosB - sinAsinB 和 cos（A-B） = cosAcosB + sinAsinB 将等式更改为：

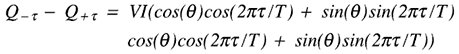
请注意，余弦项取消，正弦项加强，仅保留：

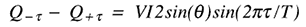
但是 VI sin（

） 是 Q，这就是我们试图找到的。因此，重新排列术语会留下：

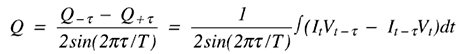
这意味着无功功率可以通过累加最近电流样本与先前电压样本以及最新电压样本与上一个电流样本之差的差值来计算。如果设置为采样周期，则上述公式中的分母是一个常数，

因此可以预先计算。

一旦知道有功功率和无功功率，视在功率（如果将RMS电压和功率相乘时将计算出的功率）可以很容易地计算为：

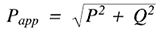
最后，通过将实际功率除以视在功率来求出功率因数。

假设目前需要跟踪所有这些因素，应用将需要跟踪电压通道和电流通道的乘积之和，以及前面关于无功功率的讨论中描述的乘积差异的总和。累积实际权力的代码如下所示：

void accumulateRealPower(int i_sample, int
v_sample)
{
static long real_power;
initMAC(MULTIPLY_ADD);
preloadMAC(real_power);
real_power = getMAC(v_sample,
i_sample);
}

在此示例中，该函数采用一个字节，用于在 MAC 中设置操作参数。该函数在乘法运算之前将长变量加载到累加器中。

initMACpreloadMAC

为了演示如何将其转换为实际的机器指令，请考虑以下基于上述代码的操作集：

初始化乘法累加单元或 MAC（一个周期）

设置内存指针以对存储区域求和（一个周期）

将旧总和加载到累加器中（两个周期）

将电压样本加载到乘法器中（一个周期）

将当前样本加载到乘法器中（一个周期）

等待一个周期以完成累积操作（一个周期）

将累加器保存到内存（一个周期）

因此，需要八个周期来积累实际功率。累积无功功率类似：

请注意，本讨论假设输入样本的直流偏移为零。如果不是这样，则需要为电压和电流通道本身提供额外的累加器。如果直流偏移为零，则这些总和将为零。否则，必须从累积的实际功率中减去直流失调所代表的功率。

void accumulateReactivePower(int i_sample, int
v_sample)
{
static long reactive_power;
initMAC(MULTIPLY_ADD);
preloadMAC(reactive_power);
reactive_power = getMAC(prev_v_sample,
i_sample);
initMAC(MULTIPLY_SUB);
reactive_power = getMAC(prev_i_sample,
v_sample);
}

过滤示例
过滤是数字领域最常见的任务之一。原因很简单——理想滤波器在模拟世界中无法实现，但在数字逻辑中实现起来相对简单。

本节将介绍低通滤波器和带通滤波器。低通滤波器通常用于在采样之前从信号中去除不需要的高频分量，以消除混叠伪影。带通滤波器通常用于将通信信道限制在特定的频率范围内。例如，FSK调制解调器可以使用带通滤波器来消除高频和低频噪声分量，只留下感兴趣的频率进行处理。

关于数字滤波器主题的文章已经写了很多，可能使人们认为这个主题很难理解。实际上，基础知识很简单，无需成为DSP专家即可使用滤波功能。

通过检查图3中的低通滤波器图，可以看出：

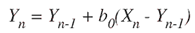
其中 Yn是当前输出样本 YN-1是 以前的输出样本和 Xn是当前输入 样本。滤波器常数，b0，预先计算为：

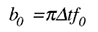
其中 f0是所需的半幅度转折频率，并且

是采样周期。因此，对于 8kHz 的采样速率和 100Hz 的所需转折频率，b0等于 p x 125μs x 100Hz = 3.93 x 10-2

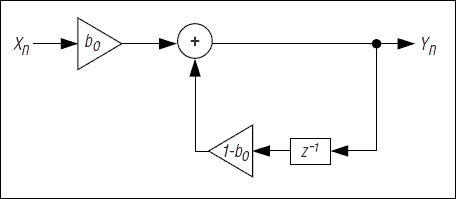
图3.在发出信号之前，使用单极点低通滤波器从信号中去除不需要的高频分量。

实现过滤算法非常简单：

long lpf(int input_sample) { static long prev_out; initMAC(MULTIPLY_SUB); preloadMAC(prev_out); prev_out = getMAC(b0, prev_out); initMAC(MULTIPLY_ADD | ONE_OP); prev_out = oneopMAC(input_sample); return prev_out; }

该函数仅将一个操作数加载到乘数中，期望乘数保持第二个操作数。这样做是为了节省执行时间。该过滤器如果有效编译，每个样本只需要十个周期。时钟为8MHz时，一阶低通滤波器仅消耗MAXQ1处理带宽的1%左右（不考虑中断开销）。

oneopMAC

二阶带通滤波器在概念上要复杂一些，尽管实际上很相似，只增加了算法的几个步骤。一个简单的二阶带通滤波器的信号流图如图2所示，其公式为：

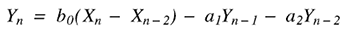
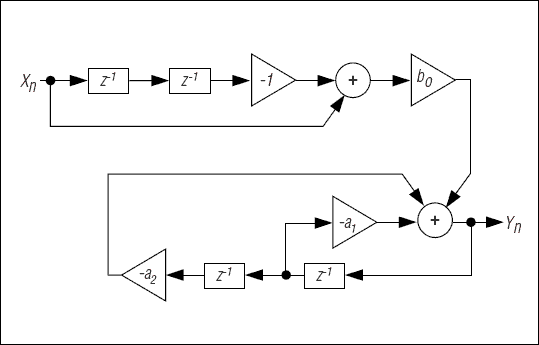
图4.二阶带通滤波器可以将通信信道限制在特定的频率范围内。

与前面的示例一样，参数 b0一个1，以及2是预先计算的。该 a1参数定义滤波器的Q因子，即滤波器抑制中心频率附近带外频率的效率的度量。具体说来

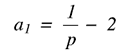
p 通常在 100 到 1，000 的范围内。p值越大，表示通带越窄，但滤波器建立时间越长。p值越小，通带越宽，建立时间越短。

其他参数，a2和 b0，按1.首先，我们定义两个中间变量：

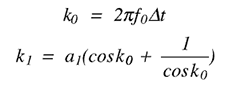
现在我们可以定义其他两个参数：

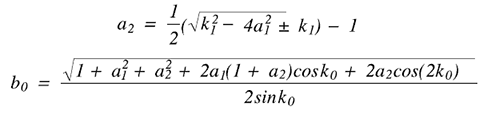
请注意，一旦选择了中心频率、采样率和滤波器Q因子，参数就是常数。必要的代码是：

long bpf(int input_sample)
{
static long x[1], y[1], output;
initMAC(MULTIPLY_ADD | CLEAR_ACC);
output = getMAC(y[1], a2);
initMAC(MULTIPLY_SUB);
}

output = getMAC(y[0], a1);
output = getMAC(x[1], b0);
initMAC(MULTIPLY_ADD | ONE_OP);
output = oneopMAC(input_sample);
x[1] = x[0];
x[0] = input_sample;
y[1] = y[0];
y[0] = output;
return output;
}

如果有效编译，此例程（不包括输入和输出样本的老化）需要十四个周期。老化不包括在周期估计中，因为样品通常存储在循环缓冲液中，不需要老化。

音调生成和检测示例
在通信应用中，通常需要生成/检测音频通道中的音调组合。例如，在电话应用中，想要在电话线路中合成或检测双音多频音（DTMF）以在电话线上拨号的情况并不少见。在中继卡中，标准多频 （MF） 音通常用于带内信令。呼叫进度信令（拨号音、回铃、忙音和重新排序等）通常表示为两个或多个音调的组合。

双极数字谐振器（图5）是生成音调的简单方法。谐振器的公式为：

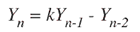
其中 k 是：

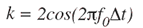
并且可以预先计算。请注意，该谐振器没有输入 - 它连续运行而无需干预。然而，要启动谐振器，YN-1必须设置为零和 YN-2设置为 -Asink，其中 A 是所需的信号幅度。

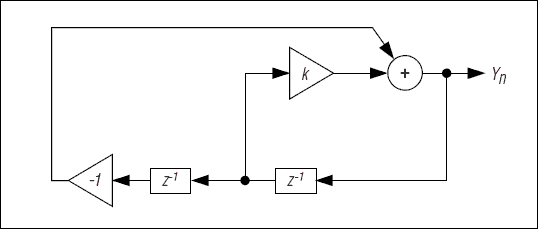
图5.双极数字谐振器用于产生正弦波。

产生正弦波的算法是迄今为止提出的最简单的算法：

long gen_tone_sample()
{
static long y[1];
initMAC(MULTIPLY_ADD);
preloadMAC(-y[1]);
y[1] = y[0];
y[0] = getMAC(y[0], k);
return y[0];
}

此例程的代码大小估计值为每个要生成的正弦波样本大约八个机器周期。这具有类似于产生简单方波的CPU强度，然后必须通过外部模拟电路对其进行滤波，以产生许多应用所需的频谱纯度。

音调检测稍微复杂一些，尽管在削减基本要素时并不那么令人生畏。为了检测音频通道中的音调，我们选择 Goertzel 算法。该算法利用二阶滤波器和功率测量公式来确定滤波器通带中是否存在能量。

图 2 中二阶滤波器的公式为：

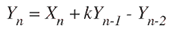
其中 k 的定义与前面描述的音调生成器中的定义相同。算法为：

long *tone_filter(int input_sample)
{
static long y[1], output;
initMAC(MULTIPLY_ADD);
preloadMAC(-y[1]);
y[1] = y[0];
y[0] = getMAC(y[0], k) +
input_sample;
return y;
}

请注意，此例程返回数组而不是标量值。这是因为下一步需要最新结果和上一个结果。一个音调检测器通道的周期计数估计为 12 个周期，或者在 8kHz 采样速率下，约为 CPU 马力的 1.5%。通常，在滤波器稳定并提供音调存在的可靠指示之前，它需要 100 多个采样周期。

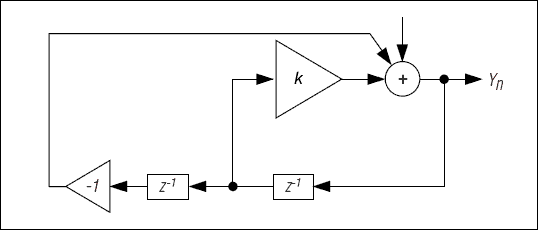
图6.音调检测可以通过二阶滤波器执行。

为了测试是否存在音调，有必要计算滤波信号中的功率。这可以使用以下等式完成：

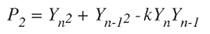
由于系数与滤波器环路预先计算的系数相同，因此我们可以在此处使用它来计算功率：

power_squared = y[0] * y[0] +
                y[1] * y[1] -
                k * y[0] * y[1];

在足够数量的采样周期后，音调存在由平方功率指示显示，在没有音调的情况下，该指示将至少比测量值高一个数量级。在测试中，音调的存在可能表明输入处的单位信号幅度大于 1，000 的平方幅度。非频率音或非频率音的组合通常显示小于 50 的平方振幅。

结论

随着数据采集硬件和类似DSP的构建模块在廉价μC上变得越来越普遍，固件工程师必须找到将DSP功能引入主CPU的方法，以降低成本并提高性能。然而，凭借文献和网络上的丰富资源，这项任务比预期的要容易得多。

审核编辑：郭婷