系统和设计工程师通常使用噪声系数来确保最佳信号性能。然而,在信号链中使用混频器会给简单的噪声系数分析带来挑战。本教程首先检查噪声系数的基本定义,然后对涉及混频器的级联模块进行基于方程的分析,然后是测量噪声系数的典型实验室技术。本教程还介绍了噪声温度和Y因子噪声测量的概念,然后探讨了使用Y因子方法进行混频器噪声系数测量。讨论了双边带(DSB)和单边带(SSB)噪声系数测量的示例。
介绍
噪声系数的一般概念已被系统和电路设计人员很好地理解和广泛使用。特别是,它用于传达产品定义人员和电路设计人员的噪声性能要求,并预测接收器系统的整体灵敏度。
当混频器是信号链的一部分时,噪声系数分析的主要困难就出现了。所有实际混频器都围绕本振(LO)频率折叠RF频谱,从而创建一个输出,其中包含根据f外= |f射频, G瞧|.在外差架构中,其中一个贡献通常被认为是虚假的,另一个是有意的。因此,可能会采用图像拒绝过滤或图像消除方案来在很大程度上消除这些响应之一。在直接变频接收器中,情况有所不同;两个边带(高于和低于 F射频= f瞧) 被转换并用于所需信号。因此,这确实是混频器的双边带(DSB)应用。
工业中常用的各种定义在不同程度上解释了噪声折叠。例如,传统的单边带噪声因数F单边 带,假设允许来自两个边带的噪声折叠到输出信号中。但是,只有一个边带可用于传达所需信号。这自然会导致噪声系数增加3dB,假设两个响应的转换增益相等。相反,DSB噪声系数假设混频器的两个响应都包含所需信号的一部分,因此噪声折叠(以及相应的信号折叠)不会影响噪声系数。DSB噪声系数适用于直接变频接收器以及射电天文接收器。然而,更深入的分析表明,设计人员仅仅为给定应用选择正确的噪声系数“风味”,然后在标准弗里斯方程中替换相应的数字是不够的。这样做可能会导致严重的错误分析,当混频器或混频器后面的组件在确定系统噪声系数方面起着不可忽视的作用时,这种情况可能特别严重。
本教程将噪声系数的基本定义、涉及混频器的级联模块的基于方程的分析以及测量噪声系数的典型实验室技术结合在一起。在其中,我们展示了级联噪声系数方程如何通过一个或多个混频器的存在进行修改,并推导出许多流行的下变频架构的适用方程。然后,我们描述了噪声系数测量的Y因子方法,使用混频器作为被测器件(DUT)。使用混频器作为DUT可以确定适当的混频器噪声系数测量方法,这些方法可以有效地应用于级联方程。
混频器噪声的概念模型
可视化混频器噪声贡献的一种方法是考虑混频器的概念模型(图 1)。该模型基于安捷伦 Genesys 仿真程序提供的模型。1
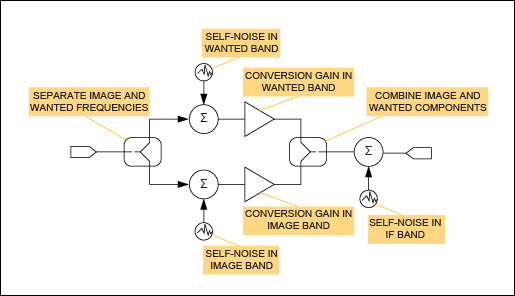
图1.混频器噪声贡献。
在该模型中,输入信号被分成两个独立的信号路径,一个表示高于LO的RF频率,另一个表示低于LO的频率。每条路径都受到混频器中独立的加性噪声处理,并施加独立的转换增益。最后,将两条路径转换为IF频率,并与混频器输出级中可能产生的进一步噪声贡献相加。每单位带宽的自噪声功率在所需波段和镜像波段中可能不同;相应的转换增益也可能不同。
为方便起见,我们可以将所有噪声源引用到输出,并将它们收集到全局噪声项 N一个,表示混频器输出端口每单位带宽的总额外噪声功率。
N一个= NSGS+ N我G我+ N如果
请注意,N一个完全不依赖于混频器输入端口是否存在信号。
总结了混频器的内部噪声源后,我们现在转向源端接引起的噪声(图2)。我们确定了两个离散噪声源,分别代表由于源端接在所需频率和镜像频率下的输入噪声密度。我们必须将这些视为独立的量,因为应用电路可能导致其中一个衰减,而另一个以低损耗传输到混频器的RF输入端口。如果图像和所需的RF频率很好地分离并且采用频率选择性匹配,则可能会出现这种情况。
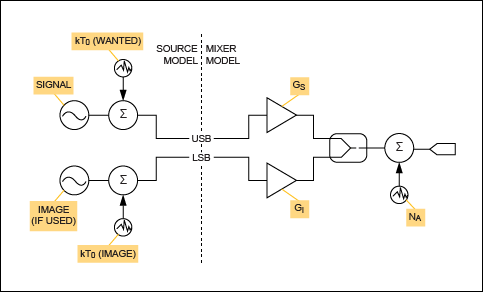
图2.源噪声和混频器噪声贡献。
在宽带匹配的情况下,我们可以写 N外= N一个+ 千吨0GS+ 千吨0G我.但是,在所需RF频率下与混频器进行高Q值频率选择性匹配的情况下,由于源端接在镜像频率处,输出端的噪声可能可以忽略不计,导致N外= N一个+ 千吨0GS.通常,我们可以为混频器输入端口在镜像频率下可用的输入源端终端噪声功率的有效比例分配一个系数α。因此,N外= N一个+ 千吨0GS + αkT0G我,其中 α 是 0 ≤ α ≤ 1 范围内的特定于应用的系数。稍后我们将看到应用中的有效噪声系数取决于α的值。
噪声系数定义
在讨论为什么级联噪声系数计算会产生误导之前,我们应该回顾一下该术语的一些基本定义。
解释双端口网络的噪声因数 (F) 的合理起点是:
F = (SNRIN)/(SNROUT)
当以dB表示时,称为噪声系数(NF):
NF = 10log10(F)
此表达式取决于输入信号的信噪比。然而,如果未定义SNR,则该度量作为电路或组件本身的性能度量毫无意义,因为它在很大程度上取决于馈送信号的质量。因此,最好假设输入端的SNR处于最佳情况,即唯一的噪声源是由于输入端接在某个定义温度下的热噪声引起的。假设噪声因数不依赖于所使用的信号电平也是合乎逻辑的。这假定所表征的双端口网络位于其线性工作区域中。如果我们让输入信号功率为 P 可以看出这一点在信号增益为Gs.然后,输出功率由P外= GsP在和:
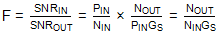
此外,这些噪声功率,N在和 N外,定义不明确,除非我们指定测量它们的带宽。这可以通过指定 N 来解决在和 N外表示任何给定指定输入和输出频率下每单位带宽的噪声功率。
单边带噪声因数
上述考虑因素有助于解释IEEE噪声因子定义的基本原理:
噪声系数(噪声系数)(双端口传感器)。在指定的输入频率下)输出端口可用相应输出频率下每单位带宽的总噪声功率与2)在标准噪声温度(1K)下由输入端接在输入频率处产生的那部分290)之比。
注1:对于外差系统,原则上将有多个输出频率对应于单个输入频率,反之亦然;对于每对相应的频率,定义一个噪声因子。
注2:短语“在输出端口可用”可以替换为“由系统传送到输出端接”。
注3:仅当指定了输入端接时,通过噪声因子来表征系统才有意义。
噪声因数的这个定义是输出频率的点函数,相对于一个相应的RF频率,而不是同时对RF频率,这就是使其成为单边带(SSB)噪声因数的原因(见图3)。
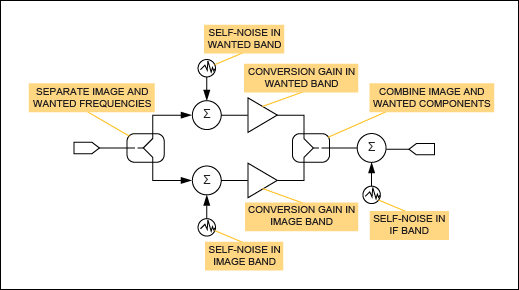
图3.SSB 噪声系数。
需要注意的是,分母仅包括来自一个边带的噪声;分子包括相应输出频率下每单位带宽的总噪声功率,而不进行任何特定排除。为了在具有信号和图像响应的混频器的情况下以数学形式明确这一点,上述定义可以写成:
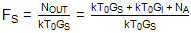
其中 G我是镜像频率下的转换增益;GS是信号频率处的转换增益;T0是标准噪声温度;和 N一个是在输出端子测量的混频器电子元件增加的每单位带宽的噪声功率。镜像频率对应的噪声因子可以写成:
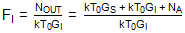
如果镜像频率处的转换增益与所需信号频率处的转换增益不同,则此数字不同。有些人将上述IEEE定义解释为将图像噪声从术语“输出端口可用的相应输出频率下每单位带宽的总噪声功率”中排除。3因此,他们假设:
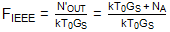
该定义对应于镜像频率处的源输入噪声完全从混频器的输入端口中排除的情况。这种解释并未被行业从业者广泛使用。不过,为了完整起见,如图 4 所示。
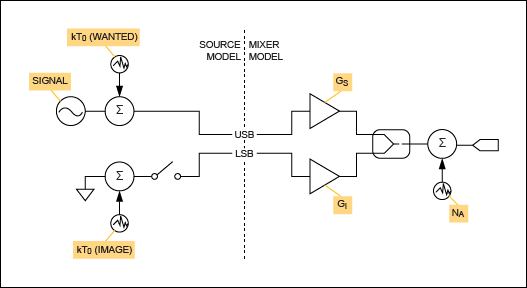
图4.SSB噪声系数的IEEE变体。
美国联邦标准 1037C 对噪声因数有以下定义:
噪声系数:在标准噪声温度(通常为290K)下,器件的输出噪声功率与输入端接中可归因于热噪声的部分之比。注意:因此,噪声系数是实际输出噪声与设备本身不引入噪声时剩余噪声的比率。在外差系统中,输出噪声功率包括镜像频率变换的杂散贡献,但在标准噪声温度下,输入端接中可归因于热噪声的部分仅包括通过系统主频率变换出现在输出中的部分,不包括通过镜像频率变换出现的部分。同义词噪声因子。
由于这个较新的定义明确包括输出噪声功率中镜像频率变换的杂散贡献,因此SSB噪声因数可以按照前面的建议编写:
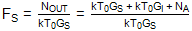
让我们考虑 G 的情况S= G我.然后:
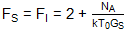
如果我们进一步考虑混音器本身不增加噪声的情况,N一个= 0,那么我们剩下 F = 2 或 NF = 3.01dB。这与无噪声混频器的SSB噪声系数为3dB的说法相对应。
双边带噪声因数
在某些情况下,“系统原理变频”不是适用的术语;这两种反应同样需要和有用。示例包括辐射计和直接变频接收器。在直接变频接收器中,LO频率位于所需信号的RF通带的中心;混频器的两个响应构成整个所需信号频谱的连续一半。图 5 说明了这种情况。

图5.DSB 噪声系数。
因此,在这种情况下,考虑DSB噪声因子是有意义的:
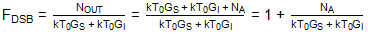
如果我们假设 Gs= G我然后:
FDSB= 1 + (N一个/(2kT0GS))
在相同的约束下:
FSSB = 2 + NA/(kT0GS)
因此,在两个转换增益相等的情况下,混频器的SSB噪声系数比相应的DSB噪声系数高3dB。此外,如果混频器不增加任何额外的噪声(N一个= 0),则 FDSB= 1 或 NFDSB= 0分贝。
噪声系数在级联噪声系数计算中的应用
基线案例:线性电路块级联
考虑以下三个放大器模块的简单级联(图 6)。
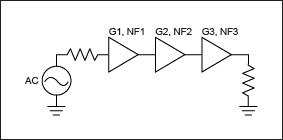
图6.三个增益模块级联。
输出端的总噪声可计算如下:
NOUT = kT0G1G2G3 + NA1 G2G3 + NA2G3 + NA3
由级联输入端的热噪声引起的输出端噪声为:
NOT = kT0G1G2G3
这意味着整体噪声因子为:
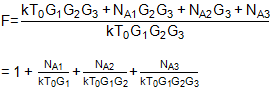
代:
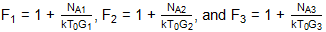
收益 率:
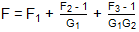
这可以被认为是三个块的标准弗里斯级联噪声方程。从这里扩展到任意数量的块是微不足道的。
外差转换级
考虑接收器信号路径中的以下频率转换级(图 7)。混频器的DSB噪声系数为3dB,转换增益为10dB。所需载波频率为2000MHz,LO选择为1998MHz,因此所需频率和镜像频率都在滤波器的通带内。
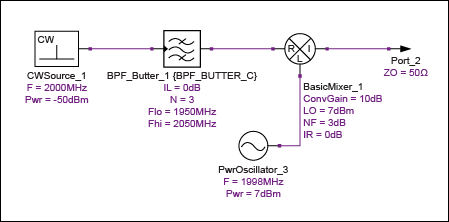
图7.无镜像抑制的外差级。
表1总结了这种布置的级联性能,其中CF是信道频率,CNP是信道噪声功率(以1MHz带宽测量),增益是级增益,CG是级联增益,包括当前级,CNF是级联噪声系数。
| 部件 | CF (兆赫) | 压缩液 (分贝) | 增益(分贝) | CG (分贝) | 碳氢氟 (分贝) |
| CWSource_1 | 2000 | -113.975 | 0 | 0 | 0 |
| BPF_Butter_1 | 2000 | -113.975 | -7.12E-04 | -7.12E-04 | 6.95E-04 |
| BasicMixer_1 | 2 | -97.965 | 10 | 9.999 | 6.011 |
| *滤镜无图像抑制。 | |||||
这两个模块的总级联增益为9.999dB,而SSB噪声系数为6.011dB。从前面的分析中可以正确预测到该噪声系数,因为我们预计SSB噪声系数比混频器的DSB系数高3.01dB。由于滤波器的有限插入损耗,噪声系数还会下降。总体而言,这一结果符合我们的预期。
现在我们考虑相同的情况,但LO频率恢复到1750MHz(图8)。在此LO频率值下,镜像为1500MHz,远远超出混频器前面滤波器的通带。
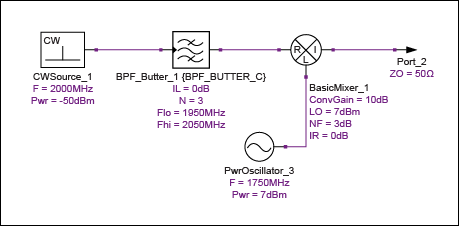
图8.具有镜像抑制功能的外差级。
表2总结了这种安排的级联性能。所需信号的增益与以前相同,但级联噪声系数(CNF)已更改为4.758dB的值。
| 部件 | CF (兆赫) | 压缩液 (分贝) | 增益(分贝) | CG (分贝) | 碳氢氟 (分贝) |
| CWSource_1 | 2000 | -113.975 | 0 | 0 | 0 |
| BPF_Butter_1 | 2000 | -113.975 | -7.12E-04 | -7.12E-04 | 6.95E-04 |
| BasicMixer_1 | 250 | -99.218 | 10 | 9.999 | 4.758 |
| *滤镜的显著图像抑制。 | |||||
为了解释这一结果,我们需要考虑这种情况下的噪声情况与图4所示的情况相似。具体而言,源阻抗镜像噪声被抑制。混频器级增加的噪声可以通过先前推导的DSB噪声因子公式计算得出:
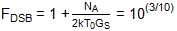
因此:
NA = 2kT0GS(10(3/10) - 1)
现在混频器输出端的总噪声由N给出外= N一个+ 千吨0GS + αkT0G我,在此应用程序中为 α = 0。因此:
NOUT = 2kT0GS(10(3/10) - 1) + kT0GS
得到的噪声系数可以写成:
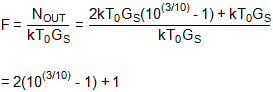
以dB表示,我们有:
NF = 10log10(2(10(3/10)- 1) + 1) = 4.757dB
这应该与4.758dB的仿真值进行比较,其中包括滤波器插入损耗的微小额外贡献。
通常,混频器级的有效SSB噪声系数由下式给出:
FSSBe= 2(FDSB– 1) + 1 + α
其中a = 0表示镜像频率处的端接噪声得到良好抑制的情况,α = 1表示完全没有抑制的情况。请注意,如果α = 1,则有效单边带(SSB)噪声系数降至FSSBe= 2楼DSB,这是本节开头说明的情况。在某些情况下,可能会出现分数值,例如,如果镜像抑制滤波器不直接耦合到混频器输入端子,或者图像和所需响应之间的频率间隔不大。
外差接收器
通过图9中的示例,我们可以看到如何在更大的级联分析中应用有效噪声系数。为了计算整个链的级联噪声系数,我们需要将混频器及其相关的LO和镜像抑制滤波封装为具有特定增益和噪声系数的等效双端口网络。该双端口网络的有效噪声因数为 FSSBe= 2(FDSB– 1) + 1,因为镜像频率处的端接噪声被前置滤波器很好地抑制了。
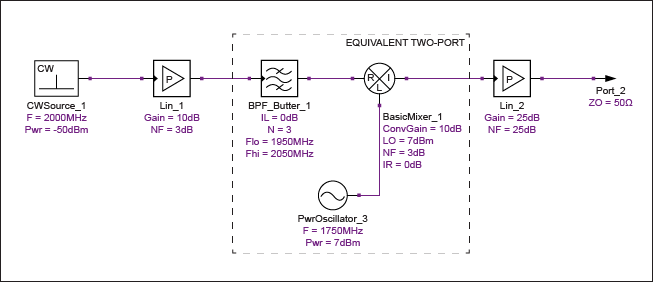
图9.相邻系统模块环境中的外差混频器。
请注意,适用的噪声系数既不是混频器的DSB,也不是SSB噪声系数。相反,它是一个介于这两个值之间的有效噪声数字。在这种情况下,DSB噪声系数为3dB,双端口网络的等效噪声系数可以计算为4.757dB,如上所述。在整个级联计算中使用该值得出的系统噪声系数为7.281dB,如表3所示。手动计算表明,该结果与使用4.757dB作为混频器噪声系数的标准弗里斯方程一致。
| 部件 | CF (兆赫) | 压缩液 (分贝) | 增益(分贝) | 信噪比 (分贝) | CG (分贝) | 碳氢氟 (分贝) |
| CWSource_1 | 2000 | -113.975 | 0 | 0 | 0 | 0 |
| Lin_1 | 2000 | -100.975 | 10 | 3 | 10 | 3 |
| BPF_Butter_1 | 2000 | -100.976 | -7.12E-04 | 7.12E-04 | 9.999 | 3 |
| BasicMixer_1 | 250 | -90.563 | 10 | 3 | 19.999 | 3.413 |
| Lin_2 | 250 | -61.695 | 25 | 25 | 44.999 | 7.281 |
通常,当用等效的双端口网络代替混频器及其相邻组件时,输入端口应该是信号流中镜像响应被拒绝的最新节点。输出端口应该是图像和所需响应组合在一起的最早节点(通常是混音器的输出端口)。如果混频器的图像响应没有被架构有效抑制,那么弗里斯方程就不能不修改地使用。
零中频接收器
现在考虑零中频(ZIF)或直接变频接收器(图10)。
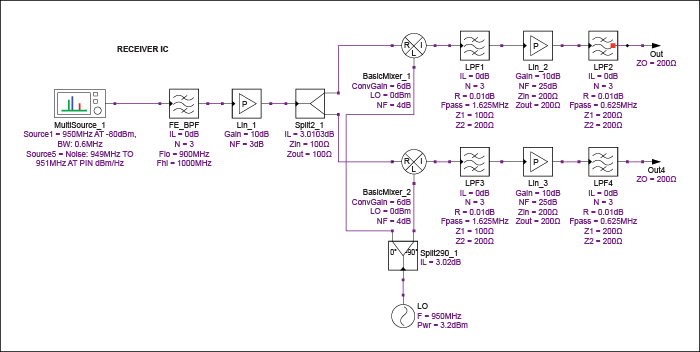
图 10.带有低噪声放大器 (LNA)、混频器、滤波器和可变增益放大器 (VGA) 的 ZIF 接收器。
该系列包括一个具有10dB增益和3dB噪声系数的LNA;以950MHz为中心的带通滤波器;信号分配器,用于将信号发送到一对混频器,每个混频器的转换增益为6dB;DSB噪声系数为4dB。VGA的定义增益为10dB,噪声系数为25dB。对该阵容的仿真产生了表4所示的结果,其中CP是通道功率,SNF是级噪声系数。其他项目与前面的表相同。
| 部件 | CF (兆赫) | CP (分贝) | 压缩液 (分贝) | 增益(分贝) | 信噪比 (分贝) | CG (分贝) | 碳氢氟 (分贝) |
| MultiSource_1 | 950 | -79.999 | -116.194 | 0 | 0 | 0 | 0 |
| FE_BPF | 950 | -80.009 | -116.194 | -9.99E-03 | 1.00E-02 | -9.99E-03 | 9.99E-03 |
| Lin_1 | 950 | -70.008 | -103.194 | 10 | 3 | 9.99 | 3.01 |
| Split2_1 | 950 | -73.018 | -105.992 | -3.01 | 3.01 | 6.98 | 3.222 |
|
BasicMixer_1 |
0 | -67.039 | -99.425 | 5.979 | 4 | 12.959 | 3.81 |
| LPF1 | 0 | -67.04 | -99.425 | -8.23E-04 | 1.00E-02 | 12.958 | 3.81 |
| Lin_2 | 0 | -57.036 | -83.078 | 9.995 | 25 | 22.953 | 10.163 |
| LPF2 | 0 | -57.038 | -83.08 |
-1.90E-03 |
1.00E-02 | 22.951 | 10.163 |
在表5中,我们显示了使用传统弗里斯公式计算级联噪声系数的结果。与显示模拟器结果的表 4 的主要区别在于最后一列 CNF。
| 部件 |
F (分贝) |
增益(分贝) | CG (分贝) | 碳氢氟 (分贝) |
| 低频滤波器 | 0.01 | -0.01 | -0.01 | 0.01 |
| LNA | 3 | 10 | 9.99 | 3.01 |
| 分配器 | 3.01 | -3.01 | 6.98 | 3.22 |
| 搅拌机 | 4 | 5.979 | 12.96 | 3.81 |
| LPF1 | 0.01 | -0.01 | 12.95 | 3.81 |
| VGA | 25 | 9.995 | 22.94 | 12.65 |
| LPF2 | 0.01 | -0.01 | 22.93 | 12.65 |
显然,级联噪音数字出了问题。我们使用电子表格估计12.64dB,但模拟器发现10.16dB。级联增益匹配得相当好,但我们需要确定哪个噪声数据是有效的。首先,我们对整个结构的DSB噪声系数感兴趣,因为整个ZIF结构在两个边带中使用信号,并且在两个边带中都受到噪声的影响。因此,有必要得出涉及放大器的级联的DSB噪声系数,然后是混频器,然后是附加放大器(图11)。
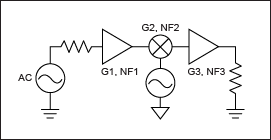
图 11.级联,包括混音器。
输出端的总噪声密度可计算为:
NOUT = 2kT0G1G2G3 + 2NA1G2G3 + NA2G3 + NA3
由级联输入端的热噪声引起的输出端噪声为:
NOT = 2kT0G1G2G3
这意味着整体噪声因子为:
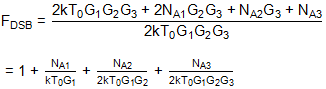
代:
F1 = 1 + NA1/(kT0G1), F2DSB = 1 + NA2/(2kT0G2), and F3 = 1 + NA3/(kT0G3)
收益 率:
FDSB = F1 + (F2DSB - 1)/G1 + (F3 - 1)/(2G1G2)
该推导表明,有必要在级联方程中使用混频器的DSB噪声系数,并且对于级联噪声系数,所有后续阶段的噪声贡献必须除以2,相对于弗里斯方程的通常形式。未能执行后一除以 2 会导致表 5 中所示的电子表格方程分析出错。在混频器之后修改电子表格单元格中的方程式以包括必要的除以2,得到的结果如表6所示。
| 部件 | F (分贝 | 增益(分贝) | CG (分贝) | 碳氢氟 (分贝) |
| 低频滤波器 | 0.01 | -0.01 | -0.01 | 0.01 |
| 液化天然气 | 3 | 10 | 9.99 | 3.01 |
| 分配器 | 3.01 | -3.01 | 6.98 | 3.22 |
| 搅拌机 | 4 | 5.979 | 12.96 | 3.81 |
| LPF1 | 0.01 | -0.01 | 12.95 | 3.81 |
| VGA | 25 | 9.995 | 22.94 | 10.17 |
| LPF2 | 0.01 | -0.01 | 22.93 | 10.17 |
表4和表6之间的一致性现在很好。然而,这个练习也证明了直接代入涉及混频器的弗里斯级联方程的危险。
接下来,我们考虑相同的情况,但所需信号比LO高300kHz。框图如图10所示,但所有信号都落在LO的高端。这使其成为相同接收器架构的低中频(LIF)应用。使用与以前相同的 Genesys 仿真工作区,结果如下表 7 所示。
| 部件 | CF (兆赫) | CP (分贝) | 压缩液 (分贝) | 增益(分贝) | 信噪比 (分贝) | CG (分贝) | 碳氢氟 (分贝) |
| MultiSource_1 | 950.3 | -79.999 | -116.194 | 0 | 0 | 0 | 0 |
| FE_BPF | 950.3 | -80.009 | -116.194 | -9.99E-03 | 1.00E-02 | -9.99E-03 | 9.99E-03 |
| Lin_1 | 950 | -70.008 | -103.194 | 10 | 3 | 9.99 | 3.01 |
| Split2_1 | 950 | -73.018 | -105.992 | -3.01 | 3.01 | 6.98 | 3.222 |
|
BasicMixer_1 |
0 | -67.039 | -99.425 | 5.979 | 4 | 12.959 | 3.81 |
| LPF1 | 0 | -67.04 | -99.425 | -8.23E-04 | 1.00E-02 | 12.958 | 3.81 |
| Lin_2 | 0 | -57.036 | -83.078 | 9.995 | 25 | 22.953 | 10.163 |
| LPF2 | 0 | -57.038 | -83.08 |
-1.90E-03 |
1.00E-02 | 22.951 | 10.163 |
这些结果与之前对相同架构的仿真相似,只是噪声系数增加了3dB。事实上,即使该系统的所有组件都是无噪声的,除了源电阻外,噪声系数也将为3dB。从本质上讲,这是复杂接收器结构的SSB应用,并且没有抑制不需要的边带的措施。级联噪声系数的推导与已经给出的相同,只是级联输入端热噪声引起的输出噪声再次为:
NOT = kT0G1G2G3
所以现在:
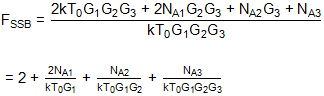
代:
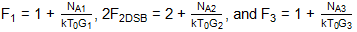
收益 率:
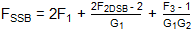
正如预期的那样,噪声级联方程中的每个项都乘以2,相对于这种结构的DSB用例。但是,这种情况有些人为。我们现在有一个接收器,在噪声和干扰方面对两个边带都敞开,但它仅用于其中一个边带中的信号。由于较低的边带只会增加接收器的脆弱性,因此使用正交通道为不需要的边带提供抑制是有意义的。一种解决方案是将接收器输出端的I和Q信号与90度合路器相结合,从而消除不需要的边带中的信号,同时建设性地将它们添加到所需的边带中。这实际上会将整个接收器转换为镜像抑制下变频器。最终组合级将系统噪声系数恢复先前损失的3dB,假设被组合信号的相位在组合点得到足够好的控制。这种方案的仿真原理图如图12所示,相应的结果如表8所示。
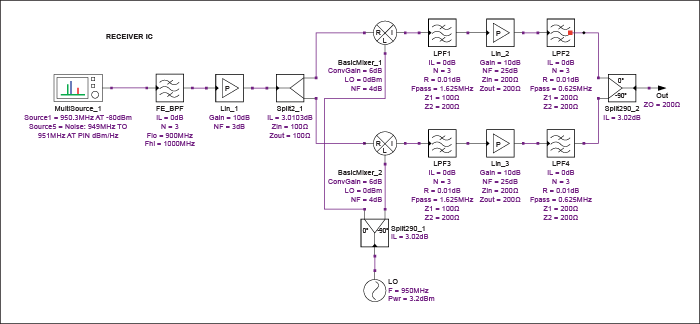
图 12.靠近具有镜像抑制功能的ZIF接收器。
| 部件 | CF (兆赫) | CP (分贝) | 压缩液 (分贝) | 增益(分贝) | 信噪比 (分贝) | CG (分贝) | 碳氢氟 (分贝) |
| MultiSource_1 | 950.3 | -79.995 | -116.194 | 0 | 0 | 0 | 0 |
| FE_BPF | 950.3 | -80.005 | -116.194 | -9.99E-03 | 1.00E-02 | -9.99E-03 | 9.99E-03 |
| Lin_1 | 950.3 | -70.004 | -103.194 | 10 | 3 | 9.99 | 3.01 |
| Split2_1 | 950.3 | -73.014 | -105.992 | -3.01 | 3.01 | 6.98 | 3.222 |
|
BasicMixer_1 |
0.3 | -67.053 | -96.441 | 5.958 | 4 | 12.938 | 6.815 |
| LPF1 | 0.3 | -67.005 | -96.443 | -1.64E-03 | 1.00E-02 | 12.936 | 6.815 |
| Lin_2 | 0.3 | -57.047 | -80.09 | 9.991 | 25 | 22.927 | 13.177 |
| LPF2 | 0.3 | -57.051 | -80.094 |
-3.82E-03 |
1.00E-02 | 22.923 | 13.177 |
| Split290_2 | 0.3 | -54.062 | -80.145 | 3.001 | 3.02 | 25.923 | 10.125 |
在最后(组合)阶段,级联噪声系数(CNF)提高了3dB,表明噪声系数如预期的那样恢复了。
事实证明,使用安捷伦 Genesys 模拟这些架构和场景与所研究案例中适当级联噪声系数的数学推导一致。®
对于讨论和仿真的每个架构,表9总结了级联噪声因数方程。
| 结构 | 应用 | 级联 F 方程 |
| 三个增益模块 | 任何 |
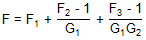 |
| 外差混频器 | SSB,理想的图像滤波 |

| 复杂下变频器 | 齐夫 |
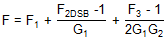 |
| 复杂下变频器 | LIF,无图像抑制 |
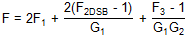 |
| 复杂下变频器 | LIF,图像拒绝组合 |
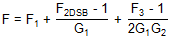 |
噪音温度
为了讨论Y因子噪声测量,有必要介绍噪声温度的概念。在之前的方程中,我们使用了众所周知的结果,即在给定温度下,电阻器可获得的噪声功率谱密度为kT,W/Hz,其中k是玻尔兹曼常数,T是绝对温度。如果我们假装器件无噪声,并且如果额外的噪声功率频谱密度由输入端接的噪声温度等效升高高于参考温度来解释,则可以解释设备中的所有噪声源。噪声因子可能与等效温度T有关e,通过 F = 1 + Te/T0,其中 T0定义为290K的参考噪声温度。不出所料,噪声因数 1 由器件的等效噪声温度 0K 表示,而噪声因数 2 由 T 表示e= 290K。
Y 因子
用于噪声系数测量的Y因子方法5涉及使用校准的噪声源,该噪声源具有两种不同的噪声温度,具体取决于设备是否存在直流电源。校准源具有特征性的超噪比(ENR),定义为:
ENRdB = 10log10 [(TSON - TSOFF)/T0]
其中 TS上是源在其ON状态下的噪声温度,T是S关闭是处于 OFF 状态的相应值。Y因子是两个噪声功率电平的比值,一个在噪声源打开时测量,另一个在噪声源关闭时测量。
Y = NON/NOFF
由于源的噪声功率可以直接用其噪声温度表示,因此我们也可以这样写:
Y = TON/TOFF
噪声因子测量和计算
为了评估DUT的噪声因数,我们必须将噪声功率测量设备连接到DUT的输出。让 DUT 具有噪声温度 T1且仪器的噪声温度T2.虽然不可能消除测量设备的噪声温度(T2) 从任何给定的读数中,我们可以测量 T12,这是 DUT 后跟仪器的综合噪声温度。我们可以使用计算来隔离 T1自 T 以来12= T1+ T2/G1.因此,策略是使用直接连接到测量仪器的校准噪声源进行Y因子测量,这将允许T2待定。我们有:
Y2 = N2ON/N2OFF = (TSON + T2)/(TSOFF + T2)
可以重新排列为:
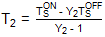
根据已知的T值获得测量装置的噪声温度S上和 TS关闭,下一步是测量 DUT 和测量仪器级联的新 Y 因子:
Y12 = N12ON/N12OFF
这允许使用与以前相同的程序计算 DUT 和仪器的组合噪声温度:
T12 = (TSON - Y12 TSOFF)/(Y12 - 1)
之前存储了两个 N1上和 N1关闭现在可以访问 N12上和 N12关闭,我们有足够的信息来计算 DUT 的增益,如下所示:
G1= (N12ON - N12OFF)/(N2ON - N2OFF)
这提供了足够的信息,可以使用以下方法在数学上减去测量仪器噪声温度的贡献:
T1 = T12 - T2/G1
被测器之前的损失
如果在DUT之前存在已知损耗,则必须消除这些损耗的影响,以获得DUT在其输入T处的真实噪声温度1在.假设这些损失是吸收性的,可以使用以下等式:
T1IN = (T1/LIN) - ((LIN - 1)TL/LIN)
其中 TL是物理温度的损耗和L在是要补偿的插入损耗,表示为大于单位的线性功率比。
混频器作为 DUT 在 Y 因子噪声因子测定中
考虑到用于噪声系数测量的校准噪声源本质上是宽带的,并且ON时噪声温度的任何微小变化都由嵌入在源中的详细校准表处理。因此,任何未经修改的Y因子技术使用都会导致对混频器的DSB噪声系数的评估。这是因为校准后的噪声源同时在两个边带中注入噪声功率,并且两个边带的组合输出噪声功率有助于用于计算Y因子的输出噪声温度。下面给出的两个示例案例说明了如何在修改和不修改的情况下使用测量方法分别获得DSB或SSB测量值。
通过Y因子法测量DSB噪声系数的示例
为了说明所讨论的概念,安捷伦 Genesys 仿真是通过向仿真的 DUT 中注入噪声源来执行的,该 DUT 是一个混频器,DSB 噪声系数为 4.9dB,转换增益为 8.8dB。注入的噪声功率由变量PIN决定,PIN是一个扫描变量,迭代两个可能的值-159dBm/Hz和-174dBm/Hz,分别代表噪声源的ON和OFF条件。IF定义为250MHz,混频器的RF端口的所需和镜像响应分别为2000MHz和1500MHz(图13)。仿真收集的唯一数据(表10和表11)是输入(直接连接到噪声源代替校准步骤)和输出(代表测量模式)在100kHz带宽内的通道噪声功率。
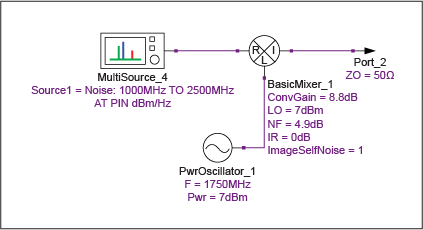
图 13.使用Y因子方法确定DSB混频器噪声系数的仿真原理图。
| B (赫兹) | IL (分贝)* | 引脚关闭 (分贝) | 引脚开启 (分贝) | 噘嘴关闭 (分贝) | 噘嘴 (分贝) |
| 100,000 | 0 | -123.975 | -109 | -107.265 | -96.91 |
| *请注意,参数IL表示DUT之前的插入损耗,在本例中为0dB。 | |||||
| Y2 | Y12 | T12(九) | T2(九) | T1(九) | T1在(九) | F (分贝) | 克 (分贝) |
| 31.443 | 10.851 | 606.147 | 0 | 606.147 | 606.147 | 4.9 | 8.8 |
请注意,T2表示仪器的噪声温度,这是可以接受的,因为在这种情况下,仪器是 Genesys 模拟器,它评估噪声而不添加任何自己的噪声。由于DUT之前的插入损耗为0dB,因此T1与 T 相同1在.Y因子测量的最终计算噪声系数由F = 10log给出10(1 + 吨1在/290).获得的值(4.9dB)与设置混频器原理图时使用的参数设置的预期值一致。
通过Y因子法测量SSB噪声系数的示例
仿真原理图如图14所示,测试结果如表12和表13所示。
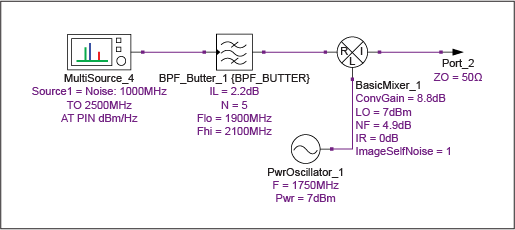
图 14.使用Y因子方法确定SSB混频器噪声系数的仿真原理图。
| B (赫兹) | IL (分贝)* | 引脚关闭 (分贝) | 引脚开启 (分贝) | 噘嘴关闭 (分贝) | 噘嘴 (分贝) |
| 100,000 | 2.2 | -123.975 | -109 | -108.015 | -101.455 |
| *请注意,参数IL表示DUT之前的插入损耗,在本例中为2.2dB。 | |||||
| Y2 | Y12 | T12(九) | T2(九) | T1(九) | T1在(九) | F (分贝) | 克 (分贝) |
| 31.443 | 4.529 | 2211.584 | 0 | 2211.584 | 1217.354 | 7.158 | 6.602 |
由于DUT之前的插入损耗为2.2dB,因此T1高于混频器的噪声温度T1在,已根据 DUT 前损耗部分中的公式 42 计算得出。Y因子测量的最终计算噪声系数由F = 10log给出10(1 + 吨1在/290).得到的值为7.158dB。该值应与公式43获得的值进行比较,假设光源的镜像噪声被完全抑制:
NF = 10log10(2(10(4.9/10)- 1) + 1) = 7.144dB
由于滤波器具有有限的插入损耗,因此镜像抑制滤波器在镜像频率下的阻抗并非完全无功。这反过来意味着源的像带噪声没有完全抑制,这被认为是理想噪声系数小幅增加的原因。
使用填充Y因子法测量SSB噪声系数的示例
在这种方法中,我们应用衰减器来确保混频器在所需频率和镜像频率下都受到类似的“冷”(即关断状态)噪声温度的影响。这应该导致SSB噪声系数更接近于比DSB噪声系数高3dB的值,因为源端接的噪声温度不再受到滤波器的任何显着影响(图15,表14和15)。
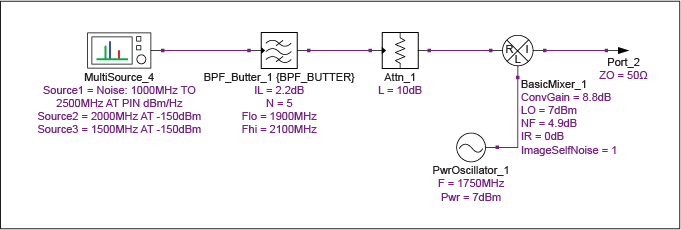
图 15.使用填充Y因子方法确定SSB混频器噪声系数的仿真原理图。
| B (赫兹) | IL (分贝)* | 引脚关闭 (分贝) | 引脚开启 (分贝) | 噘嘴关闭 (分贝) | 噘嘴 (分贝) |
| 100,000 | 12.2 | -123.975 | -109 | -107.272 | -106.141 |
| *请注意,参数IL表示DUT之前的插入损耗,在本例中为12.2dB,表示滤波器和衰减器的总损耗。 | |||||
| Y2 | Y12 | T12(九) | T2(九) | T1(九) | T1在(九) | F (分贝) | 克 (分贝) |
| 31.443 | 1.297 | 29392.313 | -5.98E-14 | 29392.313 | 1498.536 | 7.901 | -3.398 |
Y因子测量的最终计算噪声系数由F = 10log给出10(1 + 吨1在/290).得到的值为7.901dB。该值与在3.0dB的DSB噪声系数上增加4.9dB的预期值非常吻合。请注意,使用 10dB 衰减器会导致 Y 因子接近单位,这可能会危及精度。在实际测量中使用高衰减值时,建议选择可用的最高ENR源以保持精度。
结论
在本教程中,我们看到,当混频器是接收器级联的一部分时,级联噪声因子的弗里斯方程通常使用DSB或SSB版本的混频器噪声系数都无效。在使用滤波器在很大程度上消除接收器的镜像响应的情况下,可以用等效的双端口网络代替混频器、滤波器和LO子系统。但是,产生的噪声系数必须根据DSB噪声系数计算,同时考虑耦合到混频器输入端口的源端接的频率选择性。
我们还发现,相同的物理结构可能具有不同的有效噪声系数,这取决于信号是分布在LO周围还是完全分布在LO的一侧(即,应用分别是DSB或SSB)。在LIF模式下使用复数接收器引起的3dB信噪比损耗可以通过适当使用镜像抑制组合、复数滤波或等效基带处理来恢复。
Y因子测量评估混频器的DSB噪声系数,除非采取特殊措施来滤除镜像频率处的宽带噪声激励。这是用于先前推导的级联方程的适当值。当使用滤波器试图获得SSB噪声系数时,有必要考虑所用滤波器的插入损耗。此外,滤波器的源端接镜像噪声抑制程度可能导致偏离SSB噪声系数的经典定义。使用匹配衰减器可以在很大程度上克服这个问题,前提是使用的衰减量与噪声源的ENR相比不会过大。
审核编辑:郭婷
-
接收器
+关注
关注
14文章
2474浏览量
72016 -
混频器
+关注
关注
10文章
681浏览量
45751 -
无线电
+关注
关注
60文章
2145浏览量
116613
发布评论请先 登录
相关推荐
ADC噪声系数参数在数据转换器中有哪些应用?
软件无线电接收机的多速率处理技术研究
现代无线电接收机的系统噪声系数分析一:级联接收机的计算
现代无线电接收机的系统噪声系数分析二:Y因子噪声因子测量法
怎么样使用PCI总线实现软件无线电接收机系统的设计资料说明
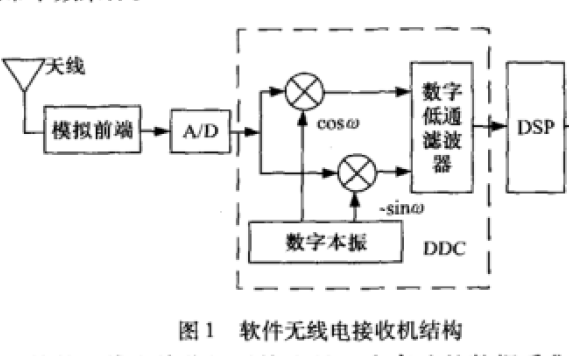
基于专用DDC的软件无线电接收机的设计





 现代无线电接收机的系统噪声系数分析
现代无线电接收机的系统噪声系数分析












评论